Difference between revisions of "Aufgaben:Exercise 3.8: Once more Mutual Information"
| (9 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Different_Entropy_Measures_of_Two-Dimensional_Random_Variables |
}} | }} | ||
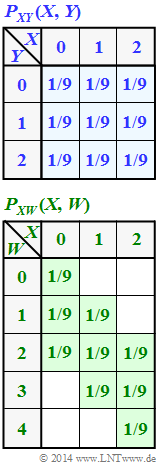
| − | [[File:P_ID2768__Inf_A_3_7_neu.png|right|frame| | + | [[File:P_ID2768__Inf_A_3_7_neu.png|right|frame|2D–Functions <br> $P_{ XY }$ und $P_{ XW }$]] |
| − | + | We consider the tuple $Z = (X, Y)$, where the individual components $X$ and $Y$ each represent ternary random variables: | |
:$$X = \{ 0 ,\ 1 ,\ 2 \} , \hspace{0.3cm}Y= \{ 0 ,\ 1 ,\ 2 \}.$$ | :$$X = \{ 0 ,\ 1 ,\ 2 \} , \hspace{0.3cm}Y= \{ 0 ,\ 1 ,\ 2 \}.$$ | ||
| − | + | The joint probability function $P_{ XY }(X, Y)$ of both random variables is given in the upper graph. | |
| − | In | + | In [[Aufgaben:Exercise_3.8Z:_Tuples_from_Ternary_Random_Variables|Exercise 3.8Z]] this constellation is analyzed in detail. One obtains as a result (all data in "bit"): |
:* $H(X) = H(Y) = \log_2 (3) = 1.585,$ | :* $H(X) = H(Y) = \log_2 (3) = 1.585,$ | ||
:* $H(XY) = \log_2 (9) = 3.170,$ | :* $H(XY) = \log_2 (9) = 3.170,$ | ||
| Line 16: | Line 16: | ||
:* $I(X, Z) = 1.585.$ | :* $I(X, Z) = 1.585.$ | ||
| − | + | Furthermore, we consider the random variable $W = \{ 0,\ 1,\ 2,\ 3,\ 4 \}$, whose properties result from the composite probability function $P_{ XW }(X, W)$ according to the sketch below. The probabilities are zero in all fields with a white background. | |
| − | + | What is sought in the present exercise is the mutual information between | |
| − | :* | + | :*the random variables $X$ and $W$ ⇒ $I(X; W)$, |
| − | :* | + | :*the random variables $Z$ and $W ⇒ I(Z; W)$. |
| Line 26: | Line 26: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Information_Theory/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen|Different entropies of two-dimensional random variables]]. |
| − | * | + | *In particular, reference is made to the sections <br> [[Information_Theory/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Conditional_probability_and_conditional_entropy|Conditional probability and conditional entropy]] as well as <br> [[Information_Theory/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Mutual_information_between_two_random_variables|Mutual information between two random variables]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {How might the variables $X$, $Y$ and $W$ be related? |
|type="[]"} | |type="[]"} | ||
+ $W = X + Y$, | + $W = X + Y$, | ||
| Line 41: | Line 41: | ||
-$W = Y - X + 2$. | -$W = Y - X + 2$. | ||
| − | { | + | {What is the mutual information between the random variables $X$ and $W$? |
|type="{}"} | |type="{}"} | ||
$I(X; W) \ = \ $ { 0.612 3% } $\ \rm bit$ | $I(X; W) \ = \ $ { 0.612 3% } $\ \rm bit$ | ||
| − | { | + | {What is the mutual information between the random variables $Z$ and $W$? |
|type="{}"} | |type="{}"} | ||
$I(Z; W) \ = \ $ { 2.197 3% } $\ \rm bit$ | $I(Z; W) \ = \ $ { 2.197 3% } $\ \rm bit$ | ||
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $H(ZW) = H(XW)$ is true. |
| − | + | + | + $H(W|Z) = 0$ is true. |
| − | + | + | + $I(Z; W) > I(X; W)$ is true. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The <u>correct solutions are 1 and 2</u>: |
| − | * | + | *With $X = \{0,\ 1,\ 2\}$, $Y = \{0,\ 1,\ 2\}$ , $X + Y = \{0,\ 1,\ 2,\ 3,\ 4\}$ holds. |
| − | * | + | *The probabilities also agree with the given probability function. |
| − | * | + | *Checking the other two specifications shows that $W = X - Y + 2$ is also possible, but not $W = Y - X + 2$. |
| + | [[File:P_ID2769__Inf_A_3_7d.png|right|frame|To calculate the mutual information]] | ||
| − | '''(2)''' | + | |
| − | * | + | '''(2)''' From the two-dimensional probability mass function $P_{ XW }(X, W)$ in the specification section, one obtains for |
| + | *the joint entropy: | ||
:$$H(XW) = {\rm log}_2 \hspace{0.1cm} (9) | :$$H(XW) = {\rm log}_2 \hspace{0.1cm} (9) | ||
= 3.170\ {\rm (bit)} | = 3.170\ {\rm (bit)} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * | + | * the probability function of the random variable $W$: |
:$$P_W(W) = \big [\hspace{0.05cm}1/9\hspace{0.05cm}, \hspace{0.15cm} 2/9\hspace{0.05cm},\hspace{0.15cm} 3/9 \hspace{0.05cm}, \hspace{0.15cm} 2/9\hspace{0.05cm}, \hspace{0.15cm} 1/9\hspace{0.05cm} \big ]\hspace{0.05cm},$$ | :$$P_W(W) = \big [\hspace{0.05cm}1/9\hspace{0.05cm}, \hspace{0.15cm} 2/9\hspace{0.05cm},\hspace{0.15cm} 3/9 \hspace{0.05cm}, \hspace{0.15cm} 2/9\hspace{0.05cm}, \hspace{0.15cm} 1/9\hspace{0.05cm} \big ]\hspace{0.05cm},$$ | ||
| − | * | + | *the entropy of the random variable $W$: |
:$$H(W) = 2 \cdot \frac{1}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{1} + 2 \cdot \frac{2}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{2} + | :$$H(W) = 2 \cdot \frac{1}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{1} + 2 \cdot \frac{2}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{2} + | ||
\frac{3}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{3} | \frac{3}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{3} | ||
{= 2.197\ {\rm (bit)}} \hspace{0.05cm}.$$ | {= 2.197\ {\rm (bit)}} \hspace{0.05cm}.$$ | ||
| − | + | Thus, with $H(X) = 1.585 \ \rm bit$ (was given), the result for the mutual information: | |
:$$I(X;W) = H(X) + H(W) - H(XW) = 1.585 + 2.197- 3.170\hspace{0.15cm} \underline {= 0.612\ {\rm (bit)}} \hspace{0.05cm}.$$ | :$$I(X;W) = H(X) + H(W) - H(XW) = 1.585 + 2.197- 3.170\hspace{0.15cm} \underline {= 0.612\ {\rm (bit)}} \hspace{0.05cm}.$$ | ||
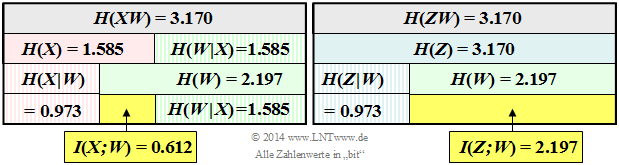
| − | + | The left of the two diagrams illustrates the calculation of the mutual information $I(X; W)$ between the first component $X$ and the sum $W$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:P_ID2770__Inf_A_3_7c.png|right|frame|Joint probability between $Z$ and $W$]] | |
| − | * | + | '''(3)''' The second graph shows the joint probability $P_{ ZW }(⋅)$. |
| − | * | + | *The scheme consists of $5 · 9 = 45$ fields in contrast to the plot of $P_{ XW }(⋅)$ in the data section with $3 · 9 = 27$ fields. |
| − | * | + | *However, of the $45$ fields, only nine are also assigned non-zero probabilities. The following applies to the joint entropy: $H(ZW) = 3.170\ {\rm (bit)} \hspace{0.05cm}.$ |
| − | * | + | *With the further entropies $H(Z) = 3.170\ {\rm (bit)}\hspace{0.05cm}$ and $H(W) = 2.197\ {\rm (bit)}\hspace{0.05cm}$ according to [[Aufgaben:Exercise_3.8Z:_Tuples_from_Ternary_Random_Variables| Exercise 3.8Z]] or the subquestion '''(2)''' of this exercise, one obtains for the mutual information: |
| − | * | + | :$$I(Z;W) = H(Z) + H(W) - H(ZW) \hspace{0.15cm} \underline {= 2.197\,{\rm (bit)}} \hspace{0.05cm}.$$ |
| + | <br clear=all> | ||
| + | '''(4)''' <u>All three statements</u> are true, as can also be seen from the right-hand side of the two upper diagrams. We attempt an interpretation of these numerical results: | ||
| + | * The joint probability $P_{ ZW }(⋅)$ is composed, like $P_{ XW }(⋅)$ , of nine equally probable elements unequal to 0. It is thus obvious that the joint entropies are also equal ⇒ $H(ZW) = H(XW) = 3.170 \ \rm (bit)$. | ||
| + | * If I know the tuple $Z = (X, Y)$, I naturally also know the sum $W = X + Y$. Thus $H(W|Z) = 0$. | ||
| + | *In contrast, $H(Z|W) \ne 0$. Rather, $H(Z|W) = H(X|W) = 0.973 \ \rm (bit)$. | ||
| + | *The random variable $W$ thus provides exactly the same information with regard to the tuple $Z$ as for the individual component $X$. This is the verbal interpretation of the statement $H(Z|W) = H(X|W)$. | ||
| + | *The joint information of $Z$ and $W$ ⇒ $I(Z; W)$ is greater than the joint information of $X$ and $W$ ⇒ $I(X; W)$, because $H(W|Z) =0$, while $H(W|X)$ is non-zero, namely exactly as great as $H(X)$ : | ||
:$$I(Z;W) = H(W) - H(W|Z) = 2.197 - 0= 2.197\,{\rm (bit)} \hspace{0.05cm},$$ | :$$I(Z;W) = H(W) - H(W|Z) = 2.197 - 0= 2.197\,{\rm (bit)} \hspace{0.05cm},$$ | ||
:$$I(X;W) = H(W) - H(W|X) = 2.197 - 1.585= 0.612\,{\rm (bit)} \hspace{0.05cm}.$$ | :$$I(X;W) = H(W) - H(W|X) = 2.197 - 1.585= 0.612\,{\rm (bit)} \hspace{0.05cm}.$$ | ||
Latest revision as of 14:50, 17 November 2022
We consider the tuple $Z = (X, Y)$, where the individual components $X$ and $Y$ each represent ternary random variables:
- $$X = \{ 0 ,\ 1 ,\ 2 \} , \hspace{0.3cm}Y= \{ 0 ,\ 1 ,\ 2 \}.$$
The joint probability function $P_{ XY }(X, Y)$ of both random variables is given in the upper graph.
In Exercise 3.8Z this constellation is analyzed in detail. One obtains as a result (all data in "bit"):
- $H(X) = H(Y) = \log_2 (3) = 1.585,$
- $H(XY) = \log_2 (9) = 3.170,$
- $I(X, Y) = 0,$
- $H(Z) = H(XZ) = 3.170,$
- $I(X, Z) = 1.585.$
Furthermore, we consider the random variable $W = \{ 0,\ 1,\ 2,\ 3,\ 4 \}$, whose properties result from the composite probability function $P_{ XW }(X, W)$ according to the sketch below. The probabilities are zero in all fields with a white background.
What is sought in the present exercise is the mutual information between
- the random variables $X$ and $W$ ⇒ $I(X; W)$,
- the random variables $Z$ and $W ⇒ I(Z; W)$.
Hints:
- The exercise belongs to the chapter Different entropies of two-dimensional random variables.
- In particular, reference is made to the sections
Conditional probability and conditional entropy as well as
Mutual information between two random variables.
Questions
Solution
- With $X = \{0,\ 1,\ 2\}$, $Y = \{0,\ 1,\ 2\}$ , $X + Y = \{0,\ 1,\ 2,\ 3,\ 4\}$ holds.
- The probabilities also agree with the given probability function.
- Checking the other two specifications shows that $W = X - Y + 2$ is also possible, but not $W = Y - X + 2$.
(2) From the two-dimensional probability mass function $P_{ XW }(X, W)$ in the specification section, one obtains for
- the joint entropy:
- $$H(XW) = {\rm log}_2 \hspace{0.1cm} (9) = 3.170\ {\rm (bit)} \hspace{0.05cm},$$
- the probability function of the random variable $W$:
- $$P_W(W) = \big [\hspace{0.05cm}1/9\hspace{0.05cm}, \hspace{0.15cm} 2/9\hspace{0.05cm},\hspace{0.15cm} 3/9 \hspace{0.05cm}, \hspace{0.15cm} 2/9\hspace{0.05cm}, \hspace{0.15cm} 1/9\hspace{0.05cm} \big ]\hspace{0.05cm},$$
- the entropy of the random variable $W$:
- $$H(W) = 2 \cdot \frac{1}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{1} + 2 \cdot \frac{2}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{2} + \frac{3}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{3} {= 2.197\ {\rm (bit)}} \hspace{0.05cm}.$$
Thus, with $H(X) = 1.585 \ \rm bit$ (was given), the result for the mutual information:
- $$I(X;W) = H(X) + H(W) - H(XW) = 1.585 + 2.197- 3.170\hspace{0.15cm} \underline {= 0.612\ {\rm (bit)}} \hspace{0.05cm}.$$
The left of the two diagrams illustrates the calculation of the mutual information $I(X; W)$ between the first component $X$ and the sum $W$.
(3) The second graph shows the joint probability $P_{ ZW }(⋅)$.
- The scheme consists of $5 · 9 = 45$ fields in contrast to the plot of $P_{ XW }(⋅)$ in the data section with $3 · 9 = 27$ fields.
- However, of the $45$ fields, only nine are also assigned non-zero probabilities. The following applies to the joint entropy: $H(ZW) = 3.170\ {\rm (bit)} \hspace{0.05cm}.$
- With the further entropies $H(Z) = 3.170\ {\rm (bit)}\hspace{0.05cm}$ and $H(W) = 2.197\ {\rm (bit)}\hspace{0.05cm}$ according to Exercise 3.8Z or the subquestion (2) of this exercise, one obtains for the mutual information:
- $$I(Z;W) = H(Z) + H(W) - H(ZW) \hspace{0.15cm} \underline {= 2.197\,{\rm (bit)}} \hspace{0.05cm}.$$
(4) All three statements are true, as can also be seen from the right-hand side of the two upper diagrams. We attempt an interpretation of these numerical results:
- The joint probability $P_{ ZW }(⋅)$ is composed, like $P_{ XW }(⋅)$ , of nine equally probable elements unequal to 0. It is thus obvious that the joint entropies are also equal ⇒ $H(ZW) = H(XW) = 3.170 \ \rm (bit)$.
- If I know the tuple $Z = (X, Y)$, I naturally also know the sum $W = X + Y$. Thus $H(W|Z) = 0$.
- In contrast, $H(Z|W) \ne 0$. Rather, $H(Z|W) = H(X|W) = 0.973 \ \rm (bit)$.
- The random variable $W$ thus provides exactly the same information with regard to the tuple $Z$ as for the individual component $X$. This is the verbal interpretation of the statement $H(Z|W) = H(X|W)$.
- The joint information of $Z$ and $W$ ⇒ $I(Z; W)$ is greater than the joint information of $X$ and $W$ ⇒ $I(X; W)$, because $H(W|Z) =0$, while $H(W|X)$ is non-zero, namely exactly as great as $H(X)$ :
- $$I(Z;W) = H(W) - H(W|Z) = 2.197 - 0= 2.197\,{\rm (bit)} \hspace{0.05cm},$$
- $$I(X;W) = H(W) - H(W|X) = 2.197 - 1.585= 0.612\,{\rm (bit)} \hspace{0.05cm}.$$