Exercise 4.06: Optimal Decision Boundaries
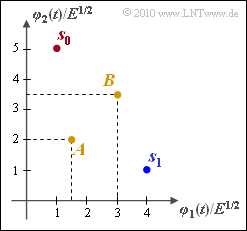
We consider a binary message system $(M = 2)$ that is defined by the drawn 2D signal space constellation $(N = 2)$. The following applies to the two possible transmitted vectors that are directly coupled to the messages $m_0$ and $m_1$:
- $$\boldsymbol{ s }_0 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (1,\hspace{0.1cm} 5) \hspace{0.2cm} \Leftrightarrow \hspace{0.2cm} m_0 \hspace{0.05cm},$$
- $$ \boldsymbol{ s }_1 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (4, \hspace{0.1cm}1) \hspace{0.2cm} \Leftrightarrow \hspace{0.2cm} m_1 \hspace{0.05cm}.$$
The optimal decision boundary between the regions $I_0 ⇔ m_0$ and $I_1 ⇔ m_1$ is sought, whereby the following assumptions are made:
- The following applies to subtasks (1) to (3)
- $${\rm Pr}(m_0 ) = {\rm Pr}(m_1 ) = 0.5 \hspace{0.05cm}. $$
- For subtasks (4) and (5), on the other hand, the following should apply:
- $${\rm Pr}(m_0 ) = 0.817 \hspace{0.05cm},\hspace{0.2cm} {\rm Pr}(m_1 ) = 0.183\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = 1.5 \hspace{0.05cm}.$$
For AWGN noise with variance $\sigma_n^2$, the decision limit is the solution of the following vectorial equation with respect to the vector $(\rho_1, \rho_2)$:
- $$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 + 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{ \rho } = (\rho_1 , \hspace{0.1cm}\rho_2 )\hspace{0.05cm}.$$
In addition, two received values
- $$\boldsymbol{ A }= \sqrt {E} \cdot (1.5, \hspace{0.1cm}2)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ B }= \sqrt {E} \cdot (3, \hspace{0.1cm}3.5) $$
are drawn in the graphic. It must be checked whether these should be assigned to the regions $I_0$ $($and thus the message $m_0)$ or $I_1$ $($message $m_1)$ given the corresponding boundary conditions.
Notes:
- The exercise belongs to the chapter "Approximation of the Error Probability".
- For numeric calculations, the energy $E = 1$ can be set for simplification.
Questions
Solution
- $$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$
With the given vector values, i.e. the numerical values
- $$|| \boldsymbol{ s }_1||^2 = 4^2 + 1^2 = 17\hspace{0.05cm}, \hspace{0.2cm} || \boldsymbol{ s }_0||^2 = 1^2 + 5^2 = 26\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_1 - \boldsymbol{ s }_0 = (3,\hspace{0.1cm}-4) \hspace{0.05cm}$$
one obtains the following equation for the decision limits:
- $$3 \cdot \rho_1 - 4 \cdot \rho_2 = ({17-26})/{2} = - {9}/{2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\rho_2 = 3/4 \cdot \rho_1 + 9/8 \hspace{0.05cm}.$$
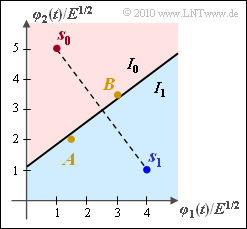
The decision limit lies in the middle between $s_0$ and $s_1$ and is rotated by $90^\circ$ compared to the connecting line between the two symbols. It goes through the point $(2.5, \ \, 3)$. So the first solution is correct.
Solution 2, on the other hand, describes the connecting line itself and $\rho_2 = 3$ is a horizontal line.
(2) The decision area $I_1$ should of course contain the point $s_1$ ⇒ area below the decision line. Point $A = (1.5, \ \, 2)$ belongs to this decision domain, as shown in the graphic. This can be shown mathematically, since the decision line goes through the point $(1.5, \ \, 2.25)$, for example, and thus $(1.5, \ \, 2)$ lies below the decision line. So solution 2 is correct.
(3) The decision line also goes through the point $(3, \ \, 3.375)$. $B = (3, \ \, 3.5)$ lies above and therefore belongs to the decision region $I_0$ according to solution 1.
(4) According to the equation in the information section and the calculations for subtask (1), the following now applies:
- $$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 + 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$
With $|| \boldsymbol{ s }_1||^2 = 17$, $|| \boldsymbol{ s }_0||^2 = 26$, $ \boldsymbol{ s }_1 \, –\boldsymbol{ s }_0 = (3, \ \, –4)$ we obtain:
- $$\rho_2 = 3/4 \cdot \rho_1 + 9/8 - K /8 \hspace{0.05cm}.$$
The following abbreviation was used here:
- $$K = 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = 2 \cdot 1^2 \cdot 1.5 = 3 \hspace{0.05cm}.$$
From this it follows:
- $$\rho_2 = 3/4 \cdot \rho_1 + 9/8 - 3 /8 = 3/4 \cdot \rho_1 + 3/4 \hspace{0.05cm}.$$
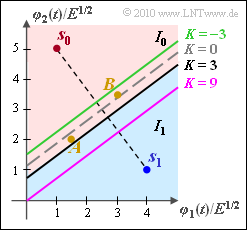
The decision line is shifted down by $3/8$ (black curve, labeled "$K = 3$" in the graphic). So solution 2 is correct.
- The first equation describes the optimal decision boundary for equally probable symbols ($K = 0$, dashed gray).
- The third equation is valid for $K = \, –3$. This results with $\sigma_n^2 = 1$ for the symbol probabilities ${\rm Pr}(m_1) \approx 0.817$ and ${\rm Pr}(m_0) \approx 0.138$ (green curve).
- The violet straight line results with $K = 9$, i.e. with the same probabilities as for the black curve, but now with the variance $\sigma_n^2 = 3$.
(5) The graphic above already shows that both $A$ and $B$ now belong to the decision regio $I_0$. Solutions 1 and 3 are correct.