Difference between revisions of "Aufgaben:Exercise 4.09Z: Laplace Distributed Noise"
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digital_Signal_Transmission/Approximation_of_the_Error_Probability}} | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Approximation_of_the_Error_Probability}} | ||
| − | [[File:P_ID2042__Dig_Z_4_9.png|right|frame| | + | [[File:P_ID2042__Dig_Z_4_9.png|right|frame|Two-dimensional Laplacian PDF]] |
We consider two-dimensional noise $\boldsymbol{n} = (n_1, n_2)$. | We consider two-dimensional noise $\boldsymbol{n} = (n_1, n_2)$. | ||
| − | The two noise variables are " | + | The two noise variables are "independent and identically distributed", abbreviated "i.i.d.", and each has a Laplace probability density function $\rm (PDF)$: |
:$$p_{n_1}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |x|} \hspace{0.05cm},$$ | :$$p_{n_1}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |x|} \hspace{0.05cm},$$ | ||
:$$ p_{n_2}(y) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |y|} \hspace{0.05cm}. $$ | :$$ p_{n_2}(y) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |y|} \hspace{0.05cm}. $$ | ||
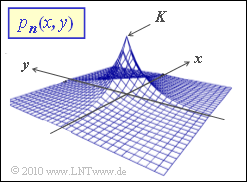
| − | *The | + | *The two-dimensional probability density function $p_{\it \boldsymbol{n}}(x, y)$ is shown in the graph. |
| − | |||
| + | *To simplify notation, the realizations of $n_1$ and $n_2$ are denoted here by $x$ and $y$, respectively. | ||
| − | + | ||
| − | * The exercise belongs to the chapter [[Digital_Signal_Transmission/Approximation_of_the_Error_Probability|"Approximation of the Error Probability"]]. | + | Notes: |
| − | * We would like to refer to the interactive applet [[Applets:2D_Laplace|"2D Laplace"]]. | + | * The exercise belongs to the chapter [[Digital_Signal_Transmission/Approximation_of_the_Error_Probability|"Approximation of the Error Probability"]]. |
| − | * The integral resulting in subtask '''(6)''' must be split into several partial integrals due to the magnitude formation. | + | |
| − | *Furthermore, it holds: | + | * We would like to refer to the (German language) interactive SWF applet [[Applets:2D_Laplace|"2D Laplace"]]. |
| − | + | ||
| + | * The integral resulting in subtask '''(6)''' must be split into several partial integrals due to the magnitude formation. | ||
| + | |||
| + | *Furthermore, it holds: $\int_{0}^{\infty} x^2 \cdot {\rm e}^{-a \hspace{0.03cm}\cdot \hspace{0.03cm} x} \,{\rm d} x = {2}/{a^3} \hspace{0.05cm}.$ | ||
| Line 25: | Line 28: | ||
===Questions=== | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What is the size of the constant $K$ of the | + | {What is the size of the constant $K$ of the one-dimensional PDF? |
|type="[]"} | |type="[]"} | ||
- $K = 1$. | - $K = 1$. | ||
| Line 31: | Line 34: | ||
- $K = 1/a$. | - $K = 1/a$. | ||
| − | {Let $a = 1$. What are the mean ${\rm E}\big[n_i \big]$ and variance $\sigma^2 = {\rm E}\big[n_i^2\big]$ of the two | + | {Let $a = 1$. What are the mean ${\rm E}\big[n_i \big]$ and the variance $\sigma^2 = {\rm E}\big[n_i^2\big]$ of the two one-dimensional random variables? $(i = 1,\ 2)$. |
|type="{}"} | |type="{}"} | ||
${\rm E}\big[n_i\big] \ = \ $ { 0. } | ${\rm E}\big[n_i\big] \ = \ $ { 0. } | ||
${\rm E}\big[n_i^2\big] \ = \ ${ 2 3% } | ${\rm E}\big[n_i^2\big] \ = \ ${ 2 3% } | ||
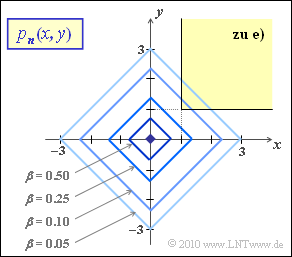
| − | {What is the shape of the contour lines of the | + | {What is the shape of the contour lines of the two-dimensional PDF in the first quadrant? |
| − | |type=" | + | |type="()"} |
+ They are straight lines. | + They are straight lines. | ||
- They are hyperbolas. | - They are hyperbolas. | ||
- They are circles. | - They are circles. | ||
| − | {Let further $a = 1$. What is the probability that both $n_1$ and $n_2$ are negative? | + | {Let further $a = 1$. What is the probability that both $n_1$ and $n_2$ are negative? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}\big[(n_1 < 0) ∩ (n_2 < 0)\big]\ = \ $ { 25 3% } $\ \%$ | ${\rm Pr}\big[(n_1 < 0) ∩ (n_2 < 0)\big]\ = \ $ { 25 3% } $\ \%$ | ||
| Line 50: | Line 53: | ||
${\rm Pr}\big[(n_1 > 1) ∩ (n_2 > 1)\big]\ = \ $ { 3.4 3% } $\ \%$ | ${\rm Pr}\big[(n_1 > 1) ∩ (n_2 > 1)\big]\ = \ $ { 3.4 3% } $\ \%$ | ||
| − | {What is the probability that the sum | + | {What is the probability that the sum $n_1 + n_2 > 2$? |
|type="{}"} | |type="{}"} | ||
$ {\rm Pr}\big[n_1 + n_2 > 2)\big] \ = \ $ { 13.5 3% } $\ \%$ | $ {\rm Pr}\big[n_1 + n_2 > 2)\big] \ = \ $ { 13.5 3% } $\ \%$ | ||
Revision as of 14:47, 30 July 2022
We consider two-dimensional noise $\boldsymbol{n} = (n_1, n_2)$.
The two noise variables are "independent and identically distributed", abbreviated "i.i.d.", and each has a Laplace probability density function $\rm (PDF)$:
- $$p_{n_1}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |x|} \hspace{0.05cm},$$
- $$ p_{n_2}(y) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} K \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm} |y|} \hspace{0.05cm}. $$
- The two-dimensional probability density function $p_{\it \boldsymbol{n}}(x, y)$ is shown in the graph.
- To simplify notation, the realizations of $n_1$ and $n_2$ are denoted here by $x$ and $y$, respectively.
Notes:
- The exercise belongs to the chapter "Approximation of the Error Probability".
- We would like to refer to the (German language) interactive SWF applet "2D Laplace".
- The integral resulting in subtask (6) must be split into several partial integrals due to the magnitude formation.
- Furthermore, it holds: $\int_{0}^{\infty} x^2 \cdot {\rm e}^{-a \hspace{0.03cm}\cdot \hspace{0.03cm} x} \,{\rm d} x = {2}/{a^3} \hspace{0.05cm}.$
Questions
Solution
- The area under the PDF must equal $1$:
- $$\int_{-\infty}^{+\infty} p_{n_1}(x) \,{\rm d} x = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \int_{0}^{+\infty} p_{n_1}(x) \,{\rm d} x = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K \cdot \int_{0}^{\infty} {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}x} \,{\rm d} x = - {K}/{a} \cdot \left [ {\rm e}^{- a \hspace{0.03cm} \cdot \hspace{0.03cm} x} \right ]_{0}^{\infty}= {K}/{a} = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K = {a}/{2}\hspace{0.05cm}.$$
(2) The linear mean is equal to 0 due to PDF symmetry.
Thus, the variance $\sigma^2$ is actually equal to the root mean square, as already stated in the question:
- $$\sigma^2 = {\rm E}[n_1^2] = 2 \cdot \frac{a}{2} \cdot \int_{0}^{\infty} x^2 \cdot {\rm e}^{-a \hspace{0.03cm} \cdot \hspace{0.03cm} x} \,{\rm d} x = a \cdot {2}/{a^3}= {2}/{a^2} \hspace{0.05cm}. \hspace{0.2cm}{\rm Mit}\hspace{0.15cm}a = 1\text{:} \hspace{0.2cm}\hspace{0.1cm}\underline {\sigma^2 = 2 }\hspace{0.05cm}.$$
(3) Solution 1 is correct:
- In the first quadrant ($x ≥ 0, y ≥ 0$), the magnitude formation can be omitted. Then the 2D PDF is given by:
- $$\boldsymbol{ p }_{\boldsymbol{ n }} (x,\hspace{0.15cm} y) = {a^2}/{4} \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}x} \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}y }= {a^2}/{4} \cdot {\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}(x+y)}\hspace{0.05cm}.$$
- A contour line with factor $\beta$ versus maximum then has the following shape ($0 < \beta < 1$):
- $${\rm e}^{- a \hspace{0.03cm}\cdot \hspace{0.03cm}(x+y)} = \beta \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x + y = \frac{{\rm ln}\hspace{0.15cm}1/\beta}{a} \hspace{0.05cm}.$$
- The graph shows the contour lines for $a = 1$ and some values of $\beta$, each giving a square rotated by $45^\circ$ ⇒ the contour lines are thus even.
(4) The probability event considered here corresponds exactly to the third quadrant of the composite PDF sketched above. Because of symmetry, this probability is:
- $${\rm Pr}[(n_1 < 0) ∩ (n_2 < 0)]\hspace{0.15cm}\underline {=25\%}.$$
(5) For this, the composite PDF can be written:
- $${\rm Pr} \left [ (n_1 > 1)\cap (n_2 > 1)\right ] = {1}/{4} \cdot \int_{1}^{\infty} \int_{1}^{\infty}{\rm e}^{- (x+y)} \,{\rm d} x \,{\rm d} y == {1}/{2} \cdot \int_{1}^{\infty} {\rm e}^{- x} \,{\rm d} x \hspace{0.15cm} \cdot \hspace{0.15cm} {1}/{2} \cdot \int_{1}^{\infty} {\rm e}^{- y} \,{\rm d} y $$
- $$ \Rightarrow \hspace{0.3cm}{\rm Pr} \left [ (n_1 > 1)\cap (n_2 > 1)\right ] = \left [ {\rm Pr} (n_1 > 1)\right ] \cdot \left [ {\rm Pr} (n_2 > 1)\right ]\hspace{0.05cm}. $$
Considered is the statistical independence between $n_1$ and $n_2$ and the equality $p_{\it n1}(x) = p_{\it n2}(y)$. For $a = 1$ holds:
- $${\rm Pr} (n_1 > 1) = {1}/{2} \cdot \int_{1}^{\infty} {\rm e}^{- x} \,{\rm d} x = {1}/({2{\rm e}})\approx 0.184\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr} \left [ (n_1 > 1)\cap (n_2 > 1)\right ] = {1}/({4{\rm e}^2)}\hspace{0.1cm}\hspace{0.15cm}\underline {\approx 3.4\%}\hspace{0.05cm}.$$
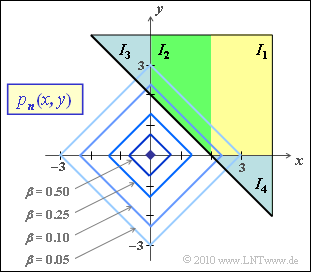
(6) The region considered here is highlighted in color in the following graph.
- However, the regions extend to the right and above to infinity.
- The searched probability results in
- $${\rm Pr} [ n_1 \hspace{-0.2cm} \ + \ \hspace{-0.2cm} n_2 > 2 ] =\frac{1}{4} \cdot \int\limits_{-\infty}^{+\infty} {\rm e}^{-|x|} \int\limits_{2-x}^{\infty}{\rm e}^{-|y|} \,{\rm d} y \,{\rm d} x = I_1 + I_2 + I_3 + I_4 \hspace{0.05cm}.$$
Because of the magnitude, a splitting into partial integrals has to be done. Upwards and to the right all areas extend to infinity. Because of the symmetry $I_4 = I_3$ is valid.
- $$I_1 = {1}/{4} \cdot \int_{2}^{+\infty} \hspace{-0.15cm}{\rm e}^{-x} \int_{0}^{\infty}\hspace{-0.15cm}{\rm e}^{-y} \,{\rm d} y \,{\rm d} x = {1}/{4} \cdot \int_{2}^{+\infty} {\rm e}^{-x} \,{\rm d} x ={1}/({4{\rm e}^2})\hspace{0.05cm},$$
- $$I_2 = {1}/{4} \cdot \hspace{-0.1cm} \int_{0}^{2} \hspace{-0.15cm}{\rm e}^{-x} \int_{2-x}^{\infty}\hspace{-0.15cm}{\rm e}^{-y} \,{\rm d} y \,{\rm d} x = {1}/{4} \cdot \hspace{-0.1cm} \int_{0}^{2} {\rm e}^{-x}\hspace{-0.1cm} \cdot {\rm e}^{x-2} \,{\rm d} x$$
- $$\Rightarrow \hspace{0.3cm}I_2 = {1}/{4} \cdot \hspace{-0.1cm}\int_{0}^{2} {\rm e}^{-2} \,{\rm d} x = {1}/({2{\rm e}^2})\hspace{0.05cm},$$
- $$I_3 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{x} \int_{2-x}^{\infty}{\rm e}^{-y} \,{\rm d} y \,{\rm d} x = {1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{x} \cdot {\rm e}^{x-2} \,{\rm d} x = {1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{2x-2} \,{\rm d} x = \frac{{\rm e}^{-2}}{4} \cdot \int_{0}^{\infty} {\rm e}^{-2x} \,{\rm d} x = {1}/({8{\rm e}^2})\hspace{0.05cm},$$
- $$I_4 ={1}/{4} \cdot \int_{-\infty}^{0} {\rm e}^{y} \int_{2-y}^{\infty}{\rm e}^{-x} \,{\rm d} x \,{\rm d} y = ... = {1}/({8{\rm e}^2}) = I_3\hspace{0.05cm}.$$
Thus, the overall result is:
- $${\rm Pr} \left [ n_1 + n_2 > 2 \right ] = {\rm e}^{-2} \cdot ({1}/{4} +{1}/{2} +{1}/{8} +{1}/{8})= {\rm e}^{-2} \hspace{0.1cm}\hspace{0.15cm}\underline {\approx 13.5\%}\hspace{0.05cm}.$$