Difference between revisions of "Aufgaben:Exercise 4.11: Frequency Domain Consideration of the 4-QAM"
m (Text replacement - "Category:Aufgaben zu Modulationsverfahren" to "Category:Modulation Methods: Exercises") |
|||
| (11 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
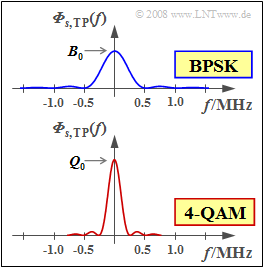
| − | [[File:Mod_A_4_10_vers2.png|right|frame| | + | [[File:Mod_A_4_10_vers2.png|right|frame|Power-spectral densities of <br>BPSK and 4-QAM]] |
| − | + | Taking as our starting point [[Modulation_Methods/Linear_Digital_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|$\rm BPSK$]] ("binary phase modulation") with a rectangular basic pulse $g_s(t)$ of width $T_{\rm B} = 1 \ \rm µ s$ and amplitude $s_0 = 2 \ \rm V$, this exercise aims to determine the power-spectral density $\rm (PSD)$ of the [[Modulation_Methods/Quadrature_Amplitude_Modulation#Signal_waveforms_for_4.E2.80.93QAM|4–QAM]] step by step. | |
| − | In | + | In [[Aufgaben:Exercise_4.7:_Spectra_of_ASK_and_BPSK|Exercise 4.7]], the power-spectral density ${\it Φ}_s(f)$ of the BPSK was determined for exactly these parameters. Using |
| − | :$$A = s_0^2 \cdot T_{\rm B} = 4 \cdot 10^{-6}\,{\rm V^2/Hz}$$ | + | :$$A = s_0^2 \cdot T_{\rm B} = 4 \cdot 10^{-6}\,{\rm V^2/Hz},$$ |
| − | + | one obtains the actual power-spectral density (in the bandpass range): | |
| − | :$${{\it \Phi}_s(f)} = {A}/{4} \cdot {\big [ {\rm | + | :$${{\it \Phi}_s(f)} = {A}/{4} \cdot {\big [ {\rm sinc}^2( T_{\rm B}\cdot (f - f_{\rm T})) + {\rm sinc}^2( T_{\rm B}\cdot (f + f_{\rm T}))\big ]}\hspace{0.05cm}.$$ |
| − | + | However, the top graph shows the power-spectral density ${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}$ of the equivalent low-pass signal German: "äquivalentes Tiefpass–Signal" ⇒ subscript: "TP). This is obtained from ${\it Φ}_s(f)$ by | |
| − | * | + | *truncating all components at negative frequencies, |
| − | * | + | *quadrupling the components at positive frequencies (note: a spectrum must be doubled, a PSD quadrupled), |
| − | + | *shifting by $f_{\rm T}$ to the left: | |
| − | * | + | :$${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)} = A \cdot {\rm sinc}^2(f \cdot T_{\rm B}). \hspace{0.2cm}$$ |
| − | :$${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)} = A \cdot {\rm | ||
| − | + | 4–QAM differs from the BPSK regarding the following details: | |
| − | * | + | * Splitting the binary source signal into two partial signals, each with half the bit rate, that is, with symbol duration $T = 2 · T_{\rm B}$. |
| − | * | + | * Multiplication of the partial signals with cosine and minus-sine, whose amplitudes $g_0$ are each smaller than $s_0$ by a factor of $\sqrt{2}$. |
| − | * Summation | + | * Summation of the two partial signals denoted by $s_{\cos}(t)$ nd $s_{–\sin}(t)$ : |
:$$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$ | :$$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$ | ||
| Line 27: | Line 26: | ||
| − | + | Hints: | |
| − | + | *This exercise belongs to the chapter [[Modulation_Methods/Quadrature_Amplitude_Modulation|"Quadrature Amplitude Modulation"]] $\rm (QAM)$. | |
| − | + | *Reference is also made to the page [[Modulation_Methods/Linear_Digital_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|"Binary Phase Shift Keying"]] $\rm (BPSK)$ in the previous chapter. | |
| − | + | * The power-spectral density $\rm (PSD)$ of a QAM component is identical to the comparable BPSK PSD: | |
| − | * | + | *Energies are to be specified in $\rm V^2s$; they thus refer to the reference resistance $R = 1 \ \rm \Omega$. |
| − | * | ||
| − | * | ||
| − | * | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the energy per bit ⇒ $E_{\rm B}$ for "binary phase shift keying" (BPSK)? |
|type="{}"} | |type="{}"} | ||
$E_{\rm B} \ = \ $ { 2 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | $E_{\rm B} \ = \ $ { 2 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | ||
| − | { | + | {What is the power-spectral density ${\it \Phi}_{s,\hspace{0.08cm} \cos, \hspace{0.08cm}{\rm TP}}(f )$ of the 4–QAM subsignal $s_{\cos}(t)$ in the equivalent low-pass representation? <br>What value $B_0 = {\it \Phi}_{s, \hspace{0.08cm}\cos, \hspace{0.08cm}{\rm TP}}(f = 0) $ is obtained at frquency $f = 0$? |
|type="{}"} | |type="{}"} | ||
$B_0 \ = \ $ { 4 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | $B_0 \ = \ $ { 4 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | ||
| − | { | + | {What is the power-spectral density ${\it \Phi}_{s,\hspace{0.08cm}{\rm TP}}(f )$ of the total 4–QAM signal $s(t)$? |
| − | <br> | + | <br>What value $Q_0 = {\it \Phi}_{s, \hspace{0.08cm}{\rm TP}}(f = 0) $ results here at frequency $f = 0$? |
|type="{}"} | |type="{}"} | ||
$Q_0 \ = \ $ { 8 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | $Q_0 \ = \ $ { 8 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | ||
| − | { | + | {What is the energy per bit ⇒ $E_{\rm B}$ for "quadrature amplitude modulation" (4-QAM)? |
|type="{}"} | |type="{}"} | ||
$E_{\rm B} \ = \ $ { 2 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | $E_{\rm B} \ = \ $ { 2 3% } $\ \cdot 10^{-6}\ \rm V^2/Hz$ | ||
| Line 62: | Line 58: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The power of the BPSK transmitted signal is equal to the intergral over the power-spectral density. |
| − | * | + | *If one integrates over the equivalent low-pass PSD, the factor $1/2$ must still be taken into account: |
| − | :$$P_{\rm BPSK} = \int_{ - \infty }^{+\infty} {{\it \Phi}_{s}(f)}\hspace{0.1cm} {\rm d}f = \frac{1}{2} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{A}{2} \cdot \int_{ - \infty }^{+\infty} {\rm | + | :$$P_{\rm BPSK} = \int_{ - \infty }^{+\infty} {{\it \Phi}_{s}(f)}\hspace{0.1cm} {\rm d}f = \frac{1}{2} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{A}{2} \cdot \int_{ - \infty }^{+\infty} {\rm sinc}^2(f T_{\rm B})\hspace{0.1cm} {\rm d}f = \frac{A}{2T_{\rm B}} \cdot \int_{ - \infty }^{+\infty} {\rm sinc}^2(x)\hspace{0.1cm} {\rm d}x =\frac{A}{2T_{\rm B}}$$ |
| − | :$$\text{ | + | :$$\text{With} \ \ A = 4 \cdot 10^{-6}\,{\rm V^2/Hz}\hspace{0.05cm}, \hspace{0.2cm} T_{\rm B}= 10^{-6}\,{\rm s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm BPSK} = 2\,{\rm V^2} ( = {s_0^2 }/{2})\hspace{0.05cm}.$$ |
| − | * | + | *Accordingly, the energy per bit is for BPSK: |
:$$E_{\rm B} = {P_{\rm BPSK} \cdot T_{\rm B}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | :$$E_{\rm B} = {P_{\rm BPSK} \cdot T_{\rm B}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | ||
| − | * | + | *Here again, the reference resistance is $1\ \rm Ω$. |
| − | '''(2)''' | + | '''(2)''' Due to the double symbol duration of 4-QAM $(T = 2 · T_{\rm B})$, the spectral function is only half as wide as compared to BPSK, but twice as high, and instead of $s_0$, the smaller value $g_0$ must now be considered. |
| − | * | + | *The PSD value at frequency $f = 0$ is thus: |
:$${\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) = \left ({s_0}/{\sqrt{2}} \right )^2 \cdot 2 \cdot T_{\rm B} ={s_0^2 \cdot T_{\rm B}} = B_0 \hspace{0.05cm}.$$ | :$${\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) = \left ({s_0}/{\sqrt{2}} \right )^2 \cdot 2 \cdot T_{\rm B} ={s_0^2 \cdot T_{\rm B}} = B_0 \hspace{0.05cm}.$$ | ||
| − | * | + | *Therefore, the result is exactly the same as for BPSK: |
:$$B_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) \hspace{0.15cm}\underline {= 4 \cdot 10^{-6}\,{\rm V^2/Hz}}$$ | :$$B_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) \hspace{0.15cm}\underline {= 4 \cdot 10^{-6}\,{\rm V^2/Hz}}$$ | ||
| − | '''(3)''' | + | '''(3)''' The second partial signal $s_{–\sin}(t)$ yields exactly the same contribution as the signal $s_{\cos}(t)$ just considered. |
| − | * | + | *Due to the orthogonality between the cosine and the minus-sine functions, the powers can be added and we get: |
:$$Q_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f = 0 ) = 2 \cdot B_0 \hspace{0.15cm}\underline {= 8 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | :$$Q_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f = 0 ) = 2 \cdot B_0 \hspace{0.15cm}\underline {= 8 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' Analogously to question '''(1)''', we get an energy per bit of: |
| − | :$$E_{\rm B} = \frac{1}{2} \cdot T_{\rm B} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{Q_0 \cdot T_{\rm B}}{2T} \cdot \int_{ - \infty }^{+\infty} {\rm | + | :$$E_{\rm B} = \frac{1}{2} \cdot T_{\rm B} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{Q_0 \cdot T_{\rm B}}{2T} \cdot \int_{ - \infty }^{+\infty} {\rm sinc}^2(f T_{\rm B})\hspace{0.1cm} {\rm d}f = |
\frac{Q_0 \cdot T_{\rm B}}{2T} = \frac{8 \cdot 10^{-6}\,{\rm V^2/Hz} \cdot 1\,{\rm \mu s}}{ 2 \cdot 2\,{\rm \mu s}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | \frac{Q_0 \cdot T_{\rm B}}{2T} = \frac{8 \cdot 10^{-6}\,{\rm V^2/Hz} \cdot 1\,{\rm \mu s}}{ 2 \cdot 2\,{\rm \mu s}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | ||
| − | * | + | *It can be seen that with the assumptions made here, the "energy per bit" of BPSK and 4-QAM coincide. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 98: | Line 94: | ||
| − | [[Category:Modulation Methods: Exercises|^4.3 | + | [[Category:Modulation Methods: Exercises|^4.3 Quadrature Amplitude Modulation^]] |
Latest revision as of 07:03, 18 April 2022
Taking as our starting point $\rm BPSK$ ("binary phase modulation") with a rectangular basic pulse $g_s(t)$ of width $T_{\rm B} = 1 \ \rm µ s$ and amplitude $s_0 = 2 \ \rm V$, this exercise aims to determine the power-spectral density $\rm (PSD)$ of the 4–QAM step by step.
In Exercise 4.7, the power-spectral density ${\it Φ}_s(f)$ of the BPSK was determined for exactly these parameters. Using
- $$A = s_0^2 \cdot T_{\rm B} = 4 \cdot 10^{-6}\,{\rm V^2/Hz},$$
one obtains the actual power-spectral density (in the bandpass range):
- $${{\it \Phi}_s(f)} = {A}/{4} \cdot {\big [ {\rm sinc}^2( T_{\rm B}\cdot (f - f_{\rm T})) + {\rm sinc}^2( T_{\rm B}\cdot (f + f_{\rm T}))\big ]}\hspace{0.05cm}.$$
However, the top graph shows the power-spectral density ${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}$ of the equivalent low-pass signal German: "äquivalentes Tiefpass–Signal" ⇒ subscript: "TP). This is obtained from ${\it Φ}_s(f)$ by
- truncating all components at negative frequencies,
- quadrupling the components at positive frequencies (note: a spectrum must be doubled, a PSD quadrupled),
- shifting by $f_{\rm T}$ to the left:
- $${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)} = A \cdot {\rm sinc}^2(f \cdot T_{\rm B}). \hspace{0.2cm}$$
4–QAM differs from the BPSK regarding the following details:
- Splitting the binary source signal into two partial signals, each with half the bit rate, that is, with symbol duration $T = 2 · T_{\rm B}$.
- Multiplication of the partial signals with cosine and minus-sine, whose amplitudes $g_0$ are each smaller than $s_0$ by a factor of $\sqrt{2}$.
- Summation of the two partial signals denoted by $s_{\cos}(t)$ nd $s_{–\sin}(t)$ :
- $$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Quadrature Amplitude Modulation" $\rm (QAM)$.
- Reference is also made to the page "Binary Phase Shift Keying" $\rm (BPSK)$ in the previous chapter.
- The power-spectral density $\rm (PSD)$ of a QAM component is identical to the comparable BPSK PSD:
- Energies are to be specified in $\rm V^2s$; they thus refer to the reference resistance $R = 1 \ \rm \Omega$.
Questions
Solution
- If one integrates over the equivalent low-pass PSD, the factor $1/2$ must still be taken into account:
- $$P_{\rm BPSK} = \int_{ - \infty }^{+\infty} {{\it \Phi}_{s}(f)}\hspace{0.1cm} {\rm d}f = \frac{1}{2} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{A}{2} \cdot \int_{ - \infty }^{+\infty} {\rm sinc}^2(f T_{\rm B})\hspace{0.1cm} {\rm d}f = \frac{A}{2T_{\rm B}} \cdot \int_{ - \infty }^{+\infty} {\rm sinc}^2(x)\hspace{0.1cm} {\rm d}x =\frac{A}{2T_{\rm B}}$$
- $$\text{With} \ \ A = 4 \cdot 10^{-6}\,{\rm V^2/Hz}\hspace{0.05cm}, \hspace{0.2cm} T_{\rm B}= 10^{-6}\,{\rm s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm BPSK} = 2\,{\rm V^2} ( = {s_0^2 }/{2})\hspace{0.05cm}.$$
- Accordingly, the energy per bit is for BPSK:
- $$E_{\rm B} = {P_{\rm BPSK} \cdot T_{\rm B}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$
- Here again, the reference resistance is $1\ \rm Ω$.
(2) Due to the double symbol duration of 4-QAM $(T = 2 · T_{\rm B})$, the spectral function is only half as wide as compared to BPSK, but twice as high, and instead of $s_0$, the smaller value $g_0$ must now be considered.
- The PSD value at frequency $f = 0$ is thus:
- $${\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) = \left ({s_0}/{\sqrt{2}} \right )^2 \cdot 2 \cdot T_{\rm B} ={s_0^2 \cdot T_{\rm B}} = B_0 \hspace{0.05cm}.$$
- Therefore, the result is exactly the same as for BPSK:
- $$B_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) \hspace{0.15cm}\underline {= 4 \cdot 10^{-6}\,{\rm V^2/Hz}}$$
(3) The second partial signal $s_{–\sin}(t)$ yields exactly the same contribution as the signal $s_{\cos}(t)$ just considered.
- Due to the orthogonality between the cosine and the minus-sine functions, the powers can be added and we get:
- $$Q_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f = 0 ) = 2 \cdot B_0 \hspace{0.15cm}\underline {= 8 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$
(4) Analogously to question (1), we get an energy per bit of:
- $$E_{\rm B} = \frac{1}{2} \cdot T_{\rm B} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{Q_0 \cdot T_{\rm B}}{2T} \cdot \int_{ - \infty }^{+\infty} {\rm sinc}^2(f T_{\rm B})\hspace{0.1cm} {\rm d}f = \frac{Q_0 \cdot T_{\rm B}}{2T} = \frac{8 \cdot 10^{-6}\,{\rm V^2/Hz} \cdot 1\,{\rm \mu s}}{ 2 \cdot 2\,{\rm \mu s}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$
- It can be seen that with the assumptions made here, the "energy per bit" of BPSK and 4-QAM coincide.