Exercise 4.11: On-Off Keying and Binary Phase Shift Keying
From LNTwww
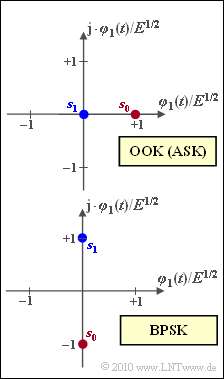
The graphic shows signal space constellations for carrier-modulated modulation methods:
- On–off keying (OOK), also known as Amplitude Shift Keying (ASK) in some books,
- Binary Phase Shift Keying (BPSK).
For the calculation of the error probability we start from the AWGN channel. In this case the error probability is (related to symbols or to bits alike):
- $$p_{\rm S} = p_{\rm B} = {\rm Q} \left ( \frac{ d/2}{ \sigma_n}\right ) \hspace{0.05cm}.$$
Here
- $d$ denotes the distance between the signal space points, and
- $\sigma_n^2 = N_0/2$ the variance of the AWGN noise.
In the questions from (3) onwards, reference is also made to the mean symbol energy $E_{\rm S}$.
Notes:
- The exercise belongs to the chapter "Carrier Frequency Systems with Coherent Demodulation".
- Reference is also made to the chapter "Linear Digital Modulation – Coherent Demodulation" and the chapter "Linear Digital Modulation" in the book "Modulation Methods".
- For the complementary Gaussian error function, use the following approximation:
- $${\rm Q}(x) \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$
Questions
Solution
(1) Both On–Off Keying (OOK) and Binary Phase Shift Keying (BPSK) are binary modulation methods:
- $$\underline{b = 1 }\hspace{0.05cm},\hspace{0.5cm} \underline{M = 2} \hspace{0.05cm}.$$
(2) Solution 2 is correct, recognizable by the imaginary basis function $\varphi_2(t) = {\rm j} \cdot \varphi_1(t)$.
- If described in the band-pass range, the basis functions would be cosine and (minus)sine real.
(3) The given equation is for On–Off Keying (OOK) with
- $d = \sqrt {E}$,
- $E_{\rm S} = E/2$ (assuming equally probable symbols $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$) and
- $\sigma_n^2 = N_0/2$:
- $$p_{\rm S} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm Q} \left ( \frac{ d/2}{ \sigma_n}\right )= {\rm Q} \left ( \frac{ \sqrt{E}/2}{ \sqrt{N_0/2}}\right ) = {\rm Q} \left ( \sqrt{ \frac{ E/2}{ N_0} }\right ) = {\rm Q} \left ( \sqrt{ { E_{\rm S}}/{ N_0} }\right ) \hspace{0.05cm}.$$
- For $E_{\rm S}/N_0 = 9 = 3^2$ this results in:
- $$p_{\rm S} = {\rm Q} (3) \approx \frac{1}{\sqrt{2\pi} \cdot 3} \cdot {\rm e}^{-9/2} = \underline{14.8 \cdot 10^{-4}} \hspace{0.05cm}.$$
- Accordingly, for $10 \cdot {\rm lg} \, (E_{\rm S}/N_0) = 12 \ \rm dB$ ⇒ $E_{\rm S}/N_0 = 15.85$:
- $$p_{\rm S} = {\rm Q} (\sqrt{15.85}) \approx \frac{1}{\sqrt{2\pi\cdot 15.85} } \cdot {\rm e}^{-15.85/2} = \underline{0.362 \cdot 10^{-4}} \hspace{0.05cm}.$$
(4) In contrast to subtask (3), Binary Phase Shift Keying (BPSK) applies
- $d = 2 \cdot \sqrt {E}$,
- $E_{\rm S} = E$,
both even independent of the occurrence probabilities for $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$.
- It follows:
- $$p_{\rm S} = {\rm Q} \left ( \frac{ \sqrt{E_{\rm S}}}{ \sqrt{N_0/2}}\right ) = {\rm Q} \left ( \sqrt{ { 2E_{\rm S}}/{ N_0} }\right ) \hspace{0.05cm}.$$
- With $E_{\rm S}/N_0 = 9$, this results in the numerical value:
- $$p_{\rm S} = {\rm Q} (\sqrt{18}) \approx \frac{1}{\sqrt{2\pi\cdot 18} } \cdot {\rm e}^{-18/2} = \underline{117 \cdot 10^{-8}} \hspace{0.05cm}.$$
- And with $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 12 \ \rm dB$ ⇒ $2E_{\rm S}/N_0 = 31.7$:
- $$p_{\rm S} = {\rm Q} (\sqrt{31.7}) \approx \frac{1}{\sqrt{2\pi\cdot 31.7} } \cdot {\rm e}^{-31.7/2} = \underline{0.926 \cdot 10^{-8}}\hspace{0.05cm}.$$