Difference between revisions of "Aufgaben:Exercise 4.11Z: Error Probability with QAM"
From LNTwww
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| (15 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1721__Mod_Z_4_10.png|right|frame| | + | [[File:P_ID1721__Mod_Z_4_10.png|right|frame|Table with two different "Gaussian error functions"]] |
| − | + | We now make the following assumptions: | |
| − | * | + | * binary bipolar amplitude coefficients $a_ν ∈ \{±1\}$, |
| − | * | + | * rectangular basic transmission pulse with amplitude $s_0$ and bit duration $T_{\rm B}$, |
| − | * | + | * AWGN noise with noise power density $N_0$, |
| − | * | + | * a receiver according to the matched-filter principle, |
| − | * | + | * the best possible demodulation and detection. |
| − | + | The bit error probability of binary phase modulation $\rm (BPSK)$ under these conditions can be calculated using the following equations: | |
:$$ p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ({s_0}/{\sigma_d } \right ), \hspace{0.2cm} E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/{T_{\rm B} }$$ | :$$ p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ({s_0}/{\sigma_d } \right ), \hspace{0.2cm} E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/{T_{\rm B} }$$ | ||
:$$\Rightarrow \hspace{0.3cm} p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$ | :$$\Rightarrow \hspace{0.3cm} p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$ | ||
| − | + | *The corresponding equations of $\rm 4–QAM$ are: | |
:$$ p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( {g_0}/{\sigma_d } \right ), \hspace{0.2cm}g_{0} = {s_0}/{\sqrt{2}}, \hspace{0.2cm}E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/({2 \cdot T_{\rm B} }).$$ | :$$ p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( {g_0}/{\sigma_d } \right ), \hspace{0.2cm}g_{0} = {s_0}/{\sqrt{2}}, \hspace{0.2cm}E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/({2 \cdot T_{\rm B} }).$$ | ||
| − | + | *Here it is taken into account that – in order to achieve the same transmission energy per bit as with BPSK – one must reduce the amplitude $g_0$ of the rectangular pulses in the two sub-branches of 4-QAM by a factor of $\sqrt{2}$ . | |
| + | *The envelope is then equal to $s_0$ for both systems. | ||
| − | + | ||
| − | * | + | |
| − | * | + | Hints: |
| − | * | + | *This exercise belongs to the chapter [[Modulation_Methods/Quadrature_Amplitude_Modulation|"Quadrature Amplitude Modulation"]]. |
| − | * | + | *Reference is also made to the page [[Modulation_Methods/Linear_Digital_Modulation#Error_probabilities_-_a_brief_overview|"Error probabilities – a brief overview"]] in the previous chapter. |
| − | *In | + | * Always assume the following numerical values: $s_0 = 2\,{\rm V}, \hspace{0.05cm} N_0 = 0.25 \cdot 10^{-6}\,{\rm V^2/Hz}\hspace{0.05cm}.$ |
| − | * | + | *The bit duration is $T_{\rm B} = 1 \ \rm µ s$ (question 1) and $T_{\rm B} = 2 \ \rm µ s$ (from question 2 onwards). |
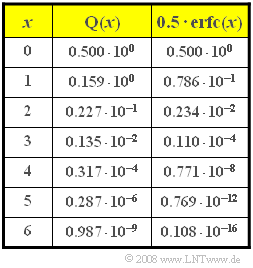
| + | *In the table, the two common Gaussian error functions ${\rm Q}(x)$ and $1/2 \cdot {\rm erfc}(x)$ are given. | ||
| + | *Energies are to be given in $\rm V^2s$; thus, they refer to the reference resistance $R = 1 \ \rm \Omega$. | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What error probability $p_\text{B, BPSK}$ results for '''BPSK''' when $T_{\rm B} = 1 \ \rm µ s$? |
|type="{}"} | |type="{}"} | ||
$p_\text{B, BPSK} \ = \ $ { 0.317 3% } $\ \rm 10^{-4}$ | $p_\text{B, BPSK} \ = \ $ { 0.317 3% } $\ \rm 10^{-4}$ | ||
| − | { | + | {What error probability $p_\text{B, BPSK}$ results for '''BPSK''' when $T_{\rm B} = 2 \ \rm µ s$? |
|type="{}"} | |type="{}"} | ||
$p_\text{B, BPSK} \ = \ $ { 0.771 3% } $\ \rm 10^{-8}$ | $p_\text{B, BPSK} \ = \ $ { 0.771 3% } $\ \rm 10^{-8}$ | ||
| − | { | + | {What error probability $p_\text{B, 4-QAM}$ is obtained for '''4-QAM''' when $E_{\rm B} = 4 · 10^{–6} \ \rm V^2s$? |
|type="{}"} | |type="{}"} | ||
$p_\text{B, 4-QAM} \ = \ $ { 0.771 3% } $\ \rm 10^{-8}$ | $p_\text{B, 4-QAM} \ = \ $ { 0.771 3% } $\ \rm 10^{-8}$ | ||
| − | { | + | {Which statements apply if we consider only one branch $\rm (I$ or $\rm Q)$ of the 4–QAM? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The same result is obtained as for the entire 4-QAM. |
| − | - | + | - The distance of the noisless samples from the threshold $E=0$ is the same $(s_0)$ as in BPSK. |
| − | - | + | - The same result is obtained for the noise power as in BPSK. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' With the values given, for "Binary Phase Shift Keying" (BPSK), one gets: |
| − | :$$E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} = \frac{1}{2}\cdot (2\,{\rm V})^2 \cdot 1\,{\rm | + | :$$E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} = \frac{1}{2}\cdot (2\,{\rm V})^2 \cdot 1\,{\rm µ s} = 2 \cdot 10^{-6}\,{\rm V^2s} |
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {E_{\rm B}}/{N_0} = \frac {2 \cdot 10^{-6}\,{\rm V^2s}}{0.25 \cdot 10^{-6}\,{\rm V^2/Hz}} = 8$$ | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {E_{\rm B}}/{N_0} = \frac {2 \cdot 10^{-6}\,{\rm V^2s}}{0.25 \cdot 10^{-6}\,{\rm V^2/Hz}} = 8$$ | ||
:$$ \Rightarrow \hspace{0.3cm} p_\text{B, BPSK} = {\rm Q}\left ( \sqrt{16} \right ) = {\rm Q}\left ( 4 \right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{8}\right )\hspace{0.05cm}.$$ | :$$ \Rightarrow \hspace{0.3cm} p_\text{B, BPSK} = {\rm Q}\left ( \sqrt{16} \right ) = {\rm Q}\left ( 4 \right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{8}\right )\hspace{0.05cm}.$$ | ||
| − | + | *Based on the given $x$–values in the table, it is convenient to use the first equation in this subtask: | |
:$$p_\text{B, BPSK} = {\rm Q}\left ( 4 \right ) \hspace{0.15cm}\underline {= 0.317 \cdot 10^{-4} }\hspace{0.05cm}.$$ | :$$p_\text{B, BPSK} = {\rm Q}\left ( 4 \right ) \hspace{0.15cm}\underline {= 0.317 \cdot 10^{-4} }\hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | |
| + | '''(2)''' With twice the bit duration, the energy is also twice as large: $E_{\rm B} = 4 · 10^{–6} \ \rm V^2s$ ⇒ $E_{\rm B}/N_0 = 16$. | ||
| + | *It follows that: | ||
:$$p_\text{B, BPSK} = {\rm Q}\left ( \sqrt{32} \right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{16}\right ) ={1}/{2}\cdot {\rm erfc}\left ( 4\right ) \hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}}\hspace{0.05cm}.$$ | :$$p_\text{B, BPSK} = {\rm Q}\left ( \sqrt{32} \right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{16}\right ) ={1}/{2}\cdot {\rm erfc}\left ( 4\right ) \hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}}\hspace{0.05cm}.$$ | ||
| − | + | *For pragmatic reasons, the last column of the table was used here. | |
| + | |||
| − | '''(3)''' | + | |
| + | '''(3)''' Substituting the equations given for the 4-QAM into each other, we get the same result as for the BPSK: | ||
:$$p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \equiv p_\text{B, BPSK}.$$ | :$$p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \equiv p_\text{B, BPSK}.$$ | ||
| − | + | *Also, since the energy per bit has not changed from subtask '''(2)''', the same error probability will arise: | |
:$$p_{\rm B, \hspace{0.05cm}4-QAM}= {\rm Q}\left ( \sqrt{32} \right ) = {1}/{2}\cdot {\rm erfc}\left ( 4\right ) \hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}}\hspace{0.05cm}.$$ | :$$p_{\rm B, \hspace{0.05cm}4-QAM}= {\rm Q}\left ( \sqrt{32} \right ) = {1}/{2}\cdot {\rm erfc}\left ( 4\right ) \hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}}\hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | |
| − | * | + | '''(4)''' Only <u>Answer 1</u> is correct: |
| − | * | + | *Of course the error probability is the same in the two branches. Why would it not be? |
| − | * | + | *This would no longer be true with a phase offset between the transmitter and receiver though. |
| + | *However, the distance of the useful samples from the threshold is $g_0$ here and thus smaller than the envelope $s_0$ of the entire 4-QAM by a factor of $\sqrt{2}$ . | ||
| + | *However, if the inphase branch (or the quadrature branch) is considered as a stand-alone BPSK, the noise power is also half that of BPSK because of the lower symbol rate. Therefore, the error probability remains the same. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 84: | Line 93: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^4.3 Quadrature Amplitude Modulation^]] |
Latest revision as of 08:43, 18 April 2022
We now make the following assumptions:
- binary bipolar amplitude coefficients $a_ν ∈ \{±1\}$,
- rectangular basic transmission pulse with amplitude $s_0$ and bit duration $T_{\rm B}$,
- AWGN noise with noise power density $N_0$,
- a receiver according to the matched-filter principle,
- the best possible demodulation and detection.
The bit error probability of binary phase modulation $\rm (BPSK)$ under these conditions can be calculated using the following equations:
- $$ p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ({s_0}/{\sigma_d } \right ), \hspace{0.2cm} E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/{T_{\rm B} }$$
- $$\Rightarrow \hspace{0.3cm} p_{\rm B, \hspace{0.05cm}BPSK} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$
- The corresponding equations of $\rm 4–QAM$ are:
- $$ p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( {g_0}/{\sigma_d } \right ), \hspace{0.2cm}g_{0} = {s_0}/{\sqrt{2}}, \hspace{0.2cm}E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/({2 \cdot T_{\rm B} }).$$
- Here it is taken into account that – in order to achieve the same transmission energy per bit as with BPSK – one must reduce the amplitude $g_0$ of the rectangular pulses in the two sub-branches of 4-QAM by a factor of $\sqrt{2}$ .
- The envelope is then equal to $s_0$ for both systems.
Hints:
- This exercise belongs to the chapter "Quadrature Amplitude Modulation".
- Reference is also made to the page "Error probabilities – a brief overview" in the previous chapter.
- Always assume the following numerical values: $s_0 = 2\,{\rm V}, \hspace{0.05cm} N_0 = 0.25 \cdot 10^{-6}\,{\rm V^2/Hz}\hspace{0.05cm}.$
- The bit duration is $T_{\rm B} = 1 \ \rm µ s$ (question 1) and $T_{\rm B} = 2 \ \rm µ s$ (from question 2 onwards).
- In the table, the two common Gaussian error functions ${\rm Q}(x)$ and $1/2 \cdot {\rm erfc}(x)$ are given.
- Energies are to be given in $\rm V^2s$; thus, they refer to the reference resistance $R = 1 \ \rm \Omega$.
Questions
Solution
(1) With the values given, for "Binary Phase Shift Keying" (BPSK), one gets:
- $$E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} = \frac{1}{2}\cdot (2\,{\rm V})^2 \cdot 1\,{\rm µ s} = 2 \cdot 10^{-6}\,{\rm V^2s} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {E_{\rm B}}/{N_0} = \frac {2 \cdot 10^{-6}\,{\rm V^2s}}{0.25 \cdot 10^{-6}\,{\rm V^2/Hz}} = 8$$
- $$ \Rightarrow \hspace{0.3cm} p_\text{B, BPSK} = {\rm Q}\left ( \sqrt{16} \right ) = {\rm Q}\left ( 4 \right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{8}\right )\hspace{0.05cm}.$$
- Based on the given $x$–values in the table, it is convenient to use the first equation in this subtask:
- $$p_\text{B, BPSK} = {\rm Q}\left ( 4 \right ) \hspace{0.15cm}\underline {= 0.317 \cdot 10^{-4} }\hspace{0.05cm}.$$
(2) With twice the bit duration, the energy is also twice as large: $E_{\rm B} = 4 · 10^{–6} \ \rm V^2s$ ⇒ $E_{\rm B}/N_0 = 16$.
- It follows that:
- $$p_\text{B, BPSK} = {\rm Q}\left ( \sqrt{32} \right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{16}\right ) ={1}/{2}\cdot {\rm erfc}\left ( 4\right ) \hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}}\hspace{0.05cm}.$$
- For pragmatic reasons, the last column of the table was used here.
(3) Substituting the equations given for the 4-QAM into each other, we get the same result as for the BPSK:
- $$p_{\rm B, \hspace{0.05cm}4-QAM} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \equiv p_\text{B, BPSK}.$$
- Also, since the energy per bit has not changed from subtask (2), the same error probability will arise:
- $$p_{\rm B, \hspace{0.05cm}4-QAM}= {\rm Q}\left ( \sqrt{32} \right ) = {1}/{2}\cdot {\rm erfc}\left ( 4\right ) \hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}}\hspace{0.05cm}.$$
(4) Only Answer 1 is correct:
- Of course the error probability is the same in the two branches. Why would it not be?
- This would no longer be true with a phase offset between the transmitter and receiver though.
- However, the distance of the useful samples from the threshold is $g_0$ here and thus smaller than the envelope $s_0$ of the entire 4-QAM by a factor of $\sqrt{2}$ .
- However, if the inphase branch (or the quadrature branch) is considered as a stand-alone BPSK, the noise power is also half that of BPSK because of the lower symbol rate. Therefore, the error probability remains the same.