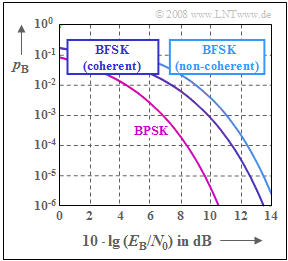
Exercise 4.16: Comparison between Binary PSK and Binary FSK
The graph shows the bit error probability for binary FSK modulation $\rm (BFSK)$ in
- coherent demodulation , as well as in
- non-coherent demodulation
in comparison with binary phase modulation $\rm (BPSK)$.
Orthogonality is always assumed. For coherent demodulation, the modulation index can be a multiple of $h = 0.5$ , so that the middle plot can also apply to Minimum Shift Keying $\rm (MSK)$ . In contrast, for non-coherent demodulation of BFSK, the modulation index must be a multiple of $h = 1$ .
This system comparison is once again based on the AWGN channel , characterized by the relationship $E_{\rm B}/N_0$. The equations for the bit error probabilities are as follows
- for Binary Phase Shift Keying $\rm (BPSK)$:
- $$p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ),$$
- for Binary Frequency Shift Keying $\rm (BFSK)$ with coherent demodulation:
- $$p_{\rm B} = {\rm Q}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/(2 N_0 )} \hspace{0.1cm}\right ),$$
- for Binary Frequency Shift Keying $\rm (BFSK)$ with incoherent demodulation:
- $$p_{\rm B} = {1}/{2} \cdot {\rm e}^{- E_{\rm B}/{(2N_0) }}\hspace{0.05cm}.$$
It was shown in Exercise 4.8 , that for BPSK, the log ratio $10 · \lg \ E_{\rm B}/N_0$ must be at least $9.6 \ \rm dB$ so that the bit error probability does not exceed $p_{\rm B} = 10^{–5}$ .
Hints:
- This exercise belongs to the chapter Nonlinear_Digital_Modulation.
- However, reference is also made to the page Linear Digital Modulation.
- Use the approximation $\lg(2) ≈ 0.3$.
Questions
Solution
- In other words: the coherent BFSK curve is $10 · \lg (2) ≈ 3 \ \rm dB$ to the right of the the BPSK curve.
- Thus, to guarantee $p_{\rm B} \le 10^{–5}$ it must hold that:
- $$10 \cdot {\rm lg}\hspace{0.05cm}{E_{\rm B}} /{N_{\rm 0}}= 9.6\,\,{\rm dB} + 3\,\,{\rm dB} = \underline{12.6\,\,{\rm dB}}\hspace{0.05cm}.$$
(2) Answer 2 is correct:
- The equation given does not just hold for MSK $($this is a FSK with $h = 0.5)$, but also for every form of orthogonal FSK.
- This is the case whenever the modulation index $h$ is an integer multiple of $0.5$ , such as when $h = 1$.
- When $h = 0.7$ , there is no orthogonal FSK.
(3) From the inverse function of the equation given we get:
- $$\frac{E_{\rm B}} {2 \cdot N_{\rm 0}}= {\rm ln}\hspace{0.05cm}\frac{1}{2 p_{\rm B}}= {\rm ln}(50000)\approx 10.82 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{E_{\rm B}} /{N_{\rm 0}}= 21.64 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.05cm}{E_{\rm B}}/ {N_{\rm 0}}\approx \underline{13.4\,\,{\rm dB}}\hspace{0.05cm}.$$
(4) From $10 · \lg \ E_{\rm B}/N_0 = 12.6 \ \rm dB$ it follows that:
- $${E_{\rm B}} /{N_{\rm 0}}= 10^{1.26} \approx 16.8 \hspace{0.25cm}\Rightarrow \hspace{0.25cm} ({E_{\rm B}} /{N_{\rm 0}})/2 \approx 8.4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} p_{\rm B} = {1}/{2} \cdot {\rm e}^{- 8.4} \approx \underline{1.12 \cdot 10^{-4}}\hspace{0.05cm}.$$
This means that for the same $E_{\rm B}/N_0$, the error probability of incoherent demodulation is increased by a factor of $11$ compared to that of coherent demodulation (see answer to question 1) .