Aufgaben:Exercise 4.18Z: BER of Coherent and Non-Coherent FSK

• Return to book

Bit error probabilities of
BPSK and BFSK

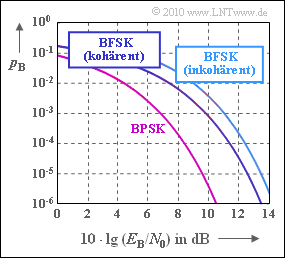
The diagram shows the bit error probability for a binary  "FSK modulation"  (BFSK) with

• coherent demodulation or
• incoherent demodulation

in comparison with binary phase modulation (BPSK). Orthogonality is always assumed. For coherent demodulation, the modulation index  $h$  can be a multiple of  $0.5$,  so that the average curve is also valid for Minimum Shift Keying  (MSK). On the other hand, for non-coherent demodulation of an FSK, the modulation index  $h$  must be a multiple of  $1$. 

This system comparison is based on the AWGN channel, characterized by the ratio  $E_{\rm B}/N_0$. The equations for the bit error probabilities are as follows for

• Binary Frequency Shift Keying  (BFSK) with coherent demodulation:

$$p_{\rm B} = {\rm Q } \left ( \sqrt {{E_{\rm B}}/{N_0} }\right ) \hspace{0.05cm}.$$

• Binary Frequency Shift Keying  (BFSK) with incoherent demodulation:

$$p_{\rm B} = {1}/{2} \cdot {\rm e}^{- E_{\rm B}/{(2N_0) }}\hspace{0.05cm}.$$

• Binary Phase Shift Keying  (BPSK), only coherent demodulation possible:

$$p_{\rm B} = {\rm Q } \left ( \sqrt {{2 \cdot E_{\rm B}}/{N_0} }\right ) \hspace{0.05cm}.$$

For BPSK, the log ratio  $10 \cdot {\rm lg} \, (E_{\rm B}/N_0)$  must be at least  $9.6 \, \rm dB$  so that the bit error probability does not exceed the value  $p_{\rm B} = 10^{\rm -5}$. 

For binary modulation methods,  $p_{\rm B}$  can also be replaced by  $p_{\rm S}$  and  $E_{\rm B}$  by  $E_{\rm S}$.  Then we speak of the symbol error probability  $p_{\rm S}$  and the symbol energy  $E_{\rm S}$.

Notes:

• The exercise belongs to the chapter  "Carrier Frequency Systems with Non-Coherent Demodulation".
• However, reference is also made to the chapter  "Carrier Frequency Systems with Coherent Demodulation".
• Further information can be found in the book "Modulation Methods".
• Use the approximation  ${\rm lg}(2) \approx 0.3$.

Questions

1

For FSK and  coherent demodulation,  which  $E_{\rm B}/N_0$  is required to satisfy the requirement  $p_{\rm B} ≤ 10^{\rm -5}$?

$10 \cdot {\rm lg} \, E_{\rm B}/N_0 \ = \ $ $\ \rm dB$

2

Are the following statements correct:   The same result as in (1) is obtained for

	the coherent FSK with modulation index  $\eta = 0.7$,
	the coherent FSK with modulation index  $\eta = 1$.

3

For FSK with modulation index  $h = 1$  and non-coherent demodulation,  which  $E_{\rm B}/N_0$  is required for  $p_{\rm B} ≤ 10^{\rm -5}$  to be satisfied?

$10 \cdot {\rm lg} \, E_{\rm B}/N_0 \ = \ $ $\ \rm dB$

4

What is the error probability with  $10 \cdot {\rm lg} \, E_{\rm B}/N_0 = 12.6 \ \rm dB$  for FSK and non-coherent demodulation?

$p_{\rm B} \ = \ $ $\ \%$

Solution

Solution

(1)  A comparison of the equations in the information section makes it clear that for binary FSK with coherent demodulation, the AWGN ratio $E_{\rm B}/N_0$ must be doubled to achieve the same error probability as for BPSK.

• In other words:   The coherent BFSK curve is $10 \cdot {\rm lg} \, (2) \approx 3 \ \rm dB$ to the right of the BPSK curve. To guarantee $p_{\rm B} ≤ 10^{\rm –5}$, it must hold:

$$10 \cdot {\rm lg}\hspace{0.05cm} {E_{\rm B}}/ {N_{\rm 0}}\approx 9.6\,\,{\rm dB} + 3\,\,{\rm dB}\hspace{0.15cm} \underline{=12.6\,\,{\rm dB}}\hspace{0.05cm}.$$

(2)  Solution 2 is correct:

• The given equation is valid not only for the MSK (this is an FSK with $h = 0.5$), but for any form of orthogonal FSK.
• Such a FSK exists if the modulation index $h$ is an integer multiple of $0.5$, for example for $h = 1$.
• With $h = 0.7$ there is no orthogonal FSK.
• It can be shown that for $h = 0.7$ there is even a smaller error probability than with orthogonal FSK.
• With $10 \cdot {\rm lg} \, E_{\rm B}/N_0 = 12.6 \ \rm dB$ one even achieves $p_{\rm B} \approx 10^{\rm –6}$, here, i.e. an improvement by one power of ten.

(3)  From the inverse function of the given equation one obtains:

$$\frac{E_{\rm B}} {2 \cdot N_{\rm 0}}= {\rm ln}\hspace{0.05cm}\frac{1}{2 p_{\rm B}}= {\rm ln}(50000)\approx 10.82\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {E_{\rm B}}/ {N_{\rm 0}}= 21.64 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.09cm} {E_{\rm B}}/ {N_{\rm 0}}\hspace{0.15cm} \underline{\approx 13.4\,\,{\rm dB}}\hspace{0.05cm}.$$

(4)  From $10 \cdot {\rm lg} \, E_{\rm B}/N_0 = 12.6 \ \rm dB$ follows:

$${E_{\rm B}} /{N_{\rm 0}}= 10^{1.26} \approx 16.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{E_{\rm B}} {2 \cdot N_{\rm 0}}\approx 8.4 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B} = {1}/{2} \cdot {\rm e}^{- 8.4}\hspace{0.15cm} \underline{ \approx 0.012 \%}\hspace{0.05cm}.$$

This means:   For the same $E_{\rm B}/N_0$, the error probability for non-coherent demodulation is increased by a factor of about 11 compared to coherent demodulation according to subtask (1).