Difference between revisions of "Aufgaben:Exercise 4.5: On the Extrinsic L-values again"
| (2 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
[[File:P_ID3026__KC_A_4_5_v2.png|right|frame|Table for first $L_{\rm E}(i)$ approach]] | [[File:P_ID3026__KC_A_4_5_v2.png|right|frame|Table for first $L_{\rm E}(i)$ approach]] | ||
| − | We assume as in the [[Channel_Coding/Soft-in_Soft-Out_Decoder# | + | We assume as in the [[Channel_Coding/Soft-in_Soft-Out_Decoder#Calculation_of_extrinsic_log_likelihood_ratios|"theory section"]] the "single parity–check code" $\rm SPC \, (3, \, 2, \, 2)$. |
The possible code words are $\underline{x} \hspace{-0.01cm}\in \hspace{-0.01cm} | The possible code words are $\underline{x} \hspace{-0.01cm}\in \hspace{-0.01cm} | ||
| Line 25: | Line 25: | ||
#However, the code is well suited for demonstration purposes because of the manageable effort involved. | #However, the code is well suited for demonstration purposes because of the manageable effort involved. | ||
#With "iterative symbol-wise decoding" one can also correct one error. | #With "iterative symbol-wise decoding" one can also correct one error. | ||
| − | #In the present code, the extrinsic L–values $\underline{L}_{\rm E} = \big (L_{\rm E}(1), \ L_{\rm E}(2), \ L_{\rm E}(3)\big )$ must be calculated according to the following equation: | + | #In the present code, the extrinsic $L$–values $\underline{L}_{\rm E} = \big (L_{\rm E}(1), \ L_{\rm E}(2), \ L_{\rm E}(3)\big )$ must be calculated according to the following equation: |
:$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} \right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} \hspace{0.05cm}\right ]}.$$ | :$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} \right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} \hspace{0.05cm}\right ]}.$$ | ||
| Line 36: | Line 36: | ||
:$$L_{\rm E}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \right ] \hspace{0.05cm}.$$ | :$$L_{\rm E}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \right ] \hspace{0.05cm}.$$ | ||
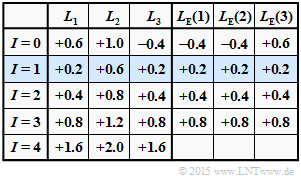
| − | '''(1)''' This $L_{\rm E}(i)$ approach underlies the results table above $($red entries$)$, assuming the following a-posteriori L–values: | + | '''(1)''' This $L_{\rm E}(i)$ approach underlies the results table above $($red entries$)$, assuming the following a-posteriori $L$–values: |
:$$\underline {L}_{\rm APP} = (+1.0\hspace{0.05cm},\hspace{0.05cm}+0.4\hspace{0.05cm},\hspace{0.05cm}-1.0) \hspace{0.5cm}\Rightarrow \hspace{0.5cm} | :$$\underline {L}_{\rm APP} = (+1.0\hspace{0.05cm},\hspace{0.05cm}+0.4\hspace{0.05cm},\hspace{0.05cm}-1.0) \hspace{0.5cm}\Rightarrow \hspace{0.5cm} | ||
L_1 = +1.0\hspace{0.05cm},\hspace{0.15cm} | L_1 = +1.0\hspace{0.05cm},\hspace{0.15cm} | ||
| Line 42: | Line 42: | ||
L_3 = -1.0\hspace{0.05cm}.$$ | L_3 = -1.0\hspace{0.05cm}.$$ | ||
| − | '''(2)''' The extrinsic $L$–values for the zeroth iteration result in (derivation in [[Aufgaben:Exercise_4.5Z:_Tangent_Hyperbolic_and_Inverse| | + | '''(2)''' The extrinsic $L$–values for the zeroth iteration result in $($derivation in [[Aufgaben:Exercise_4.5Z:_Tangent_Hyperbolic_and_Inverse|$\text{Exercise 4.5Z})$]]: |
:$$L_{\rm E}(1) = -0.1829, \ L_{\rm E}(2) = -0.4337, \ L_{\rm E}(3) = +0.1829.$$ | :$$L_{\rm E}(1) = -0.1829, \ L_{\rm E}(2) = -0.4337, \ L_{\rm E}(3) = +0.1829.$$ | ||
| − | '''(3)''' The a posteriori values at the beginning of the first iteration are thus | + | '''(3)''' The a-posteriori $L$–values at the beginning of the first iteration are thus |
| − | :$$\underline{ | + | :$$\underline{L_{\rm APP} }^{(I=1)} = \underline{L_{\rm APP} }^{(I=0)} + \underline{L}_{\hspace{0.02cm}\rm E}^{(I=0)} = |
(+0.8171\hspace{0.05cm},\hspace{0.05cm}-0.0337\hspace{0.05cm},\hspace{0.05cm}-0.8171) | (+0.8171\hspace{0.05cm},\hspace{0.05cm}-0.0337\hspace{0.05cm},\hspace{0.05cm}-0.8171) | ||
\hspace{0.05cm} . $$ | \hspace{0.05cm} . $$ | ||
| − | '''(4)''' From this, the new extrinsic values for the iteration loop $I = 1$ are as follows: | + | '''(4)''' From this, the new extrinsic $L$–values for the iteration loop $I = 1$ are as follows: |
:$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(-0.0337/2) \cdot {\rm tanh}(-0.8171/2) \big ] = 0.0130 = -L_{\rm E}(3)\hspace{0.05cm},$$ | :$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(-0.0337/2) \cdot {\rm tanh}(-0.8171/2) \big ] = 0.0130 = -L_{\rm E}(3)\hspace{0.05cm},$$ | ||
:$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(+0.8171/2) \cdot {\rm tanh}(-0.8171/2) \big ] = - 0.3023\hspace{0.05cm}.$$ | :$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(+0.8171/2) \cdot {\rm tanh}(-0.8171/2) \big ] = - 0.3023\hspace{0.05cm}.$$ | ||
| − | Further, one can see from the above table: | + | Further, one can see from the above table: |
| − | * A hard decision according to the signs before the first iteration $(I = 0)$ fails, since $(+1, +1, -1)$ is not a valid $\rm SPC \, (3, \, 2, \, 2)$& | + | * A hard decision according to the signs before the first iteration $(I = 0)$ fails, since $(+1, +1, -1)$ is not a valid $\rm SPC \, (3, \, 2, \, 2)$ code word. |
| − | * But already after $I = 1$ iterations, a hard decision yields a valid code word, namely $\underline{x}_2 = (+1, -1, -1)$. Also in later graphs, the rows with correct | + | |
| + | * But already after $I = 1$ iterations, a hard decision yields a valid code word, namely $\underline{x}_2 = (+1, -1, -1)$. | ||
| + | |||
| + | *Also in later graphs, the rows with correct hard decisions for the first time are highlighted in blue. | ||
| + | |||
* Hard decisions after further iterations $(I ≥ 2)$ each lead to the same code word $\underline{x}_2$. This statement is not only valid for this example, but in general. | * Hard decisions after further iterations $(I ≥ 2)$ each lead to the same code word $\underline{x}_2$. This statement is not only valid for this example, but in general. | ||
| − | Besides, in this exercise we consider a '''second $L_{\rm E}(i)$ approach''', which is given here for the example of the first symbol $(i = 1)$: | + | Besides, in this exercise we consider a »'''second $L_{\rm E}(i)$ approach'''«, which is given here for the example of the first symbol $(i = 1)$: |
| − | :$${\rm sign} \big[L_{\rm E}(1)\big] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} \big[L_{\rm E}(2)\big] \cdot {\rm sign} \big[L_{\rm E}(3)\big]\hspace{0.05cm}, | + | :$${\rm sign} \big[L_{\rm E}(1)\big] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} \big[L_{\rm E}(2)\big] \cdot {\rm sign} \big[L_{\rm E}(3)\big]\hspace{0.05cm},$$ |
| − | |L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) \hspace{0.05cm}.$$ | + | :$$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) \hspace{0.05cm}.$$ |
| + | |||
| + | This second approach is based on the assumption that the reliability of $L_{\rm E}(i)$ is essentially determined by the most unreliable neighbor symbol. The better $($larger$)$ the input log likelihood ratio is completely disregarded. | ||
| − | + | Let us consider two examples for this: | |
| − | '''(1)''' For $L_2 = 1.0$ and $L_3 = 5.0$ we get | + | '''(1)''' For $L_2 = 1.0$ and $L_3 = 5.0$ we get |
* after the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(2.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.4559) = 0.984\hspace{0.05cm},$ | * after the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(2.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.4559) = 0.984\hspace{0.05cm},$ | ||
| + | |||
* according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}5.0 \big ) = 1.000 \hspace{0.05cm}.$ | * according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}5.0 \big ) = 1.000 \hspace{0.05cm}.$ | ||
| Line 74: | Line 81: | ||
'''(2)''' On the other hand one obtains for $L_2 = L_3 = 1.0$ | '''(2)''' On the other hand one obtains for $L_2 = L_3 = 1.0$ | ||
* according to the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(0.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.2135) = 0.433\hspace{0.05cm},$ | * according to the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(0.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.2135) = 0.433\hspace{0.05cm},$ | ||
| + | |||
* according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}1.0 \big ) = 1.000 \hspace{0.05cm}.$ | * according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}1.0 \big ) = 1.000 \hspace{0.05cm}.$ | ||
| − | One can see the clear discrepancy between the two approaches. The second approach (approximation) is clearly more positive than the first (correct) approach. However, it is actually only important that the iterations lead to the desired decoding result. | + | One can see the clear discrepancy between the two approaches. The second approach $($approximation$)$ is clearly more positive than the first $($correct$)$ approach. However, it is actually only important that the iterations lead to the desired decoding result. |
| Line 83: | Line 91: | ||
| − | Hints: | + | <u>Hints:</u> |
*The exercise belongs to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder|"Soft–in Soft–out Decoder"]]. | *The exercise belongs to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder|"Soft–in Soft–out Decoder"]]. | ||
| − | *Referred to in particular [[Channel_Coding/Soft-in_Soft-Out_Decoder# | + | |
| − | * Only the '''second solution approach''' is treated here. | + | *Referred to in particular [[Channel_Coding/Soft-in_Soft-Out_Decoder#Calculation_of_extrinsic_log_likelihood_ratios|"Calculation of extrinsic log likelihood ratios"]]. |
| − | * For the first solution approach we refer to | + | |
| + | * Only the '''second solution approach''' is treated here. | ||
| + | |||
| + | * For the first solution approach we refer to [[Aufgaben:Exercise_4.5Z:_Tangent_Hyperbolic_and_Inverse|$\text{Exercise 4.5Z}$]] . | ||
| Line 94: | Line 105: | ||
===Questions=== | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {It holds $\underline{L} = (+1.0, +0.4, -1.0)$. Determine the extrinsic $L$–values according to the '''second $L_{\rm E}(i)$–approach''' without previous iteration $\underline{(I = 0)}$. | + | {It holds $\underline{L} = (+1.0, +0.4, -1.0)$. Determine the extrinsic $L$–values according to the '''second $L_{\rm E}(i)$–approach''' without previous iteration $\underline{(I = 0)}$. |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(1) \ = \ ${ -0.412--0.388 } | $L_{\rm E}(1) \ = \ ${ -0.412--0.388 } | ||
| Line 100: | Line 111: | ||
$L_{\rm E}(3) \ = \ ${ 0.4 3% } | $L_{\rm E}(3) \ = \ ${ 0.4 3% } | ||
| − | {What are the a posteriori–$ | + | {What are the a-posteriori $L$–values $L_i = L_{\rm APP} (i)$ for the first iteration $\underline{(I = 1)}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $L_1 \ = \ ${ 0.6 3% } |
| − | $ | + | $L_2 \ = \ ${ -0.618--0.582 } |
| − | $ | + | $L_3 \ = \ ${ -0.618--0.582 } |
{Which of the following statements are true for $\underline{L} = (+1.0, +0.4, -1.0)$? | {Which of the following statements are true for $\underline{L} = (+1.0, +0.4, -1.0)$? | ||
|type="[]"} | |type="[]"} | ||
| − | + | + | + Hard decision after $I = 1$ leads to the code word $\underline{x}_1 = (+1, -1, -1)$. |
+ This does not change after further iterations. | + This does not change after further iterations. | ||
- Further iterations do not increase the reliability for $\underline{x}_1$ . | - Further iterations do not increase the reliability for $\underline{x}_1$ . | ||
| Line 116: | Line 127: | ||
+ The iterative decoding leads to the result $\underline{x}_0 = (+1, +1, +1)$. | + The iterative decoding leads to the result $\underline{x}_0 = (+1, +1, +1)$. | ||
- The iterative decoding leads to the result $\underline{x}_2 = (-1, +1, -1)$. | - The iterative decoding leads to the result $\underline{x}_2 = (-1, +1, -1)$. | ||
| − | + | + | + Hard decision also returns this result for $I \ge 1$. |
{Which of the following statements are true for $\underline{L} = (+0.6, +1.0, -0.8)$? | {Which of the following statements are true for $\underline{L} = (+0.6, +1.0, -0.8)$? | ||
|type="[]"} | |type="[]"} | ||
| − | - The iterative decoding | + | - The iterative decoding leads to the result $\underline{x}_0 = (+1, +1, +1)$. |
+ The iterative decoding leads to the result $\underline{x}_2 = (-1, +1, -1)$. | + The iterative decoding leads to the result $\underline{x}_2 = (-1, +1, -1)$. | ||
| − | + | + | + Hard decision also returns this result for $I \ge 1$. |
{Which of the following statements are true for $\underline{L} = (+0.6, +1.0, -0.6)$? | {Which of the following statements are true for $\underline{L} = (+0.6, +1.0, -0.6)$? | ||
| Line 134: | Line 145: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
[[File:P_ID3027__KC_A_4_5a_v2.png|right|frame|Results for $\underline{L}=(+1.0, +0.4, –1.0)$]] | [[File:P_ID3027__KC_A_4_5a_v2.png|right|frame|Results for $\underline{L}=(+1.0, +0.4, –1.0)$]] | ||
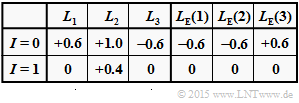
| − | '''(1)''' According to the second $L_{\rm E}(i)$ approach holds: | + | '''(1)''' According to the second $L_{\rm E}(i)$ approach holds: |
:$${\rm sign} [L_{\rm E}(1)] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} [L_{\rm E}(2)] \cdot {\rm sign} [L_{\rm E}(3)] = -1 \hspace{0.05cm},$$ | :$${\rm sign} [L_{\rm E}(1)] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} [L_{\rm E}(2)] \cdot {\rm sign} [L_{\rm E}(3)] = -1 \hspace{0.05cm},$$ | ||
| − | :$$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) = {\rm Min} \left ( 0.4\hspace{0.05cm}, \hspace{0.05cm}1.0 \right ) = 0.4 | + | :$$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) = {\rm Min} \left ( 0.4\hspace{0.05cm}, \hspace{0.05cm}1.0 \right ) = 0.4$$ |
| − | \Rightarrow \hspace{0.3cm}L_{\rm E}(1) \hspace{0.15cm} \underline{-0.4}\hspace{0.05cm}.$$ | + | :$$\Rightarrow \hspace{0.3cm}L_{\rm E}(1) \hspace{0.15cm} \underline{-0.4}\hspace{0.05cm}.$$ |
*In the same way you get: | *In the same way you get: | ||
| − | :$$L_{\rm E}(2) \hspace{0.15cm} \underline{-1.0}\hspace{0.05cm}, | + | :$$L_{\rm E}(2) \hspace{0.15cm} \underline{-1.0}\hspace{0.05cm}, $$ |
| − | L_{\rm E}(3) \hspace{0.15cm} \underline{+0.4}\hspace{0.05cm}.$$ | + | :$$L_{\rm E}(3) \hspace{0.15cm} \underline{+0.4}\hspace{0.05cm}.$$ |
| − | '''(2)''' The a posteriori $L$ values at the beginning of the first iteration $(I = 1)$ are the sum of the previous $L$–values (for $I = 0$) and the extrinsic values calculated in (1): | + | '''(2)''' The a-posteriori $L$–values at the beginning of the first iteration $(I = 1)$ are the sum |
| + | *of the previous $L$–values $($for $I = 0$) | ||
| + | *and the extrinsic values calculated in subtask '''(1)''': | ||
:$$L_1 = L_{\rm APP}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1.0 + (-0.4)\hspace{0.15cm} \underline{=+0.6}\hspace{0.05cm},$$ | :$$L_1 = L_{\rm APP}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1.0 + (-0.4)\hspace{0.15cm} \underline{=+0.6}\hspace{0.05cm},$$ | ||
:$$L_2 = L_{\rm APP}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.4 + (-1.0)\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm},$$ | :$$L_2 = L_{\rm APP}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.4 + (-1.0)\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm},$$ | ||
| Line 150: | Line 163: | ||
| − | '''(3)''' As can be seen from the above table, <u>solutions 1 and 2</u> are correct in contrast to answer 3: | + | '''(3)''' As can be seen from the above table, the <u>solutions 1 and 2</u> are correct in contrast to answer 3: |
| − | *With each new iteration, the | + | *With each new iteration, the magnitudes of $L(1), \ L(2)$ and $L(3)$ become significantly larger. |
| − | + | [[File:P_ID3030__KC_A_4_5d_v2.png|right|frame|Results for $\underline{L}=(+0.6, +1.0, –0.4)$]] | |
| − | '''(4)''' As can be seen from the adjacent table, <u>answers 1 and 3</u> are correct: | + | <br><br> |
| − | *So the decision is made for the code word $\underline{x}_0 = (+1, +1, +1)$. | + | '''(4)''' As can be seen from the adjacent table, |
| − | *From $I = 1$ this would also be the decision of | + | the <u>answers 1 and 3</u> are correct: |
| + | *So the decision is made for the code word $\underline{x}_0 = (+1, +1, +1)$. | ||
| + | |||
| + | *From $I = 1$ this would also be the decision of "hard decision". | ||
<br clear=all> | <br clear=all> | ||
[[File:P_ID3028__KC_A_4_5e_v2.png|right|frame|Results for $\underline{L}=(+0.6, +1.0, –0.8)$]] | [[File:P_ID3028__KC_A_4_5e_v2.png|right|frame|Results for $\underline{L}=(+0.6, +1.0, –0.8)$]] | ||
| − | '''(5)''' Correct are <u>answers 2 and 3</u>: | + | '''(5)''' Correct are the <u>answers 2 and 3</u>: |
| − | *Because $|L(3)| > |L(1)|$ the following is valid | + | *Because of $|L(3)| > |L(1)|$ the following is valid for $I /ge 1$: $L_1 < 0 \hspace{0.05cm},\hspace{0.2cm} |
L_2 > 0 \hspace{0.05cm},\hspace{0.2cm} | L_2 > 0 \hspace{0.05cm},\hspace{0.2cm} | ||
L_3 < 0 \hspace{0.05cm}.$ | L_3 < 0 \hspace{0.05cm}.$ | ||
| − | *From this iteration loop, | + | |
| + | *From this iteration loop, hard decision returns the code word $\underline{x}_2 = (-1, +1, -1)$. | ||
<br clear=all> | <br clear=all> | ||
[[File: P_ID3029__KC_A_4_5f_v1.png|right|frame|Results for $\underline{L}=(+0.6, +1.0, –0.6)$]] | [[File: P_ID3029__KC_A_4_5f_v1.png|right|frame|Results for $\underline{L}=(+0.6, +1.0, –0.6)$]] | ||
| − | '''(6)''' Correct is the <u>proposed solution 3</u>: | + | '''(6)''' Correct is the <u>proposed solution 3</u>: |
| − | *The adjacent table shows that under the condition $|L(1)| = |L(3)|$, starting from the iteration loop $I = 1$, all extrinsic $L$–values are zero. | + | *The adjacent table shows that under the condition $|L(1)| = |L(3)|$, starting from the iteration loop $I = 1$, all extrinsic $L$–values are zero. |
| − | *Thus, the a posteriori $L$ values remain constantly equal to $\underline{L} = (0., +0.4, 0.)$ even for $I > 1$, which cannot be assigned to any code word. | + | |
| + | *Thus, the a-posteriori $L$– values remain constantly equal to $\underline{L} = (0., +0.4, 0.)$ even for $I > 1$, which cannot be assigned to any code word. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 17:06, 4 December 2022
We assume as in the "theory section" the "single parity–check code" $\rm SPC \, (3, \, 2, \, 2)$.
The possible code words are $\underline{x} \hspace{-0.01cm}\in \hspace{-0.01cm} \{ \underline{x}_0,\hspace{0.05cm} \underline{x}_1,\hspace{0.05cm} \underline{x}_2,\hspace{0.05cm} \underline{x}_3\}$ with
- $$\underline{x}_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm},$$
- $$\underline{x}_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} \underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$
- $$\underline{x}_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} \underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$
- $$\underline{x}_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm resp. } \hspace{0.35cm} \underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm}.$$
In the exercise we mostly use the second (bipolar) representation of the code symbols:
- $$x_i ∈ \{+1, -1\}.$$
Note:
- It is not that the $\rm SPC \, (3, \, 2, \, 2)$ would be of much practical interest, since, for example, in "hard decision" because of $d_{\rm min} = 2$ only one error can be detected and none can be corrected.
- However, the code is well suited for demonstration purposes because of the manageable effort involved.
- With "iterative symbol-wise decoding" one can also correct one error.
- In the present code, the extrinsic $L$–values $\underline{L}_{\rm E} = \big (L_{\rm E}(1), \ L_{\rm E}(2), \ L_{\rm E}(3)\big )$ must be calculated according to the following equation:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} \right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} \hspace{0.05cm}\right ]}.$$
- Here $\underline{x}^{(-1)}$ denotes all symbols except $x_i$ and is thus a vector of length $n - 1 = 2$.
⇒ As the »first $L_{\rm E}(i)$ approach« we refer to the approach corresponding to the equations
- $$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$
- $$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$
- $$L_{\rm E}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \right ] \hspace{0.05cm}.$$
(1) This $L_{\rm E}(i)$ approach underlies the results table above $($red entries$)$, assuming the following a-posteriori $L$–values:
- $$\underline {L}_{\rm APP} = (+1.0\hspace{0.05cm},\hspace{0.05cm}+0.4\hspace{0.05cm},\hspace{0.05cm}-1.0) \hspace{0.5cm}\Rightarrow \hspace{0.5cm} L_1 = +1.0\hspace{0.05cm},\hspace{0.15cm} L_2 = +0.4\hspace{0.05cm},\hspace{0.15cm} L_3 = -1.0\hspace{0.05cm}.$$
(2) The extrinsic $L$–values for the zeroth iteration result in $($derivation in $\text{Exercise 4.5Z})$:
- $$L_{\rm E}(1) = -0.1829, \ L_{\rm E}(2) = -0.4337, \ L_{\rm E}(3) = +0.1829.$$
(3) The a-posteriori $L$–values at the beginning of the first iteration are thus
- $$\underline{L_{\rm APP} }^{(I=1)} = \underline{L_{\rm APP} }^{(I=0)} + \underline{L}_{\hspace{0.02cm}\rm E}^{(I=0)} = (+0.8171\hspace{0.05cm},\hspace{0.05cm}-0.0337\hspace{0.05cm},\hspace{0.05cm}-0.8171) \hspace{0.05cm} . $$
(4) From this, the new extrinsic $L$–values for the iteration loop $I = 1$ are as follows:
- $$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(-0.0337/2) \cdot {\rm tanh}(-0.8171/2) \big ] = 0.0130 = -L_{\rm E}(3)\hspace{0.05cm},$$
- $$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(+0.8171/2) \cdot {\rm tanh}(-0.8171/2) \big ] = - 0.3023\hspace{0.05cm}.$$
Further, one can see from the above table:
- A hard decision according to the signs before the first iteration $(I = 0)$ fails, since $(+1, +1, -1)$ is not a valid $\rm SPC \, (3, \, 2, \, 2)$ code word.
- But already after $I = 1$ iterations, a hard decision yields a valid code word, namely $\underline{x}_2 = (+1, -1, -1)$.
- Also in later graphs, the rows with correct hard decisions for the first time are highlighted in blue.
- Hard decisions after further iterations $(I ≥ 2)$ each lead to the same code word $\underline{x}_2$. This statement is not only valid for this example, but in general.
Besides, in this exercise we consider a »second $L_{\rm E}(i)$ approach«, which is given here for the example of the first symbol $(i = 1)$:
- $${\rm sign} \big[L_{\rm E}(1)\big] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} \big[L_{\rm E}(2)\big] \cdot {\rm sign} \big[L_{\rm E}(3)\big]\hspace{0.05cm},$$
- $$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) \hspace{0.05cm}.$$
This second approach is based on the assumption that the reliability of $L_{\rm E}(i)$ is essentially determined by the most unreliable neighbor symbol. The better $($larger$)$ the input log likelihood ratio is completely disregarded.
Let us consider two examples for this:
(1) For $L_2 = 1.0$ and $L_3 = 5.0$ we get
- after the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(2.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.4559) = 0.984\hspace{0.05cm},$
- according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}5.0 \big ) = 1.000 \hspace{0.05cm}.$
(2) On the other hand one obtains for $L_2 = L_3 = 1.0$
- according to the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(0.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.2135) = 0.433\hspace{0.05cm},$
- according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}1.0 \big ) = 1.000 \hspace{0.05cm}.$
One can see the clear discrepancy between the two approaches. The second approach $($approximation$)$ is clearly more positive than the first $($correct$)$ approach. However, it is actually only important that the iterations lead to the desired decoding result.
Hints:
- The exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Referred to in particular "Calculation of extrinsic log likelihood ratios".
- Only the second solution approach is treated here.
- For the first solution approach we refer to $\text{Exercise 4.5Z}$ .
Questions
Solution
(1) According to the second $L_{\rm E}(i)$ approach holds:
- $${\rm sign} [L_{\rm E}(1)] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} [L_{\rm E}(2)] \cdot {\rm sign} [L_{\rm E}(3)] = -1 \hspace{0.05cm},$$
- $$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) = {\rm Min} \left ( 0.4\hspace{0.05cm}, \hspace{0.05cm}1.0 \right ) = 0.4$$
- $$\Rightarrow \hspace{0.3cm}L_{\rm E}(1) \hspace{0.15cm} \underline{-0.4}\hspace{0.05cm}.$$
- In the same way you get:
- $$L_{\rm E}(2) \hspace{0.15cm} \underline{-1.0}\hspace{0.05cm}, $$
- $$L_{\rm E}(3) \hspace{0.15cm} \underline{+0.4}\hspace{0.05cm}.$$
(2) The a-posteriori $L$–values at the beginning of the first iteration $(I = 1)$ are the sum
- of the previous $L$–values $($for $I = 0$)
- and the extrinsic values calculated in subtask (1):
- $$L_1 = L_{\rm APP}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1.0 + (-0.4)\hspace{0.15cm} \underline{=+0.6}\hspace{0.05cm},$$
- $$L_2 = L_{\rm APP}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.4 + (-1.0)\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm},$$
- $$L_3 = L_{\rm APP}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (-1.0) + 0.4\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm}.$$
(3) As can be seen from the above table, the solutions 1 and 2 are correct in contrast to answer 3:
- With each new iteration, the magnitudes of $L(1), \ L(2)$ and $L(3)$ become significantly larger.
(4) As can be seen from the adjacent table,
the answers 1 and 3 are correct:
- So the decision is made for the code word $\underline{x}_0 = (+1, +1, +1)$.
- From $I = 1$ this would also be the decision of "hard decision".
(5) Correct are the answers 2 and 3:
- Because of $|L(3)| > |L(1)|$ the following is valid for $I /ge 1$: $L_1 < 0 \hspace{0.05cm},\hspace{0.2cm} L_2 > 0 \hspace{0.05cm},\hspace{0.2cm} L_3 < 0 \hspace{0.05cm}.$
- From this iteration loop, hard decision returns the code word $\underline{x}_2 = (-1, +1, -1)$.
(6) Correct is the proposed solution 3:
- The adjacent table shows that under the condition $|L(1)| = |L(3)|$, starting from the iteration loop $I = 1$, all extrinsic $L$–values are zero.
- Thus, the a-posteriori $L$– values remain constantly equal to $\underline{L} = (0., +0.4, 0.)$ even for $I > 1$, which cannot be assigned to any code word.