Difference between revisions of "Aufgaben:Exercise 4.6: Locality Curve for SSB-AM"
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite=Signal_Representation/ | + | {{quiz-Header|Buchseite=Signal_Representation/Equivalent Low-Pass Signal and its Spectral Function |
}} | }} | ||
| − | [[File:P_ID764__Sig_A_4_6.png|250px|right|frame| | + | [[File:P_ID764__Sig_A_4_6.png|250px|right|frame|Spectrum of the analytical signal]] |
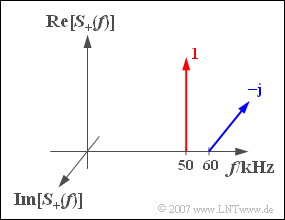
We consider the analytical signal $s_+(t)$ with the spectral function | We consider the analytical signal $s_+(t)$ with the spectral function | ||
| Line 12: | Line 12: | ||
Here $f_{50}$ and $f_{60}$ are abbreviations for the frequencies $50 \ \rm kHz$ and $60 \ \rm kHz$ respectively. | Here $f_{50}$ and $f_{60}$ are abbreviations for the frequencies $50 \ \rm kHz$ and $60 \ \rm kHz$ respectively. | ||
| − | In this task, the course of the equivalent low-pass signal $s_{\rm TP}(t)$ | + | In this task, the course of the equivalent low-pass signal $s_{\rm TP}(t)$ is computed. This course is also referred to as the "Locality Curve" in this tutorial. |
| − | *In | + | *In subtasks '''(1)''' to '''(3)''', we assume that the signal $s(t)$ is produced by a single-sideband amplitude modulation of the sinusoidal source signal of frequency $f_{\rm N} = 10 \ \text{ kHz}$ with a cosinusoidal carrier at $f_{\rm T} = f_{50}$, whereby only the upper sideband is transmitted ⇒ $\text{Upper Sideband Modulation}$. |
| − | * | + | *In contrast, subtask '''(4)''' assumes the carrier frequency $f_{\rm T} = f_{60}$ . This assumption presupposes that $\text{Lower Sideband Modulation}$ has taken place. |
| Line 21: | Line 21: | ||
| + | ''Hints:'' | ||
| + | *This exercise belongs to the chapter [[Signal_Representation/Equivalent_Low-Pass_Signal_and_its_Spectral_Function|Equivalent Low-Pass Signal and its Spectral Function]]. | ||
| + | |||
| + | *You can check your solution with the interactive applet [[Applets:Physical_Signal_%26_Equivalent_Lowpass_Signal|Physical Signal & Equivalent Low-Pass Signal]] ⇒ "Locality Curve". | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Questions=== | |
| − | === | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Give the equivalent low-pass signal $s_{\rm TP}(t)$ for the carrier frequency $f_{\rm T} = 50 \ \text{ kHz}$. Which of the following statements are true? |
|type="()"} | |type="()"} | ||
| − | - | + | - The locality curve describes an ellipse. |
| − | + | + | + The locality curve describes a circle. |
| − | - | + | - The localitycurve describes an arc. |
| − | { | + | {Calculate the magnitude function $a(t) = |s_{\rm TP}(t)|$. What is the value of $a_0$ at $t = 0$ and the minimum and maximum values of the magnitude? |
|type="{}"} | |type="{}"} | ||
$a_{\text{min}}\ = \ $ { 0. } | $a_{\text{min}}\ = \ $ { 0. } | ||
| Line 45: | Line 44: | ||
| − | { | + | {Calculate the phase function $\phi(t)$. What are the phase values at $t = 0$ and $t=25 \ {\rm µ} \text{s}$? <br>Interpret $\phi (t)$ in the range around $t=75 \ {\rm µ} \text{s}$. |
|type="{}"} | |type="{}"} | ||
| − | $\phi(t=0 \ {\rm µ} \text{s})\ = \ $ { -46--44 } $\text{ | + | $\phi(t=0 \ {\rm µ} \text{s})\ = \ $ { -46--44 } $\text{deg}$ |
| − | $\phi(t=25 \ {\rm µ} \text{s})\ = \ $ { 0. } $\text{ | + | $\phi(t=25 \ {\rm µ} \text{s})\ = \ $ { 0. } $\text{deg}$ |
| − | $\phi(t=75 \ {\rm µ} \text{s})\ = \ $ { 0. } $\text{ | + | $\phi(t=75 \ {\rm µ} \text{s})\ = \ $ { 0. } $\text{deg}$ |
| − | { | + | {Give the equivalent low-pass signal $s_{\rm TP}(t)$ for $f_{\rm T} = 60 \ \text{kHz} = f_{60}$. Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The locality curve is a circle with radius $1$ around the centre $(0, –{\rm j})$ . |
| − | - | + | - Now $s_{\rm TP}(t = 0) = 1 + {\rm j}$ applies. |
| − | + | + | + The magnitude function $a(t)$ is unchanged compared to $f_{\rm T} = f_{50}$ . |
| − | - | + | - The phase function $\phi (t)$ is unchanged compared to $f_{\rm T} = f_{50}$ . |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[File:P_ID766__Sig_A_4_6_a.png|250px|right|frame| | + | [[File:P_ID766__Sig_A_4_6_a.png|250px|right|frame|Locality curve for <br>Upper Sideband Modulation]] |
| − | '''(1)''' | + | '''(1)''' The <u>proposed solution 2</u> is correct: |
| − | * | + | *The spectrum of the equivalent low-pass signal with carrier frequency $f_{\rm T} = f_{50} = 50 \ \text{kHz}$: |
:$$S_{\rm TP}(f ) = S_{\rm +}(f+ f_{\rm 50}) = 1 \cdot \delta (f)- | :$$S_{\rm TP}(f ) = S_{\rm +}(f+ f_{\rm 50}) = 1 \cdot \delta (f)- | ||
{\rm j} \cdot \delta (f - f_{\rm 10}) .$$ | {\rm j} \cdot \delta (f - f_{\rm 10}) .$$ | ||
| − | * | + | *This gives for the associated time signal: |
:$$s_{\rm TP}(t) = {\rm 1 } - {\rm j} \cdot {\rm e}^{{\rm | :$$s_{\rm TP}(t) = {\rm 1 } - {\rm j} \cdot {\rm e}^{{\rm | ||
j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }.$$ | j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }.$$ | ||
| − | * | + | *Starting from the point $(1, –{\rm j})$ ⇒ $s_{\rm TP}(t)$ runs on a circle with centre $(1, 0)$ and radius $1$. |
| − | * | + | *The period duration is equal to the reciprocal of the frequency: $T_0 = 1/f_{10} = 100 \ µ \text{s}$. |
| − | '''(2)''' | + | '''(2)''' Splitting the above equation into real and imaginary parts, we get: |
:$$s_{\rm TP}(t) = {\rm 1 } + \sin({ \omega_{\rm 10} \hspace{0.05cm} t }) | :$$s_{\rm TP}(t) = {\rm 1 } + \sin({ \omega_{\rm 10} \hspace{0.05cm} t }) | ||
-{\rm j}\cdot \cos({ \omega_{\rm 10} \hspace{0.05cm} t }).$$ | -{\rm j}\cdot \cos({ \omega_{\rm 10} \hspace{0.05cm} t }).$$ | ||
| − | * | + | *This leads to the magnitude function |
:$$a(t)= |s_{\rm TP}(t)|=\sqrt{{\rm Re}\left[s_{\rm | :$$a(t)= |s_{\rm TP}(t)|=\sqrt{{\rm Re}\left[s_{\rm | ||
| Line 90: | Line 89: | ||
= \sqrt{2 \cdot ( 1 + \sin(\omega_{\rm 10}\hspace{0.05cm} t))}.$$ | = \sqrt{2 \cdot ( 1 + \sin(\omega_{\rm 10}\hspace{0.05cm} t))}.$$ | ||
| − | * | + | *For the minimum value, considering $\sin(\omega_{10} \cdot t) \geq -1$ ⇒ $a_{\text{min}} \; \underline{= 0}$. |
| − | * | + | *The maximum value is obtained from $\sin(\omega_{10} \cdot t \leq 1$ ) ⇒ $a_{\text{max}} \; \underline{= 2}$. |
| − | * | + | *At $t = 0$ , the magnitude is equal to $a_0 = \sqrt{2 }\; \underline{\approx 1.414}$. |
| − | '''(3)''' | + | '''(3)''' According to the general definition: |
:$$\phi(t)= {\rm arctan} \hspace{0.1cm}\frac{{\rm Im}\left[s_{\rm | :$$\phi(t)= {\rm arctan} \hspace{0.1cm}\frac{{\rm Im}\left[s_{\rm | ||
| Line 103: | Line 102: | ||
\sin(\omega_{\rm 10}\hspace{0.05cm} t)}.$$ | \sin(\omega_{\rm 10}\hspace{0.05cm} t)}.$$ | ||
| − | * | + | *For $t = 0$ ⇒ $\cos( \omega_{10} \cdot t ) = 1$ and $\sin( \omega_{10} \cdot t ) = 0$. It follows: |
:$$\phi(t = 0)= {\rm arctan} (-1) \hspace{0.15 cm}\underline{= -45^\circ}.$$ | :$$\phi(t = 0)= {\rm arctan} (-1) \hspace{0.15 cm}\underline{= -45^\circ}.$$ | ||
| − | * | + | *On the other hand, for $t = T_0/4 =25 \ µ \text{s}$: |
:$$\cos(\omega_{\rm 10}\hspace{0.05cm} t) = 0; | :$$\cos(\omega_{\rm 10}\hspace{0.05cm} t) = 0; | ||
| Line 114: | Line 113: | ||
\hspace{0.05cm} µ s}) \hspace{0.15 cm}\underline{= 0}.$$ | \hspace{0.05cm} µ s}) \hspace{0.15 cm}\underline{= 0}.$$ | ||
| − | * | + | *The two angles calculated so far can also be read from the graph above. |
| − | + | The phase value at $t =75 \ µ \text{s}$, on the other hand, must be determined by boundary crossing, since here both the real and imaginary parts become zero and thus the argument of the arctan function is indeterminate. One obtains $\phi(t=75 \ µ \text{s}) \; \underline{= 0}.$ This result is to be verified numerically here: | |
| − | * | + | *If one calculates the phase function for $t =74 \ {\rm µ} \text{s}$, one obtains with $\omega_{10} \cdot t = 1.48 \cdot \pi \; \Rightarrow \; 266.4^\circ$: |
:$$\phi(t = {\rm 74 \hspace{0.05cm} {\rm µ} s})= {\rm arctan} | :$$\phi(t = {\rm 74 \hspace{0.05cm} {\rm µ} s})= {\rm arctan} | ||
| Line 125: | Line 124: | ||
arctan}(31)\approx 88^\circ.$$ | arctan}(31)\approx 88^\circ.$$ | ||
| − | * | + | *Accordingly, for $t =76 \ {\rm µ} \text{s}$ with $\omega_{10} \cdot t = 1.52 \cdot \pi \; \Rightarrow \; 273.6^\circ$ : |
:$$\phi(t = {\rm 76 \hspace{0.05cm} {\rm µ} s})= {\rm arctan} | :$$\phi(t = {\rm 76 \hspace{0.05cm} {\rm µ} s})= {\rm arctan} | ||
| Line 131: | Line 130: | ||
\approx {\rm arctan}(-31)\approx -88^\circ.$$ | \approx {\rm arctan}(-31)\approx -88^\circ.$$ | ||
| − | * | + | *The numerical values suggest that the limit values for $t \; \rightarrow \; 75 \ {\rm µ} \text{s}$ result in $\pm 90^\circ$ depending on whether this value is approached from above or below. |
| − | * | + | *The phase value at exactly $t =75 \ {\rm µ} \text{s}$ is equal to the mean value between the right-hand and left-hand limit values, i.e. actually zero. |
| − | [[File:P_ID767__Sig_A_4_6_d.png|250px|right|frame| | + | [[File:P_ID767__Sig_A_4_6_d.png|250px|right|frame|Locality curve for <br>Lower Sideband Modulation]] |
| − | '''(4)''' | + | '''(4)''' <u>The first and third suggested solutions</u> are correct: |
| + | *With the carrier frequency $f_{\rm T} = f_{60} = 60 \ \text{ kHz}$ the equations for frequency and time domain are: | ||
:$$S_{\rm TP}(f ) = S_{\rm +}(f+ f_{\rm 60}) = -{\rm j} \cdot \delta | :$$S_{\rm TP}(f ) = S_{\rm +}(f+ f_{\rm 60}) = -{\rm j} \cdot \delta | ||
| Line 144: | Line 144: | ||
j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }.$$ | j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }.$$ | ||
| − | In | + | In the graph, $s_{\rm TP}(t)$ is shown. It can be seen: |
| − | * | + | *The locality curve is again a circle with radius $1$, but now with centre $(0, –{\rm j})$. |
| − | * | + | *Here, too: $s_{\rm TP}(t = 0) = 1 - {\rm j}$. |
| − | * | + | *You now move clockwise on the locality curve. |
| − | * | + | *The period continues to be $T_0 = 1/f_{10} = 100 \ µ \text{s}$. |
| − | * | + | *The locality curve is now rotated by $90^\circ$ in the complex plane compared to sub-task '''(1)'''. |
| − | * | + | *For all times, the same pointer lengths result as for $f_{\rm T} = f_{50}$. The magnitude remains the same. |
| − | * | + | *The phase function $\phi(t)$ now yields values between $-\pi$ and zero, while the phase function calculated in subtask '''(3)''' has assumed values between $\pm \pi/2$. |
| − | + | *It is valid for all times $t$: $\phi_{\rm subtask \ (4)}= -(\phi_{\rm subtask \ (3)} + 90^\circ).$ | |
| − | + | ||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^4.3 Equivalent LP Signal and its Spectral Function^]] |
Latest revision as of 15:01, 24 May 2021
We consider the analytical signal $s_+(t)$ with the spectral function
- $$S_{\rm +}(f) = 1 \cdot \delta (f - f_{\rm 50})- {\rm j} \cdot \delta (f - f_{\rm 60}) .$$
Here $f_{50}$ and $f_{60}$ are abbreviations for the frequencies $50 \ \rm kHz$ and $60 \ \rm kHz$ respectively.
In this task, the course of the equivalent low-pass signal $s_{\rm TP}(t)$ is computed. This course is also referred to as the "Locality Curve" in this tutorial.
- In subtasks (1) to (3), we assume that the signal $s(t)$ is produced by a single-sideband amplitude modulation of the sinusoidal source signal of frequency $f_{\rm N} = 10 \ \text{ kHz}$ with a cosinusoidal carrier at $f_{\rm T} = f_{50}$, whereby only the upper sideband is transmitted ⇒ $\text{Upper Sideband Modulation}$.
- In contrast, subtask (4) assumes the carrier frequency $f_{\rm T} = f_{60}$ . This assumption presupposes that $\text{Lower Sideband Modulation}$ has taken place.
Hints:
- This exercise belongs to the chapter Equivalent Low-Pass Signal and its Spectral Function.
- You can check your solution with the interactive applet Physical Signal & Equivalent Low-Pass Signal ⇒ "Locality Curve".
Questions
Solution
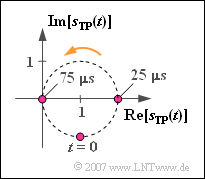
(1) The proposed solution 2 is correct:
- The spectrum of the equivalent low-pass signal with carrier frequency $f_{\rm T} = f_{50} = 50 \ \text{kHz}$:
- $$S_{\rm TP}(f ) = S_{\rm +}(f+ f_{\rm 50}) = 1 \cdot \delta (f)- {\rm j} \cdot \delta (f - f_{\rm 10}) .$$
- This gives for the associated time signal:
- $$s_{\rm TP}(t) = {\rm 1 } - {\rm j} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }.$$
- Starting from the point $(1, –{\rm j})$ ⇒ $s_{\rm TP}(t)$ runs on a circle with centre $(1, 0)$ and radius $1$.
- The period duration is equal to the reciprocal of the frequency: $T_0 = 1/f_{10} = 100 \ µ \text{s}$.
(2) Splitting the above equation into real and imaginary parts, we get:
- $$s_{\rm TP}(t) = {\rm 1 } + \sin({ \omega_{\rm 10} \hspace{0.05cm} t }) -{\rm j}\cdot \cos({ \omega_{\rm 10} \hspace{0.05cm} t }).$$
- This leads to the magnitude function
- $$a(t)= |s_{\rm TP}(t)|=\sqrt{{\rm Re}\left[s_{\rm TP}(t)\right]^2 + {\rm Im}\left[s_{\rm TP}(t)\right]^2 }= \sqrt{1 + 2 \sin(\omega_{\rm 10}\hspace{0.05cm} t)+ \sin^2(\omega_{\rm 10}\hspace{0.05cm} t)+ \cos^2(\omega_{\rm 10}\hspace{0.05cm} t)} = \sqrt{2 \cdot ( 1 + \sin(\omega_{\rm 10}\hspace{0.05cm} t))}.$$
- For the minimum value, considering $\sin(\omega_{10} \cdot t) \geq -1$ ⇒ $a_{\text{min}} \; \underline{= 0}$.
- The maximum value is obtained from $\sin(\omega_{10} \cdot t \leq 1$ ) ⇒ $a_{\text{max}} \; \underline{= 2}$.
- At $t = 0$ , the magnitude is equal to $a_0 = \sqrt{2 }\; \underline{\approx 1.414}$.
(3) According to the general definition:
- $$\phi(t)= {\rm arctan} \hspace{0.1cm}\frac{{\rm Im}\left[s_{\rm TP}(t)\right]}{{\rm Re}\left[s_{\rm TP}(t)\right]}= {\rm arctan} \hspace{0.1cm}\frac{-\cos(\omega_{\rm 10}\hspace{0.05cm} t)}{1 + \sin(\omega_{\rm 10}\hspace{0.05cm} t)}.$$
- For $t = 0$ ⇒ $\cos( \omega_{10} \cdot t ) = 1$ and $\sin( \omega_{10} \cdot t ) = 0$. It follows:
- $$\phi(t = 0)= {\rm arctan} (-1) \hspace{0.15 cm}\underline{= -45^\circ}.$$
- On the other hand, for $t = T_0/4 =25 \ µ \text{s}$:
- $$\cos(\omega_{\rm 10}\hspace{0.05cm} t) = 0; \hspace{0.2cm}\sin(\omega_{\rm 10}\hspace{0.05cm} t) = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi(t = {\rm 25 \hspace{0.05cm} µ s}) \hspace{0.15 cm}\underline{= 0}.$$
- The two angles calculated so far can also be read from the graph above.
The phase value at $t =75 \ µ \text{s}$, on the other hand, must be determined by boundary crossing, since here both the real and imaginary parts become zero and thus the argument of the arctan function is indeterminate. One obtains $\phi(t=75 \ µ \text{s}) \; \underline{= 0}.$ This result is to be verified numerically here:
- If one calculates the phase function for $t =74 \ {\rm µ} \text{s}$, one obtains with $\omega_{10} \cdot t = 1.48 \cdot \pi \; \Rightarrow \; 266.4^\circ$:
- $$\phi(t = {\rm 74 \hspace{0.05cm} {\rm µ} s})= {\rm arctan} \hspace{0.1cm}\frac{\cos(86.4^\circ)}{1 - \sin(86.4^\circ)} = {\rm arctan} \hspace{0.1cm}\frac{0.062}{1 - 0.998} \approx {\rm arctan}(31)\approx 88^\circ.$$
- Accordingly, for $t =76 \ {\rm µ} \text{s}$ with $\omega_{10} \cdot t = 1.52 \cdot \pi \; \Rightarrow \; 273.6^\circ$ :
- $$\phi(t = {\rm 76 \hspace{0.05cm} {\rm µ} s})= {\rm arctan} \hspace{0.1cm}\frac{-\cos(86.4^\circ)}{1 - \sin(86.4^\circ)} \approx {\rm arctan}(-31)\approx -88^\circ.$$
- The numerical values suggest that the limit values for $t \; \rightarrow \; 75 \ {\rm µ} \text{s}$ result in $\pm 90^\circ$ depending on whether this value is approached from above or below.
- The phase value at exactly $t =75 \ {\rm µ} \text{s}$ is equal to the mean value between the right-hand and left-hand limit values, i.e. actually zero.
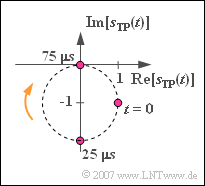
(4) The first and third suggested solutions are correct:
- With the carrier frequency $f_{\rm T} = f_{60} = 60 \ \text{ kHz}$ the equations for frequency and time domain are:
- $$S_{\rm TP}(f ) = S_{\rm +}(f+ f_{\rm 60}) = -{\rm j} \cdot \delta (f) + \delta (f + f_{\rm 10}) ;$$
- $$s_{\rm TP}(t) = - {\rm j} + 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }.$$
In the graph, $s_{\rm TP}(t)$ is shown. It can be seen:
- The locality curve is again a circle with radius $1$, but now with centre $(0, –{\rm j})$.
- Here, too: $s_{\rm TP}(t = 0) = 1 - {\rm j}$.
- You now move clockwise on the locality curve.
- The period continues to be $T_0 = 1/f_{10} = 100 \ µ \text{s}$.
- The locality curve is now rotated by $90^\circ$ in the complex plane compared to sub-task (1).
- For all times, the same pointer lengths result as for $f_{\rm T} = f_{50}$. The magnitude remains the same.
- The phase function $\phi(t)$ now yields values between $-\pi$ and zero, while the phase function calculated in subtask (3) has assumed values between $\pm \pi/2$.
- It is valid for all times $t$: $\phi_{\rm subtask \ (4)}= -(\phi_{\rm subtask \ (3)} + 90^\circ).$