Difference between revisions of "Aufgaben:Exercise 5.5Z: ACF after 1st Order Filter"
From LNTwww
m (Nabil verschob die Seite Zusatzaufgaben:5.5 AKF nach Filter 1. Ordnung nach 5.5Z AKF nach Filter 1. Ordnung) |
|||
| (23 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Creation_of_Predefined_ACF_Properties |
}} | }} | ||
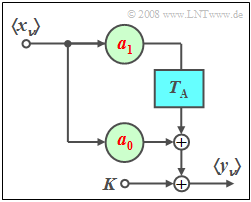
| − | [[File:P_ID565__Sto_Z_5_5_neu.png|right|]] | + | [[File:P_ID565__Sto_Z_5_5_neu.png|right|frame|Non-recursive filter <br>with DC component]] |
| − | + | We consider here a first order non-recursive filter $(M = 1)$. | |
| + | *Let the filter coefficients be $a_0 = 0.4$ and $a_1 = 0.3$. | ||
| + | *A constant $K$ is added at the filter output, which is to be set to zero up to and including subtask '''(3)'''. | ||
| − | |||
| − | |||
| − | |||
| − | + | The individual elements of the input sequence $\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle$ | |
| + | * are Gaussian as well as mean-free, and | ||
| + | * have in each case the standard deviation $\sigma_x = 1$. | ||
| − | === | + | |
| + | |||
| + | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Creation_of_Predefined_ACF_Properties|Creation of Predefined ACF Properties]]. | ||
| + | *Reference is also made to the chapters [[Theory_of_Stochastic_Signals/Auto-Correlation_Function_(ACF)|Auto-Correlation Function]] and [[Theory_of_Stochastic_Signals/Power-Spectral_Density|Power-Spectral Density]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are true regarding the output ACF when $K = 0$? Justify your results. |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The ACF value $\varphi_y(0)$ indicates the standard deviation $\sigma_y$. |
| − | + | + | + All ACF values $\varphi_y(k \cdot T_{\rm A})$ with $k \ge 2$ are zero. |
| − | + | + | + The power-spectral density $\rm (PSD)$ ${\it \Phi}_y(f)$ is cosinusoidal. |
| − | { | + | {Calculate the ACF values $\varphi_y(k \cdot T_{\rm A})$ for $k = 0$ and $k = 1$. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\varphi_y(0) \ = \ $ { 0.25 3% } |
| − | $\ | + | $\varphi_y(T_{\rm A}) \ = $ { 0.12 3% } |
| − | { | + | {What values do you need to set for $a_0$ and $a_1$ if you want the standard deviation to be $\sigma_y = 1$ for the same ACF shape? Let $a_0 > a_1$. |
|type="{}"} | |type="{}"} | ||
| − | $a_0$ | + | $a_0 \ = \ $ { 0.8 3% } |
| − | $a_1$ | + | $a_1 \ = \ $ { 0.6 3% } |
| − | { | + | {Let $a_0 = 0.4$ and $a_1 = 0.3$. How large should the constant $K$ be chosen so that $\varphi_y(0)= 0.5$? |
|type="{}"} | |type="{}"} | ||
| − | $K$ | + | $K \ = \ $ { 0.5 3% } |
| − | { | + | {Using this $K$ value, calculate the ACF values for $k = 1$ and $k = 2$. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\varphi_y(T_{\rm A}) \ = \ $ { 0.37 3% } |
| − | $\ | + | $\varphi_y(2 \cdot T_{\rm A}) \ = \ $ { 0.25 3% } |
| − | { | + | {What is the standard deviation $\sigma_y$ now? |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_y$ | + | $\sigma_y \ = \ $ { 0.5 3% } |
| Line 54: | Line 64: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' <u>Solutions 2 and 3</u> are correct: | |
| + | *The ACF value $\varphi_y(0)$ gives the variance ("power") $\sigma_y^2$ and not the "standard deviation" $\sigma_y$. | ||
| + | *Since a first-order non-recursive filter is present, all ACF values are $\varphi_y(k \cdot T_{\rm A})= 0$ for $|k| \ge 2$. | ||
| + | *The ACF value $\varphi_y(- T_{\rm A})$ is equal to $\varphi_y(+ T_{\rm A})$. | ||
| + | *These two ACF values result in a cosine function in the power-spectral density, to which the DC component $\varphi_y(0)$ is added. | ||
| + | |||
| + | |||
| − | + | '''(2)''' The general equation with $M = 1$ for $k \in \{0, \ 1\}$ is: | |
:$$\varphi _y ( {k \cdot T_{\rm A} } ) = \sigma _x ^2 \cdot \sum\limits_{\mu = 0}^{M - k} {a_\mu \cdot a_{\mu + k} } .$$ | :$$\varphi _y ( {k \cdot T_{\rm A} } ) = \sigma _x ^2 \cdot \sum\limits_{\mu = 0}^{M - k} {a_\mu \cdot a_{\mu + k} } .$$ | ||
| − | + | *From this we obtain with $\sigma_x = 1$: | |
:$$\varphi _y( 0 ) = a_0 ^2 + a_1 ^2 = 0.4^2 + 0.3^2 \hspace{0.15cm}\underline { = 0.25},$$ | :$$\varphi _y( 0 ) = a_0 ^2 + a_1 ^2 = 0.4^2 + 0.3^2 \hspace{0.15cm}\underline { = 0.25},$$ | ||
:$$\varphi _y ( { T_{\rm A} } ) = a_0 \cdot a_1 = 0.4 \cdot 0.3 \hspace{0.15cm}\underline {= 0.12}.$$ | :$$\varphi _y ( { T_{\rm A} } ) = a_0 \cdot a_1 = 0.4 \cdot 0.3 \hspace{0.15cm}\underline {= 0.12}.$$ | ||
| − | + | ||
| + | |||
| + | '''(3)''' With the previous settings, the variance is $\sigma_y^2 = 0.25$ and thus the standard deviation $\sigma_y = 0.5$. | ||
| + | *Doubling the coefficients gives $\sigma_y = 1$ as desired: | ||
:$$\hspace{0.15cm}\underline {a_0 = 0.8},\quad \hspace{0.15cm}\underline {a_1 = 0.6}.$$ | :$$\hspace{0.15cm}\underline {a_0 = 0.8},\quad \hspace{0.15cm}\underline {a_1 = 0.6}.$$ | ||
| − | + | ||
| + | |||
| + | '''(4)''' The constant $K$ raises the total ACF by $K^2$. Using the result from '''(2)''', it follows: | ||
:$$K^2 = 0.5 - 0.25 = 0.25\quad \Rightarrow \quad \hspace{0.15cm}\underline {K = 0.5}.$$ | :$$K^2 = 0.5 - 0.25 = 0.25\quad \Rightarrow \quad \hspace{0.15cm}\underline {K = 0.5}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | : | + | |
| + | '''(5)''' All ACF values are now larger by the constant value $K^2 = 0.25$. Thus | ||
| + | :$$\varphi _y ( { T_{\rm A} } ) = 0.12 + 0.25 \hspace{0.15cm}\underline {= 0.37},$$ | ||
| + | :$$\varphi _y ( { 2T_{\rm A} } ) = 0 + 0.25 \hspace{0.15cm}\underline {= 0.25}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' The constant $K$ does not change the standard deviation, i.e. $\sigma_y = 0.5$ is still valid. | ||
| + | *Formally, this quantity can also be calculated as follows: | ||
:$$\sigma _y ^2 = \varphi _y ( 0 ) - \mathop {\lim }\limits_{k \to \infty } \varphi _y ( {k \cdot T_{\rm A} } ) = 0.5 - 0.25 = 0.25.$$ | :$$\sigma _y ^2 = \varphi _y ( 0 ) - \mathop {\lim }\limits_{k \to \infty } \varphi _y ( {k \cdot T_{\rm A} } ) = 0.5 - 0.25 = 0.25.$$ | ||
| − | + | *Again, this gives $\sigma_y \hspace{0.15cm}\underline {= 0.5}$. | |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 84: | Line 109: | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^5.3 Filter Matching to ACF^]] |
Latest revision as of 12:07, 25 February 2022
We consider here a first order non-recursive filter $(M = 1)$.
- Let the filter coefficients be $a_0 = 0.4$ and $a_1 = 0.3$.
- A constant $K$ is added at the filter output, which is to be set to zero up to and including subtask (3).
The individual elements of the input sequence $\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle$
- are Gaussian as well as mean-free, and
- have in each case the standard deviation $\sigma_x = 1$.
Notes:
- The exercise belongs to the chapter Creation of Predefined ACF Properties.
- Reference is also made to the chapters Auto-Correlation Function and Power-Spectral Density.
Questions
Solution
(1) Solutions 2 and 3 are correct:
- The ACF value $\varphi_y(0)$ gives the variance ("power") $\sigma_y^2$ and not the "standard deviation" $\sigma_y$.
- Since a first-order non-recursive filter is present, all ACF values are $\varphi_y(k \cdot T_{\rm A})= 0$ for $|k| \ge 2$.
- The ACF value $\varphi_y(- T_{\rm A})$ is equal to $\varphi_y(+ T_{\rm A})$.
- These two ACF values result in a cosine function in the power-spectral density, to which the DC component $\varphi_y(0)$ is added.
(2) The general equation with $M = 1$ for $k \in \{0, \ 1\}$ is:
- $$\varphi _y ( {k \cdot T_{\rm A} } ) = \sigma _x ^2 \cdot \sum\limits_{\mu = 0}^{M - k} {a_\mu \cdot a_{\mu + k} } .$$
- From this we obtain with $\sigma_x = 1$:
- $$\varphi _y( 0 ) = a_0 ^2 + a_1 ^2 = 0.4^2 + 0.3^2 \hspace{0.15cm}\underline { = 0.25},$$
- $$\varphi _y ( { T_{\rm A} } ) = a_0 \cdot a_1 = 0.4 \cdot 0.3 \hspace{0.15cm}\underline {= 0.12}.$$
(3) With the previous settings, the variance is $\sigma_y^2 = 0.25$ and thus the standard deviation $\sigma_y = 0.5$.
- Doubling the coefficients gives $\sigma_y = 1$ as desired:
- $$\hspace{0.15cm}\underline {a_0 = 0.8},\quad \hspace{0.15cm}\underline {a_1 = 0.6}.$$
(4) The constant $K$ raises the total ACF by $K^2$. Using the result from (2), it follows:
- $$K^2 = 0.5 - 0.25 = 0.25\quad \Rightarrow \quad \hspace{0.15cm}\underline {K = 0.5}.$$
(5) All ACF values are now larger by the constant value $K^2 = 0.25$. Thus
- $$\varphi _y ( { T_{\rm A} } ) = 0.12 + 0.25 \hspace{0.15cm}\underline {= 0.37},$$
- $$\varphi _y ( { 2T_{\rm A} } ) = 0 + 0.25 \hspace{0.15cm}\underline {= 0.25}.$$
(6) The constant $K$ does not change the standard deviation, i.e. $\sigma_y = 0.5$ is still valid.
- Formally, this quantity can also be calculated as follows:
- $$\sigma _y ^2 = \varphi _y ( 0 ) - \mathop {\lim }\limits_{k \to \infty } \varphi _y ( {k \cdot T_{\rm A} } ) = 0.5 - 0.25 = 0.25.$$
- Again, this gives $\sigma_y \hspace{0.15cm}\underline {= 0.5}$.