Difference between revisions of "Aufgaben:Exercise 5.6Z: Filter Dimensioning again"
m (Text replacement - "Category:Aufgaben zu Stochastische Signaltheorie" to "Category:Theory of Stochastic Signals: Exercises") |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Creation_of_Predefined_ACF_Properties |
}} | }} | ||
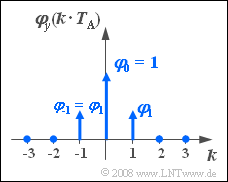
| − | [[File:P_ID567__Sto_Z_5_6.png|right|frame| | + | [[File:P_ID567__Sto_Z_5_6.png|right|frame|Desired ACF $\varphi_y(k \cdot T_{\rm A})$]] |
| − | + | Using a first-order non-recursive digital filter, generate a discrete-time random sequence $\left\langle \hspace{0.05cm} {y_\nu } \hspace{0.05cm} \right\rangle$ that has the following ACF values: | |
| − | :$$\varphi _y ( {k \cdot T_{\rm A} } ) = \left\{ {\begin{array}{*{20}c} {\varphi _0 = 1} & {\rm | + | :$$\varphi _y ( {k \cdot T_{\rm A} } ) = \left\{ {\begin{array}{*{20}c} {\varphi _0 = 1} & {\rm for} & {k = 0} \\ {\varphi _1 } & {\rm for} & {\left| k \right| = 1} \\ 0 & {} & {{\rm{otherwise}}.} \\ \end{array}} \right.$$ |
| − | + | Here $\varphi_1$ denotes a parameter that can be freely chosen (within certain limits). | |
| − | + | Further, it holds: | |
| − | * | + | * The discrete-time input values $x_\nu$ are Gaussian distributed with mean $m_x$ and standard deviation $\sigma_x$. |
| − | * | + | * For the whole exercise $\sigma_x= 1$ is valid. The mean value is initially $m_x = 0$. |
| − | *In | + | *In the subtask '''(4)''' $m_x = 1$ is valid. |
| − | + | Thus the system of equations for the determination of the filter coefficients $a_0$ and $a_1$ is: | |
| − | :$$a_0 ^2 + a_1 ^2 = 1, | + | :$$a_0 ^2 + a_1 ^2 = 1, $$ |
| − | a_0 \cdot a_1 = \varphi_1 .$$ | + | :$$a_0 \cdot a_1 = \varphi_1 .$$ |
| Line 26: | Line 26: | ||
| − | + | Notes: | |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Creation_of_Predefined_ACF_Properties|Creation of Predefined ACF Properties]]. |
| − | * | + | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Auto-Correlation_Function_(ACF)|Auto-Correlation Function]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the allowable limits for $\varphi_1$, so that the system of equations is solvable? |
|type="{}"} | |type="{}"} | ||
$\varphi_\text{1, max} \ = \ $ { 0.5 3% } | $\varphi_\text{1, max} \ = \ $ { 0.5 3% } | ||
| Line 42: | Line 42: | ||
| − | { | + | {Let $\varphi_1= -0.3$. Determine the filter parameters $a_0$ and $a_1$. Choose the solution with positive $a_0$ and $|a_1| < a_0$. |
|type="{}"} | |type="{}"} | ||
$a_0 \ = \ $ { 0.949 3% } | $a_0 \ = \ $ { 0.949 3% } | ||
| Line 48: | Line 48: | ||
| − | { | + | {How does the ACF change if now $\sigma_x = 2$ with the same filter coefficients? In particular, what is the value of the ACF for $k = 1 $? |
|type="{}"} | |type="{}"} | ||
$\varphi_y(T_{\rm A}) \ = \ $ { -1.236--1.164 } | $\varphi_y(T_{\rm A}) \ = \ $ { -1.236--1.164 } | ||
| − | { | + | {How does the ACF change with the same filter coefficients and $\sigma_x = 2$ with a DC component $m_x = 1$? Now what is the ACF value for $k = 1 $? |
|type="{}"} | |type="{}"} | ||
$\varphi_y(T_{\rm A}) \ = \ $ { -0.82--0.78 } | $\varphi_y(T_{\rm A}) \ = \ $ { -0.82--0.78 } | ||
| Line 61: | Line 61: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' After some transformations we arrive at the equation of determination $($with $u = a_0^2)$: |
:$$a_0 \cdot a_1 = \varphi_1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | :$$a_0 \cdot a_1 = \varphi_1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
a_1 = \varphi_1 /a_0 ,$$ | a_1 = \varphi_1 /a_0 ,$$ | ||
| Line 72: | Line 72: | ||
u^2 - u + \varphi_1^2 = 0.$$ | u^2 - u + \varphi_1^2 = 0.$$ | ||
| − | * | + | *This leads to the two solutions: |
:$$u_{1/2} = 0.5 \pm \sqrt {0.25 - \varphi _1 ^2 } .$$ | :$$u_{1/2} = 0.5 \pm \sqrt {0.25 - \varphi _1 ^2 } .$$ | ||
| − | * | + | *Real solutions exist only for $\varphi_1^2 \le 0.25$, which means: |
:$$\hspace{0.15cm}\underline {\varphi_\text{1, max} = +0.5}, \quad \hspace{0.15cm}\underline {\varphi_\text{1, min} = - 0.5}.$$ | :$$\hspace{0.15cm}\underline {\varphi_\text{1, max} = +0.5}, \quad \hspace{0.15cm}\underline {\varphi_\text{1, min} = - 0.5}.$$ | ||
| − | '''(2)''' | + | '''(2)''' With $\varphi_1=-0.3$, we get $u_1 = 0.9$ and $u_2 = 0.1$ resulting in the following sets of parameters: |
| − | :$$\text{ | + | :$$\text{Solution 1:} \ \ a_0 = \;\;\,\sqrt {0.9} = \;\;\, 0.949,\quad a_1 = - \sqrt {0.1} = - 0.316;$$ |
| − | :$$\text{ | + | :$$\text{Solution 2:} \ \ a_0 = - \sqrt {0.9} = - 0.949,\quad a_1 = \;\;\, \sqrt {0.1} = \;\;\, 0.316;$$ |
| − | :$$\text{ | + | :$$\text{Solution 3:} \ \ a_0 = \;\;\, \sqrt {0.1} = \;\;\, 0.316,\quad a_1 = - \sqrt {0.9} = - 0.949;$$ |
| − | :$$\text{ | + | :$$\text{Solution 4:} \ \ a_0 = - \sqrt {0.1} = - 0.316,\quad a_1 = \;\;\, \sqrt {0.9} = \;\;\, 0.949.$$ |
| − | * | + | *Only the first parameter set satisfies the specified constraint: |
:$$a_0 \hspace{0.15cm}\underline {= 0.949} \ \text{ und } \ a_1 \hspace{0.15cm}\underline {= -0.316}.$$ | :$$a_0 \hspace{0.15cm}\underline {= 0.949} \ \text{ und } \ a_1 \hspace{0.15cm}\underline {= -0.316}.$$ | ||
| − | '''(3)''' | + | '''(3)''' If $\sigma_x$ is doubled, all ACF values increase by a factor of $4$. In particular, then holds: |
:$$\varphi _y( {T_{\rm A} } ) = - 0.3 \cdot 4 \hspace{0.15cm}\underline{= - 1.2}.$$ | :$$\varphi _y( {T_{\rm A} } ) = - 0.3 \cdot 4 \hspace{0.15cm}\underline{= - 1.2}.$$ | ||
| − | '''(4)''' | + | '''(4)''' The DC component $m_x = 1$ at the input leads to the following DC component in the output signal: |
:$$m_y = m_x \cdot ( {a_0 + a_1 } ) = 1 \cdot (0.949 -0.316) = 0.633.$$ | :$$m_y = m_x \cdot ( {a_0 + a_1 } ) = 1 \cdot (0.949 -0.316) = 0.633.$$ | ||
| − | * | + | *All ACF values are therefore increased by $m_y^2 \approx 0.4$ compared to subtask '''(3)''' and we now obtain: |
:$$\varphi _y( {T_{\rm A} } )\hspace{0.15cm}\underline{ \approx - 0.8}.$$ | :$$\varphi _y( {T_{\rm A} } )\hspace{0.15cm}\underline{ \approx - 0.8}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 104: | Line 104: | ||
| − | [[Category:Theory of Stochastic Signals: Exercises|^5.3 | + | [[Category:Theory of Stochastic Signals: Exercises|^5.3 Filter Matching to ACF^]] |
Latest revision as of 12:34, 21 February 2022
Using a first-order non-recursive digital filter, generate a discrete-time random sequence $\left\langle \hspace{0.05cm} {y_\nu } \hspace{0.05cm} \right\rangle$ that has the following ACF values:
- $$\varphi _y ( {k \cdot T_{\rm A} } ) = \left\{ {\begin{array}{*{20}c} {\varphi _0 = 1} & {\rm for} & {k = 0} \\ {\varphi _1 } & {\rm for} & {\left| k \right| = 1} \\ 0 & {} & {{\rm{otherwise}}.} \\ \end{array}} \right.$$
Here $\varphi_1$ denotes a parameter that can be freely chosen (within certain limits).
Further, it holds:
- The discrete-time input values $x_\nu$ are Gaussian distributed with mean $m_x$ and standard deviation $\sigma_x$.
- For the whole exercise $\sigma_x= 1$ is valid. The mean value is initially $m_x = 0$.
- In the subtask (4) $m_x = 1$ is valid.
Thus the system of equations for the determination of the filter coefficients $a_0$ and $a_1$ is:
- $$a_0 ^2 + a_1 ^2 = 1, $$
- $$a_0 \cdot a_1 = \varphi_1 .$$
Notes:
- The exercise belongs to the chapter Creation of Predefined ACF Properties.
- Reference is also made to the chapter Auto-Correlation Function.
Questions
Solution
- $$a_0 \cdot a_1 = \varphi_1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} a_1 = \varphi_1 /a_0 ,$$
- $$a_0^2 + a_1^2 = 1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} a_0^2 + \varphi_1^2 /a_0^2 -1 = 0,$$
- $$u = a_0^2 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} u + \varphi_1^2 /u -1 = 0 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} u^2 - u + \varphi_1^2 = 0.$$
- This leads to the two solutions:
- $$u_{1/2} = 0.5 \pm \sqrt {0.25 - \varphi _1 ^2 } .$$
- Real solutions exist only for $\varphi_1^2 \le 0.25$, which means:
- $$\hspace{0.15cm}\underline {\varphi_\text{1, max} = +0.5}, \quad \hspace{0.15cm}\underline {\varphi_\text{1, min} = - 0.5}.$$
(2) With $\varphi_1=-0.3$, we get $u_1 = 0.9$ and $u_2 = 0.1$ resulting in the following sets of parameters:
- $$\text{Solution 1:} \ \ a_0 = \;\;\,\sqrt {0.9} = \;\;\, 0.949,\quad a_1 = - \sqrt {0.1} = - 0.316;$$
- $$\text{Solution 2:} \ \ a_0 = - \sqrt {0.9} = - 0.949,\quad a_1 = \;\;\, \sqrt {0.1} = \;\;\, 0.316;$$
- $$\text{Solution 3:} \ \ a_0 = \;\;\, \sqrt {0.1} = \;\;\, 0.316,\quad a_1 = - \sqrt {0.9} = - 0.949;$$
- $$\text{Solution 4:} \ \ a_0 = - \sqrt {0.1} = - 0.316,\quad a_1 = \;\;\, \sqrt {0.9} = \;\;\, 0.949.$$
- Only the first parameter set satisfies the specified constraint:
- $$a_0 \hspace{0.15cm}\underline {= 0.949} \ \text{ und } \ a_1 \hspace{0.15cm}\underline {= -0.316}.$$
(3) If $\sigma_x$ is doubled, all ACF values increase by a factor of $4$. In particular, then holds:
- $$\varphi _y( {T_{\rm A} } ) = - 0.3 \cdot 4 \hspace{0.15cm}\underline{= - 1.2}.$$
(4) The DC component $m_x = 1$ at the input leads to the following DC component in the output signal:
- $$m_y = m_x \cdot ( {a_0 + a_1 } ) = 1 \cdot (0.949 -0.316) = 0.633.$$
- All ACF values are therefore increased by $m_y^2 \approx 0.4$ compared to subtask (3) and we now obtain:
- $$\varphi _y( {T_{\rm A} } )\hspace{0.15cm}\underline{ \approx - 0.8}.$$