Difference between revisions of "Digital Signal Transmission/Basics of Coded Transmission"
| Line 146: | Line 146: | ||
| − | * | + | *Also the signal $s_{\rm R}(t)$ with NRZ rectangular pulses is non–stationary in a strict sense, because here the moments at the bit boundaries differ with respect to all other instants. For example, $s_{\rm R}(t = \pm T/2)=0$. |
<br clear=all> | <br clear=all> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ A random process whose moments $m_k(t) = m_k(t+ \nu \cdot T)$ repeat periodically with $T$ is called '''cyclostationary'''; $k$ and $\nu$ have integer values in this implicit definition.}} |
| − | + | Many of the rules valid for [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Ergodic_random_processes|ergodic processes]] can also be applied to ''cycloergodic'' (and hence to ''cyclostationary'' ) processes with only minor restrictions. | |
| − | + | In particular, for the [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Random_processes|auto-correlation function]] (ACF) of such random processes with sample signal $s(t)$ holds: | |
:$$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] \hspace{0.05cm}.$$ | :$$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] \hspace{0.05cm}.$$ | ||
| − | + | With the above equation of the transmitted signal, the ACF as a time average can also be written as follows: | |
:$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}\frac{1}{T} | :$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}\frac{1}{T} | ||
\cdot \lim_{N \to \infty} \frac{1}{2N +1} \cdot \sum_{\nu = | \cdot \lim_{N \to \infty} \frac{1}{2N +1} \cdot \sum_{\nu = | ||
| Line 163: | Line 163: | ||
\lambda \cdot T)\,{\rm d} t \hspace{0.05cm}.$$ | \lambda \cdot T)\,{\rm d} t \hspace{0.05cm}.$$ | ||
| − | + | Since the limit, integral and sum may be interchanged, with the substitutions $N = T_{\rm M}/(2T)$, $\lambda = \kappa- \nu$ and $t - \nu \cdot T \to T$ for this can also be written: | |
:$$\varphi_s(\tau) = \lim_{T_{\rm M} \to \infty}\frac{1}{T_{\rm M}} | :$$\varphi_s(\tau) = \lim_{T_{\rm M} \to \infty}\frac{1}{T_{\rm M}} | ||
\cdot | \cdot | ||
| Line 171: | Line 171: | ||
a_\kappa \cdot g_s ( t + \tau - \kappa \cdot T ) | a_\kappa \cdot g_s ( t + \tau - \kappa \cdot T ) | ||
\,{\rm d} t \hspace{0.05cm}.$$ | \,{\rm d} t \hspace{0.05cm}.$$ | ||
| − | + | Now the following quantities are introduced for abbreviation: | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ The '''discrete ACF of the amplitude coefficients''' provides statements about the linear statistical bonds of the amplitude coefficients $a_{\nu}$ and $a_{\nu + \lambda}$ and has no unit: |
:$$\varphi_a(\lambda) = \lim_{N \to \infty} \frac{1}{2N +1} \cdot | :$$\varphi_a(\lambda) = \lim_{N \to \infty} \frac{1}{2N +1} \cdot | ||
\sum_{\nu = -\infty}^{+\infty} a_\nu \cdot a_{\nu + \lambda} | \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot a_{\nu + \lambda} | ||
| Line 181: | Line 181: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ The '''energy ACF''' of the basic pulse is defined similarly to the general (power) ACF. It is marked with a dot. Since $g_s(t)$ is [[Signal_Representation/Signal_classification#Energy.E2.80.93Limited_and_Power.E2.80.93Limited_Signals| energy-limited]], the division by $T_{\rm M}$ and the boundary transition can be omitted: |
:$$\varphi^{^{\bullet} }_{gs}(\tau) = | :$$\varphi^{^{\bullet} }_{gs}(\tau) = | ||
\int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + | \int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + | ||
| Line 188: | Line 188: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ For the '''auto-correlation function of a digital signal''' $s(t)$ holds in general: |
:$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} | :$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} | ||
\cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - | \cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - | ||
\lambda \cdot T)\hspace{0.05cm}.$$ | \lambda \cdot T)\hspace{0.05cm}.$$ | ||
| − | + | The signal $s(t)$ can be binary or multi-level, unipolar or bipolar as well as redundancy-free or redundant (line-coded). The pulse shape is taken into account by the energy ACF.}} | |
| − | + | If the digital signal $s(t)$ describes a voltage waveform, the energy ACF of the basic pulse $g_s(t)$ has the unit $\rm V^2s$ and $\varphi_s(\tau)$ has the unit $\rm V^2$, each related to the resistor $1 \ \rm \Omega$. | |
| − | <i> | + | <i>Note:</i> In the strict sense of system theory, one would have to define the ACF of the amplitude coefficients as follows: |
:$$\varphi_{a , \hspace{0.08cm}\delta}(\tau) = \sum_{\lambda = -\infty}^{+\infty} | :$$\varphi_{a , \hspace{0.08cm}\delta}(\tau) = \sum_{\lambda = -\infty}^{+\infty} | ||
\varphi_a(\lambda)\cdot \delta(\tau - \lambda \cdot | \varphi_a(\lambda)\cdot \delta(\tau - \lambda \cdot | ||
T)\hspace{0.05cm}.$$ | T)\hspace{0.05cm}.$$ | ||
| − | + | Thus, the above equation would be as follows: | |
:$$\varphi_s(\tau) ={1}/{T} \cdot \varphi_{a , \hspace{0.08cm} | :$$\varphi_s(\tau) ={1}/{T} \cdot \varphi_{a , \hspace{0.08cm} | ||
\delta}(\tau)\star \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot | \delta}(\tau)\star \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot | ||
| Line 208: | Line 208: | ||
\varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda | \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda | ||
\cdot T)\hspace{0.05cm}.$$ | \cdot T)\hspace{0.05cm}.$$ | ||
| − | + | For simplicity, the discrete ACF of amplitude coefficients | |
⇒ $\varphi_a(\lambda)$ | ⇒ $\varphi_a(\lambda)$ | ||
| − | + | is written without these Dirac delta functions in the following.<br> | |
| − | == | + | == PSD calculation of a digital signal == |
<br> | <br> | ||
| − | + | The corresponding quantity to the auto-correlation function (ACF) of a random signal ⇒ $\varphi_s(\tau)$ in the frequency domain is the [[Theory_of_Stochastic_Signals/Power-Spectral_Density#Wiener-Khintchine_Theorem|power-spectral density]] (PSD) ⇒ ${\it \Phi}_s(f)$, which is in a fixed relation with the ACF via the Fourier integral:<br> | |
:$$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} | :$$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} | ||
{\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot | {\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot | ||
{\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \tau} | {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \tau} | ||
\,{\rm d} \tau \hspace{0.05cm}.$$ | \,{\rm d} \tau \hspace{0.05cm}.$$ | ||
| − | + | Considering the relation between energy ACF and energy spectrum, | |
:$$\varphi^{^{\hspace{0.05cm}\bullet}}_{gs}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} | :$$\varphi^{^{\hspace{0.05cm}\bullet}}_{gs}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} | ||
{\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{gs}(f) = |G_s(f)|^2 | {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{gs}(f) = |G_s(f)|^2 | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | + | and the [[Signal_Representation/Fourier_Transform_Theorems#Shifting_Theorem|shifting theorem]], the power-spectral density of the digital signal $s(t)$ can be represented in the following way: | |
:$${\it \Phi}_s(f) = \sum_{\lambda = | :$${\it \Phi}_s(f) = \sum_{\lambda = | ||
-\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot {\it | -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot {\it | ||
| Line 231: | Line 231: | ||
-\infty}^{+\infty}\varphi_a(\lambda)\cdot \cos ( | -\infty}^{+\infty}\varphi_a(\lambda)\cdot \cos ( | ||
2 \pi f \lambda T)\hspace{0.05cm}.$$ | 2 \pi f \lambda T)\hspace{0.05cm}.$$ | ||
| − | + | Here it is considered that ${\it \Phi}_s(f)$ and $|G_s(f)|^2$ are real-valued and at the same time $\varphi_a(-\lambda) =\varphi_a(+\lambda)$ holds.<br><br> | |
| − | + | If we now define the '''spectral power density of the amplitude coefficients''' to be | |
:$${\it \Phi}_a(f) = \sum_{\lambda = | :$${\it \Phi}_a(f) = \sum_{\lambda = | ||
-\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm | -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm | ||
| Line 239: | Line 239: | ||
1}^{\infty}\varphi_a(\lambda)\cdot\cos ( 2 \pi f | 1}^{\infty}\varphi_a(\lambda)\cdot\cos ( 2 \pi f | ||
\lambda T) \hspace{0.05cm},$$ | \lambda T) \hspace{0.05cm},$$ | ||
| − | + | then the following expression is obtained: | |
:$${\it \Phi}_s(f) = {\it \Phi}_a(f) \cdot {1}/{T} \cdot | :$${\it \Phi}_s(f) = {\it \Phi}_a(f) \cdot {1}/{T} \cdot | ||
|G_s(f)|^2 \hspace{0.05cm}.$$ | |G_s(f)|^2 \hspace{0.05cm}.$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ The power-spectral density ${\it \Phi}_s(f)$ of a digital signal $s(t)$ can be represented as the product of two functions: |
| − | * | + | *The first term ${\it \Phi}_a(f)$ is dimensionless and describes the spectral shaping of the transmitted signal by ''the statistical constraints of the source''.<br> |
| − | * | + | *In contrast, $\vert G_s(f) \vert^2$ takes into account the ''spectral shaping by the basic transmission pulse'' $g_s(t)$. The narrower this is, the broader is $\vert G_s(f) \vert^2$ and thus the larger is the bandwidth requirement.<br> |
| − | * | + | *The energy spectrum has the unit $\rm V^2s/Hz$ and the power-spectral density – due to the division by the symbol distance $T$ – the unit $\rm V^2/Hz$. Both specifications are again only valid for the resistor $1 \ \rm \Omega$.}} |
| − | == | + | == ACF and PSD for bipolar binary signals == |
<br> | <br> | ||
| − | + | The previous results are now illustrated by examples. Starting from <i>binary bipolar amplitude coefficients</i> $a_\nu \in \{-1, +1\}$, if there are no bonds between the individual amplitude coefficients $a_\nu$, we obtain:<br> | |
:$$\varphi_a(\lambda) = \left\{ \begin{array}{c} 1 | :$$\varphi_a(\lambda) = \left\{ \begin{array}{c} 1 | ||
\\ 0 \\ \end{array} \right.\quad | \\ 0 \\ \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm{ | + | \begin{array}{*{1}c} {\rm{for}}\\ {\rm{for}} \\ \end{array} |
\begin{array}{*{20}c}\lambda = 0, \\ \lambda \ne 0 \\ | \begin{array}{*{20}c}\lambda = 0, \\ \lambda \ne 0 \\ | ||
\end{array} | \end{array} | ||
| Line 261: | Line 261: | ||
{1}/{T} \cdot \varphi^{^{\bullet}}_{gs}(\tau)\hspace{0.05cm}.$$ | {1}/{T} \cdot \varphi^{^{\bullet}}_{gs}(\tau)\hspace{0.05cm}.$$ | ||
| − | + | The graph shows two signal sections each with rectangular pulses $g_s(t)$, which accordingly lead to a triangular ACF and to a $\rm si^2$–shaped power-spectral density (PSD). | |
| − | [[File:P_ID1306__Dig_T_2_1_S6_v2.png|right|frame| | + | [[File:P_ID1306__Dig_T_2_1_S6_v2.png|right|frame|Signal section, ACF and PSD for binary bipolar signaling|class=fit]] |
| − | * | + | *The left pictures describe a NRZ signaling. That means: The width $T_{\rm S}$ of the basic pulse is equal to the distance $T$ of two transmitted pulses (source symbols). |
| − | * | + | *In contrast, the right pictures apply to an RZ pulse with the duty cycle $T_{\rm S}/T = 0.5$. |
| − | + | One can see from these representations: | |
| − | * | + | *For NRZ rectangular pulses, the transmit power (referenced to the $1 \ \rm \Omega$ resistor) is $P_{\rm S} = \varphi_s(\tau = 0) = s_0^2$ and the triangular ACF is limited to the range $|\tau| \le T_{\rm S}= T$. <br> |
| − | * | + | *The PSD ${\it \Phi}_s(f)$ as the Fourier transform of $\varphi_s(\tau)$ is $\rm si^2$–shaped with equidistant zeros at distance $1/T$. The area under the PSD curve again gives the transmit power $P_{\rm S} = s_0^2$.<br> |
| − | * | + | *In the case of RZ signaling (right column), the triangular ACF is smaller in height and width by a factor of $T_{\rm S}/T = 0.5$, respectively, compared to the left image.<br> |
<br clear=all> | <br clear=all> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ If one compares the two power-spectral densities (lower pictures), one recognizes for $T_{\rm S}/T = 0.5$ (RZ pulse) compared to $T_{\rm S}/T = 1$ (NRZ pulse) a reduction in height by a factor of $4$ and a broadening by a factor of $2$. The area (power) is thus half as large, since in half the time $s(t) = 0$. }} |
| − | == | + | == ACF and PSD for unipolar binary signals == |
<br> | <br> | ||
| − | + | We continue to assume NRZ or RZ rectangular pulses. But let the binary amplitude coefficients now be unipolar: $a_\nu \in \{0, 1\}$. <br>Then for the discrete ACF of the amplitude coefficients holds: | |
:$$\varphi_a(\lambda) = \left\{ \begin{array}{c} m_2 = 0.5 \\ | :$$\varphi_a(\lambda) = \left\{ \begin{array}{c} m_2 = 0.5 \\ | ||
\\ m_1^2 = 0.25 \\ \end{array} \right.\quad | \\ m_1^2 = 0.25 \\ \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm{ | + | \begin{array}{*{1}c} {\rm{for}}\\ \\ {\rm{for}} \\ \end{array} |
\begin{array}{*{20}c}\lambda = 0, \\ \\ \lambda \ne 0 \hspace{0.05cm}.\\ | \begin{array}{*{20}c}\lambda = 0, \\ \\ \lambda \ne 0 \hspace{0.05cm}.\\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | + | Assumed here are equal probability amplitude coefficients ⇒ ${\rm Pr}(a_\nu =0) = {\rm Pr}(a_\nu =1) = 0.5$ with no statistical ties, so that both the [[Theory_of_Stochastic_Signals/Moments_of_a_Discrete_Random_Variable#Second_order_moment_.E2.80.93_power_.E2.80.93_variance_.E2.80.93_standard_deviation|quadratic mean]] $m_2$ (power) and the [[Theory_of_Stochastic_Signals/Moments_of_a_Discrete_Random_Variable#First_order_moment_.E2.80.93_linear_mean_.E2.80.93_DC_component|linear mean]] $m_1$ (DC component) are $0.5$, respectively.<br> | |
| − | + | The graph shows a signal section, the ACF and the PSD with unipolar amplitude coefficients, | |
| − | [[File:EN_Dig_T_2_1_S7.png|right|frame| | + | [[File:EN_Dig_T_2_1_S7.png|right|frame|Signal section, ACF and PSD with binary unipolar signaling|class=fit]] |
| − | * | + | *left for rectangular NRZ pulses $(T_{\rm S}/T = 1)$ , and<br> |
| − | * | + | *right for RZ pulses with duty cycle $T_{\rm S}/T = 0.5$. |
| − | + | There are the following differences compared to [[Digital_Signal_Transmission/Grundlagen_der_codierten_Übertragung#AKF_und_LDS_bei_bipolaren_Bin.C3.A4rsignalen|bipolar signaling]]: | |
| − | *Durch die Addition der unendlich vielen Dreieckfunktionen im Abstand $T$, alle mit gleicher Höhe, ergibt sich für die | + | *Durch die Addition der unendlich vielen Dreieckfunktionen im Abstand $T$, alle mit gleicher Höhe, ergibt sich für die ACF in der linken Grafik (NRZ) ein konstanter Gleichanteil $s_0^2/4$. |
| − | *Daneben verbleibt im Bereich $|\tau| \le T_{\rm S}$ ein einzelnes Dreieck ebenfalls mit Höhe $s_0^2/4$, das im Leistungsdichtespektrum ( | + | *Daneben verbleibt im Bereich $|\tau| \le T_{\rm S}$ ein einzelnes Dreieck ebenfalls mit Höhe $s_0^2/4$, das im Leistungsdichtespektrum (PSD) zum $\rm si^2$–förmigen Verlauf führt (blaue Kurve).<br> |
| − | *Der Gleichanteil in der | + | *Der Gleichanteil in der ACF hat im PSD eine Diracfunktion bei der Frequenz $f = 0$ mit dem Gewicht $s_0^2/4$ zur Folge. Dadurch wird der PSD–Wert ${\it \Phi}_s(f=0)$ unendlich groß.<br> |
| − | Aus der rechten Grafik – gültig für $T_{\rm S}/T = 0.5$ – erkennt man, dass sich nun die | + | Aus der rechten Grafik – gültig für $T_{\rm S}/T = 0.5$ – erkennt man, dass sich nun die ACF aus einem periodischen Dreiecksverlauf (im mittleren Bereich gestrichelt eingezeichnet) und zusätzlich noch aus einem einmaligen Dreieck im Bereich $|\tau| \le T_{\rm S} = T/2$ mit Höhe $s_0^2/8$ zusammensetzt. |
*Diese einmalige Dreieckfunktion führt zum kontinuierlichen, $\rm si^2$–förmigen Anteil (blaue Kurve) von ${\it \Phi}_s(f)$ mit der ersten Nullstelle bei $1/T_{\rm S} = 2/T$. | *Diese einmalige Dreieckfunktion führt zum kontinuierlichen, $\rm si^2$–förmigen Anteil (blaue Kurve) von ${\it \Phi}_s(f)$ mit der ersten Nullstelle bei $1/T_{\rm S} = 2/T$. | ||
| Line 313: | Line 313: | ||
*Dagegen führt die periodische Dreieckfunktion nach den Gesetzmäßigkeiten der [[Signal_Representation/Fourier_Series#Allgemeine_Beschreibung| Fourierreihe]] zu einer unendlichen Summe von Diracfunktionen mit unterschiedlichen Gewichten im Abstand $1/T$ (rot gezeichnet).<br> | *Dagegen führt die periodische Dreieckfunktion nach den Gesetzmäßigkeiten der [[Signal_Representation/Fourier_Series#Allgemeine_Beschreibung| Fourierreihe]] zu einer unendlichen Summe von Diracfunktionen mit unterschiedlichen Gewichten im Abstand $1/T$ (rot gezeichnet).<br> | ||
| − | *Die Gewichte der Diracfunktionen sind proportional zum kontinuierlichen (blauen) | + | *Die Gewichte der Diracfunktionen sind proportional zum kontinuierlichen (blauen) PSD–Anteil. Das maximale Gewicht $s_0^2/8$ besitzt die Diraclinie bei $f = 0$. Dagegen sind die Diraclinien bei $\pm 2/T$ und Vielfachen davon nicht vorhanden bzw. besitzen jeweils das Gewicht $0$, da hier auch der kontinuierliche PSD–Anteil Nullstellen besitzt.<br> |
Revision as of 16:01, 7 April 2022
Contents
- 1 # OVERVIEW OF THE SECOND MAIN CHAPTER #
- 2 Information content – Entropy – Redundancy
- 3 Source coding – Channel coding – Transmission coding
- 4 System model and description variables
- 5 ACF calculation of a digital signal
- 6 PSD calculation of a digital signal
- 7 ACF and PSD for bipolar binary signals
- 8 ACF and PSD for unipolar binary signals
- 9 Aufgaben zum Kapitel
# OVERVIEW OF THE SECOND MAIN CHAPTER #
The second main chapter deals with so-called transmission coding, which is sometimes also referred to as "line coding" in the literature. In this process, an adaptation of the digital transmission signal to the characteristics of the transmission channel is achieved through the targeted addition of redundancy. In detail, the following are dealt with:
- some basic concepts of information theory such as information content and entropy,
- the ACF calculation and the power-spectral densities of digital signals,
- the redundancy-free coding, which leads to a non-binary transmitted signal,
- the calculation of symbol and bit error probability for multilevel systems,
- the so-called 4B3T codes as an important example of blockwise coding, and
- the pseudo-ternary codes, each of which realizes symbol-wise coding.
The description is in baseband throughout and some simplifying assumptions (among others: no intersymbol interfering) are still made.
Further information on the topic as well as exercises, simulations and programming exercises can be found in
- chapter 15: Coded and multilevel transmission, program cod
of the practical course "Simulation Methods in Communications Engineering". This (former) LNT course at the TU Munich is based on
- the teaching software package LNTsim ⇒ link refers to the ZIP version of the program and
- this lab manual ⇒ link refers to the PDF version; chapter 15: pages 337-362.
Information content – Entropy – Redundancy
We assume an $M$–stage digital message source that outputs the following source signal:
- $$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T)\hspace{0.3cm}{\rm with}\hspace{0.3cm}a_\nu \in \{ a_1, \text{...} \ , a_\mu , \text{...} \ , a_{ M}\}.$$
- The source symbol sequence $\langle q_\nu \rangle$ is thus mapped to the sequence $\langle a_\nu \rangle$ of the dimensionless amplitude coefficients.
- Simplifying, first for the time indexing variable $\nu = 1$, ... , $N$ is set, while the index $\mu$ can always assume values between $1$ and $M$.
If the $\nu$–th sequence element is equal to $a_\mu$, its information content can be calculated with probability $p_{\nu\mu} = {\rm Pr}(a_\nu = a_\mu)$ as follows:
- $$I_\nu = \log_2 \ (1/p_{\nu \mu})= {\rm ld} \ (1/p_{\nu \mu}) \hspace{1cm}\text{(unit: bit)}\hspace{0.05cm}.$$
The logarithm to the base 2 ⇒ $\log_2(x)$ is often also called ${\rm ld}(x)$ ⇒ logarithm dualis. With the numerical evaluation the reference unit "bit" (from: binary digit ) is added. With the tens logarithm $\lg(x)$ and the natural logarithm $\ln(x)$ applies:
- $${\rm log_2}(x) = \frac{{\rm lg}(x)}{{\rm lg}(2)}= \frac{{\rm ln}(x)}{{\rm ln}(2)}\hspace{0.05cm}.$$
According to this definition of information, which goes back to Claude E. Shannon, the smaller the probability of occurrence of a symbol, the greater its information content.
$\text{Definition:}$ Entropy is the average information content of a sequence element (symbol). This important information-theoretical quantity can be determined as a time average as follows:
- $$H = \lim_{N \to \infty} \frac{1}{N} \cdot \sum_{\nu = 1}^N I_\nu = \lim_{N \to \infty} \frac{1}{N} \cdot \sum_{\nu = 1}^N \hspace{0.1cm}{\rm log_2}\hspace{0.05cm} \ (1/p_{\nu \mu}) \hspace{1cm}\text{(unit: bit)}\hspace{0.05cm}.$$
Of course, entropy can also be calculated by ensemble averaging (over the symbol set).
If the sequence elements $a_\nu$ are statistically independent of each other, the probabilities of occurrence $p_{\nu\mu} = p_{\mu}$ are independent of $\nu$ and we obtain in this special case for the entropy:
- $$H = \sum_{\mu = 1}^M p_{ \mu} \cdot {\rm log_2}\hspace{0.1cm} \ (1/p_{\mu})\hspace{0.05cm}.$$
If, on the other hand, there are statistical bonds between neighboring amplitude coefficients $a_\nu$, the more complicated equation according to the above definition must be used for entropy calculation.
The maximum value of entropy is obtained whenever the $M$ occurrence probabilities (of the statistically independent symbols) are all equal $(p_{\mu} = 1/M)$:
- $$H_{\rm max} = \sum_{\mu = 1}^M \hspace{0.1cm}\frac{1}{M} \cdot {\rm log_2} (M) = {\rm log_2} (M) \cdot \sum_{\mu = 1}^M \hspace{0.1cm} \frac{1}{M} = {\rm log_2} (M) \hspace{1cm}\text{(unit: bit)}\hspace{0.05cm}.$$
$\text{Definition:}$ Let $H_{\rm max}$ be the decision content (or message content ) of the source and the quotient
- $$r = \frac{H_{\rm max}-H}{H_{\rm max} }$$
as the relative redundancy. Since $0 \le H \le H_{\rm max}$ always holds, the relative redundancy can take values between $0$ and $1$ (including these limits).
From the derivation of these descriptive quantities, it is obvious that a redundancy-free digital signal $(r=0)$ must satisfy the following properties:
- The amplitude coefficients $a_\nu$ are statistically independent ⇒ $p_{\nu\mu} = {\rm Pr}(a_\nu = a_\mu)$ is identical for all $\nu$.
- The $M$ possible coefficients $a_\mu$ occur with equal probability $p_\mu = 1/M$.
$\text{Example 1:}$ If one analyzes a German text waiting for transmission on the basis of $M = 32$ characters
- $$\text{(a, ... , z, ä, ö, ü, ß, spaces, punctuation, no distinction between upper and lower case)},$$
the result is the decision content $H_{\rm max} = 5 \ \rm bit/symbol$. Due to
- the different frequencies (for example, "e" occurs significantly more often than "u") and
- of statistical bindings (for example "q" is followed by the letter "u" much more often than "e")
according to Karl Küpfmüller the entropy of the German language is only $H = 1.3 \ \rm bit/character$. This results in a relative redundancy of $r \approx (5 - 1.3)/5 = 74\%$.
For English texts Claude Shannon has given the entropy as $H = 1 \ \rm bit/character$ and the relative redundancy as $r \approx 80\%$.
Source coding – Channel coding – Transmission coding
Coding is the conversion of the source symbol sequence $\langle q_\nu \rangle$ with symbol range $M_q$ into a code symbol sequence $\langle c_\nu \rangle$ with symbol range $M_c$. Usually, coding manipulates the redundancy contained in a digital signal. Often – but not always – $M_q$ and $M_c$ are different.
A distinction is made between different types of coding depending on the target direction:
- The task of source coding is redundancy reduction for data compression, as applied for example in image coding. By exploiting statistical bonds between the individual points of an image or between the brightness values of a point at different times (in the case of moving image sequences), methods can be developed that lead to a noticeable reduction in the amount of data (measured in "bit" or "byte") while maintaining virtually the same (subjective) image quality. A simple example of this is differential pulse code modulation (DPCM).
- With channel coding, on the other hand, a noticeable improvement in the transmission behavior is achieved by using a redundancy specifically added at the transmitter to detect and correct transmission errors at the receiver end. Such codes, the most important of which are block codes, convolutional codes and turbo codes, are particularly important in the case of heavily disturbed channels. The greater the relative redundancy of the coded signal, the better the correction properties of the code, albeit at a reduced user data rate.
- Transmission coding – often referred to as line coding – is used to adapt the transmitted signal to the spectral characteristics of the transmission channel and receiving equipment by recoding the source symbols. For example, in the case of a channel with the frequency response characteristic $H_{\rm K}(f=0) = 0$, over which consequently no DC signal can be transmitted, transmission coding must ensure that the code symbol sequence contains neither a long $\rm L$ sequence nor a long $\rm H$ sequence.
In the current book "Digital Signal Transmission" we deal exclusively with this last, transmission-technical aspect.
- Channel Coding has its own book dedicated to it in our learning tutorial.
- Source coding is covered in detail in the book Information Theory (main chapter 2).
- Also voice coding described in the book "Examples of Communication Systems" is a special form of source coding.
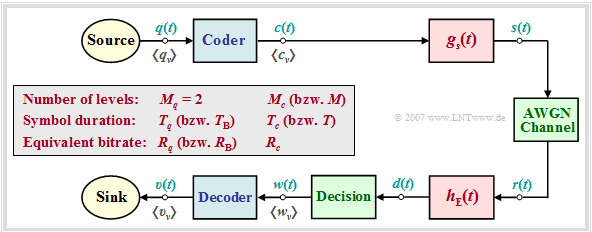
System model and description variables
In the following we always assume the block diagram sketched below and the following agreements:
- Let the digital source signal $q(t)$ be binary $(M_q = 2)$ and redundancy-free $(H_q = 1 \ \rm bit/symbol)$.
- With the symbol duration $T_q$ results for the symbol rate of the source:
- $$R_q = {H_{q}}/{T_q}= {1}/{T_q}\hspace{0.05cm}.$$
- Because of $M_q = 2$, in the following we also refer to $T_q$ as the bit duration and $R_q$ as the bit rate.
- For the comparison of transmission systems with different coding, $T_q$ and $R_q$ are always assumed to be constant.
Note: In later chapters we use $T_{\rm B}$ and $R_{\rm B}$ for this purpose. - The encoder signal $c(t)$ and also the transmitted signal $s(t)$ after pulse shaping with $g_s(t)$ have the step number $M_c$, the symbol duration $T_c$ and the symbol rate $1/T_c$. The equivalent bit rate is
- $$R_c = {{\rm log_2} (M_c)}/{T_c} \hspace{0.05cm}.$$
- It is always $R_c \ge R_q$, where the equal sign is valid only for the redundancy-free codes $(r_c = 0)$. Otherwise, we obtain for the relative code redundancy:
- $$r_c =({R_c - R_q})/{R_c} = 1 - R_q/{R_c} \hspace{0.05cm}.$$
Notes on nomenclature:
- In the context of transmission codes, $R_c$ in our learning tutorial always indicates the equivalent bit rate of the encoder signal has the unit "bit/s", as does the source bit rate $R_q$.
- In the literature on channel coding, in particular, $R_c$ is often used to denote the dimensionless code rate $1 - r_c$ . $R_c = 1 $ then indicates a redundancy-free code, while $R_c = 1/3 $ indicates a code with the relative redundancy $r_c = 2/3 $.
$\text{Example 2:}$ In the so-called 4B3T codes, four binary symbols $(m_q = 4, \ M_q= 2)$ are each represented by three ternary symbols $(m_c = 3, \ M_c= 3)$. Because of $4 \cdot T_q = 3 \cdot T_c$ holds:
- $$R_q = {1}/{T_q}, \hspace{0.1cm} R_c = { {\rm log_2} (3)} \hspace{-0.05cm} /{T_c} = {3/4 \cdot {\rm log_2} (3)} \hspace{-0.05cm}/{T_q}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}r_c =3/4\cdot {\rm log_2} (3) \hspace{-0.05cm}- \hspace{-0.05cm}1 \approx 15.9\, \% \hspace{0.05cm}.$$
More detailed information about the 4B3T codes can be found in the chapter of the same name .
ACF calculation of a digital signal
To simplify the notation, $M_c = M$ and $T_c = T$ is set in the following. Thus, for the transmitted signal $s(t)$ in the case of an unlimited-time message sequence with $a_\nu \in \{ a_1,$ ... , $a_M\}$ can be written:
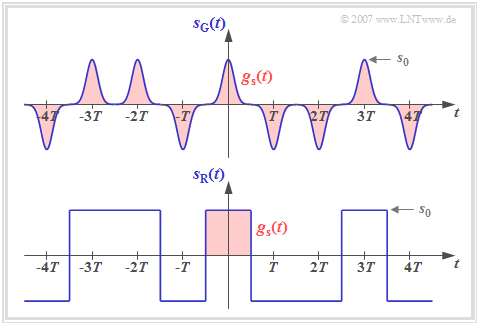
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.$$
This signal representation includes both the source statistics $($amplitude coefficients $a_\nu$) and the transmitted pulse shape $g_s(t)$. The diagram shows two binary bipolar transmitted signals $s_{\rm G}(t)$ and $s_{\rm R}(t)$ with the same amplitude coefficients $a_\nu$, which thus differ only by the basic transmission pulse $g_s(t)$.
It can be seen from this representation that a digital signal is generally nonstationary:
- For the transmitted signal $s_{\rm G}(t)$ with narrow Gaussian pulses, the non-stationarity is obvious, since, for example, at multiples of $T$ the variance is $\sigma_s^2 = s_0^2$, while exactly in between $\sigma_s^2 \approx 0$ holds.
- Also the signal $s_{\rm R}(t)$ with NRZ rectangular pulses is non–stationary in a strict sense, because here the moments at the bit boundaries differ with respect to all other instants. For example, $s_{\rm R}(t = \pm T/2)=0$.
$\text{Definition:}$ A random process whose moments $m_k(t) = m_k(t+ \nu \cdot T)$ repeat periodically with $T$ is called cyclostationary; $k$ and $\nu$ have integer values in this implicit definition.
Many of the rules valid for ergodic processes can also be applied to cycloergodic (and hence to cyclostationary ) processes with only minor restrictions.
In particular, for the auto-correlation function (ACF) of such random processes with sample signal $s(t)$ holds:
- $$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] \hspace{0.05cm}.$$
With the above equation of the transmitted signal, the ACF as a time average can also be written as follows:
- $$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}\frac{1}{T} \cdot \lim_{N \to \infty} \frac{1}{2N +1} \cdot \sum_{\nu = -N}^{+N} a_\nu \cdot a_{\nu + \lambda} \cdot \int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau - \lambda \cdot T)\,{\rm d} t \hspace{0.05cm}.$$
Since the limit, integral and sum may be interchanged, with the substitutions $N = T_{\rm M}/(2T)$, $\lambda = \kappa- \nu$ and $t - \nu \cdot T \to T$ for this can also be written:
- $$\varphi_s(\tau) = \lim_{T_{\rm M} \to \infty}\frac{1}{T_{\rm M}} \cdot \int_{-T_{\rm M}/2}^{+T_{\rm M}/2} \sum_{\nu = -\infty}^{+\infty} \sum_{\kappa = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T ) \cdot a_\kappa \cdot g_s ( t + \tau - \kappa \cdot T ) \,{\rm d} t \hspace{0.05cm}.$$
Now the following quantities are introduced for abbreviation:
$\text{Definition:}$ The discrete ACF of the amplitude coefficients provides statements about the linear statistical bonds of the amplitude coefficients $a_{\nu}$ and $a_{\nu + \lambda}$ and has no unit:
- $$\varphi_a(\lambda) = \lim_{N \to \infty} \frac{1}{2N +1} \cdot \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot a_{\nu + \lambda} \hspace{0.05cm}.$$
$\text{Definition:}$ The energy ACF of the basic pulse is defined similarly to the general (power) ACF. It is marked with a dot. Since $g_s(t)$ is energy-limited, the division by $T_{\rm M}$ and the boundary transition can be omitted:
- $$\varphi^{^{\bullet} }_{gs}(\tau) = \int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau)\,{\rm d} t \hspace{0.05cm}.$$
$\text{Definition:}$ For the auto-correlation function of a digital signal $s(t)$ holds in general:
- $$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$
The signal $s(t)$ can be binary or multi-level, unipolar or bipolar as well as redundancy-free or redundant (line-coded). The pulse shape is taken into account by the energy ACF.
If the digital signal $s(t)$ describes a voltage waveform, the energy ACF of the basic pulse $g_s(t)$ has the unit $\rm V^2s$ and $\varphi_s(\tau)$ has the unit $\rm V^2$, each related to the resistor $1 \ \rm \Omega$.
Note: In the strict sense of system theory, one would have to define the ACF of the amplitude coefficients as follows:
- $$\varphi_{a , \hspace{0.08cm}\delta}(\tau) = \sum_{\lambda = -\infty}^{+\infty} \varphi_a(\lambda)\cdot \delta(\tau - \lambda \cdot T)\hspace{0.05cm}.$$
Thus, the above equation would be as follows:
- $$\varphi_s(\tau) ={1}/{T} \cdot \varphi_{a , \hspace{0.08cm} \delta}(\tau)\star \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$
For simplicity, the discrete ACF of amplitude coefficients
⇒ $\varphi_a(\lambda)$
is written without these Dirac delta functions in the following.
PSD calculation of a digital signal
The corresponding quantity to the auto-correlation function (ACF) of a random signal ⇒ $\varphi_s(\tau)$ in the frequency domain is the power-spectral density (PSD) ⇒ ${\it \Phi}_s(f)$, which is in a fixed relation with the ACF via the Fourier integral:
- $$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \tau} \,{\rm d} \tau \hspace{0.05cm}.$$
Considering the relation between energy ACF and energy spectrum,
- $$\varphi^{^{\hspace{0.05cm}\bullet}}_{gs}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{gs}(f) = |G_s(f)|^2 \hspace{0.05cm},$$
and the shifting theorem, the power-spectral density of the digital signal $s(t)$ can be represented in the following way:
- $${\it \Phi}_s(f) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot {\it \Phi}^{^{\hspace{0.05cm}\bullet}}_{gs}(f) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = {1}/{T} \cdot |G_s(f)|^2 \cdot \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot \cos ( 2 \pi f \lambda T)\hspace{0.05cm}.$$
Here it is considered that ${\it \Phi}_s(f)$ and $|G_s(f)|^2$ are real-valued and at the same time $\varphi_a(-\lambda) =\varphi_a(+\lambda)$ holds.
If we now define the spectral power density of the amplitude coefficients to be
- $${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda \hspace{0.02cm}T} = \varphi_a(0) + 2 \cdot \sum_{\lambda = 1}^{\infty}\varphi_a(\lambda)\cdot\cos ( 2 \pi f \lambda T) \hspace{0.05cm},$$
then the following expression is obtained:
- $${\it \Phi}_s(f) = {\it \Phi}_a(f) \cdot {1}/{T} \cdot |G_s(f)|^2 \hspace{0.05cm}.$$
$\text{Conclusion:}$ The power-spectral density ${\it \Phi}_s(f)$ of a digital signal $s(t)$ can be represented as the product of two functions:
- The first term ${\it \Phi}_a(f)$ is dimensionless and describes the spectral shaping of the transmitted signal by the statistical constraints of the source.
- In contrast, $\vert G_s(f) \vert^2$ takes into account the spectral shaping by the basic transmission pulse $g_s(t)$. The narrower this is, the broader is $\vert G_s(f) \vert^2$ and thus the larger is the bandwidth requirement.
- The energy spectrum has the unit $\rm V^2s/Hz$ and the power-spectral density – due to the division by the symbol distance $T$ – the unit $\rm V^2/Hz$. Both specifications are again only valid for the resistor $1 \ \rm \Omega$.
ACF and PSD for bipolar binary signals
The previous results are now illustrated by examples. Starting from binary bipolar amplitude coefficients $a_\nu \in \{-1, +1\}$, if there are no bonds between the individual amplitude coefficients $a_\nu$, we obtain:
- $$\varphi_a(\lambda) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}}\\ {\rm{for}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \lambda \ne 0 \\ \end{array} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\varphi_s(\tau)= {1}/{T} \cdot \varphi^{^{\bullet}}_{gs}(\tau)\hspace{0.05cm}.$$
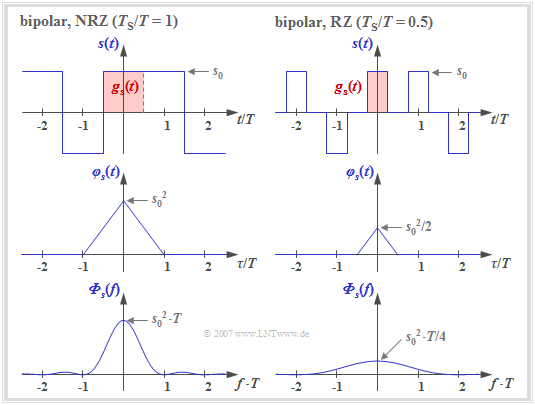
The graph shows two signal sections each with rectangular pulses $g_s(t)$, which accordingly lead to a triangular ACF and to a $\rm si^2$–shaped power-spectral density (PSD).
- The left pictures describe a NRZ signaling. That means: The width $T_{\rm S}$ of the basic pulse is equal to the distance $T$ of two transmitted pulses (source symbols).
- In contrast, the right pictures apply to an RZ pulse with the duty cycle $T_{\rm S}/T = 0.5$.
One can see from these representations:
- For NRZ rectangular pulses, the transmit power (referenced to the $1 \ \rm \Omega$ resistor) is $P_{\rm S} = \varphi_s(\tau = 0) = s_0^2$ and the triangular ACF is limited to the range $|\tau| \le T_{\rm S}= T$.
- The PSD ${\it \Phi}_s(f)$ as the Fourier transform of $\varphi_s(\tau)$ is $\rm si^2$–shaped with equidistant zeros at distance $1/T$. The area under the PSD curve again gives the transmit power $P_{\rm S} = s_0^2$.
- In the case of RZ signaling (right column), the triangular ACF is smaller in height and width by a factor of $T_{\rm S}/T = 0.5$, respectively, compared to the left image.
$\text{Conclusion:}$ If one compares the two power-spectral densities (lower pictures), one recognizes for $T_{\rm S}/T = 0.5$ (RZ pulse) compared to $T_{\rm S}/T = 1$ (NRZ pulse) a reduction in height by a factor of $4$ and a broadening by a factor of $2$. The area (power) is thus half as large, since in half the time $s(t) = 0$.
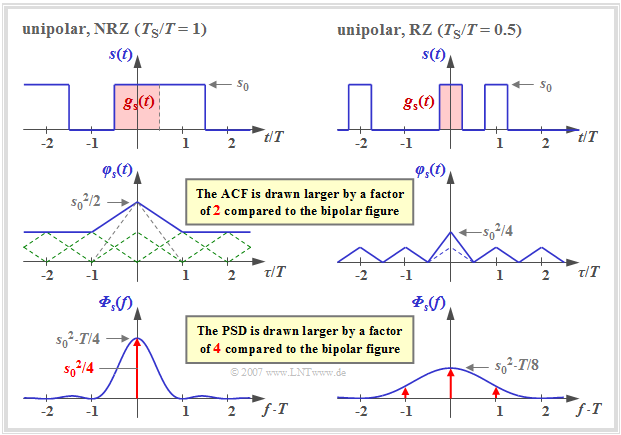
ACF and PSD for unipolar binary signals
We continue to assume NRZ or RZ rectangular pulses. But let the binary amplitude coefficients now be unipolar: $a_\nu \in \{0, 1\}$.
Then for the discrete ACF of the amplitude coefficients holds:
- $$\varphi_a(\lambda) = \left\{ \begin{array}{c} m_2 = 0.5 \\ \\ m_1^2 = 0.25 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}}\\ \\ {\rm{for}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \\ \lambda \ne 0 \hspace{0.05cm}.\\ \end{array}$$
Assumed here are equal probability amplitude coefficients ⇒ ${\rm Pr}(a_\nu =0) = {\rm Pr}(a_\nu =1) = 0.5$ with no statistical ties, so that both the quadratic mean $m_2$ (power) and the linear mean $m_1$ (DC component) are $0.5$, respectively.
The graph shows a signal section, the ACF and the PSD with unipolar amplitude coefficients,
- left for rectangular NRZ pulses $(T_{\rm S}/T = 1)$ , and
- right for RZ pulses with duty cycle $T_{\rm S}/T = 0.5$.
There are the following differences compared to bipolar signaling:
- Durch die Addition der unendlich vielen Dreieckfunktionen im Abstand $T$, alle mit gleicher Höhe, ergibt sich für die ACF in der linken Grafik (NRZ) ein konstanter Gleichanteil $s_0^2/4$.
- Daneben verbleibt im Bereich $|\tau| \le T_{\rm S}$ ein einzelnes Dreieck ebenfalls mit Höhe $s_0^2/4$, das im Leistungsdichtespektrum (PSD) zum $\rm si^2$–förmigen Verlauf führt (blaue Kurve).
- Der Gleichanteil in der ACF hat im PSD eine Diracfunktion bei der Frequenz $f = 0$ mit dem Gewicht $s_0^2/4$ zur Folge. Dadurch wird der PSD–Wert ${\it \Phi}_s(f=0)$ unendlich groß.
Aus der rechten Grafik – gültig für $T_{\rm S}/T = 0.5$ – erkennt man, dass sich nun die ACF aus einem periodischen Dreiecksverlauf (im mittleren Bereich gestrichelt eingezeichnet) und zusätzlich noch aus einem einmaligen Dreieck im Bereich $|\tau| \le T_{\rm S} = T/2$ mit Höhe $s_0^2/8$ zusammensetzt.
- Diese einmalige Dreieckfunktion führt zum kontinuierlichen, $\rm si^2$–förmigen Anteil (blaue Kurve) von ${\it \Phi}_s(f)$ mit der ersten Nullstelle bei $1/T_{\rm S} = 2/T$.
- Dagegen führt die periodische Dreieckfunktion nach den Gesetzmäßigkeiten der Fourierreihe zu einer unendlichen Summe von Diracfunktionen mit unterschiedlichen Gewichten im Abstand $1/T$ (rot gezeichnet).
- Die Gewichte der Diracfunktionen sind proportional zum kontinuierlichen (blauen) PSD–Anteil. Das maximale Gewicht $s_0^2/8$ besitzt die Diraclinie bei $f = 0$. Dagegen sind die Diraclinien bei $\pm 2/T$ und Vielfachen davon nicht vorhanden bzw. besitzen jeweils das Gewicht $0$, da hier auch der kontinuierliche PSD–Anteil Nullstellen besitzt.
$\text{Hinweis:}$
- Unipolare Amplitudenkoeffizienten treten zum Beispiel bei optischen Übertragungssystemen auf.
- In späteren Kapiteln beschränken wir uns aber meist auf die bipolare Signalisierung.
Aufgaben zum Kapitel
Aufgabe 2.1: AKF und LDS nach Codierung
Aufgabe 2.1Z: Zur äquivalenten Bitrate
Aufgabe: 2.2 Binäre bipolare Rechtecke