Difference between revisions of "Digital Signal Transmission/Intersymbol Interference for Multi-Level Transmission"
| Line 6: | Line 6: | ||
}} | }} | ||
| − | == | + | == Eye opening for redundancy-free multi-level systems== |
<br> | <br> | ||
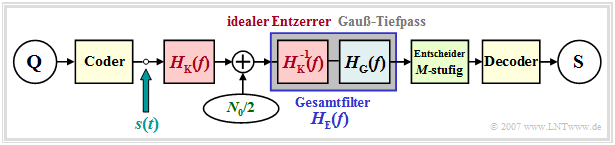
| − | [[File:P ID1411 Dig T 3 4 S1a version1.png|right|frame| | + | [[File:P ID1411 Dig T 3 4 S1a version1.png|right|frame|Block diagram for a multi-level/coded transmission system|class=fit]] |
| − | + | We further assume the following: | |
| − | *NRZ | + | *NRZ rectangular transmitted pulses,<br> |
| − | * | + | *coaxial cable and AWGN noise,<br> |
| − | * | + | *ideal channel equalization, and<br> |
| − | * | + | *a Gaussian low-pass filter for noise power limitation.<br><br> |
| − | + | In contrast to the [[Digital_Signal_Transmission/Berücksichtigung_von_Kanalverzerrungen_und_Entzerrung|last chapter]], the still redundancy-free transmitted signal $s(t)$ is now no longer binary, but $M$–level, which only has an effect in the set of values of the amplitude coefficients: | |
| − | :$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.3cm}{\rm | + | :$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.3cm}{\rm with}\hspace{0.3cm} |
a_\nu \in \{ a_1,\ \text{ ...} \ , a_\mu , \ \text{ ...} \ , a_{M}\}\hspace{0.05cm}.$$ | a_\nu \in \{ a_1,\ \text{ ...} \ , a_\mu , \ \text{ ...} \ , a_{M}\}\hspace{0.05cm}.$$ | ||
| − | + | Accordingly, the decision now has not only one, but $M-1$ decision thresholds and in the eye diagram $M-1$ eye openings are visible when the eye is open.<br> | |
| − | + | Comparing the eye diagrams (without noise) | |
| − | * | + | *of a binary $(M = 2)$,<br> |
| − | * | + | *of a ternary $(M = 3)$, und<br> |
| − | * | + | *a quaternary $(M = 4)$ |
| − | + | transmission system with the same basic transmitter pulse $g_d(t)$ and the same symbol duration $T$, one obtains for the half vertical eye opening in general: | |
:$${\ddot{o}(T_{\rm D})}/{ 2} = \frac{g_0}{ M-1} - \sum_{\nu = 1}^{\infty} |g_{-\nu} | - \sum_{\nu = 1}^{\infty} |g_{\nu} |\hspace{0.05cm}.$$ | :$${\ddot{o}(T_{\rm D})}/{ 2} = \frac{g_0}{ M-1} - \sum_{\nu = 1}^{\infty} |g_{-\nu} | - \sum_{\nu = 1}^{\infty} |g_{\nu} |\hspace{0.05cm}.$$ | ||
| − | + | Here $g_0 = g_d(t= 0)$ denotes the ''main value'' as in the chapter [[Digital_Signal_Transmission/Berücksichtigung_von_Kanalverzerrungen_und_Entzerrung|Consideration of Channel Distortion and Equalization]]. The two sums in the above equation take into account | |
| − | * | + | *the ''precursors'' $g_1$, $g_2$, ... of the trailing pulses (second term), and |
| − | * | + | *the ''trailers'' $g_{-1}$, $g_{-2}$, ... of the preceding pulses (last term). |
| − | + | Here, $g_\nu = g_d(t = \nu \cdot T)$ always holds. | |
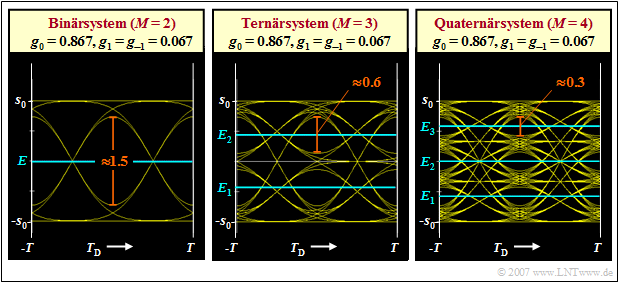
| − | [[File:P ID1412 Dig T 3 4 S1b version1.png|right|frame| | + | [[File:P ID1412 Dig T 3 4 S1b version1.png|right|frame|Eye diagrams of a binary, ternary and quaternary system|class=fit]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ Below you can see three eye diagrams for the level numbers $M = 2$, $M = 3$ and $M = 4$. |
| − | * | + | *The binary eye diagram is valid for a Gaussian low-pass with the (normalized) cutoff frequency $f_{\rm G} \cdot T = 0.6$. With the main value $g_0 = 0.867 \cdot s_0$ and the two outliers $g_{1} = 0.067 \cdot s_0$ and $g_{-1} = g_{1}$, the result in this case for the vertical eye opening (rounding to one decimal place) is: |
:$${\ddot{o}(T_{\rm D})}= 2 \cdot (g_0 - 2 \cdot g_1) \approx 1.5 \cdot s_0 \hspace{0.05cm}.$$ | :$${\ddot{o}(T_{\rm D})}= 2 \cdot (g_0 - 2 \cdot g_1) \approx 1.5 \cdot s_0 \hspace{0.05cm}.$$ | ||
| − | * | + | *In the multi-level systems, the eye opening per se is smaller by a factor of $1/(M-1)$. Thus, the eye opening is reduced (relatively speaking) more by the (equally large) leading and trailing elements than in the binary system. One obtains with the same basic pulse values for |
:$$M = 3\text{:} \hspace{0.2cm}{\ddot{o}(T_{\rm D})} = 2 \cdot (g_0/2 - 2 \cdot g_1) \approx 0.6 \cdot s_0 | :$$M = 3\text{:} \hspace{0.2cm}{\ddot{o}(T_{\rm D})} = 2 \cdot (g_0/2 - 2 \cdot g_1) \approx 0.6 \cdot s_0 | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| Line 51: | Line 51: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | It should be noted that the normalized cutoff frequency $f_{\rm G} \cdot T = 0.6$ is also the basis for these two multi-level systems. | |
| − | * | + | *When comparing the systems, however, it should be noted that the larger number of levels also increases the information flow. |
| − | * | + | *That is, the multi-level systems are better than these graphs indicate. More about this in the next section.}}<br> |
| − | == | + | == Comparison between binary and quaternary system== |
<br> | <br> | ||
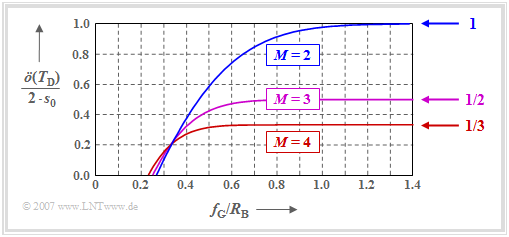
| − | [[File:P ID3140 Dig T 3 4 S2 version1.png|right|frame| | + | [[File:P ID3140 Dig T 3 4 S2 version1.png|right|frame|Half normalized eye opening for $M = 2$, $M = 3$ $M = 2$ and $M = 4$|class=fit]] |
| − | + | The comparison made in the last section is not fair because the information flow was not assumed to be the same. A system comparison at constant equivalent bit rate $R_{\rm B}$ must rather also take into account that in the (redundancy-free) multi-level systems the symbol duration $T$ is larger by a factor $\log_2 \ (M)$ than in the binary system, which has a favorable effect on the intersymbol interferences.<br> | |
<br clear=all> | <br clear=all> | ||
| − | + | The graph shows the half eye opening (normalized to $s_0$ ) as a function of the quotient $f_{\rm G}/R_{\rm B}$ of the Gaussian receiver filter. In [[Aufgaben:Aufgabe_3.4Z:_Augenöffnung_und_Stufenzahl|Aufgabe 3.4Z]], this is calculated in analytical form as follows: | |
:$$\ddot{o}_{\rm norm} = \frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = \frac{M}{ M-1}\cdot \frac{g_0}{ | :$$\ddot{o}_{\rm norm} = \frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = \frac{M}{ M-1}\cdot \frac{g_0}{ | ||
s_0} -1 = \frac{1}{ M-1}\cdot \big [1- 2 \cdot M \cdot {\rm Q} \left( | s_0} -1 = \frac{1}{ M-1}\cdot \big [1- 2 \cdot M \cdot {\rm Q} \left( | ||
| Line 68: | Line 68: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | One can see from the above graph: | |
| − | * | + | *For broadband filter $($that is: for large $f_{\rm G})$ the binary system is clearly superior to the multi-level systems. The normalized half eye opening in the limiting case is $\ddot{o}_{\rm norm} = 1$ (for $M = 2$), $\ddot{o}_{\rm norm} = 1/2$ (for $M = 3$) and $\ddot{o}_{\rm norm} = 1/3$ (for $M = 4$).<br> |
| − | * | + | *As shown in the graph, for cutoff frequencies $f_{\rm G}/R_{\rm B} < 0.35$, the level number $M=4$ (red curve) leads to a larger eye opening than $M=2$ (blue curve). The ternary system $(M=3$, purple curve$)$ lies almost in the entire range between binary and quaternary systems.<br> |
| − | * | + | *It should also be mentioned that for the quaternary system, a closed eye results only with a cutoff frequency $f_{\rm G}/R_{\rm B} < 0.23$ (which leads to very large error probabilities), while a practically relevant binary transmission is already no longer possible for $f_{\rm G}/R_{\rm B} < 0.27$. <br> |
| − | == | + | == Comparison of the optimal cutoff frequencies == |
<br> | <br> | ||
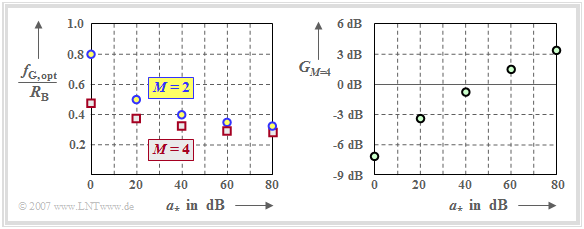
| − | [[File:P ID1414 Dig T 3 4 S3 version1.png|right|frame| | + | [[File:P ID1414 Dig T 3 4 S3 version1.png|right|frame|Optimal cutoff frequency for $M=2$ and $M=4$ ; signal-to-noise ratio gain due to $M=4$ |class=fit]] |
| − | + | We now compare the optimal cutoff frequencies of the Gaussian filter, which result for $M=2$ and $M=4$, respectively. The comparison is based on a coaxial transmission channel with the characteristic cable attenuation $a_\star$. The larger this channel parameter is (which also means: the longer the cable is), the more the noise is amplified by the required equalization at the receiver.<br> | |
| − | + | Let's interpret the left graph first: | |
| − | * | + | *With distortion-free channel $(a_\star = 0 \ \rm dB)$ the (normalized) optimal cutoff frequencies result to $f_\text{G, opt}/R_{\rm B} = 0.8$ $($for $M=2)$ and $f_\text{G, opt}/R_{\rm B} = 0.48$ $($for $M=4)$. According to the [[Digital_Signal_Transmission/Impulsinterferenzen_bei_mehrstufiger_Übertragung#Vergleich_zwischen_Bin.C3.A4r.E2.80.93_und_Quatern.C3.A4rsystem| curve "half normalized eye opening"]] in the last section, the binary system is clearly superior to the quaternary system.<br> |
*Mit der charakteristischen Kabeldämpfung $a_\star = 80 \ \rm dB$ erhält man für das Binärsystem $(M=2)$ die optimale Grenzfrequenz $f_\text{G, opt}/R_{\rm B} = 0.33$. Für das Quaternärsystem $(M=4)$ ergibt sich wieder ein kleinerer Wert: $f_\text{G, opt}/R_{\rm B} = 0.28$. | *Mit der charakteristischen Kabeldämpfung $a_\star = 80 \ \rm dB$ erhält man für das Binärsystem $(M=2)$ die optimale Grenzfrequenz $f_\text{G, opt}/R_{\rm B} = 0.33$. Für das Quaternärsystem $(M=4)$ ergibt sich wieder ein kleinerer Wert: $f_\text{G, opt}/R_{\rm B} = 0.28$. | ||
Revision as of 16:32, 2 May 2022
Contents
Eye opening for redundancy-free multi-level systems
We further assume the following:
- NRZ rectangular transmitted pulses,
- coaxial cable and AWGN noise,
- ideal channel equalization, and
- a Gaussian low-pass filter for noise power limitation.
In contrast to the last chapter, the still redundancy-free transmitted signal $s(t)$ is now no longer binary, but $M$–level, which only has an effect in the set of values of the amplitude coefficients:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.3cm}{\rm with}\hspace{0.3cm} a_\nu \in \{ a_1,\ \text{ ...} \ , a_\mu , \ \text{ ...} \ , a_{M}\}\hspace{0.05cm}.$$
Accordingly, the decision now has not only one, but $M-1$ decision thresholds and in the eye diagram $M-1$ eye openings are visible when the eye is open.
Comparing the eye diagrams (without noise)
- of a binary $(M = 2)$,
- of a ternary $(M = 3)$, und
- a quaternary $(M = 4)$
transmission system with the same basic transmitter pulse $g_d(t)$ and the same symbol duration $T$, one obtains for the half vertical eye opening in general:
- $${\ddot{o}(T_{\rm D})}/{ 2} = \frac{g_0}{ M-1} - \sum_{\nu = 1}^{\infty} |g_{-\nu} | - \sum_{\nu = 1}^{\infty} |g_{\nu} |\hspace{0.05cm}.$$
Here $g_0 = g_d(t= 0)$ denotes the main value as in the chapter Consideration of Channel Distortion and Equalization. The two sums in the above equation take into account
- the precursors $g_1$, $g_2$, ... of the trailing pulses (second term), and
- the trailers $g_{-1}$, $g_{-2}$, ... of the preceding pulses (last term).
Here, $g_\nu = g_d(t = \nu \cdot T)$ always holds.
$\text{Example 1:}$ Below you can see three eye diagrams for the level numbers $M = 2$, $M = 3$ and $M = 4$.
- The binary eye diagram is valid for a Gaussian low-pass with the (normalized) cutoff frequency $f_{\rm G} \cdot T = 0.6$. With the main value $g_0 = 0.867 \cdot s_0$ and the two outliers $g_{1} = 0.067 \cdot s_0$ and $g_{-1} = g_{1}$, the result in this case for the vertical eye opening (rounding to one decimal place) is:
- $${\ddot{o}(T_{\rm D})}= 2 \cdot (g_0 - 2 \cdot g_1) \approx 1.5 \cdot s_0 \hspace{0.05cm}.$$
- In the multi-level systems, the eye opening per se is smaller by a factor of $1/(M-1)$. Thus, the eye opening is reduced (relatively speaking) more by the (equally large) leading and trailing elements than in the binary system. One obtains with the same basic pulse values for
- $$M = 3\text{:} \hspace{0.2cm}{\ddot{o}(T_{\rm D})} = 2 \cdot (g_0/2 - 2 \cdot g_1) \approx 0.6 \cdot s_0 \hspace{0.05cm},$$
- $$M = 4\text{:} \hspace{0.2cm}{\ddot{o}(T_{\rm D})} = 2 \cdot (g_0/3 - 2 \cdot g_1) \approx 0.3 \cdot s_0 \hspace{0.05cm}.$$
It should be noted that the normalized cutoff frequency $f_{\rm G} \cdot T = 0.6$ is also the basis for these two multi-level systems.
- When comparing the systems, however, it should be noted that the larger number of levels also increases the information flow.
- That is, the multi-level systems are better than these graphs indicate. More about this in the next section.
Comparison between binary and quaternary system
The comparison made in the last section is not fair because the information flow was not assumed to be the same. A system comparison at constant equivalent bit rate $R_{\rm B}$ must rather also take into account that in the (redundancy-free) multi-level systems the symbol duration $T$ is larger by a factor $\log_2 \ (M)$ than in the binary system, which has a favorable effect on the intersymbol interferences.
The graph shows the half eye opening (normalized to $s_0$ ) as a function of the quotient $f_{\rm G}/R_{\rm B}$ of the Gaussian receiver filter. In Aufgabe 3.4Z, this is calculated in analytical form as follows:
- $$\ddot{o}_{\rm norm} = \frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = \frac{M}{ M-1}\cdot \frac{g_0}{ s_0} -1 = \frac{1}{ M-1}\cdot \big [1- 2 \cdot M \cdot {\rm Q} \left( \sqrt{2\pi} \cdot {\log_2}\hspace{0.1cm}(M) \cdot {f_{\rm G}}/{R_{\rm B}} \right)\big] \hspace{0.05cm}.$$
One can see from the above graph:
- For broadband filter $($that is: for large $f_{\rm G})$ the binary system is clearly superior to the multi-level systems. The normalized half eye opening in the limiting case is $\ddot{o}_{\rm norm} = 1$ (for $M = 2$), $\ddot{o}_{\rm norm} = 1/2$ (for $M = 3$) and $\ddot{o}_{\rm norm} = 1/3$ (for $M = 4$).
- As shown in the graph, for cutoff frequencies $f_{\rm G}/R_{\rm B} < 0.35$, the level number $M=4$ (red curve) leads to a larger eye opening than $M=2$ (blue curve). The ternary system $(M=3$, purple curve$)$ lies almost in the entire range between binary and quaternary systems.
- It should also be mentioned that for the quaternary system, a closed eye results only with a cutoff frequency $f_{\rm G}/R_{\rm B} < 0.23$ (which leads to very large error probabilities), while a practically relevant binary transmission is already no longer possible for $f_{\rm G}/R_{\rm B} < 0.27$.
Comparison of the optimal cutoff frequencies
We now compare the optimal cutoff frequencies of the Gaussian filter, which result for $M=2$ and $M=4$, respectively. The comparison is based on a coaxial transmission channel with the characteristic cable attenuation $a_\star$. The larger this channel parameter is (which also means: the longer the cable is), the more the noise is amplified by the required equalization at the receiver.
Let's interpret the left graph first:
- With distortion-free channel $(a_\star = 0 \ \rm dB)$ the (normalized) optimal cutoff frequencies result to $f_\text{G, opt}/R_{\rm B} = 0.8$ $($for $M=2)$ and $f_\text{G, opt}/R_{\rm B} = 0.48$ $($for $M=4)$. According to the curve "half normalized eye opening" in the last section, the binary system is clearly superior to the quaternary system.
- Mit der charakteristischen Kabeldämpfung $a_\star = 80 \ \rm dB$ erhält man für das Binärsystem $(M=2)$ die optimale Grenzfrequenz $f_\text{G, opt}/R_{\rm B} = 0.33$. Für das Quaternärsystem $(M=4)$ ergibt sich wieder ein kleinerer Wert: $f_\text{G, opt}/R_{\rm B} = 0.28$.
Das optimierte Binärsystem ist aber trotz größerer Augenöffnung nicht immer besser als das optimierte Quaternärsystem, da auch die Rauschleistung zu berücksichtigen ist. Diese wird mit kleiner werdenden Grenzfrequenz ebenfalls kleiner.
Die rechte Grafik zeigt den Störabstandsgewinn des Quaternärsystems gegenüber dem Binärsystem,
- $$G_{_{M=4}} = 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{_{{\rm U},\hspace{0.05cm} M=4}} - 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{_{{\rm U}, \hspace{0.05cm}M=2}},$$
wenn die Grenzfrequenzen gemäß der linken Grafik jeweils optimal gewählt werden. Demnach gilt:
- Für $a_\star <50 \ \rm dB$ ist das Binärsystem optimal. Beim verzerrungsfreien Kanal $(a_\star = 0 \ \rm dB)$ ergibt sich ein um ca. $7 \ \rm dB$ größeres SNR als mit $M=4$.
- Dagegen ergeben sich für $a_\star >50 \ \rm dB$ mit $M=4$ günstigere Verhältnisse. Bei $a_\star = 80 \ \rm dB$ ist der Störabstandsgewinn gegenüber $M=2$ größer als $3 \ \rm dB$.
Eye opening for the pseudo ternary codes
Im Kapitel Symbolweise Codierung wurden die Pseudoternärcodes allgemein beschrieben und es wurden für diese die Augendiagramme bei Nyquistimpulsformung angegeben.
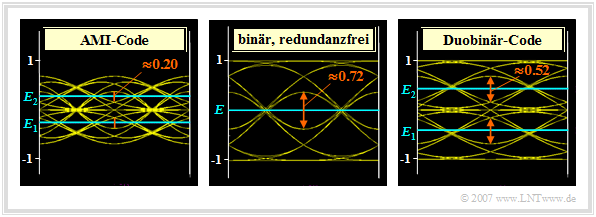
In nebenstehender Grafik sehen Sie im Vergleich zum redundanzfreien Binärcode (Mitte) die Augendiagramme – jeweils ohne Rauschen – für
- den AMI–Code (links),
- den Duobinärcode (rechts).
Die Amplitude ist jeweils $s_0 = 1$. Alle Augendiagramme gelten zudem für ein gaußförmiges Empfangsfilter mit der Grenzfrequenz $f_\text{G} \cdot T = 0.4$, woraus sich folgende (normierte) Grundimpulswerte ergeben:
- $$g_{0} \approx 0.68, \hspace{0.2cm} g_{1}= g_{-1} \approx 0.16, \hspace{0.2cm}\hspace{0.2cm} g_{2}= g_{-2}= \text{...} \approx 0 \hspace{0.05cm}.$$
Beim redundanzfreien Binärsystem (mittlere Grafik) erhält man somit aufgrund der Impulsinterferenzen für die Augenöffnung
- $${\ddot{o}(T_{\rm D})}= 2 \cdot (g_0 - 2 \cdot g_1 ) = 0.72 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \ddot{o}_{\rm norm} = \frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = 36\%$$
im Vergleich zu $\ddot{o}(T_{\rm D}) = 2$ bzw. $\ddot{o}_{\rm norm} = 100\%$ beim binären Nyquistsystem.
Bei den Pseudoternärcodes gibt es jeweils zwei Augenöffnungen und man benötigt für die ternäre Entscheidung zwei Schwellenwerte $E_1$ und $E_2$. Da alle Pseudoternärcodes zudem mit der gleichen Symbolrate arbeiten wie das redundanzfreie Binärsystem,
- sind die Detektionsgrundimpulswerte $g_\nu$ und auch der Rauscheffektivwert $\sigma_d$ in beiden Fällen gleich,
- ist die (halbe) Augenöffnung für die Systemoptimierung ebenso geeignet wie das ungünstigste S/N–Verhältnis $\rho_{\rm U} = [\ddot{o}(T_{\rm D})/2]^2 /\sigma_d^2$ und die daraus resultierende Worst–Case–Fehlerwahrscheinlichkeit $p_{\rm U}$.
Interpretieren wir nun das (linke) Augendiagramm bei AMI–Codierung:
- Die obere Begrenzung des oberen Auges gehört zur Symbolfolge "$\text{...} -\hspace{-0.05cm}1,\hspace{0.05cm} {\it +\hspace{-0.05cm}1},\hspace{0.05cm} -\hspace{-0.05cm}\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$" (Koeffizient $a_{\nu = 0}$ kursiv) und liegt demzufolge bei $d_{\rm oben} = g_0 - 2\cdot g_1$.
- Die untere Begrenzungslinie $d_{\rm unten} = g_1$ geht auf die Symbolfolge "$\text{...} 0,\hspace{0.05cm} {\it 0},\hspace{0.05cm} +\hspace{-0.05cm}\hspace{-0.05cm}1 \text{...}$" bzw. auf die Folge "$\text{...} +\hspace{-0.05cm}\hspace{-0.05cm}1,\hspace{0.05cm} {\it 0},\hspace{0.05cm} 0\hspace{0.05cm} \text{...}$" zurück. Hierbei ist berücksichtigt, dass die Folge "$\text{...} +\hspace{-0.05cm}\hspace{-0.05cm}1,\hspace{0.05cm} {\it 0},\hspace{0.05cm} +\hspace{-0.05cm}\hspace{-0.05cm}1\hspace{0.05cm} \text{...}$" durch die AMI–Codierregel ausgeschlossen wird.
- Damit gilt für die Augenöffnung des AMI–Codes:
- $${\ddot{o}(T_{\rm D})}= d_{\rm oben} - d_{\rm unten} =g_0 - 3 \cdot g_1 = 0.20 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \ddot{o}_{\rm norm} = \frac{\ddot{o}(T_{\rm D})}{ 2 \cdot s_0} = 10\, \%.$$
- Die obere Entscheiderschwelle $E_2$ sowie die untere Entscheiderschwelle $E_1$ liegen bei
- $$E_2 = {1}/{2} \cdot (d_{\rm oben} + d_{\rm unten}) = {1}/{2} \cdot (g_0 - g_1) = 0.27 \hspace{0.05cm}, \hspace{0.2cm}E_1 = - 0.27 \hspace{0.05cm}.$$
Beim Duobinärcode (rechte Grafik) tritt die besonders ungünstige alternierende Symbolfolge nicht auf und man erhält für die Augenöffung sowie die Entscheiderschwellen:
- $$d_{\rm oben}= g_0, \hspace{0.2cm} d_{\rm unten} = g_1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})} = g_0 - g_1 = 0.52 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \ddot{o}_{\rm norm} = 26\, \% \hspace{0.05cm}, \hspace{0.3cm} E_2 = {1}/{2} \cdot (g_0 + g_1) = 0.42 \hspace{0.05cm}, \hspace{0.2cm}E_1 = - 0.42 \hspace{0.05cm}.$$
Hinweis: Die Degradationen durch Impulsinterferenzen bei AMI– und Duobinärcodierung können ebenfalls mit dem interaktiven Applet Augendiagramm und Augenöffnung angezeigt werden. Die angegebenen Fehlerwahrscheinlichkeiten gelten allerdings nur für den verzerrungsfreien Kanal $(a_\star = 0 \ \rm dB)$.
Grenzfrequenzoptimierung bei Pseudoternärcodierung
Unter Berücksichtigung eines koaxialen Übertragungskanals und der damit notwendigen Kanalentzerrung sind folgende Aussagen möglich:
- Der AMI–Code führt stets zu einem schlechteren Störabstand als der redundanzfreie Binärcode, wenn der Gesamtfrequenzgang gaußförmig verläuft. Mit der charakteristischen Kabeldämpfung $a_\star = 80 \ \rm dB$ beträgt der Störabstandsverlust ca. $11 \ \rm dB$.
- Dieser Verlust ist darauf zurückzuführen, dass trotz ternärer Codierung die Symbolrate gegenüber dem binären Vergleichssystem nicht vermindert wird. Dies hat zur Folge, dass beim AMI–Code bereits eine Grenzfrequenz $f_\text{G} \cdot T < 0.36$ zu einem geschlossenen Auge führt.
- Dagegen ergibt sich beim Duobinärcode ein geschlossenes Auge erst ab $f_\text{G} \cdot T < 0.22$. Dadurch ist auch die optimale Grenzfrequenz kleiner als beim Binärsystem. Bei 80 dB Kabeldämpfung ist der Duobinärcode in Kombination mit $f_\text{G} \cdot T =0.28$ um $3.3 \ \rm dB$ besser als der beste Wert bei redundanzfreier Binärcodierung.
$\text{Allerdings ist zu berücksichtigen:}$ Alle Ergebnisse in diesem Kapitel gelten unter der Bedingung $H_{\rm K}(f=0) = 1$.
- Soll ein redundanzfreies Signal oder das duobinär–codierte Signal über einen gleichsignalundurchlässigen Kanal übertragen werden, so ist eine aufwändige Gleichsignalwiedergewinnung erforderlich, die stets ebenfalls mit einer Degradation des S/N-Verhältnisses verbunden ist [ST85][1].
- Der AMI–Code ist gleichsignalfrei und kann damit auch über einen Telefonkanal ⇒ $H_{\rm K}(f=0) = 0$ übertragen werden. Dies ist der entscheidende Grund, warum der AMI–Code trotz ansonsten schlechter Eigenschaften zum Beispiel bei ISDN (Integrated Services Digital Network) eingesetzt wird.
Aufgaben zum Kapitel
Aufgabe 3.4: Grenzfrequenzoptimierung
Aufgabe 3.4Z: Augenöffnung und Stufenzahl
Aufgabe 3.5: Augenöffnung bei Pseudoternärcodierung
Quellenverzeichnis
- ↑ Söder, G.; Tröndle, K.: Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme. Berlin – Heidelberg: Springer, 1985.