Exercise 2.4: DSL/DMT with IDFT/DFT
A "realization form" of the $\rm DMT$ method (stands for Discrete Multitone Transmission) is based on the Inverse Discrete Fourier Transform $\rm (IDFT)$ at the transmitter and the Discrete Fourier Transform $\rm (DFT)$ at the receiver.
At the transmitter $N/2-1$ users are represented by the complex spectral coefficients $D_{k} \ (k = 1,$ ... , $N/2-1)$ allocated to the frequencies $f_{k} = k \cdot f_{0}$ . The fundamental frequency $f_{0}$ is the reciprocal of the symbol duration $T$.
- It holds $D_{k} \in \{ ±1 ± {\rm j} \}$ if one channel is allocated , in the other case $D_{k} = 0$.
- The coefficients $D_{0}$ and $D_{N/2}$ are always zero.
- The top coefficients are allocated conjugate-complex:
- $$D_k = D_{N-k}^{\star},\hspace{0.2cm}k = N/2 +1,\hspace{0.05cm} \text{...} \hspace{0.05cm}, N-1 \hspace{0.05cm}.$$
This ensures that the time signal $s(t)$ is always real. The sample values $s_{0}$, ... , $s_{N-1}$ of this signal are thereby formed by the IDFT, where the temporal distance of two samples is
- $$\Delta t = T/N = 1/(N \cdot f_{0}).$$
Low-pass filtering is used to obtain the continuous-time signal.
For ADSL/DMT, $N = 512$ and $f_{0} = 4.3125 \ \rm kHz$. In the example considered here, let the parameters be assumed as follows for simplicity:
- $$N = 16,\hspace{0.2cm}\delta t = 10\,{\rm µ s} \hspace{0.05cm}.$$
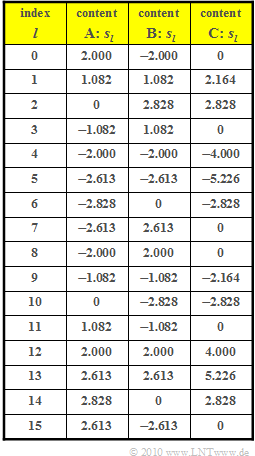
In the above table, for three different $D_{k}$ allocations, the sample values $s_{l} (l = 0$, ... , $15)$ according to the IDFT are given. The corresponding spectral coefficients $D_{k}\ (k = 0$, ... , $15)$ are sought.
Hints:
- This exercise belongs to the chapter "xDSL as Transmission Technology".
- The transmission signal for DSL has the form
- $$s(t) = \sum_{k = 1}^{K} \big [ 2 \cdot {\rm Re}\{D_k\} \cdot \cos(2\pi \cdot k f_0 \cdot t ) - 2 \cdot {\rm Im}\{D_k\} \cdot \sin(2\pi \cdot k f_0 \cdot t )\big ] \hspace{0.05cm}.$$
- Note also the following trigonometric relationship:
- $$\cos(2\pi f_0 t + \phi_0) = \cos( \phi_0) \cdot \cos(2\pi f_0 t ) - \sin( \phi_0) \cdot \sin(2\pi f_0 t ) \hspace{0.05cm}.$$
- The ratio of the maximum value and the rms value is called the crest factor' (or the crest factor) of a signal.
- You can check your solution with the interactive applet "Discrete Fourier Transform".
Questions
Solution
(2) The frame duration $T$ is given by $N \cdot \delta t = 0.16 \rm ms$.
- The fundamental frequency here is accordingly $f_{0} = 1/T = 6.25 \ \rm kHz$ and the total bandwidth is $B = 8 \cdot f_{0} \ \underline{= 50 \ \rm kHz}$.
- For comparison, for ADSL, this bandwidth results in $256 \cdot 4.3125 \ \rm kHz= 1104 \ kHz.$
(3) Correct is the second proposed solution:
- From the $16$ samples $s_{l}$ in the first column of the table $($allocation $\boldsymbol{\rm A})$ we see that $s(t)$ describes a harmonic oscillation with period $T_{0} = T$ (only one oscillation). The amplitude is equal to $2 \cdot \sqrt{2} =2.828$ and the phase is $\phi_0 = 45^\circ \ (π/4)$.
- Thus, for the continuous-time signal, we can write $($with $f_{0} = 1/T)$:
- $$s(t) = 2 \cdot \sqrt{2}\cdot \cos(2\pi f_0 t + \pi /4) \hspace{0.05cm}.$$
- With the given trigonometric transformation and ${\rm cos} \ (π/4) \ = \ {\rm sin} \ (π/4) \ = \ \sqrt{2}$ still holds:
- $$s(t) = 2 \cdot \cos(2\pi f_0 t ) - 2 \cdot \sin(2\pi f_0 t ) \hspace{0.05cm}.$$
- A coefficient comparison with the further equation.
- $$s(t) = \sum_{k = 1}^{K} \left [ 2 \cdot {\rm Re}[D_k] \cdot \cos(2\pi \cdot k f_0 \cdot t ) - 2 \cdot {\rm Im}[D_k] \cdot \sin(2\pi \cdot k f_0 \cdot t )\right ] \hspace{0.05cm}$$
- returns the result:
- $$2 \cdot {\rm Re}[D_1] = 2 \hspace{0.3cm} \ \Rightarrow \ \hspace{0.3cm} {\rm Re}[D_1] = 1\hspace{0.05cm},$$
- $$2 \cdot {\rm Im}[D_1] = 2 \hspace{0.3cm} \ \Rightarrow \ \hspace{0.3cm} {\rm Im}[D_1] = 1\hspace{0.05cm}.$$
- Further note that the coefficient $D_{15}$ is to be allocated the conjugate complex value:
- $$D_{15} = D_{1}^{\star} = 1 - {\rm j}\hspace{0.05cm}.$$
The same result would have been obtained by evaluating the (continuous-time) Fourier transform of $s(t)$:
- $$S(f) = (1 + {\rm j}) \cdot \delta (f - f_0) + (1 - {\rm j}) \cdot \delta (f + f_0)\hspace{0.05cm}.$$
The coefficient $D_1$ describes the weight at the first Dirac function (i.e., at $f = f_0$), and the coefficient $D_{15} = D_{-1}$ describes the weight of the Dirac function at $f = -f_0$. Here, the implicit periodic continuation in the DFT (or IDFT) should be noted.
(4) Correct is the proposed solution 3, where now $D_{13} = D_{3}^∗$ has to be considered.
- If one plots the samples $s_l$, one now recognizes the 3-fold frequency. For example, comparing $s_2$ and $s_{10}$ gives:
- $$8 \cdot \Delta t ={T}/{2} = 1.5 \cdot T_0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T_0 = {T}/{3}\hspace{0.05cm}.$$
- The amplitude is unchanged compared to the allocation $\boldsymbol{\rm A}$. The phase $\phi_0$ can be recognized from the first maximum at $l = 2$:
- $$ s(t) \ = \ 2 \cdot \sqrt{2}\cdot \cos(2\pi \cdot 3 f_0 \cdot ( t - 2 \cdot \delta t)) = \ 2 \cdot \sqrt{2}\cdot \cos(2\pi \cdot 3 f_0 \cdot t + \phi_0), \hspace{0.3cm} \phi_0 = 12 \pi \cdot \frac{\delta t}{T} = \frac{3 \pi}{4} \hspace{0.05cm}.$$
- Following the same procedure as in exercise (3), we now obtain $ {\rm cos}(3π/4) \ = \sin(3π/4) = -\sqrt{2}/2$:
- $${\rm Re}\{D_3\} = -1, \hspace{0.2cm} {\rm Im}\{D_3\} = -1\hspace{0.05cm}.$$
(5) The correct solution here is the first proposed solution:
- Due to the linearity of the IDFT, the coefficients $D_1$, $D_3$, $D_{13}$ and $D_{15}$ are obtained according to the results of the subtasks (4) and (5).
(6) The allocation $\boldsymbol{\rm C}$ leads to the sum of two harmonic oscillations (with $f_0$ and $3f_0$, respectively), each with the same amplitude $A$. Thus, the average signal power is given by:
- $$P_{\rm S} = 2 \cdot \frac{A^2}{2} = A^2 = 8\hspace{0.05cm}.$$
The rms value is equal to the square root of the transmitted power $P_{\rm S}$:
- $$s_{\rm eff} = \sqrt{P_{\rm S}} = A = 2.828\hspace{0.05cm}.$$
The maximum value can be read from the table:
- $$s_{\rm max} = 5.226\hspace{0.3cm} \Rightarrow \hspace{0.3cm} s_{\rm max}/s_{\rm eff} = \frac{5.226}{2.828} \hspace{0.15cm} \underline{\approx 1.85 \hspace{0.05cm}}.$$
In contrast, $s_{\rm max}/s_{\rm eff}= \sqrt{2} = 1.414$ would hold for both $\boldsymbol{\rm A}$ and $\boldsymbol{\rm B}$ allocations.