AWGN Channel Capacity for Continuous-Valued Input

Mutual information between continuous-value random variables

In the chapter Information-theoretical model of digital signal transmission the mutual information between the two discrete-value random variables $X$ and $Y$ was given, among other things, in the following form:

$$I(X;Y) = \hspace{-0.4cm} \sum_{(x,\hspace{0.05cm} y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ P_{XY}(x, y)}{P_{X}(x) \cdot P_{Y}(y)} \hspace{0.05cm}.$$

This equation simultaneously corresponds to the Kullback–Leibler distance between the joint probability function $P_{XY}$ and the product of the two individual probability functions $P_X$ and $P_Y$ :

$$I(X;Y) = D(P_{XY} \hspace{0.05cm} || \hspace{0.05cm}P_{X} \cdot P_{Y}) \hspace{0.05cm}.$$

In order to derive the mutual information $I(X; Y)$ between two continuous-value random variables $X$ and $Y$ , one proceeds as follows, whereby inverted commas indicate a quantised variable:

One quantises the random variables $X$ and $Y$ $($with the quantisation intervals ${\it Δ}x$ and ${\it Δ}y)$ and thus obtains the probability functions $P_{X\hspace{0.01cm}′}$ and $P_{Y\hspace{0.01cm}′}$.
The „vectors” $P_{X\hspace{0.01cm}′}$ and $P_{Y\hspace{0.01cm}′}$ become infinitely long after the boundary transitions ${\it Δ}x → 0, {\it Δ}y → 0$ , and the joint PMF $P_{X\hspace{0.01cm}′\hspace{0.08cm}Y\hspace{0.01cm}′}$ is then also infinitely extended in area.
These boundary transitions give rise to the probability density functions of the continuous random variables according to the following equations:

$$f_X(x_{\mu}) = \frac{P_{X\hspace{0.01cm}'}(x_{\mu})}{\it \Delta_x} \hspace{0.05cm}, \hspace{0.3cm}f_Y(y_{\mu}) = \frac{P_{Y\hspace{0.01cm}'}(y_{\mu})}{\it \Delta_y} \hspace{0.05cm}, \hspace{0.3cm}f_{XY}(x_{\mu}\hspace{0.05cm}, y_{\mu}) = \frac{P_{X\hspace{0.01cm}'\hspace{0.03cm}Y\hspace{0.01cm}'}(x_{\mu}\hspace{0.05cm}, y_{\mu})} {{\it \Delta_x} \cdot {\it \Delta_y}} \hspace{0.05cm}.$$

The double sum in the above equation, after renaming $Δx → {\rm d}x$ or $Δy → {\rm d}y$ , becomes the equation valid for continuous value random variables:

$$I(X;Y) = \hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ f_{XY}(x, y) } {f_{X}(x) \cdot f_{Y}(y)} \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y \hspace{0.05cm}.$$

$\text{Conclusion:}$ By splitting this double integral, it is also possible to write for the transinformation:

$$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$

The joint differential entropy

$$h(XY) = -\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big[f_{XY}(x, y) \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$

and the two differential single entropies

$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x \hspace{0.05cm},\hspace{0.5cm} h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$

On equivocation and irrelevance

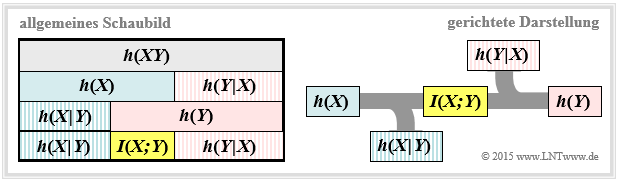
We further assume the continuous value mutual information $I(X;Y) = h(X) + h(Y) - h(XY)$ . This representation is also found in the following diagram (left graph).

Representation of the mutual information for continuous value random variables

From this you can see that the mutual information can also be represented as follows:

$$I(X;Y) = h(Y) - h(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) =h(X) - h(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}.$$

These fundamental information-theoretical relationships can also be read from the graph on the right.

This directional representation is particularly suitable for message transmission systems.

The outflowing or inflowing differential entropy characterises

the equivocation:

$$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) =\hspace{0.2cm} -\int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm},$$

the irrelevance:

$$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) =\hspace{0.2cm}- \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)} \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$

The significance of these two information-theoretic quantities will be discussed in more detail in task 4.5Z .

If one compares the graphical representations of the mutual information for

discrete value random variables in the section [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Information-theoretical_model_of_digital_signal_transmission|Information-theoretical model of digital signal transmission] continuous value random variables according to the above diagram,

the only distinguishing feature is that each „capital $H$” (entropy; larger-equal zero) has been replaced by a „non-capital $h$” (differential entropy can be positive, negative or zero) .

Otherwise, the mutual information is the same in both representations and $I(X; Y) ≥ 0$ always applies.
In the following, we mostly use the binary logarithm ⇒ $\log_2$ and thus obtain the mutual information in „bit”.

Calculation of mutual information with additive noise

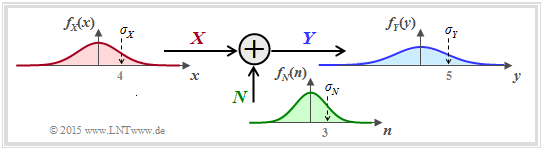
We now consider a very simple model of message transmission:

The random variable $X$ stands for the (zero mean) transmission signal and is characterised by the PDF $f_X(x)$ and the variance $σ_X^2$ . The transmission power is $P_X = σ_X^2$.
The additive noise $N$ is given by the PDF $f_N(n)$ and the noise power $P_N = σ_N^2$ .
If $X$ and $N$ are assumed to be statistically independent ⇒ signal-independent noise, then $\text{E}\big[X · N \big] = \text{E}\big[X \big] · \text{E}\big[N\big] = 0$ .
The received signal is $Y = X + N$. The output PDF $f_Y(y)$ can be calculated with the convolution operation ⇒ $f_Y(y) = f_X(x) ∗ f_N(n)$.

Message transmission system with additive noise

For the received power (variance) holds:

$$P_Y = \sigma_Y^2 = {\rm E}\big[Y^2\big] = {\rm E}\big[(X+N)^2\big] = {\rm E}\big[X^2\big] + {\rm E}\big[N^2\big] = \sigma_X^2 + \sigma_N^2 $$

$$\Rightarrow \hspace{0.3cm} P_Y = P_X + P_N \hspace{0.05cm}.$$

The sketched density functions sketched (rectangular or trapezoidal) are only intended to clarify the calculation process and have no practical relevance.
To calculate the mutual information between input $X$ and output $Y$ there are three possibilities according to the graphic on the previous subchapter drei Möglichkeiten:

Calculation according to $I(X, Y) = h(X) + h(Y) - h(XY)$:

The first two terms can be calculated in a simple way from $f_X(x)$ and $f_Y(y)$ respectively. The joint differentrial entropy $h(XY)$ is problematic. For this, one needs the 2D joint PDF $f_{XY}(x, y)$, which is usually not given directly.

Berechnung entsprechend $I(X, Y) = h(Y) - h(Y|X)$:

Hierbei bezeichnet $h(Y|X)$ die differentielle Streuentropie. Es gilt $h(Y|X) = h(X + N|X) = h(N)$, so dass $I(X; Y)$ bei Kenntnis von $f_X(x)$ und $f_N(n)$ über die Gleichung $f_Y(y) = f_X(x) ∗ f_N(n)$ sehr einfach zu berechnen ist.

Berechnung entsprechend $I(X, Y) = h(X) - h(X|Y)$:

Nach dieser Gleichung benötigt man allerdings die differentielle Rückschlussentropie $h(X|Y)$, die schwieriger angebbar ist als $h(Y|X)$.

$\text{Fazit:}$ Im Folgenden verwenden wir die mittlere Gleichung und schreiben für die Transinformation zwischen dem Eingang $X$ und dem Ausgang $Y$ eines Nachrichtenübertragungssystems bei additiver und unkorrelierter Störung $N$:

$$I(X;Y) \hspace{-0.05cm} = \hspace{-0.01cm} h(Y) \hspace{-0.01cm}- \hspace{-0.01cm}h(N) \hspace{-0.01cm}=\hspace{-0.05cm} -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.65cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y +\hspace{-0.7cm} \int\limits_{n \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_N)} \hspace{-0.65cm} f_N(n) \cdot {\rm log} \hspace{0.1cm} \big[f_N(n)\big] \hspace{0.1cm}{\rm d}n\hspace{0.05cm}.$$

Kanalkapazität des AWGN–Kanals

Spezifiziert man im bisherigen allgemeinen Systemmodell die Wahrscheinlichkeitsdichtefunktion der Störung (bzw. des Rauschens) als gaußisch entsprechend

Zur Herleitung der AWGN–Kanalkapazität

$$f_N(n) = \frac{1}{\sqrt{2\pi \sigma_N^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{n^2}/(2 \sigma_N^2) } \hspace{0.05cm}, $$

so erhalten wir das rechts skizzierte Modell zur Berechnung der Kanalkapazität des so genannten AWGN–Kanals (Additive White Gaussian Noise). Meist ersetzen wir im Folgenden $\sigma_N^2$ durch $P_N$.
Aus vorherigen Abschnitten wissen wir:

Die Kanalkapazität $C_{\rm AWGN}$ gibt die maximale Transinformation $I(X; Y)$ zwischen der Eingangsgröße $X$ und der Ausgangsgröße $Y$ des AWGN–Kanals an. Die Maximierung bezieht sich dabei auf die bestmögliche Eingangs–WDF. Somit gilt unter der Nebenbedingung der Leistungsbegrenzung:

$$C_{\rm AWGN} = \max_{f_X:\hspace{0.1cm} {\rm E}[X^2 ] \le P_X} \hspace{-0.35cm} I(X;Y) = -h(N) + \max_{f_X:\hspace{0.1cm} {\rm E}[X^2] \le P_X} \hspace{-0.35cm} h(Y) \hspace{0.05cm}.$$

Es ist bereits berücksichtigt, dass sich die Maximierung allein auf die differentielle Entropie $h(Y)$ ⇒ WDF $f_Y(y)$ bezieht. Bei gegebener Störleistung $P_N$ ist nämlich $h(N) = 1/2 · \log_2 (2π{\rm e} · P_N)$ eine Konstante.

Das Maximum für $h(Y)$ erhält man für eine Gaußsche WDF $f_Y(y)$ mit $P_Y = P_X + P_N$ t, siehe Seite Maximale differentielle Entropie bei Leistungsbegrenzung:

$${\rm max}\big[h(Y)\big] = 1/2 · \log_2 \big[2πe · (P_X + P_N)\big].$$

Die Ausgangs–WDF $f_Y(y) = f_X(x) ∗ f_N(n)$ ist aber nur dann gaußförmig, wenn sowohl $f_X(x)$ als auch $f_N(n)$ Gaußfunktionen sind. Ein plakativer Merkspruch zur Faltungsoperation lautet nämlich: Gauß bleibt Gauß, und Nicht–Gauß wird nie (exakt) Gauß.

$\text{Fazit:}$ Beim AWGN–Kanal ⇒ Gaußsche Rausch-WDF $f_N(n)$ ergibt sich die Kanalkapazität genau dann, wenn die Eingangs–WDF $f_X(x)$ ebenfalls gaußförmig ist:

Numerische Ergebnisse für die AWGN–Kanalkapazität als Funktion von ${P_X}/{P_N}$

$$C_{\rm AWGN} = h_{\rm max}(Y) - h(N) = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} {P_Y}/{P_N}$$

$$\Rightarrow \hspace{0.3cm} C_{\rm AWGN}= 1/2 \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + P_X/P_N) \hspace{0.05cm}.$$

Parallele Gaußsche Kanäle

Parallele AWGN–Kanäle

Wir betrachten nun entsprechend der Grafik $K$ parallele Gaußkanäle von $X_1 → Y_1$, ... , $X_k → Y_k$, ... , $X_K → Y_K$.

Die Sendeleistungen in den $K$ Kanälen nennen wir

$$P_1 = \text{E}[X_1^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_k = \text{E}[X_k^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_K = \text{E}[X_K^2].$$

Die $K$ Störleistungen können ebenfalls unterschiedlich sein:

$$σ_1^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_k^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_K^2.$$

Gesucht ist nun die maximale Transinformation $I(X_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, Y_K) $ zwischen

den $K$ Eingangsgrößen $X_1$, ... , $X_K$ sowie
den $K$ Ausgangsgrößen $Y_1$ , ... , $Y_K$,

die wir als die Gesamt–Kanalkapazität dieser AWGN–Konfiguration bezeichnen.

$\text{Vereinbarung:}$ Ausgegangen wird von Leistungsbegrenzung des Gesamtsystems. Das heißt:
Die Summe aller Leistungen $P_k$ in den $K$ Einzelkanälen darf den vorgegebenen Wert $P_X$ nicht überschreiten:

$$P_1 + \hspace{0.05cm}\text{...}\hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$

Unter der nur wenig einschränkenden Annahme unabhängiger Störquellen $N_1$, ... , $N_K$ kann für die Transinformation nach einigen Zwischenschritten geschrieben werden:

$$I(X_1, \hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, Y_K) = h(Y_1, ... \hspace{0.05cm}, Y_K ) - \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} h(N_k)\hspace{0.05cm}.$$

Dafür istn folgende obere Schranke angebbar:

$$I(X_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, Y_K) \hspace{0.2cm} \le \hspace{0.1cm} \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} \big[h(Y_k - h(N_k)\big] \hspace{0.2cm} \le \hspace{0.1cm} 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + {P_k}/{\sigma_k^2}) \hspace{0.05cm}.$$

Das Gleichheitszeichen (Identität) gilt bei mittelwertfreien Gaußschen Eingangsgrößen $X_k$ sowie bei statistisch voneinander unabhängigen Störungen $N_k$.
Man kommt von dieser Gleichung zur maximalen Transinformation ⇒ Kanalkapazität, wenn man die gesamte Sendeleistung $P_X$ unter Berücksichtigung der unterschiedlichen Störungen in den einzelnen Kanälen $(σ_k^2)$ bestmöglich aufteilt.
Dieses Optimierungsproblem lässt sich wieder mit dem Verfahren der Lagrange–Multiplikatoren elegant lösen. Das folgende Beispiel erläutert nur das Ergebnis.

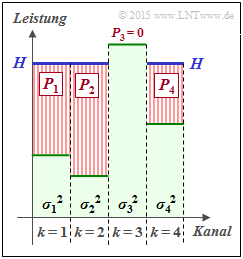
Bestmögliche Leistungsaufteilung für $K = 4$ („Water–Filling”)

$\text{Beispiel 1:}$ Wir betrachten $K = 4$ parallele Gaußkanäle mit vier unterschiedlichen Störleistungen $σ_1^2$, ... , $σ_4^2$ gemäß der nebenstehenden Abbildung (schwach–grüne Hinterlegung).

Gesucht ist die bestmögliche Aufteilung der Sendeleistung auf die vier Kanäle.
Würde man dieses Profil langsam mit Wasser auffüllen, so würde das Wasser zunächst nur in den $\text{Kanal 2}$ fließen.
Gießt man weiter, so sammelt sich auch im $\text{Kanal 1}$ etwas Wasser an und später auch im $\text{Kanal 4}$.

Die eingezeichnete „Wasserhöhe” $H$ beschreibt genau den Zeitpunkt, zu dem die Summe $P_1 + P_2 + P_4$ der insgesamt zur Verfügung stehenden Sendeleistung $P_X$ entspricht:

Die optimale Leistungsaufteilung für dieses Beispiel ergibt $P_2 > P_1 > P_4$ sowie $P_3 = 0$.
Erst bei größerer Sendeleistung $P_X$ würde auch dem dritten Kanal eine kleine Leistung $P_3$ zugewiesen.

Man bezeichnet dieses Allokationsverfahren als Water–Filling–Algorithmus.

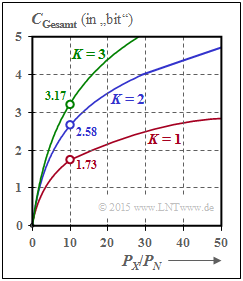
$\text{Beispiel 2:}$ Werden alle $K$ Gaußkanäle in gleicher Weise gestört ⇒ $σ_1^2 = \hspace{0.15cm}\text{...}\hspace{0.15cm} = σ_K^2 = P_N$, so sollte man natürlich die gesamte zur Verfügung stehende Sendeleistung $P_X$ gleichmäßig auf alle Kanäle verteilen: $P_k = P_X/K$. Für die Gesamtkapazität erhält man dann:

Kapazität für $K$ parallele Kanäle

$$C_{\rm Gesamt} = \frac{ K}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{K \cdot P_N}) \hspace{0.05cm}.$$

Die Grafik zeigt die Gesamtkapazität als Funktion von $P_X/P_N$ für $K = 1$, $K = 2$ und $K = 3$:

Bei $P_X/P_N = 10 \ ⇒ \ 10 · \text{lg} (P_X/P_N) = 10 \ \text{dB}$ wird die Gesamtkapazität um ca. $50\%$ größer, wenn man die Gesamtleistung $P_X$ auf zwei Kanäle gleichmäßig aufteilt: $P_1 = P_2 = P_X/2$.
Im Grenzfall $P_X/P_N → ∞$ nimmt die Gesamtkapazität um den Faktor $K$ zu ⇒ Verdoppelung bei $K = 2$.

Die beiden identischen und voneinander unabhängigen Kanäle kann man auf unterschiedliche Weise realisieren, zum Beispiel durch Multiplexverfahren in Zeit, Frequenz oder Raum.

Der Fall $K = 2$ lässt sich aber auch durch die Verwendung orthogonaler Basisfunktionen wie „Cosinus” und „Sinus” verwirklichen wie zum Beispiel bei