Differential Entropy

1 # OVERVIEW OF THE FOURTH MAIN CHAPTER #
2 Properties of continuous-value random variables
3 Entropy of continuous-value random variables after quantisation
4 Definition und Eigenschaften der differentiellen Entropie
5 Differentielle Entropie einiger spitzenwertbegrenzter Zufallsgrößen
6 Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen
7 Beweis: Maximale differentielle Entropie bei Spitzenwertbegrenzung
8 Beweis: Maximale differentielle Entropie bei Leistungsbegrenzung
9 Aufgaben zum Kapitel

# OVERVIEW OF THE FOURTH MAIN CHAPTER #

In the last chapter of this book, the information-theoretical quantities defined so far for the discrete-value case are adapted in such a way that they can also be applied to continuous-value random quantities.

For example, the entropy $H(X)$ for the discrete-value random variable $X$ becomes the differential entropy $h(X)$ in the continuous-value case..
While $H(X)$ indicates the „uncertainty” with regard to the discrete random variable $X$&nbspwith regard to the discrete random variable $h(X)$ in the same way in the continuous case.

Many of the relationships derived in the third chapter „Information between two discrete-value random variables ⇒ see table of contents for conventional entropy also apply to differential entropy. Thus, the differential joint entropy $h(XY)$ can also be given for continuous-value random variables $X$ and $Y$ and likewise the two conditional differential entropies $h(Y|X)$ and $h(X|Y)$.

In detail, this main chapter deals with:

the special features of continuous value random variables,
the definition and calculation of the differential entropy as well as its properties,
the mutual information between two value-continuous random variables,
the capacity of the AWGN channel and several such parallel Gaussian channels,
the channel coding theorem, one of the „highlights” of Shannon's information theory,
the AWGN channel capacity for discrete-value input sines (BPSK, QPSK).

Properties of continuous-value random variables

Up to now, discrete-value random variables of the form $X = \{x_1,\ x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm} , x_μ, \text{...} ,\ x_M\}$ have always been considered, which from an information-theoretical point of view are completely characterised by their probability mass function (PMF) $P_X(X)$ :

$$P_X(X) = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_{\mu},\hspace{0.05cm} \text{...}\hspace{0.15cm}, p_M \hspace{0.1cm}\big ] \hspace{0.3cm}{\rm mit} \hspace{0.3cm} p_{\mu}= P_X(x_{\mu})= {\rm Pr}( X = x_{\mu}) \hspace{0.05cm}.$$

A continuous-value random variable, ' on the other hand, can assume any value – at least in finite intervals:

Due to the uncountable supply of values, the description by a probability function is not possible in this case, or at least it does not make sense:
This would result in $M \to ∞$ as well as $p_1 \to 0$, $p_2 \to 0$, etc.

For the description of value-continuous random variables, one uses equally according to the definitions in the book Theory of Stochastic Signals :

PDF and CDF of a value-continuous random variable

the probability density function (PDF):

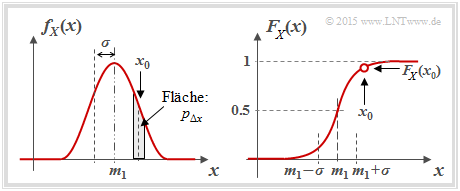
$$f_X(x_0)= \lim_{{\rm \Delta} x\to \rm 0}\frac{p_{{\rm \Delta} x}}{{\rm \Delta} x} = \lim_{{\rm \Delta} x\to \rm 0}\frac{{\rm Pr} \{ x_0- {\rm \Delta} x/\rm 2 \le \it X \le x_{\rm 0} +{\rm \Delta} x/\rm 2\}}{{\rm \Delta} x};$$

In words: the PDF value at $x_0$ gives the probability $p_{Δx}$ that $X$ lies in an (infinitely small) interval of width $Δx$ around $x_0$ , divided by $Δx$; (note the entries in the adjacent graph);

the mean value (first-order moment):

$$m_1 = {\rm E}\big[ X \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} x \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm};$$

the variance (second-order moment):

$$\sigma^2 = {\rm E}\big[(X- m_1 )^2 \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} (x- m_1 )^2 \cdot f_X(x- m_1 ) \hspace{0.1cm}{\rm d}x \hspace{0.05cm};$$

the cumulative distribution fucntion (CDF):

$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$

Note that both the PDF area and the CDF final value are always equal to $1$ .

$\text{Nomenclature notes on PDF and CDF:}$

We use in this chapter for a probability density function the representation form $f_X(x)$ often used in the literature, where holds::

$X$ denotes the (discrete-value or continuous-value) random variable,
$x$ is a possible realisation of $X$ ⇒ $x ∈ X$.

Accordingly, we denote the cumulative distribution function (CDF) of the random variable $X$ by $F_X(x)$ according to the following definition:

$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$

In other $\rm LNTwww$ books, we often write so as not to use up two characters for one variable:

For the PDF $f_x(x)$ ⇒ no distinction between random variable and realising, and
for the CDF $F_x(r) = {\rm Pr}(x ≤ r)$ ⇒ here one needs a second variable in any case.

We apologise for this formal inaccuracy.

$\text{Example 1:}$ We now consider an important special case with the uniform distribution.

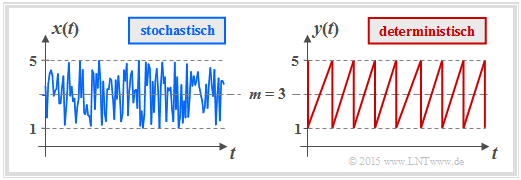
Two analogue signals as examples of continuous-value random variables

The graph shows the course of two uniformly distributed variables, which can assume all values between $1$ and $5$ $($mean value $m_1 = 3)$ with equal probability.
On the left is the result of a random process, on the right a deterministic signal with the same amplitude distribution.

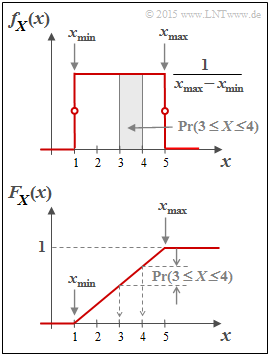
PDF and CDF of an uniformly distributed random variable

The probability density function of the uniform distribution has the course sketched in the second graph above:

$$f_X(x) = \left\{ \begin{array}{c} \hspace{0.25cm}(x_{\rm max} - x_{\rm min})^{-1} \\ 1/2 \cdot (x_{\rm max} - x_{\rm min})^{-1} \\ \hspace{0.25cm} 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ \end{array} \begin{array}{*{20}l} {x_{\rm min} < x < x_{\rm max},} \\ x ={x_{\rm min} \hspace{0.1cm}{\rm und}\hspace{0.1cm}x = x_{\rm max},} \\ x > x_{\rm max}. \\ \end{array}$$

The following equations are obtained here for the mean $m_1 ={\rm E}\big[X\big]$ and the variance $σ^2={\rm E}\big[(X – m_1)^2\big]$ :

$$m_1 = \frac{x_{\rm max} + x_{\rm min} }{2}\hspace{0.05cm}, $$

$$\sigma^2 = \frac{(x_{\rm max} - x_{\rm min})^2}{12}\hspace{0.05cm}.$$

Shown below is the cumulative distribution function (CDF):

$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$

This is identically zero for $x ≤ x_{\rm min}$, increases linearly thereafter and reaches the CDF final value of $1$ at $x = x_{\rm max}$ .
The probability that the random variable $X$ takes on a value between $3$ and $4$ can be determined from both the PDF and the CDF:

$${\rm Pr}(3 \le X \le 4) = \int_{3}^{4} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi = 0.25\hspace{0.05cm}\hspace{0.05cm},$$

$${\rm Pr}(3 \le X \le 4) = F_X(4) - F_X(3) = 0.25\hspace{0.05cm}.$$

Furthermore, note:

The result $X = 0$ is excluded for this random variable ⇒ ${\rm Pr}(X = 0) = 0$.
The result $X = 4$ , on the other hand, is quite possible. Nevertheless, auch hier ${\rm Pr}(X = 4) = 0 $also applies here.

Entropy of continuous-value random variables after quantisation

Wir betrachten nun eine wertkontinuierliche Zufallsgröße $X$ im Bereich von $0 \le x \le 1$.

Wir quantisieren die kontinuierliche Zufallsgröße $X$, um die bisherige Entropieberechnung weiter anwenden zu können. Die so entstehende diskrete (quantisierte) Größe nennen wir $Z$.
Die Quantisierungsstufenzahl sei $M$, so dass jedes Quantisierungsintervall $μ$ bei der vorliegenden WDF die Breite ${\it Δ} = 1/M$ aufweist. Die Intervallmitten bezeichnen wir mit $x_μ$.
Die Wahrscheinlichkeit $p_μ = {\rm Pr}(Z = z_μ)$ bezüglich $Z$ ist gleich der Wahrscheinlichkeit, dass die kontinuierliche Zufallsgröße $X$ einen Wert zwischen $x_μ - {\it Δ}/2$ und $x_μ + {\it Δ}/2$ besitzt.
Zunächst setzen wir $M = 2$ und verdoppeln anschließend diesen Wert in jeder Iteration. Dadurch wird die Quantisierung zunehmend feiner. Im $n$–ten Versuch gilt dann $M = 2^n$ und ${\it Δ} =2^{–n}$.

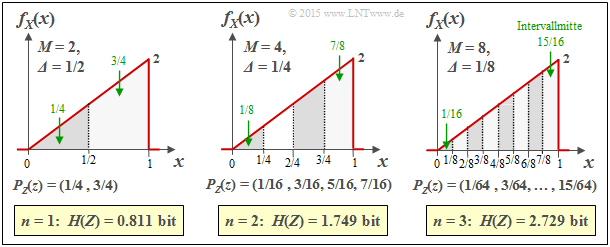
$\text{Beispiel 2:}$ Die Grafik zeigt die Ergebnisse der ersten drei Versuche für eine unsymmetrisch–dreieckförmige WDF $($zwischen $0$ und $1)$:

Entropiebestimmung der Dreieck–WDF nach Quantisierung

$n = 1 \ ⇒ \ M = 2 \ ⇒ \ {\it Δ} = 1/2\text{:}$ $H(Z) = 0.811\ \rm bit,$
$n = 2 \ ⇒ \ M = 4 \ ⇒ \ {\it Δ} = 1/4\text{:}$ $H(Z) = 1.749\ \rm bit,$
$n = 3 \ ⇒ \ M = 8 \ ⇒ \ {\it Δ} = 1/8\text{:}$ $H(Z) = 2.729\ \rm bit.$

Zudem können der Grafik noch folgende Größen entnommen werden, zum Beispiel für ${\it Δ} = 1/8$:

Die Intervallmitten liegen bei

$$x_1 = 1/16,\ x_2 = 3/16,\text{ ...} \ ,\ x_8 = 15/16 $$

$$ ⇒ \ x_μ = {\it Δ} · (μ - 1/2).$$

Die Intervallflächen ergeben sich zu

$$p_μ = {\it Δ} · f_X(x_μ) ⇒ p_8 = 1/8 · (7/8+1)/2 = 15/64.$$

Damit erhält man für die Wahrscheinlichkeitsfunktion der quantisierten Zufallsgröße $Z$:

$$P_Z(Z) = (1/64, \ 3/64, \ 5/64, \ 7/64, \ 9/64, \ 11/64, \ 13/64, \ 15/64).$$

$\text{Fazit:}$ Die Ergebnisse dieses Experiments interpretieren wir wie folgt:

Die Entropie $H(Z)$ wird mit steigendem $M$ immer größer.
Der Grenzwert von $H(Z)$ für $M \to ∞ \ ⇒ \ {\it Δ} → 0$ ist unendlich.
Damit ist auch die Entropie $H(X)$ der wertkontinuierlichen Zufallsgröße $X$ unendlich groß.
Daraus folgt: Die bisherige Entropie–Definition versagt hier.

Zur Verifizierung unseres empirischen Ergebnisses gehen wir von folgender Gleichung aus:

$$H(Z) = \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} p_{\mu} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\mu}}= \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} {\it \Delta} \cdot f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{{\it \Delta} \cdot f_X(x_{\mu} )}\hspace{0.05cm}.$$

Wir spalten nun $H(Z) = S_1 + S_2$ in zwei Summen auf:

$$\begin{align*}S_1 & = {\rm log}_2 \hspace{0.1cm} \frac{1}{\it \Delta} \cdot \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.02cm} {\it \Delta} \cdot f_X(x_{\mu} ) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.05cm},\\ S_2 & = \hspace{0.05cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x_{\mu} ) } \cdot {\it \Delta} \hspace{0.2cm}\approx \hspace{0.2cm} \int_{0}^{1} \hspace{0.05cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$

Die Näherung $S_1 ≈ -\log_2 {\it Δ}$ gilt exakt nur im Grenzfall ${\it Δ} → 0$.
Die angegebene Näherung für $S_2$ gilt ebenfalls nur für kleine ${\it Δ} → {\rm d}x$, so dass man die Summe durch das Integral ersetzen sollte.

$\text{Verallgemeinerung:}$ Nähert man die wertkontinuierliche Zufallsgröße $X$ mit der WDF $f_X(x)$ durch eine wertdiskrete Zufallsgröße $Z$ an, indem man eine (feine) Quantisierung mit der Intervallbreite ${\it Δ}$ durchführt, so erhält man für die Entropie der Zufallsgröße $Z$:

$$H(Z) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm}+ \hspace{-0.35cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x = - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm} + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$

Das Integral beschreibt die differentielle Entropie $h(X)$ der wertkontinuierlichen Zufallsgröße $X$. Für den Sonderfall ${\it Δ} = 1/M = 2^{-n}$ kann die obige Gleichung auch wie folgt geschrieben werden:

$$H(Z) = n + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$

Im Grenzfall ${\it Δ} → 0 \ ⇒ \ M → ∞ \ ⇒ \ n → ∞$ ist auch die Entropie der wertkontinuierlichen Zufallsgröße unendlich groß: $H(X) → ∞$.
Auch bei kleinerem $n$ stellt diese Gleichung lediglich eine Näherung für $H(Z)$ dar, wobei die differentielle Entropie $h(X)$ der wertkontinuierlichen Größe als Korrekturfaktor dient.

$\text{Beispiel 3:}$ Wir betrachten wie im $\text{Beispiel 2}$ eine Dreieck–WDF $($zwischen $0$ und $1)$. Deren differentielle Entropie ergibt sich, wie in Aufgabe 4.2 berechnet, zu

Entropie der Dreieck–WDF nach Quantisierung

$$h(X) = \hspace{0.05cm}-0.279 \ \rm bit.$$

In der Tabelle ist die Entropie $H(Z)$ der mit $n$ Bit quantisierten Größe $Z$ angegeben.

Man erkennt schon für $n = 3$ eine gute Übereinstimmung zwischen Näherung (untere Zeile) und der exakten Berechnung (Zeile 2).

Für $n = 10$ wird die Näherung noch besser mit der exakten Berechnung (die extrem aufwändig ist) übereinstimmen.

Definition und Eigenschaften der differentiellen Entropie

$\text{Verallgemeinerung:}$ Die differentielle Entropie $h(X)$ einer wertkontinuierlichen Zufallsgröße $X$ lautet mit der Wahrscheinlichkeitsdichtefunktion $f_X(x)$:

$$h(X) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[ f_X(x) \big] \hspace{0.1cm}{\rm d}x \hspace{0.6cm}{\rm mit}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} \hspace{0.05cm}.$$

Hinzugefügt werden muss jeweils eine Pseudo–Einheit:

„nat” bei Verwendung von „ln” ⇒ natürlicher Logarithmus,
„bit” bei Verwendung von „log₂” ⇒ Logarithmus dualis.

Während für die (herkömmliche) Entropie einer wertdiskreten Zufallsgröße $X$ stets $H(X) ≥ 0$ gilt, kann die differentielle Entropie $h(X)$ einer wertkontinuierlichen Zufallsgröße auch negativ sein. Daraus ist bereits ersichtlich, dass $h(X)$ im Gegensatz zu $H(X)$ nicht als „Unsicherheit” interpretiert werden kann.

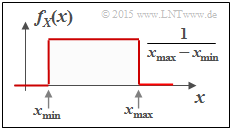
WDF einer gleichverteilten Zufallsgröße

$\text{Beispiel 4:}$ Die obere Grafik zeigt die Wahrscheinlichkeitsdichte einer zwischen $x_{\rm min}$ und $x_{\rm max}$ gleichverteilten Zufallsgröße $X$. Für deren differentielle Entropie erhält man in „nat”:

$$\begin{align*}h(X) & = - \hspace{-0.18cm}\int\limits_{x_{\rm min} }^{x_{\rm max} } \hspace{-0.28cm} \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \cdot {\rm ln} \hspace{0.1cm}\big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \hspace{0.1cm}{\rm d}x \\ & = {\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \cdot \big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big ]_{x_{\rm min} }^{x_{\rm max} }={\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big]\hspace{0.05cm}.\end{align*} $$

Die Gleichung für die differentielle Entropie in „bit” lautet:

$$h(X) = \log_2 \big[x_{\rm max} – x_{ \rm min} \big].$$

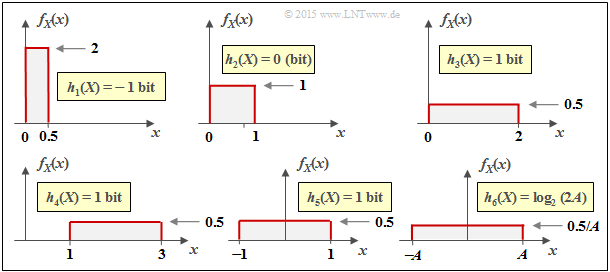
$h(X)$ für verschiedene rechteckförmige Dichtefunktionen

Die linke Grafik zeigt anhand einiger Beispiele die numerische Auswertung des obigen Ergebnisses.

$\text{Interpretation:}$ Aus den sechs Skizzen im letzten Beispiel lassen sich wichtige Eigenschaften der differentiellen Entropie $h(X)$ ablesen:

Die differentielle Entropie wird durch eine WDF–Verschiebung $($um $k)$ nicht verändert:

$$h(X + k) = h(X) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \text{Beispielsweise gilt} \ \ h_3(X) = h_4(X) = h_5(X) \hspace{0.05cm}.$$

$h(X)$ ändert sich durch Stauchung/Spreizung der WDF um den Faktor $k ≠ 0$ wie folgt:

$$h( k\hspace{-0.05cm} \cdot \hspace{-0.05cm}X) = h(X) + {\rm log}_2 \hspace{0.05cm} \vert k \vert \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \text{Beispielsweise gilt} \ \ h_6(X) = h_5(AX) = h_5(X) + {\rm log}_2 \hspace{0.05cm} (A) = {\rm log}_2 \hspace{0.05cm} (2A) \hspace{0.05cm}.$$

Des Weiteren gelten viele der im Kapitel Verschiedene Entropien zweidimensionaler Zufallsgrößen für den wertdiskreten Fall hergeleitete Gleichungen auch für wertkontinuierliche Zufallsgrößen.

Aus der folgenden Zusammenstellung erkennt man, dass oft nur das (große) $H$ durch ein (kleines) $h$ sowie die Wahrscheinlichkeitsfunktion (englische Abkürzung: $\rm PMF)$ durch die entsprechende Wahrscheinlichkeitsdichtefunktion $\rm (PDF$ bzw. $\rm WDF)$ zu ersetzen ist.

Bedingte differentielle Entropie (englisch: Conditional Differential Entropy):

$$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm}h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.04cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$

Differentielle Verbundentropie (englisch: Joint Differential Entropy):

$$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ P_{XY}(x, y)} \hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm}h(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{f_{XY}(X, Y)}\right ] =\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.04cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_{XY}(x, y) } \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$

Kettenregel der differentiellen Entropie:

$$H(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} H(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) \le \sum_{i = 1}^{n} H(X_i) \hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm} h(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} h(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) \le \sum_{i = 1}^{n} h(X_i) \hspace{0.05cm}.$$

Kullback–Leibler–Distanz zwischen den Zufallsgrößen $X$ und $Y$:

$$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{X})\hspace{-0.8cm}} P_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{P_X(x)}{P_Y(x)} \ge 0$$

$$\Rightarrow \hspace{0.3cm}D(f_X \hspace{0.05cm} || \hspace{0.05cm}f_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{f_X(X)}{f_Y(X)}\right ] \hspace{0.2cm}= \hspace{-0.4cm}\int\limits_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{f_X(x)}{f_Y(x)} \hspace{0.15cm}{\rm d}x \ge 0 \hspace{0.05cm}.$$

Differentielle Entropie einiger spitzenwertbegrenzter Zufallsgrößen

Differentielle Entropie spitzenwertbegrenzter Zufallsgrößen

Die Tabelle zeigt die Ergebnisse hinsichtlich der differentiellen Entropie für drei beispielhafte Wahrscheinlichkeitsdichtefunktionen $f_X(x)$. Diese sind alle spitzenwertbegrenzt, das heißt, es gilt jeweils $|X| ≤ A$.

Bei Spitzenwertbegrenzung kann man die differentielle Entropie stets wie folgt darstellen:

$$h(X) = {\rm log}\,\, ({\it \Gamma}_{\rm A} \cdot A).$$

Das Argument ${\it \Gamma}_A · A$ ist unabhängig davon, welchen Logarithmus man verwendet. Anzufügen ist

bei Verwendung von $\ln$ die Pseudo–Einheit „nat”,
bei Verwendung von $\log_2$ die Pseudo–Einheit „bit”.

$\text{Theorem:}$ Unter der Nebenbedingung Spitzenwertbegrenzung (englisch: Peak Constraint) ⇒ also WDF $f_X(x) = 0$ für $ \vert x \vert > A$ – führt die Gleichverteilung zur maximalen differentiellen Entropie:

$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} (2A)\hspace{0.05cm}.$$

Hier ist die geeignete Kenngröße ${\it \Gamma}_{\rm A} = 2$ maximal. Sie finden den Beweis am Ende dieses Kapitels.

Das Theorem bedeutet gleichzeitig, dass bei jeder anderen spitzenwertbegrenzten WDF (außer der Gleichverteilung) der Kennparameter ${\it \Gamma}_{\rm A} < 2$ ist.

Für die symmetrische Dreieckverteilung ergibt sich nach obiger Tabelle ${\it \Gamma}_{\rm A} = \sqrt{\rm e} ≈ 1.649$.
Beim einseitigen Dreieck $($zwischen $0$ und $A)$ ist demgegenüber ${\it \Gamma}_{\rm A}$ nur halb so groß.
Auch für jedes andere Dreieck $($Breite $A$, Spitze beliebig zwischen $0$ und $A)$ gilt ${\it \Gamma}_{\rm A} ≈ 0.824$.

Die jeweils zweite $h(X)$–Angabe und die Kenngröße ${\it \Gamma}_{\rm L}$ eignet sich dagegen für den Vergleich von Zufallsgrößen bei Leistungsbegrenzung, der im nächsten Abschnitt behandelt wird. Unter dieser Nebenbedingung ist zum Beispiel die symmetrische Dreieckverteilung $({\it \Gamma}_{\rm L} ≈ 16.31)$ besser als die Gleichverteilung ${\it \Gamma}_{\rm L} = 12)$.

Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen

Die differentiellen Entropien $h(X)$ für drei beispielhafte Dichtefunktionen $f_X(x)$ ohne Begrenzung, die durch entsprechende Parameterwahl alle die gleiche Varianz $σ^2 = {\rm E}\big[|X -m_x|^2 \big]$ und damit gleiche Streuung $σ$ aufweisen, sind der folgenden Tabelle zu entnehmen. Berücksichtigt sind:

Differentielle Entropie leistungsbegrenzter Zufallsgrößen

die Gaußverteilung,
die Laplaceverteilung ⇒ eine zweiseitige Exponentialverteilung,
die (einseitige) Exponentialverteilung.

Die differentielle Entropie lässt sich hier stets darstellen als

$$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm L} \cdot \sigma^2).$$

Das Ergebnis unterscheidet sich nur durch die Pseudo–Einheit

„nat” bei Verwendung von $\ln$ bzw.
„bit” bei Verwendung vo n $\log_2$.

$\text{Theorem:}$ Unter der Nebenbedingung der Leistungsbegrenzung (englisch: Power Constraint) führt die Gaußverteilung

$$f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2} } \cdot {\rm exp} \left [ - \hspace{0.05cm}\frac{(x - m_1)^2}{2 \sigma^2}\right ]$$

unabhängig vom Mittelwert $m_1$ zur maximalen differentiellen Entropie:

$$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08\hspace{0.05cm}.$$

Sie finden den Beweis am Ende dieses Kapitels.

Diese Aussage bedeutet gleichzeitig, dass für jede andere WDF als die Gaußverteilung die Kenngröße ${\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08$ sein wird. Beispielsweise ergibt sich der Kennwert

für die Dreieckverteilung zu ${\it \Gamma}_{\rm L} = 6{\rm e} ≈ 16.31$,
für die Laplaceverteilung zu ${\it \Gamma}_{\rm L} = 2{\rm e}^2 ≈ 14.78$, und
für die Gleichverteilung zu $Γ_{\rm L} = 12$ .

Beweis: Maximale differentielle Entropie bei Spitzenwertbegrenzung

Unter der Nebenbedingung der Spitzenwertbegrenzung ⇒ $|X| ≤ A$ gilt für die differentielle Entropie:

$$h(X) = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Von allen möglichen Wahrscheinlichkeitsdichtefunktionen $f_X(x)$, die die Bedingung

$$\int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x = 1$$

erfüllen, ist nun diejenige Funktion $g_X(x)$ gesucht, die zur maximalen differentiellen Entropie $h(X)$ führt.

Zur Herleitung benutzen wir das Verfahren der Lagrange–Multiplikatoren:

Wir definieren die Lagrange–Kenngröße $L$ in der Weise, dass darin sowohl $h(X)$ als auch die Nebenbedingung $|X| ≤ A$ enthalten sind:

$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.5cm}+ \hspace{0.5cm} \lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Wir setzen allgemein $f_X(x) = g_X(x) + ε · ε_X(x)$, wobei $ε_X(x)$ eine beliebige Funktion darstellt, mit der Einschränkung, dass die WDF–Fläche gleich $1$ sein muss. Damit erhalten wir:

$$\begin{align*}L = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm}\big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x)\big ] \cdot {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) + \varepsilon \cdot \varepsilon_X(x) } \hspace{0.1cm}{\rm d}x + \lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} \big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x) \big ] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$

Die bestmögliche Funktion ergibt sich dann, wenn es für $ε = 0$ eine stationäre Lösung gibt:

$$\left [\frac{{\rm d}L}{{\rm d}\varepsilon} \right ]_{\varepsilon \hspace{0.05cm}= \hspace{0.05cm}0}=\hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \cdot \big [ {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 \big ]\hspace{0.1cm}{\rm d}x \hspace{0.3cm} + \hspace{0.3cm}\lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \hspace{0.1cm}{\rm d}x \stackrel{!}{=} 0 \hspace{0.05cm}.$$

Diese Bedingungsgleichung ist unabhängig von $ε_X$ nur dann zu erfüllen, wenn gilt:

$${\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 + \lambda = 0 \hspace{0.4cm} \forall x \in \big[-A, +A \big]\hspace{0.3cm} \Rightarrow\hspace{0.3cm} g_X(x) = {\rm const.}\hspace{0.4cm} \forall x \in \big [-A, +A \big]\hspace{0.05cm}.$$

$\text{Resümee bei Spitzenwertbegrenzung:}$

Die maximale differentielle Entropie ergibt sich unter der Nebenbedingung $ \vert X \vert ≤ A$ für die Gleichverteilung (englisch: Uniform PDF):

$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm A} \cdot A) = {\rm log} \hspace{0.1cm} (2A) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm A} = 2 \hspace{0.05cm}.$$

Jede andere Zufallsgröße mit der WDF–Eigenschaft $f_X(\vert x \vert > A) = 0$ führt zu einer kleineren differentiellen Entropie, gekennzeichnet durch den Parameter ${\it \Gamma}_{\rm A} < 2$.

Beweis: Maximale differentielle Entropie bei Leistungsbegrenzung

Vorneweg zur Begriffserklärung:

Eigentlich wird nicht die Leistung ⇒ das zweite Moment $m_2$ begrenzt, sondern das zweite Zentralmoment ⇒ Varianz $μ_2 = σ^2$.
Gesucht wird also nun die maximale differentielle Entropie unter der Nebenbedingung ${\rm E}\big[|X – m_1|^2 \big] ≤ σ^2$.
Das $≤$–Zeichen dürfen wir hierbei durch das Gleichheitszeichen ersetzen.

Lassen wir nur mittelwertfreie Zufallsgrößen zu, so umgehen wir das Problem. Damit lautet der Lagrange-Multiplikator:

$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} \lambda_1 \cdot \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} \lambda_2 \cdot \int_{-\infty}^{+\infty}\hspace{-0.1cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Nach ähnlichem Vorgehen wie beim Beweis für Spitzenwertbegrenzung zeigt sich, dass die „bestmögliche” Funktion $g_X(x) \sim {\rm e}^{–λ_2\hspace{0.05cm} · \hspace{0.05cm} x^2}$ sein muss ⇒ Gaußverteilung:

$$g_X(x) ={1}/{\sqrt{2\pi \sigma^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{x^2}/{(2 \sigma^2)} }\hspace{0.05cm}.$$

Wir verwenden hier aber für den expliziten Beweis die Kullback–Leibler–Distanz zwischen einer geeigneten allgemeinen WDF $f_X(x)$ und der Gauß–WDF $g_X(x)$:

$$D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = \int_{-\infty}^{+\infty} \hspace{0.02cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} \frac{f_X(x)}{g_X(x)} \hspace{0.1cm}{\rm d}x = -h(X) - I_2\hspace{0.3cm} \Rightarrow\hspace{0.3cm}I_2 = \int_{-\infty}^{+\infty} \hspace{0.02cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} {g_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Zur Vereinfachung ist hier der natürliche Logarithmus ⇒ $\ln$ verwendet. Damit erhalten wir für das zweite Integral:

$$I_2 = - \frac{1}{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{-0.4cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.3cm}- \hspace{0.3cm} \frac{1}{2\sigma^2} \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{0.02cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Das erste Integral ist definitionsgemäß gleich $1$ und das zweite Integral ergibt $σ^2$:

$$I_2 = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) - {1}/{2} \cdot [{\rm ln} \hspace{0.1cm} ({\rm e})] = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)$$

$$\Rightarrow\hspace{0.3cm} D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = -h(X) - I_2 = -h(X) + {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$

Da auch bei wertkontinuierlichen Zufallsgrößen die Kullback–Leibler–Distanz stets $\ge 0$ ist, erhält man nach Verallgemeinerung („ln” ⇒ „log”):

$$h(X) \le {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$

Das Gleichzeichen gilt nur, wenn die Zufallsgröße $X$ gaußverteilt ist.

$\text{Resümee bei Leistungsbegrenzung:}$

Die maximale differentielle Entropie ergibt sich unter der Bedingung ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ unabhängig von $m_1$ für die Gaußverteilung (englisch: Gaussian PDF):

$$h_{\rm max}(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm} \rm L} \cdot \sigma^2) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm L} = 2\pi{\rm e} \hspace{0.05cm}.$$

Jede andere wertkontinuierliche Zufallsgröße $X$ mit Varianz ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ führt zu einem kleineren Wert, gekennzeichnet durch die Kenngröße ${\it \Gamma}_{\rm L} < 2πe$.