Difference between revisions of "Mobile Communications/General Description of Time Variant Systems"
| Line 9: | Line 9: | ||
<br> | <br> | ||
| − | Nach der Zeitvarianz wird nun der Begriff der ''Frequenzselektivität'' eingeführt und an Beispielen verdeutlicht, eine Kanaleigenschaft, die für die mobile Kommunikation ebenfalls von großer Bedeutung ist. Wie im gesamten Buch erfolgt die Beschreibung im äquivalenten Tiefpassbereich. | + | Nach der Zeitvarianz wird nun der Begriff der ''Frequenzselektivität'' eingeführt und an Beispielen verdeutlicht, eine Kanaleigenschaft, die für die mobile Kommunikation ebenfalls von großer Bedeutung ist. Wie im gesamten Buch erfolgt die Beschreibung im äquivalenten Tiefpassbereich. |
Im Einzelnen werden behandelt: | Im Einzelnen werden behandelt: | ||
| Line 20: | Line 20: | ||
| − | Weitere Informationen zum Thema sowie Aufgaben | + | Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im Versuch „Mobilfunkkanal” des Praktikums „Simulation digitaler Übertragungssysteme”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf |
| − | *dem [http://en.lntwww.de/downloads/Sonstiges/Programme/MFK.zip Windows–Programm MFK] ⇒ Link verweist auf die ZIP-Version des Programms und | + | *dem [http://en.lntwww.de/downloads/Sonstiges/Programme/MFK.zip Windows–Programm MFK] ⇒ Link verweist auf die ZIP-Version des Programms und |
| − | *der zugehörigen [http://en.lntwww.de/downloads/Sonstiges/Texte/Mobilfunkkanal.pdf Praktikumsanleitung] ⇒ Link verweist auf die PDF-Version (58 Seiten). | + | *der zugehörigen [http://en.lntwww.de/downloads/Sonstiges/Texte/Mobilfunkkanal.pdf Praktikumsanleitung] ⇒ Link verweist auf die PDF-Version (58 Seiten). |
| Line 28: | Line 28: | ||
== Übertragungsfunktion und Impulsantwort == | == Übertragungsfunktion und Impulsantwort == | ||
<br> | <br> | ||
| − | Die Beschreibungsgrößen eines Nachrichtenübertragungssystems wurden bereits in den Kapiteln [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Frequenzbereich|Systembeschreibung im Frequenzbereich]] bzw. [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich|Systembeschreibung im Zeitbereich]] des Buches „Lineare zeitvariante Systeme” eingeführt und eingehend diskutiert. Die wichtigsten Ergebnisse sollen hier nochmals kurz zusammengefasst werden.<br> | + | Die Beschreibungsgrößen eines Nachrichtenübertragungssystems wurden bereits in den Kapiteln [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Frequenzbereich|Systembeschreibung im Frequenzbereich]] bzw. [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich|Systembeschreibung im Zeitbereich]] des Buches „Lineare zeitvariante Systeme” eingeführt und eingehend diskutiert. Die wichtigsten Ergebnisse sollen hier nochmals kurz zusammengefasst werden.<br> |
[[File:Mob_T_2_1_S1_neu.png|right|frame|Betrachtetes LZI–System|class=fit]] | [[File:Mob_T_2_1_S1_neu.png|right|frame|Betrachtetes LZI–System|class=fit]] | ||
| − | Vorausgesetzt wird zunächst ein ''lineares und zeitinvariantes System'' ⇒ '''LZI–System''' mit dem Signal $s(t)$ am Eingang und dem Ausgangssignal $r(t)$. Der Einfachheit halber seien $s(t)$ und $r(t)$ reell. Dann gilt: | + | Vorausgesetzt wird zunächst ein ''lineares und zeitinvariantes System'' ⇒ '''LZI–System''' mit dem Signal $s(t)$ am Eingang und dem Ausgangssignal $r(t)$. Der Einfachheit halber seien $s(t)$ und $r(t)$ reell. Dann gilt: |
| − | *Das System lässt sich vollständig durch die [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang|Übertragungsfunktion]] $H(f)$ charakterisieren. Man bezeichnet $H(f)$ auch als den <i>Frequenzgang</i>. Definitionsgemäß gilt $H(f) = R(f)/S(f)$.<br> | + | *Das System lässt sich vollständig durch die [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang|Übertragungsfunktion]] $H(f)$ charakterisieren. Man bezeichnet $H(f)$ auch als den <i>Frequenzgang</i>. Definitionsgemäß gilt $H(f) = R(f)/S(f)$.<br> |
| − | *Ebenso ist das System durch die [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich#Impulsantwort|Impulsantwort]] $h(t)$ als die [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_zweite_Fourierintegral|Fourierrücktransformierte]] von $H(f)$ vollständig gekennzeichnet. Das Ausgangssignal ergibt sich aus der Faltung: | + | *Ebenso ist das System durch die [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich#Impulsantwort|Impulsantwort]] $h(t)$ als die [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_zweite_Fourierintegral|Fourierrücktransformierte]] von $H(f)$ vollständig gekennzeichnet. Das Ausgangssignal ergibt sich aus der Faltung: |
::<math>r(t) = s(t) \star h(t) \hspace{0.4cm} {\rm mit} \hspace{0.4cm} h(t) | ::<math>r(t) = s(t) \star h(t) \hspace{0.4cm} {\rm mit} \hspace{0.4cm} h(t) | ||
| Line 40: | Line 40: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Um die durch $H(f)$ bzw. $h(t)$ entstehenden linearen Verzerrungen zu erkennen, eignen sich die folgenden Eingangssignale: | + | Um die durch $H(f)$ bzw. $h(t)$ entstehenden linearen Verzerrungen zu erkennen, eignen sich die folgenden Eingangssignale: |
| − | *ein [[Signaldarstellung/Einige_Sonderf%C3%A4lle_impulsartiger_Signale#Diracimpuls|Diracimpuls]]: $s(t) = \delta(t)$ ⇒ $r(t) = h(t)$ ⇒ <i>Impulsantwort</i>,<br> | + | *ein [[Signaldarstellung/Einige_Sonderf%C3%A4lle_impulsartiger_Signale#Diracimpuls|Diracimpuls]]: $s(t) = \delta(t)$ ⇒ $r(t) = h(t)$ ⇒ <i>Impulsantwort</i>,<br> |
| − | *eine [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich#Sprungantwort|Sprungfunktion]]: $s(t) = \gamma(t)$ ⇒ $r(t) = \gamma(t) \star h(t)$ ⇒ <i>Sprungantwort</i>,<br> | + | *eine [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich#Sprungantwort|Sprungfunktion]]: $s(t) = \gamma(t)$ ⇒ $r(t) = \gamma(t) \star h(t)$ ⇒ <i>Sprungantwort</i>,<br> |
| − | *ein [[Signaldarstellung/Zeitdiskrete_Signaldarstellung#Diracpuls_im_Zeit-_und_im_Frequenzbereich|Diracpuls]]: $s(t) = p_\delta(t)$ ⇒ $r(t) = p_\delta(t) \star h(t)$ ⇒ <i>Pulsantwort</i>.<br> | + | *ein [[Signaldarstellung/Zeitdiskrete_Signaldarstellung#Diracpuls_im_Zeit-_und_im_Frequenzbereich|Diracpuls]]: $s(t) = p_\delta(t)$ ⇒ $r(t) = p_\delta(t) \star h(t)$ ⇒ <i>Pulsantwort</i>.<br> |
| − | Dagegen ist ein Gleichsignal $s(t) = A$ nicht geeignet, die Frequenzabhängigkeit des LZI–Systems sichtbar werden zu lassen. Bei einem Tiefpass–System wäre dann das Ausgangssignal unabhängig von $H(f)$ stets konstant: $r(t) = A \cdot H(f= 0)$.<br> | + | Dagegen ist ein Gleichsignal $s(t) = A$ nicht geeignet, die Frequenzabhängigkeit des LZI–Systems sichtbar werden zu lassen. Bei einem Tiefpass–System wäre dann das Ausgangssignal unabhängig von $H(f)$ stets konstant: $r(t) = A \cdot H(f= 0)$.<br> |
| − | Auf der nächsten Seite betrachten wir als Eingangssignal $s(t)$ einen Diracpuls $p_\delta(t)$. Hiermit lassen sich die Gemeinsamkeiten und Unterschiede zwischen zeitinvarianten und zeitvarianten Systemen sehr anschaulich darstellen.<br> | + | Auf der nächsten Seite betrachten wir als Eingangssignal $s(t)$ einen Diracpuls $p_\delta(t)$. Hiermit lassen sich die Gemeinsamkeiten und Unterschiede zwischen zeitinvarianten und zeitvarianten Systemen sehr anschaulich darstellen.<br> |
| − | <i>Hinweis:</i> Die Eigenschaften von $H(f)$ und $h(t)$ werden im Lernvideo [[Einige_Anmerkungen_zur_Übertragungsfunktion_(Lernvideo)|Einige Anmerkungen zur Übertragungsfunktion]] ausführlich behandelt.<br> | + | <i>Hinweis:</i> Die Eigenschaften von $H(f)$ und $h(t)$ werden im Lernvideo [[Einige_Anmerkungen_zur_Übertragungsfunktion_(Lernvideo)|Einige Anmerkungen zur Übertragungsfunktion]] ausführlich behandelt.<br> |
| Line 57: | Line 57: | ||
Die Grafik soll den Unterschied zwischen einem zeitinvarianten Kanal („'''LZI'''”) und einem zeitvarianten Kanal („'''LZV'''”) verdeutlichen.<br> | Die Grafik soll den Unterschied zwischen einem zeitinvarianten Kanal („'''LZI'''”) und einem zeitvarianten Kanal („'''LZV'''”) verdeutlichen.<br> | ||
| − | [[File:P ID2142 Mob T 2 1 S2 v1.png| | + | [[File:P ID2142 Mob T 2 1 S2 v1.png|right|frame|Zeitinvarianter und zeitvarianter Kanal|class=fit]] |
Man erkennt aus dieser Darstellung: | Man erkennt aus dieser Darstellung: | ||
| − | *Das Sendesignal $s(t)$ ist hier ein Diracpuls $p_\delta(t)$, also eine unendliche Folge von Diracimpulsen in äquidistanten Abständen $T$, alle mit dem Gewicht $1$ (siehe obere Grafik): | + | *Das Sendesignal $s(t)$ ist hier ein Diracpuls $p_\delta(t)$, also eine unendliche Folge von Diracimpulsen in äquidistanten Abständen $T$, alle mit dem Gewicht $1$ (siehe obere Grafik): |
::<math>s(t) = p_{\rm \delta} (t) = \sum_{n = -\infty}^{+\infty} {\rm \delta} (t - n \cdot T) | ::<math>s(t) = p_{\rm \delta} (t) = \sum_{n = -\infty}^{+\infty} {\rm \delta} (t - n \cdot T) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Grün markiert ist der Diracimpuls bei $t = 0$. Mit $s(t) = {\rm \delta}(t)$ ist das Signal am Kanalausgang gleich $r(t) = h(t)$ entsprechend der grünen Hinterlegung. Vorausgesetzt wird zunächst, dass die Ausdehnung der Impulsantwort $h(t)$ | + | *Grün markiert ist der Diracimpuls bei $t = 0$. Mit $s(t) = {\rm \delta}(t)$ ist das Signal am Kanalausgang gleich $r(t) = h(t)$ entsprechend der grünen Hinterlegung. Vorausgesetzt wird zunächst, dass die Ausdehnung der Impulsantwort $h(t)$ kleiner ist als $T$.<br> |
| − | *Für das gesamte Empfangssignal nach dem LZI–Kanal | + | *Für das gesamte Empfangssignal nach dem LZI–Kanal gemäß der mittleren Grafik kann dann geschrieben werden: |
::<math>r(t) = p_{\rm \delta} (t) \star h(t) = \sum_{n = -\infty}^{+\infty} h (t - n \cdot T) | ::<math>r(t) = p_{\rm \delta} (t) \star h(t) = \sum_{n = -\infty}^{+\infty} h (t - n \cdot T) | ||
| Line 76: | Line 76: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Fazit:}$ Bei einem zeitvarianten Kanal kann man keine einparametrige Impulsantwort $h(t)$ und | + | $\text{Fazit:}$ Bei einem '''zeitvarianten Kanal''' kann man keine einparametrige Impulsantwort $h(t)$ und somit auch keine Übertragungsfunktion $H(f)$ angeben.}}<br> |
| − | <i>Hinweis:</i> Das Lernvideo [[Eigenschaften_des_Übertragungskanals_(Lernvideo)|Eigenschaften des Übertragungskanals]] beschreibt die Unterschiede zwischen LZV– und LZI–Systemen.<br> | + | <i>Hinweis:</i> Das Lernvideo [[Eigenschaften_des_Übertragungskanals_(Lernvideo)|Eigenschaften des Übertragungskanals]] beschreibt die Unterschiede zwischen LZV– und LZI–Systemen.<br> |
== Zweidimensionale Impulsantwort == | == Zweidimensionale Impulsantwort == | ||
| Line 85: | Line 85: | ||
[[File:P ID2143 Mob T 2 1 S3 v1.png|right|frame|Zweidimensionale Impulsantwort|class=fit]] | [[File:P ID2143 Mob T 2 1 S3 v1.png|right|frame|Zweidimensionale Impulsantwort|class=fit]] | ||
| − | Voraussetzung hierfür ist, dass der Kanal weiterhin linear ist; man spricht dann von einem '''LZV–System''' (linear zeitvariant). | + | Voraussetzung hierfür ist, dass der Kanal weiterhin linear ist; man spricht dann von einem '''LZV–System''' (linear zeitvariant). |
Es gelten folgende Zusammenhänge: | Es gelten folgende Zusammenhänge: | ||
| Line 93: | Line 93: | ||
<br clear=all> | <br clear=all> | ||
Zur letzten Gleichung und obiger Grafik ist anzumerken: | Zur letzten Gleichung und obiger Grafik ist anzumerken: | ||
| − | *Der Parameter $\tau$ gibt die '''Verzögerungszeit''' zur Kennzeichnung der Zeitdispersion an. Durch Ausschreiben der Faltungsoperation ist es gelungen, dass $\tau$ auch der Parameter der LZI–Impulsantwort ist. Auf den letzten Seiten wurde noch von $h(t)$ gesprochen.<br> | + | *Der Parameter $\tau$ gibt die '''Verzögerungszeit''' zur Kennzeichnung der Zeitdispersion an. Durch Ausschreiben der Faltungsoperation ist es gelungen, dass $\tau$ auch der Parameter der LZI–Impulsantwort ist. Auf den letzten Seiten wurde noch von $h(t)$ gesprochen.<br> |
| − | *Der zweite Parameter der Impulsantwort bzw. die zweite Achse kennzeichnet die '''absolute Zeit''' $t$, die unter anderem zur Beschreibung der Zeitvarianz herangezogen wird. Zu unterschiedlichen Zeiten $t$ hat die Impulsantwort $h(\tau, \hspace{0.05cm}t)$ eine andere Form.<br> | + | *Der zweite Parameter der Impulsantwort bzw. die zweite Achse kennzeichnet die '''absolute Zeit''' $t$, die unter anderem zur Beschreibung der Zeitvarianz herangezogen wird. Zu unterschiedlichen Zeiten $t$ hat die Impulsantwort $h(\tau, \hspace{0.05cm}t)$ eine andere Form.<br> |
| − | *Eine Besonderheit der 2D–Darstellung ist, dass die $t$–Achse zeitdiskret (bei Vielfachen von $T$) aufgetragen wird, während die $\tau$–Achse wie im gezeigten Beispiel zeitkontinuierlich sein kann. Im Mobilfunk wird $h(\tau, \hspace{0.05cm}t_0)$ aber meist zeitdiskret angenommen („Echos”). | + | *Eine Besonderheit der 2D–Darstellung ist, dass die $t$–Achse stets zeitdiskret (bei Vielfachen von $T$) aufgetragen wird, während die $\tau$–Achse wie im gezeigten Beispiel zeitkontinuierlich sein kann. Im Mobilfunk wird $h(\tau, \hspace{0.05cm}t_0)$ aber meist auch zeitdiskret hinsichtlich $\tau$ angenommen („Echos”). |
| − | *Die LZV–Gleichung ist nur anwendbar, wenn die zeitliche Veränderung des Kanals (im Bild durch den Parameter $T$ gekennzeichnet) langsam erfolgt im Vergleich zur maximalen Verzögerung $\tau_{\rm max}$. Im Mobilfunk ist diese Bedingung ⇒ $\tau_{\rm max} < T$ fast immer erfüllt. | + | *Die LZV–Gleichung ist nur anwendbar, wenn die zeitliche Veränderung des Kanals (im Bild durch den Parameter $T$ gekennzeichnet) langsam erfolgt im Vergleich zur maximalen Verzögerung $\tau_{\rm max}$. Im Mobilfunk ist diese Bedingung ⇒ $\tau_{\rm max} < T$ fast immer erfüllt. |
| − | *Je nachdem, ob man das erste Fourierintegral auf den Parameter $\tau$ oder $t$ anwendet, kommt man zu unterschiedlichen Spektralfunktionen. In der [[Aufgabe_2.1Z:_2D-Frequenz-_und_2D-Zeitdarstellung|Aufgabe 2.1Z]] wird beispielsweise die zeitvariante '''2D–Übertragungsfunktion''' betrachtet: | + | *Je nachdem, ob man das erste Fourierintegral auf den Parameter $\tau$ oder $t$ anwendet, kommt man zu unterschiedlichen Spektralfunktionen. In der [[Aufgabe_2.1Z:_2D-Frequenz-_und_2D-Zeitdarstellung|Aufgabe 2.1Z]] wird beispielsweise die zeitvariante '''2D–Übertragungsfunktion''' betrachtet: |
::<math>H(f,\hspace{0.05cm} t) | ::<math>H(f,\hspace{0.05cm} t) | ||
Revision as of 16:01, 9 April 2019
Contents
# ÜBERBLICK ZUM ZWEITEN HAUPTKAPITEL #
Nach der Zeitvarianz wird nun der Begriff der Frequenzselektivität eingeführt und an Beispielen verdeutlicht, eine Kanaleigenschaft, die für die mobile Kommunikation ebenfalls von großer Bedeutung ist. Wie im gesamten Buch erfolgt die Beschreibung im äquivalenten Tiefpassbereich.
Im Einzelnen werden behandelt:
- der Unterschied zwischen zeitinvarianten und zeitvarianten Systemen,
- die zeitvariante Impulsantwort als wichtige Beschreibungsfunktion zeitvarianter Systeme,
- der Mehrwegeempfang als Ursache für frequenzselektives Verhalten,
- eine ausführliche Herleitung und Interpretation des GWSSUS–Kanalmodells,
- die Kenngrößen des GWSSUS–Modells: Kohärenzbandbreite, Korrelationsdauer, usw.
Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im Versuch „Mobilfunkkanal” des Praktikums „Simulation digitaler Übertragungssysteme”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Windows–Programm MFK ⇒ Link verweist auf die ZIP-Version des Programms und
- der zugehörigen Praktikumsanleitung ⇒ Link verweist auf die PDF-Version (58 Seiten).
Übertragungsfunktion und Impulsantwort
Die Beschreibungsgrößen eines Nachrichtenübertragungssystems wurden bereits in den Kapiteln Systembeschreibung im Frequenzbereich bzw. Systembeschreibung im Zeitbereich des Buches „Lineare zeitvariante Systeme” eingeführt und eingehend diskutiert. Die wichtigsten Ergebnisse sollen hier nochmals kurz zusammengefasst werden.
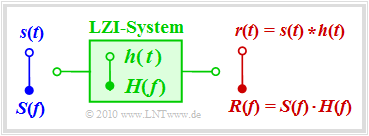
Vorausgesetzt wird zunächst ein lineares und zeitinvariantes System ⇒ LZI–System mit dem Signal $s(t)$ am Eingang und dem Ausgangssignal $r(t)$. Der Einfachheit halber seien $s(t)$ und $r(t)$ reell. Dann gilt:
- Das System lässt sich vollständig durch die Übertragungsfunktion $H(f)$ charakterisieren. Man bezeichnet $H(f)$ auch als den Frequenzgang. Definitionsgemäß gilt $H(f) = R(f)/S(f)$.
- Ebenso ist das System durch die Impulsantwort $h(t)$ als die Fourierrücktransformierte von $H(f)$ vollständig gekennzeichnet. Das Ausgangssignal ergibt sich aus der Faltung:
- \[r(t) = s(t) \star h(t) \hspace{0.4cm} {\rm mit} \hspace{0.4cm} h(t) \hspace{0.2cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.2cm} H(f) \hspace{0.05cm}.\]
Um die durch $H(f)$ bzw. $h(t)$ entstehenden linearen Verzerrungen zu erkennen, eignen sich die folgenden Eingangssignale:
- ein Diracimpuls: $s(t) = \delta(t)$ ⇒ $r(t) = h(t)$ ⇒ Impulsantwort,
- eine Sprungfunktion: $s(t) = \gamma(t)$ ⇒ $r(t) = \gamma(t) \star h(t)$ ⇒ Sprungantwort,
- ein Diracpuls: $s(t) = p_\delta(t)$ ⇒ $r(t) = p_\delta(t) \star h(t)$ ⇒ Pulsantwort.
Dagegen ist ein Gleichsignal $s(t) = A$ nicht geeignet, die Frequenzabhängigkeit des LZI–Systems sichtbar werden zu lassen. Bei einem Tiefpass–System wäre dann das Ausgangssignal unabhängig von $H(f)$ stets konstant: $r(t) = A \cdot H(f= 0)$.
Auf der nächsten Seite betrachten wir als Eingangssignal $s(t)$ einen Diracpuls $p_\delta(t)$. Hiermit lassen sich die Gemeinsamkeiten und Unterschiede zwischen zeitinvarianten und zeitvarianten Systemen sehr anschaulich darstellen.
Hinweis: Die Eigenschaften von $H(f)$ und $h(t)$ werden im Lernvideo Einige Anmerkungen zur Übertragungsfunktion ausführlich behandelt.
Zeitinvariante vs. zeitvariante Kanäle
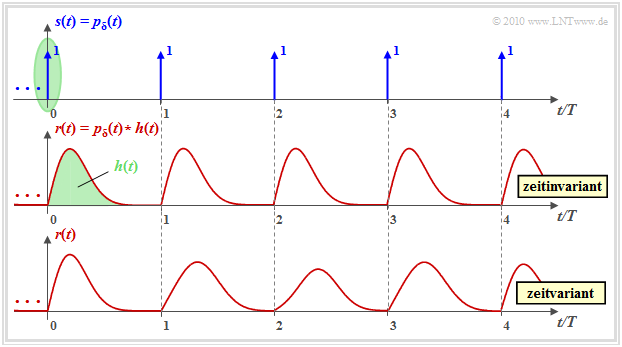
Die Grafik soll den Unterschied zwischen einem zeitinvarianten Kanal („LZI”) und einem zeitvarianten Kanal („LZV”) verdeutlichen.
Man erkennt aus dieser Darstellung:
- Das Sendesignal $s(t)$ ist hier ein Diracpuls $p_\delta(t)$, also eine unendliche Folge von Diracimpulsen in äquidistanten Abständen $T$, alle mit dem Gewicht $1$ (siehe obere Grafik):
- \[s(t) = p_{\rm \delta} (t) = \sum_{n = -\infty}^{+\infty} {\rm \delta} (t - n \cdot T) \hspace{0.05cm}.\]
- Grün markiert ist der Diracimpuls bei $t = 0$. Mit $s(t) = {\rm \delta}(t)$ ist das Signal am Kanalausgang gleich $r(t) = h(t)$ entsprechend der grünen Hinterlegung. Vorausgesetzt wird zunächst, dass die Ausdehnung der Impulsantwort $h(t)$ kleiner ist als $T$.
- Für das gesamte Empfangssignal nach dem LZI–Kanal gemäß der mittleren Grafik kann dann geschrieben werden:
- \[r(t) = p_{\rm \delta} (t) \star h(t) = \sum_{n = -\infty}^{+\infty} h (t - n \cdot T) \hspace{0.05cm}.\]
- Bei einem zeitvarianten Kanal ⇒ untere Grafik ist diese Gleichung nicht anwendbar. In jedem Zeitintervall ergibt sich nun nämlich eine andere Signalform.
$\text{Fazit:}$ Bei einem zeitvarianten Kanal kann man keine einparametrige Impulsantwort $h(t)$ und somit auch keine Übertragungsfunktion $H(f)$ angeben.
Hinweis: Das Lernvideo Eigenschaften des Übertragungskanals beschreibt die Unterschiede zwischen LZV– und LZI–Systemen.
Zweidimensionale Impulsantwort
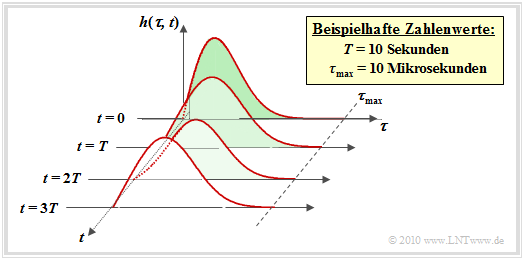
Zur Kennzeichnung einer zeitvarianten Impulsantwort verwendet man einen zweiten Parameter und bildet die Impulsantwort vorzugsweise in einem dreidimensionalen Koordinatensystem ab.
Voraussetzung hierfür ist, dass der Kanal weiterhin linear ist; man spricht dann von einem LZV–System (linear zeitvariant).
Es gelten folgende Zusammenhänge:
- \[\text{LZI:}\hspace{0.5cm} r(t) = \int_{-\infty}^{+\infty} h(\tau) \cdot s(t-\tau) \hspace{0.15cm}{\rm d}\tau \hspace{0.05cm},\]
- \[\text{LZV:}\hspace{0.5cm} r(t) \hspace{-0.1cm} = \hspace{-0.1cm} \int_{-\infty}^{+\infty} h(\tau, \hspace{0.1cm}t) \cdot s(t-\tau) \hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}.\]
Zur letzten Gleichung und obiger Grafik ist anzumerken:
- Der Parameter $\tau$ gibt die Verzögerungszeit zur Kennzeichnung der Zeitdispersion an. Durch Ausschreiben der Faltungsoperation ist es gelungen, dass $\tau$ auch der Parameter der LZI–Impulsantwort ist. Auf den letzten Seiten wurde noch von $h(t)$ gesprochen.
- Der zweite Parameter der Impulsantwort bzw. die zweite Achse kennzeichnet die absolute Zeit $t$, die unter anderem zur Beschreibung der Zeitvarianz herangezogen wird. Zu unterschiedlichen Zeiten $t$ hat die Impulsantwort $h(\tau, \hspace{0.05cm}t)$ eine andere Form.
- Eine Besonderheit der 2D–Darstellung ist, dass die $t$–Achse stets zeitdiskret (bei Vielfachen von $T$) aufgetragen wird, während die $\tau$–Achse wie im gezeigten Beispiel zeitkontinuierlich sein kann. Im Mobilfunk wird $h(\tau, \hspace{0.05cm}t_0)$ aber meist auch zeitdiskret hinsichtlich $\tau$ angenommen („Echos”).
- Die LZV–Gleichung ist nur anwendbar, wenn die zeitliche Veränderung des Kanals (im Bild durch den Parameter $T$ gekennzeichnet) langsam erfolgt im Vergleich zur maximalen Verzögerung $\tau_{\rm max}$. Im Mobilfunk ist diese Bedingung ⇒ $\tau_{\rm max} < T$ fast immer erfüllt.
- Je nachdem, ob man das erste Fourierintegral auf den Parameter $\tau$ oder $t$ anwendet, kommt man zu unterschiedlichen Spektralfunktionen. In der Aufgabe 2.1Z wird beispielsweise die zeitvariante 2D–Übertragungsfunktion betrachtet:
- \[H(f,\hspace{0.05cm} t) \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) \hspace{0.05cm}.\]
Aufgaben zum Kapitel
Aufgabe 2.1: Zweidimensionale Impulsantwort
Aufgabe 2.1Z: 2D-Frequenz- und 2D-Zeitdarstellung