Mobile Communications/Non-Frequency-Selective Fading With Direct Component

1. Mobile Communications
2. Time-Variant Transmission Channels
3. Non-Frequency-Selective Fading With Direct Component

• Previous page
• Next page

• Previous page
• Next page

Channel model and Rice PDF

The  \text{Rayleigh distribution}$]]  describes the mobile communication channel under the assumption that there is no direct path and thus the multiplicative factor  $z(t) = x(t) + {\rm j} \cdot y(t)$  is solely composed of diffusely scattered components. If a direct component  $($Line of Sight,  $\rm LoS)$  is present, it is necessary to add direct components   $x_0$  and/or  $y_0$  to the zero mean Gaussian processes   $x(t)$  and  $y(t)$: [[File:EN_Mob_T_1_4_S1.png|right|frame|Rice fading channel model|class=fit]] :\[x(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} x(t) +x_0 \hspace{0.05cm}, \hspace{0.2cm} y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} y(t) +y_0\hspace{0.05cm},\] :\[z(t) = x(t) + {\rm j} \cdot y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} z(t) +z_0 \hspace{0.05cm},\hspace{0.2cm} z_0 = x_0 + {\rm j} \cdot y_0\hspace{0.05cm}.\] The graph shows this  »'''Rice fading channel model'''«.  As a special case, the Rayleigh model results when   $x_0 = y_0= 0$. <br clear="all"> The Rice fading model can be summarized as follows, see also  [Hin08]'"`UNIQ--ref-00000008-QINU`"': *The real part  $x(t)$  is gaussian distributed with mean value  $x_0$  and variance  $\sigma ^2$. *The imaginary part  $y(t)$  is also gaussian distributed  $($mean  $y_0$,  equal variance  $\sigma ^2)$  and independent of  $x(t)$.<br> *For  $z_0 \ne 0$  the value  $|z(t)|$  has a [[Theory_of_Stochastic_Signals/Further_distributions#Rice_PDF|\text{Rice PDF}$, from which the term  "Rice fading"  is derived.

• To simplify the notation we set  $|z(t)| = a(t)$.   For  $a < 0$  it's PDF is  $f_a(a) \equiv 0$,  for  $a \ge 0$ the following equation applies, where  $\rm I_0(\cdot)$  denotes the  "modified Bessel–function" of zero order:

\[f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} \big [ -\frac{a^2 + |z_0|^2}{2\sigma^2}\big ] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.5cm}\text{with}\hspace{0.5cm}{\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u) = \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.\]

• The greater the direct path power  $(|z_0|^2)$  compared to the power of the stray components  $(2\sigma^2)$  the better suited for digital signal transmission is the mobile communication channel.

• If   $|z_0| \gg \sigma$  $($factor  $3$  or more$)$, the Rice PDF can be approximated accurately by a Gaussian distribution with mean  $|z_0|$  and variance  $\sigma^2$.
  

• In contrast to  Rayleigh fading   ⇒   $z_0 \equiv 0$, the phase at  Rice fading  is not equally distributed, but there is a preferred direction  $\phi_0 = \arctan(y_0/x_0)$.  Often one sets  $y_0 = 0$   ⇒   $\phi_0 = 0$.
  

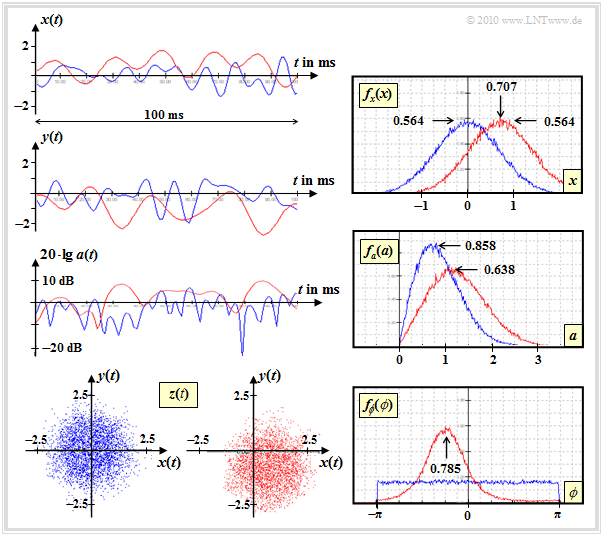
Example of signal behaviour with Rice fading

Comparison of Rayleigh fading (blue) and Rice fading (red)

The diagram shows typical signal characteristics and density functions of two mobile communication channels:

• Rayleigh fading  (blue curves)  with 

$${\rm E}\big [|z(t))|^2\big ] = 2 \cdot \sigma^2 = 1,$$

• Rice fading  (red curves)  with same  $\sigma$  and

$$x_0 = 0.707,\ \ y_0 = -0.707.$$

For the generation of the signals according to the above model, the  [[Mobile_Communications/Statistical_Bindings_within_the_Rayleigh_Process#Doppler_frequency_and_its_distribution|\text{maximum Doppler frequency}$]]  $f_\text{D, max} = 100 \ \rm Hz$  was used as reference. The auto-correlation function  $\rm (ACF)$  and power-spectral density  $\rm (PSD)$  of Rayleigh and Rice differ only slightly, other than adjusted parameter values.  The following applies: :\[\varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rice}} \hspace{-0.5cm} = \varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rayleigh}} \hspace{-0.8cm} + |z_0|^2 \hspace{0.05cm},\] :\[ {\it \Phi}_z(f_{\rm D})\Bigg |_{\hspace{0.1cm}{\rm Rice}} \hspace{-0.5cm} = {\it \Phi}_z(f_{\rm D})\Bigg |_{\hspace{0.1cm}{\rm Rayleigh}} \hspace{-0.8cm} + |z_0|^2 \cdot \delta (f_{\rm D}) \hspace{0.05cm}.\] It is taken into account that the spectral representation of a DC component leads to a Dirac delta function.<br> <br clear="all"> It should be noted about this graph: *The real parts  $x(t)$  of Rayleigh (blue) and Rice (red) only differ by the constant  $x_0 = 0.707$.   The statistical properties are otherwise the same:   Gaussian PDF $f_x(x)$  with standard deviation  $\sigma = 0.707$, either zero-mean (Rayleigh) or with mean  $x_0$  (Rice).<br> *In the imaginary part  $y(t)$  of the Rice distribution one can additionally recognize the direct component  $y_0 = -0.707$.  The (here not shown) PDF $f_y(y)$  is thus a Gaussian curve with the standard deviation  $\sigma = 0. 707$  around the mean value  $ y_0 = -0.707$, thus axisymmetrical to the shown PDF $f_x(x)$.<br> *The (logarithmic) representation of   ⇒   $a(t) =|z(t)|$ shows that the red curve is usually above the blue one.  This can also be read from the PDF $f_a(a)$ . *For the Rice channel, the error probability is lower than for Rayleigh when AWGN is taken into account, since the receiver gets some usable energy via the Rice direct path. *The PDF $f_\phi(\phi)$  shows the preferred angle  $\phi \approx -45^\circ$  of the given Rice channel   The complex factor  $z(t)$  is located mainly in the fourth quadrant because of  $x_0 > 0$  and  $y_0 < 0$ , whereas in the Rayleigh channel all quadrants are equally probable.

Exercises to the chapter

Exercise 1.6: Autocorrelation Function and PSD with Rice Fading

Exercise 1.6Z: Comparison of Rayleigh and Rice

Exercise 1.7: PDF of Rice Fading