Contents
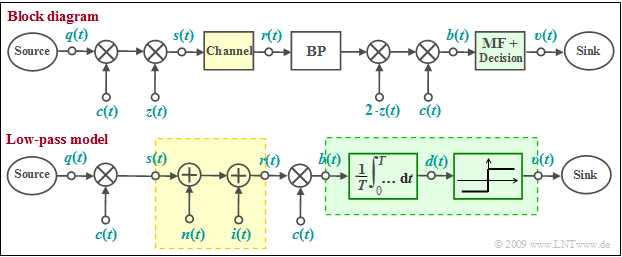
Block diagram and equivalent low-pass model
One possibility for realizing a CDMA system is the so-called direct-sequence spread spectrum, which is explained here on the basis of the block diagram. The corresponding model in the equivalent low-pass range is shown below.
In both models, the distortion-free channel $($AWGN and possibly interference from other users, but no intersymbol interference$)$ is highlighted in yellow and the optimal receiver $($matched filter plus threshold decider$)$ is highlighted in green.
$\text{This system can be characterized as follows:}$
- If the multiplication with the spread signal $c(t)$ at transmitter and receiver is omitted, the result is a conventional BPSK system with the carrier $z(t)$ and AWGN noise, characterized by the additive Gaussian interference signal $n(t)$. The second interference component (interference from other participants) is omitted: $i(t) = 0$.
- For the following it is assumed $($this is essential for direct-sequence spread spectrum!$)$ that the source signal $q(t)$ has a rectangular NRZ curve. Then the matched filter can be replaced by an integrator over a symbol duration $T$ ⇒ "Integrate & Dump". This is followed by the threshold decider.
Principle and properties of band spreading methods
In the following we consider direct-sequence spread spectrum in the equivalent low-pass range. Thus, the multiplication with the carrier signals $z(t)$ or $2\cdot z(t)$ is omitted.
- Characteristic for this type of modulation is the multiplication of the bipolar and rectangular digital signal $q(t)$ with a pseudo-random $±1$ spreading sequence $c(t)$:
- $$s(t) = q(t) \cdot c(t) \hspace{0.05cm}.$$
- The duration $T_c$ of a spreading chip is smaller than the duration $T$ of a source symbol by the integer spreading factor $J$, so that the transmitted signal spectrum is
- $$S(f) = Q(f) \star C(f)$$
- is wider than the spectral function $Q(f)$ by approximately this factor $J$ .
This process is referred to as Direct Sequence Spread Spectrum $\rm (DS–SS)$. In this context, please note in particular:
- In previous chapters, a major goal of modulation has always been to be as bandwidth-efficient as possible.
- Here, in contrast, we try to spread the signal over as wide a bandwidth as possible.
- The bandwidth expansion by $J$ is necessary to allow several subscribers to use the same frequency band simultaneously.
- Ideally, $2^J$ suitable spreading sequences can be found. This makes a CDMA system for $2^J$ simultaneous users feasible.
Band spreading techniques also offer the following advantages:
- One can transmit an additional low-rate "DS–SS signal" can be transmitted over a frequency band that is otherwise used by FDMA channels with a higher data rate without significantly disrupting the main applications. The band spread signal virtually disappears under the noise level of these signals.
- Targeted narrowband interferers ("sinusoidal interferers") can be combated well with this technique. This military point of view was also decisive for the invention and further development of band spreading techniques.
- Furthermore, the band spreading technique in general, but especially frequency hopping $($fast discrete change of the carrier frequency over a wide range$)$ and chirp modulation $($continuous change of the carrier frequency during a bit interval$)$ also offer the possibility of better transmission over frequency-selective channels.
Signal curves with a single participant
A disadvantage of direct-sequence spread spectrum modulation is that under unfavorable conditions interference can occur between the subscriber under consideration and other subscribers.
- This case is taken into account in the model by the interference quantity $i(t)$.
- We initially consider only one transmitter, so that $i(t) = 0$ is to be set.
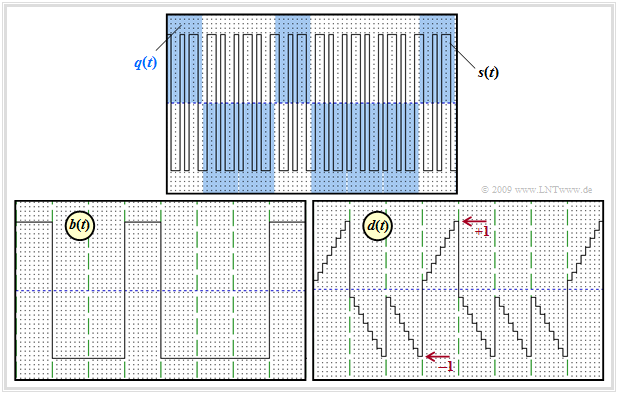
$\text{Example 1:}$
The graph shows
- above the source signal $q(t)$ – marked by the blue background – and the (band spread) transmitted signal $s(t)$,
- at the bottom left the signal $b(t)$ after band compression, and
- bottom right the detection signal $d(t)$ after the integrator, directly before the decision maker.
Further notes:
- A discrete-time and normalized signal representation with rectangles spaced by the chip duration $T_c$ is chosen.
- The spreading factor is $J = 8$.
- As spreading sequence the walsh function no. 7 is used.
- All images are valid for the noise-free case ⇒ $n(t) = 0$.
To the individual signal curves is to be noted:
- The $±1$ data signal $q(t)$ is marked by the blue background. After multiplication with the spread signal $c(t)$, the result is the transmitted signal $J = 8$ which is higher in frequency by the factor $s(t)$.
- The spread signal $c(t)$ is periodic with $T = J · T_c$ and thus has a line spectrum. In the first, fourth, and eighth data bits, $c(t)=s(t)$, but at the other times, $c(t) = - s(t)$.
- After band compression at the receiver, i.e., after chipsynchronous multiplication by $c(t) ∈ \{±1\}$ ⇒ $c^2(t) = 1$ , the signal $b(t)$ is obtained.
- In the distortion-free and noise-free case
- $$b(t) = r(t) \cdot c(t) = s(t) \cdot c(t) = \big [ q(t) \cdot c(t) \big ] \cdot c(t) = q(t) \hspace{0.05cm}.$$
- Integrating $b(t)$ over one bit at a time yields a linearly increasing or linearly decreasing signal $d(t)$. The step curve in the right image is solely due to the discrete-time representation.
- At the equidistant detection times the $ν$–th amplitude coefficients $a_ν$ of the source signal $q(t)$ are valid in the distortion- and noise-free case:
- $$ d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T}\hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t = a_\nu \in \{ +1, -1 \}\hspace{0.05cm}.$$
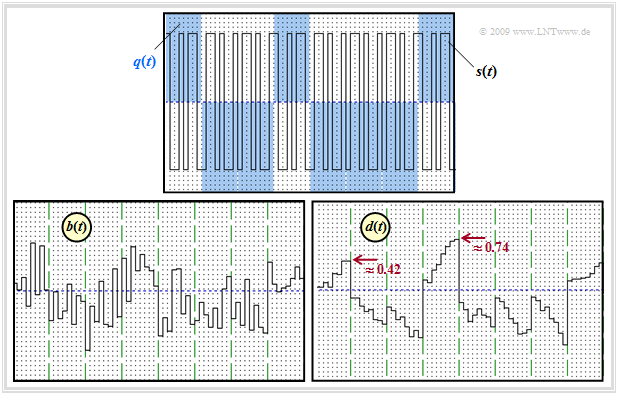
$\text{Example 2:}$
The two lower graphs change significantly from the first example when AWGN noise is considered.
The AWGN parameter is assumed to be $10 · \lg \ (E_{\rm B}/N_0) = 6 \ \rm dB$. Then
- das bandpassed signal $b(t)$ is no longer sectionally constant, and
- the detection signal $d(t)$ is no longer linearly increasing or decreasing.
Nach Schwellenwertentscheidung der Abtastwerte $d(νT)$ erhält man trotzdem meist die gesuchten Amplitudenkoeffizienten. Die vage Angabe „meist” ist durch die Bitfehlerwahrscheinlichkeit $p_{\rm B}$ quantifizierbar. Wegen
- $$b(t) = \big [ s(t) + n(t) \big ] \cdot c(t) = q(t) + n(t) \cdot c(t)$$
und aufgrund der Tatsache, dass die statistischen Eigenschaften von weißem Rauschen $n(t)$ durch die Multiplikation mit dem $±1$–Signal $c(t)$ nicht verändert werden, erhält man unabhängig vom Spreizgrad $J$ wieder das gleiche Ergebnis wie für die herkömmliche BPSK ohne Bandspreizung/Bandstauchung:
- $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B} }/{N_{\rm 0} } } \hspace{0.05cm} \right ) \hspace{0.05cm}.$$
Zusätzlicher Sinusstörer um die Trägerfrequenz
Wir gehen weiterhin von nur einem einzigen Teilnehmer aus. Im Unterschied zu der Berechnung im letzten Abschnitt gibt es aber nun
- neben dem AWGN–Rauschen $n(t)$ auch
- einen schmalbandiger Störer $i(t)$ um die Frequenz $f_{\rm I}$ mit der Leistung $P_{\rm I}$ und der Bandbreite $B_{\rm I}$.
Im Grenzfall $B_{\rm I} → 0$ lautet das Leistungsdichtespektrum dieses „Sinusstörers”:
- $${\it \Phi}_{\rm I}(f) = {P_{\rm I}}/{2} \cdot \big[ \delta ( f - f_{\rm I}) + \delta ( f + f_{\rm I}) \big ] \hspace{0.05cm}.$$
Bei einem herkömmlichen Übertragungssystem ohne Bandspreizung/Bandstauchung würde ein solcher Schmalbandstörer die Fehlerwahrscheinlichkeit in unzumutbarer Weise erhöhen. Bei einem System mit Bandspreizung ⇒ PN–Modulation ist der störende Einfluss deutlich geringer, da
- die Bandstauchung beim Empfänger hinsichtlich des Sinusstörers als Bandspreizung wirkt,
- sich dadurch dessen Leistung auf ein sehr breites Frequenzband $B_c = 1/T_c \gg B$ verteilt,
- die zusätzlich störende Leistungsdichte im Nutzfrequenzband $(±B)$ eher niedrig ist und durch eine geringfügige Erhöhung der AWGN–Rauschleistungsdichte $N_0$ erfasst werden kann.
Mit $T = J · T_c$ und $B = 1/T$ erhält man:
- $$p_{\rm B} \approx {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0} +P_{\rm I} \cdot T_c} } \hspace{0.05cm} \right ) = {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0} } \cdot \left( \frac{1}{1+ P_{\rm I} \cdot T_c/N_0}\right ) } \hspace{0.05cm} \right )\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{SNR–Degradation:} \ \frac{1}{\big[1 + P_{\rm I}/(J · N_0 · B)\big]}\hspace{0.05cm}.$$
Je größer der Spreizfaktor $J$ ist, desto geringer ist die Erhöhung der Rauschleistung durch den Sinusstörer.
Anmerkung: Diese Tatsache hat dazu geführt, dass in der Literatur der Spreizfaktor $J$ oft als Spreizgewinn bezeichnet wird, vergleiche beispielsweise [ZP85][1].
- In diesen Büchern geht es dabei meist um militärische Anwendungen der Bandspreizverfahren.
- Manchmal ist sogar vom „günstigsten Störer” die Rede, nämlich dann, wenn die Degradation am größten ist.
- Mit solchen Anwendungen wollen wir uns hier aber nicht befassen.
Näherungsweise kann aber die obige Gleichung der Fehlerwahrscheinlichkeit auch angewendet werden, wenn eine ungespreizte Übertragung höherer Datenrate und ein Bandspreiz–System geringer Rate im gleichen Frequenzband arbeiten. Der störende Einfluss des erstgenannten Systems mit Bandbreite $B_{\rm I}$ auf das Spread Spectrum System lässt sich näherungsweise als Schmalbandstörer behandeln, so lange $B_{\rm I}$ hinreichend klein ist.
$\text{Fazit:}$
- Bei AWGN–Rauschen (und auch vielen anderen Kanälen) lässt sich die Bitfehlerwahrscheinlichkeit durch Bandspreizung nicht verringern.
- Im günstigsten Fall ergibt sich mit Bandspreizung die gleiche Bitfehlerwahrscheinlichkeit wie bei BPSK (ohne Spreizung).
- In unserem Sinne ist Bandspreizung eine erforderliche Maßnahme, um mehrere Teilnehmer gleichzeitig im gleichen Frequenzband versorgen zu können.
- Wir betrachten im Folgenden ausschließlich den CDMA–Aspekt und sprechen deshalb auch weiterhin vom Spreizfaktor $J$ und nicht von einem Spreizgewinn.
Exercises for the chapter
Aufgabe 5.2: Bandspreizung und Schmalbandstörer
Aufgabe 5.2Z: Zur PN–Modulation
References
- ↑ Ziemer, R.; Peterson, R. L.: Digital Communication and Spread Spectrum Systems. New York: McMillon, 1985.