Difference between revisions of "Modulation Methods/General Model of Modulation"
m |
m |
||
| Line 11: | Line 11: | ||
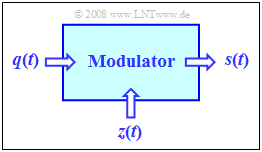
[[Modulation_Methods/Phasenmodulation_(PM)|Angle Modulation]] (WM &ndash from German "Winkelmodulation", including PM as well as FM) we will always consider the set-up shown in the image on the right. Here, the central block is the '''Modulator'''. | [[Modulation_Methods/Phasenmodulation_(PM)|Angle Modulation]] (WM &ndash from German "Winkelmodulation", including PM as well as FM) we will always consider the set-up shown in the image on the right. Here, the central block is the '''Modulator'''. | ||
| − | + | The two input signals and the output signal have the following characteristics: | |
| − | * | + | *The '''source signal''' $q(t)$ is the low frequency message signal and has the spectrum $Q(f)$. This signal is continuous in value and time and limited to the frequency range $|f| ≤ B_{\rm NF}$ (NF from German "Niederfrequenz" i.e. low frequency). |
| − | * | + | *The '''carrier signal''' $z(t)$ is a harmonic oscillation of the form |
:$$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t - \varphi_{\rm T})= A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}.$$ | :$$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t - \varphi_{\rm T})= A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}.$$ | ||
| − | * | + | *The '''transmission signal''' $s(t)$ is a higher frequency signal, whose spectral function $S(f)$ is in the range around the carrier frequency $f_{\rm T}$ liegt. |
| − | + | The modulator output signal $s(t)$ depends on both input signals $q(t)$ and $z(t)$ . The modulation methods considered below differ only by different combinations of $q(t)$ and $z(t)$. | |
| − | {{BlaueBox|TEXT=$\text{ | + | {{BlaueBox|TEXT=$\text{Definition:}$ Each [[ Signal_Representation/Harmonic_Oscillation|Harmonic Oscillation]] $z(t)$ can be described by |
| − | * | + | *the amplitude $A_{\rm T}$, |
| − | * | + | *the frequency $f_{\rm T}$ und |
| − | * | + | *the zero phase position ${\it ϕ}_{\rm T}$ . |
| − | + | Though the above left equation with a minus sign and ${\it ϕ}_{\rm T} is mostly used for the application of Fourier series and Fourier integrals, the right equation with ${\it ϕ}_{\rm T} = \ – φ_{\rm T}$ and a plus sign is more common for the description of modulation processes.}} | |
Revision as of 18:55, 10 November 2021
Joint description of amplitude and angle modulation
In the following two chapters Amplitude Modulation (AM) and Angle Modulation (WM &ndash from German "Winkelmodulation", including PM as well as FM) we will always consider the set-up shown in the image on the right. Here, the central block is the Modulator.
The two input signals and the output signal have the following characteristics:
- The source signal $q(t)$ is the low frequency message signal and has the spectrum $Q(f)$. This signal is continuous in value and time and limited to the frequency range $|f| ≤ B_{\rm NF}$ (NF from German "Niederfrequenz" i.e. low frequency).
- The carrier signal $z(t)$ is a harmonic oscillation of the form
- $$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t - \varphi_{\rm T})= A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}.$$
- The transmission signal $s(t)$ is a higher frequency signal, whose spectral function $S(f)$ is in the range around the carrier frequency $f_{\rm T}$ liegt.
The modulator output signal $s(t)$ depends on both input signals $q(t)$ and $z(t)$ . The modulation methods considered below differ only by different combinations of $q(t)$ and $z(t)$.
$\text{Definition:}$ Each Harmonic Oscillation $z(t)$ can be described by
- the amplitude $A_{\rm T}$,
- the frequency $f_{\rm T}$ und
- the zero phase position ${\it ϕ}_{\rm T}$ .
Though the above left equation with a minus sign and ${\it ϕ}_{\rm T} is mostly used for the application of Fourier series and Fourier integrals, the right equation with ${\it ϕ}_{\rm T} = \ – φ_{\rm T}$ and a plus sign is more common for the description of modulation processes.
<div style="clear:both;">
</div>
</div>
=='"`UNIQ--h-1--QINU`"'Eine sehr einfache, leider nicht immer ganz richtige Modulatorgleichung==
<br>
<div class="bluebox">
$\text{Definition:}$ Ausgehend von der harmonischen Schwingung (hier mit der Kreisfrequenz $ω_{\rm T} = 2πf_{\rm T}$ geschrieben)
:'"`UNIQ-MathJax2-QINU`"'
kommt man zur '''allgemeinen Modulatorgleichung''', indem die bisher festen Schwingungsparameter als zeitabhängig angesetzt werden:
:'"`UNIQ-MathJax3-QINU`"'
$\text{!! Vorsicht !!}$ Diese allgemeine Modulatorgleichung ist sehr einfach und plakativ und trägt zum Verständnis der Modulationsverfahren bei. Leider stimmt diese Gleichung bei der Frequenzmodulation nur in Ausnahmefällen. Hierauf wird im Kapitel [[Modulation_Methods/Frequenzmodulation_(FM)#Signalverl.C3.A4ufe_bei_Frequenzmodulation|Signalverläufe bei Frequenzmodulation]] noch ausführlich eingegangen.
<div style="clear:both;">
</div>
</div>
Als Sonderfälle sind in dieser Gleichung enthalten:
*Bei der '''Amplitudenmodulation''' $\rm (AM)$ ändert sich die zeitabhängige Amplitude $a(t)$ entsprechend dem Quellensignal $q(t)$, während die beiden anderen Signalparameter konstant sind:
:'"`UNIQ-MathJax4-QINU`"'
*Bei der '''Frequenzmodulation''' $\rm (FM)$ wird ausschließlich die momentane (Kreis–)Frequenz $\omega(t)$ durch das Quellensignal $q(t)$ bestimmt:
:'"`UNIQ-MathJax5-QINU`"'
*Bei der '''Phasenmodulation''' $\rm (PM)$ variiert die Phase $\phi(t)$ entsprechend dem Quellensignal $q(t)$:
:'"`UNIQ-MathJax6-QINU`"'
Bei diesen grundlegenden Verfahren werden also stets zwei der drei Schwingungsparameter konstant gehalten.
*Daneben gibt es auch Varianten mit mehr als einer Zeitabhängigkeit von Amplitude, Frequenz bzw. Phase.
*Ein Beispiel hierfür ist die [[Modulation_Methods/Einseitenbandmodulation|Einseitenbandmodulation]], bei der sowohl $a(t)$ als auch ${\it ϕ}(t)$ vom Quellensignal $q(t)$ beeinflusst werden.
=='"`UNIQ--h-2--QINU`"'Modulierte Signale bei digitalem Quellensignal==
<br>
Bei der Beschreibung von $\rm AM$, $\rm FM$ und $\rm PM$ wird meist das Quellensignal $q(t)$ als zeit- und wertkontinuierlich angenommen.
*Die obigen Gleichungen lassen sich aber auch auf ein rechteckförmiges Quellensignal anwenden.
*$q(t)$ ist in diesem Fall zeitkontinuierlich, aber wertdiskret. Damit sind auch [[Modulation_Methods/Lineare_digitale_Modulationsverfahren|Lineare digitale Modulationsverfahren]] beschreibbar.
<div class="greybox">
$\text{Beispiel 1:}$ Die Grafik zeigt oben ein rechteckförmiges Quellensignal $q(t)$ ⇒ ''Basisbandsignal'', und darunter gezeichnet die modulierten Signale $s(t)$, die sich bei wichtigen digitalen Modulationsverfahren ergeben.
[[File:EN_Mod_T_1_3_S3.png|right|frame|Basisbandsignal sowie $\rm ASK$, $\rm FSK$ und $\rm PSK$]]
*Bei der Amplitudenmodulation, deren digitale Variante unter der Bezeichnung ''Amplitude Shift Keying'' $\rm (ASK)$ bekannt ist, ist das Nachrichtensignal in der Hüllkurve von $s(t)$ zu erkennen.
*Im Signalverlauf der ''Frequency Shift Keying'' $\rm (FSK)$ werden die beiden möglichen Signalwerte von $q(t) = +1$ bzw. $q(t) =-1$ durch zwei unterschiedliche Frequenzen dargestellt.
*''Phase Shift Keying'' $\rm (PSK)$ führt bei Amplitudensprüngen des Quellensignals $q(t)$ zu Phasensprüngen im Signal $s(t)$, im binären Fall jeweils um $\pm π$ (bzw. $\pm 180^\circ$).
<div style="clear:both;">
</div>
</div>
=='"`UNIQ--h-3--QINU`"'Beschreibung des physikalischen Signals mit Hilfe des analytischen Signals==
<br>
Das modulierte Signal $s(t)$ ist bandpassartig. Wie bereits im Buch „Signaldarstellung” beschrieben wurde, wird ein solches BP–Signal $s(t)$ häufig durch das dazugehörige [[Signal_Representation/Analytical_Signal_and_Its_Spectral_Function|analytische Signa]]l $s_+(t)$ charakterisiert. Zu beachten ist:
*Das analytische Signal $s_+(t)$ erhält man aus dem reellen, physikalischen Signal $s(t)$, indem zu diesem als Imaginärteil dessen [[Signal_Representation/Analytical_Signal_and_Its_Spectral_Function#Darstellung_mit_der_Hilberttransformation|Hilberttransformierte]] hinzugefügt wird:
:'"`UNIQ-MathJax7-QINU`"'
*Das analytische Signal $s_+(t)$ ist somit stets komplex. Zwischen den beiden Zeitsignalen gilt der folgende einfache Zusammenhang:
:'"`UNIQ-MathJax8-QINU`"'
*Das Spektrum $S_+(f)$ des analytischen Signals ergibt sich aus dem zweiseitigen Spektrum $S(f)$, wenn man dieses bei positiven Frequenzen verdoppelt und für negative Frequenzen zu Null setzt:
:'"`UNIQ-MathJax9-QINU`"'
[[File:Mod_T_1_3_S4a_version2.png|right|frame| Verdeutlichung des analytischen Signals im Frequenzbereich]]
<div class="greybox">
$\text{Beispiel 2:}$ Die obere Grafik zeigt das Spektrum $S(f)$ eines reellen Zeitsignals $s(t)$. Man erkennt:
*Die Achsensymmetrie der Spektralfunktion $S(f)$ bezüglich der Frequenz $f=0$:
:'"`UNIQ-MathJax10-QINU`"'
*Hätte das Spektrum des reellen Zeitsignals $s(t)$ einen Imaginärteil, so wäre dieser punktsymmetrisch um $f=0$:
:'"`UNIQ-MathJax11-QINU`"'
<br clear="all">
Unten ist das Spektrum $S_+(f)$ des zugehörigen analytischen Signals $s_+(t)$ dargestellt. Dieses ergibt sich aus $S(f)$ durch
* Abschneiden der negativen Frequenzanteile: $S_+(f) \equiv 0$ für $f<0$,
*Verdoppeln der positiven Frequenzanteile: $S_+(f ) = 2 \cdot S(f )$ für $f \ge 0$.
Bis auf einen nicht praxisrelevanten Sonderfall ist das analytische Signal $s_+(t)$ stets komplex.
<div style="clear:both;">
</div>
</div>
Wir wenden nun diese Definitionen auf das modulierte Signal $s(t)$ an. Im Sonderfall $q(t) \equiv 0$ ist $s(t)$ wie das Trägersignal $z(t)$ eine harmonische Schwingung. Es gilt:
:'"`UNIQ-MathJax12-QINU`"'
Die zweite Gleichung beschreibt einen Drehzeiger mit folgenden Eigenschaften:
*Die Zeigerlänge kennzeichnet die Signalamplitude $A_{\rm T}$.
*Zur Zeit $t = 0$ liegt der Zeiger mit dem Winkel $ϕ_{\rm T}$ in der komplexen Ebene.
*Für $t > 0$ dreht der Zeiger mit konstanter Winkelgeschwindigkeit $ω_{\rm T}$ in mathematisch positive Richtung (entgegen dem Uhrzeigersinn).
*Die Zeigerspitze liegt stets auf einem Kreis mit dem Radius $A_{\rm T}$ und benötigt für eine Umdrehung genau die Periodendauer $T_0$.
[[File:P_ID963__Mod_T_1_3_S4_b_neu.png |right|frame| Verdeutlichung des analytischen Signals im Zeitbereich für $ϕ_{\rm T} = -45^\circ$]]
Um den Zusammenhang $s(t) = {\rm Re}[s_+(t)]$ im Querformat zeigen zu können, ist die komplexe Ebene entgegen der üblichen Darstellung um $90^\circ$ nach links gedreht:
'''Der Realteil ist nach oben und der Imaginärteil nach links aufgetragen'''.
<br clear="all">
Die einzelnen Modulationsverfahren lassen sich nun wie folgt darstellen:
*Bei der '''Amplitudenmodulation''' ändert sich die Zeigerlänge $a(t) = |s_+(t)|$ und damit die Hüllkurve von $s(t)$ entsprechend dem Quellensignal $q(t)$. <br>Die Winkelgeschwindigkeit $ω(t)$ ist dabei konstant.
*Bei der '''Frequenzmodulation''' ändert sich die Winkelgeschwindigkeit $ω(t)$ des rotierenden Zeigers entsprechend $q(t)$, <br>während die Zeigerlänge $a(t) = A_{\rm T}$ nicht verändert wird.
*Bei der '''Phasenmodulation''' ist die Phase $ϕ(t)$ zeitabhängig. <br>Es bestehen viele Gemeinsamkeiten mit der Frequenzmodulation, die ebenfalls zur Klasse der Winkelmodulation zählt.
=='"`UNIQ--h-4--QINU`"'Beschreibung des physikalischen Signals mit Hilfe des äquivalenten TP-Signals==
<br>
Manche Sachverhalte bezüglich der sendeseitigen Modulation und der Demodulation am Empfänger lassen sich anhand des [[Signal_Representation/Equivalent_Low_Pass_Signal_and_Its_Spectral_Function|äquivalenten Tiefpass–Signals]] entsprechend der Definition im Buch „Signaldarstellung” anschaulich am besten erklären.
Für dieses Signal $s_{\rm TP}(t)$ und dessen Spektrum $S_{\rm TP}(f)$ gelten die folgenden Aussagen:
[[File:Mod_T_1_3_S5a_version2.png|right|frame|Zum äquivalenten Tiefpass–Signal im Frequenzbereich]]
*Das Spektrum $S_{\rm TP}(f)$ des äquivalenten Tiefpass–Signals erhält man aus $S_+(f)$ durch Verschiebung um $f_{\rm T}$ nach links und liegt somit im Bereich um die Frequenz $f =0$:
:'"`UNIQ-MathJax13-QINU`"'
*Für die zugehörige Zeitfunktion gilt nach dem [[Signal_Representation/Fourier_Transform_Laws#Verschiebungssatz|Verschiebungssatz]]:
:'"`UNIQ-MathJax14-QINU`"'
*Das äquivalente Tiefpass–Signal einer unmodulierten harmonischen Schwingung ist für alle Zeiten konstant – die Ortskurve besteht in diesem Sonderfall aus einem einzigen Punkt:
:'"`UNIQ-MathJax15-QINU`"'
:'"`UNIQ-MathJax16-QINU`"'
<br clear="all">
<div class="bluebox">
$\text{Wichtiges Ergebnis:}$ Für ein amplituden– oder phasenmoduliertes Signal mit der Trägerfrequenz $f_{\rm T}$ gilt dagegen:
:'"`UNIQ-MathJax17-QINU`"'
Die Hüllkurve $a(t)$ und der Phasenverlauf $ϕ(t)$ des (physikalischen) Bandpass-Signals $s(t)$ bleiben auch im äquivalenten TP–Signal $s_{\rm TP}(t)$ erhalten.
<div style="clear:both;">
</div>
</div>
<div class="greybox">
$\text{Beispiel 3:}$ Die Grafik zeigt jeweils rechts das modulierte Signal $s(t)$ ⇒ roter Signalverlauf im Vergleich zum Trägersignal $z(t)$ ⇒ blauer Signalverlauf. <br>Links dargestellt sind die jeweiligen äquivalenten Tiefpass–Signale $s_{\rm TP}(t)$ ⇒ grüne Ortskurven.
[[File:EN_Mod_T_1_3_S5b.png |right|frame| Sendesignale bei Amplituden– und Winkelmodulation]]
Oben ist die '''Amplitudenmodulation''' beschrieben, bei der das Quellensignal $q(t)$ in der Hüllkurve $a(t)$ zu erkennen ist:
*Da die Nulldurchgänge des Trägers $z(t)$ erhalten bleiben, ist $ϕ(t) = 0$ und das äquivalente TP–Signal $s_{\rm TP}(t) = a(t)$ reell.
*Die Herleitung dieses Sachverhalts erfolgt im Kapitel [[Modulation_Methods/Hüllkurvendemodulation#Beschreibung_mit_Hilfe_des_.C3.A4quivalenten_TP.E2.80.93Signals|Beschreibung mit Hilfe des äquivalenten TP-Signals]].
Unten ist die '''Winkelmodulation''' verdeutlicht.
*Hier ist die Hüllkurve $a(t)$ konstant ⇒ das äquivalente TP-Signal $s_{\rm TP}(t) = A_{\rm T} · e^{\rm j·ϕ(t)}$ beschreibt einen Kreisbogen.
* Die Information über das Nachrichtensignal $q(t)$ steckt hier in der Lage der Nulldurchgänge von $s(t)$.
*Genaueres hierüber finden Sie im Kapitel [[Modulation_Methods/Phasenmodulation_(PM)#Gemeinsamkeiten_zwischen_Phasen.E2.80.93_und_Frequenzmodulation|Gemeinsamkeiten zwischen PM und FM]]
<div style="clear:both;">
</div>
</div>
''Hinweise:''
*Wir bezeichnen im Folgenden den zeitabhängigen Verlauf von $s_{\rm TP}(t)$ in der komplexen Ebene auch als "'''Ortskurve'''", während das "'''Zeigerdiagramm'''" den Verlauf des analytischen Signals $s_+(t)$ beschreibt.
- Der hier dargelegte Sachverhalt wird mit zwei interaktiven Applets im Zeitbereich verdeutlicht:
Aufgaben zum Kapitel
Aufgabe 1.4: Zeigerdiagramm und Ortskurve
Aufgabe 1.4Z: Darstellungsformen von Schwingungen