Contents
The Set of Real Numbers
In the following chapters of this book, complex quantities always play an important role. Although calculating with complex numbers is already treated and practiced in school mathematics, our experience has shown that even students of natural sciences and technical subjects have problems with it. Perhaps these difficulties are also related to the fact that "complex" is often used as a synonym for "complicated" in everyday life, while "real" stands for "reliable, honest and truthful" according to the Duden dictionary.
Therefore, the calculation rules for complex numbers are briefly summarized here at the end of this first basic chapter.
First there are some remarks about real quantities of numbers, for which in the strict mathematical sense the term "number field" would be more correct. These include:
$\text{Definitionen:}$
- Natural Numbers $\mathbb{N} = \{1, 2, 3, \text{...}\hspace{0.05cm} \}$. Using these numbers, for $n, \ k \in \mathbb{N}$ the arithmetic operations „addition” $(m = n +k)$, „multiplication” $(m = n \cdot k)$ and „power formation” $(m = n^k)$ are possible. The respective result of a calculation is again a natural number: $m \in \mathbb{N}$.
- Total Numbers $\mathbb{Z} = \{\text{...}\hspace{0.05cm} , -3, -2, -1, \ 0, +1, +2, +3, \text{...}\hspace{0.05cm}\}$. This set of numbers is an extension of the natural numbers $\mathbb{N}$. The introduction of the set $\mathbb{Z}$ was necessary to capture the result set of a subtraction $(m = n -k)$ for example $5 - 7 = - 2$.
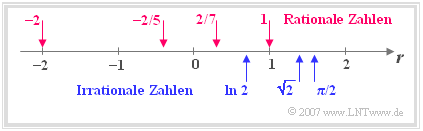
- Rational Numbers $\mathbb{Q} = \{z/n\}$ with $z \in \mathbb{Z}$ and $n \in \mathbb{N}$. With this set of numbers, also known as fractions, there is a defined result for each division. If you write a rational number in decimal notation, only zeros appear after a certain decimal place $($Example: $-2/5 = -0.400\text{...}\hspace{0.05cm})$ or periodicities $($Example: $2/7 = 0.285714285\text{...}\hspace{0.05cm})$. Since $n = 1$ is allowed, the integers are a subset of the rational numbers: $\mathbb{Z} \subset \mathbb{Q}$.
- Irrational Numbers $\mathbb{I} \neq {z/n}$ mit $z \in \mathbb{Z}$, $n \in \mathbb{N}$. Although there are infinite rational numbers, there are still infinite numbers which cannot be represented as a fraction. Examples are the number $\pi = 3.141592654\text{...}\hspace{0.05cm}$ (where there are no periods even with more decimal places) or the result of the equation $a^{2}=2 \,\,\Rightarrow \;\;a=\pm \sqrt{2}=\pm1.414213562\text{...}\hspace{0.05cm}$. This result is also irrational, which has already been proved by Euclid in antiquity.
- Real Numbers $\mathbb{R} = \mathbb{Q} \cup \mathbb{I}$ as the sum of all rational and irrational numbers.
- These can be ordered according to their numerical values and can be drawn on the so called number line as shown in the adjacent graph.
Imaginary and Complex Numbers
With the introduction of the irrational numbers the solution of the equation $a^2-2=0$ was possible, but not the solution of the equation $a^2+1=0$.
The mathematician Leonhard Euler solved this problem by extending the set of real numbers by the imaginary numbers . He defined the imaginary unit as follows:
- $${\rm j}=\sqrt{-1} \ \Rightarrow \ {\rm j}^{2}=-1.$$
It should be noted that Euler called this quantity „$\rm i$” and this is still common in mathematics today. In electrical engineering, on the other hand, the designation „$\rm j$” has become generally accepted since „$\rm i$” is already occupied by the time-dependent current.
$\text{Definition:}$ The complex number $z$ is generally the sum of a real number $x$ and an imaginary number ${\rm j} \cdot y$:
- $$z=x+{\rm j}\cdot y.$$
$x$ and $y$ are derived from the quantity $\mathbb{R}$ from the real numbers. The set of all possible complex numbers is called the body $\mathbb{C}$ of the complex numbers.
The number line of real numbers now becomes the complex plane, which is spanned by two number strings twisted by $90^\circ$ for real– and imaginary part.
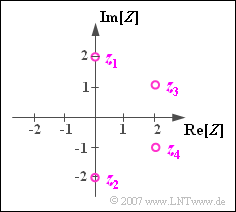
$\text{Beispiel 1:}$ The complex number $z_1 = 2 \cdot {\rm j}$ is one of two possible solutions of the equation $z^2+4=0$. The other solution is $z_2 = -2 \cdot {\rm j}$.
In contrast $z_3 = 2 + {\rm j}$ and $z_4 = 2 -{\rm j}$ give the two solutions to the following equation:
- $$(z-2- {\rm j})(z-2+ {\rm j}) = 0 \; \ \Rightarrow \;\ z^{2}-4 \cdot z+5=0.$$
$z_4 = z_3^\ast$ is also called the Complex Conjugate of $z_3$.
- The sum $z_3 + z_4$ is real:
- $$z_3 + z_4 = 2 \cdot {\rm Re}[z_3]=2 \cdot {\rm Re}[z_4].$$
- The difference $z_3 - z_4$ is purely imaginary:
- $$z_3 - z_4 = {\rm j} \cdot \big [2 \cdot {\rm Im}[z_3] \big ] ={\rm j} \cdot \big [-2 \cdot {\rm Im}[z_4] \big ].$$
Note: In the literature, complex quantities are often marked by underlining. This is not used in the $\rm LNTwww$–books.
Representation by Amount and Phase
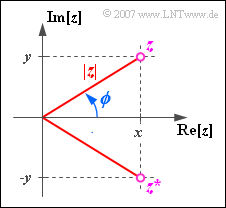
A complex number $z$ can be described not only by the real part $x$ and the imaginary part $y$ but also by its amount $|z|$ and the phase $\phi$ .
The following conversions apply:
- $$\left | z \right | = \sqrt{x^{2}+y^{2}}, \hspace{0.6cm}\phi = \arctan ({y}/{x}),$$
- $$x = |z| \cdot \cos(\phi), \hspace{0.6cm} y = |z| \cdot \sin(\phi ).$$
Thus the complex size $z$ can also be displayed in the following form
- $$z = |z| \cdot \cos (\phi) + {\rm j} \cdot |z| \cdot \sin (\phi) = |z| \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \phi}.$$
Hierbei wurde der Satz von Euler verwendet, der unten bewiesen wird. Dieser besagt, dass die komplexe Größe $ {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \phi}$ den Realteil $\cos(\phi)$ und den Imaginärteil $\sin(\phi)$ aufweist.
Weiter erkennt man aus der Grafik, dass für die Konjugiert-Komplexe von $z = x + {\rm j}\cdot y$ gilt:
- $$z^{\star} = x - {\rm j} \cdot y = |z| \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}\phi}.$$
$\text{Beweis des Eulerschen Satzes:}$ Dieser basiert auf dem Vergleich von Potenzreihenentwicklungen.
- Die Reihenentwicklung der Exponentialfunktion lautet:
- $${\rm e}^{x} = 1 + \frac{x}{1!}+ \frac{x^2}{2!}+ \frac{x^3}{3!} + \frac{x^4}{4!} +\text{ ...} \hspace{0.15cm}.$$
- Mit imaginärem Argument kann hierfür auch geschrieben werden:
- $${\rm e}^{ {\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}x} = 1 + {\rm j} \cdot \frac{x}{1!}+ {\rm j}^2 \cdot \frac{x^2}{2!}+ {\rm j}^3 \cdot \frac{x^3}{3!} + {\rm j}^4 \cdot \frac{x^4}{4!} + \text{ ...} \hspace{0.15cm}.$$
- Berücksichtigt man \({\rm j}^{2}=-1, \ \ {\rm j}^{3} = -{\rm j},\ \ {\rm j}^{4} = 1, \ \ {\rm j}^{5} = {\rm j}, \text{ ...} \hspace{0.15cm}\) und fasst die reellen und die imaginären Terme zusammen, so erhält man
- $${\rm e}^{ {\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}x} = A(x) + {\rm j}\cdot B(x).$$
- Für die beiden Reihen gilt dabei:
- $$A(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!}+ \text{ ...} \hspace{0.1cm}= \cos(x),\hspace{0.5cm} B(x) = \frac{x}{1!}- \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!}+ \text{ ...}= \sin(x).$$
- Daraus folgt direkt der Satz von Euler:
- $${\rm e}^{ {\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}x} = \cos (x) + {\rm j} \cdot \sin (x) \hspace{2cm} \rm q.e.d.$$
Rechenregeln für komplexe Zahlen
Die Rechengesetze für zwei komplexe Zahlen
- $$z_1 = x_1 + {\rm j} \cdot y_1 = |z_1| \cdot {\rm e}^{{\rm j}\hspace {0.05cm}\cdot \hspace {0.05cm} \phi_1}, \hspace{0.5cm} z_2 = x_2 + {\rm j} \cdot y_2 = |z_2| \cdot {\rm e}^{{\rm j} \hspace {0.05cm}\cdot \hspace {0.05cm} \phi_2}$$
sind derart definiert, dass sich für den Sonderfall eines verschwindenden Imaginärteils die Rechenregeln der reellen Zahlen ergeben. Man spricht vom so genannten Permanenzprinzip.
Für die Grundrechenarten gelten folgende Regeln:
- Die Summe zweier komplexer Zahlen (bzw. deren Differenz) wird gebildet, indem man ihre Real- und Imaginärteile addiert (bzw. subtrahiert):
- \[z_3 = z_1 + z_2 = (x_1+x_2) + {\rm j}\cdot (y_1 + y_2),\]
- \[z_4 = z_1 - z_2 = (x_1-x_2) + {\rm j}\cdot (y_1 - y_2).\]
- Das Produkt zweier komplexer Zahlen kann in der Realteil- und Imaginärteildarstellung durch Ausmultiplizieren unter Berücksichtigung von \({\rm j}^{2}=-1\) gebildet werden. Einfacher gestaltet sich die Multiplikation allerdings, wenn \(z_1\) und \(z_2\) mit Betrag und Phase geschrieben werden:
- \[z_5 = z_1 \cdot z_2 = (x_1\cdot x_2 - y_1\cdot y_2) + {\rm j}\cdot (x_1\cdot y_2 + x_2\cdot y_1),\]
- \[z_5 = |z_1| \cdot {\rm e}^{{\rm j} \hspace {0.05cm}\cdot \hspace {0.05cm} \phi_1} \cdot |z_2| \cdot {\rm e}^{{\rm j}\hspace {0.05cm}\cdot \hspace {0.05cm} \phi_2}= |z_5| \cdot {\rm e}^{{\rm j} \hspace {0.05cm}\cdot \hspace {0.05cm} \phi_5} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} |z_5| = |z_1| \cdot |z_2| , \hspace{0.3cm}\phi_5 = \phi_1 + \phi_2 .\]
- Die Division ist in der Exponentialschreibweise ebenfalls überschaubarer. Die beiden Beträge werden dividiert und die Phasen im Exponenten subtrahiert:
- \[z_6 = \frac{z_1}{z_2} = |z_6| \cdot {\rm e}^{{\rm j} \hspace {0.05cm}\cdot \hspace {0.05cm} \phi_6} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} |z_6| = \frac{|z_1|}{|z_2|}, \hspace{0.3cm}\phi_6 = \phi_1 - \phi_2 .\]
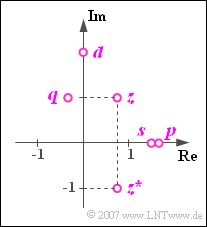
$\text{Beispiel 2:}$ In der Grafik sind als Punkte innerhalb der komplexen Ebene dargestellt:
- die komplexe Zahl \(z=0.75 + {\rm j} = 1.25 \cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.03cm} \cdot \hspace{0.05cm}53.1^{\circ} }\),
- deren Konjugiert-Komplexe \(z^{\ast} = 0.75 - {\rm j} = 1.25 \cdot {\rm e}^{ - {\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}53.1^{\circ} }\),
- die Summe \(s=z+z^{\ast}=1.5\) (rein reell),
- die Differenz \(d=z-z^{\ast}=2 \cdot {\rm j}\) (rein imaginär),
- das Produkt \(p=z \cdot z^{\ast} = 1.25^{2} \approx 1.5625\) (ebenfalls rein reell),
- der Quotient \(q= {z}/{z^{\ast} }={\rm e}^{\hspace{0.05cm} {\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}106.2^{\circ} }\) mit Betrag $1$ und dem doppelten Phasenwinkel von $z$.
Die Thematik dieses Kapitels wird ausführlich im Lernvideo Rechnen mit komplexen Zahlen behandelt.
Aufgaben zum Kapitel
Aufgabe 1.3: Rechnen mit komplexen Zahlen
Aufgabe 1.3Z: Nochmals komplexe Zahlen