Difference between revisions of "Signal Representation/Differences and Similarities of Low-Pass and Band-Pass Signals"
| Line 40: | Line 40: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Example 1: | + | $\text{Example 1 : To classify signals with respect to „low pass” and „bandpass”}$ |
| − | '''(a)''' '' | + | '''(a)''' ''speech'' and ''music'' are low-pass signals with a bandwidth of $\text{20 kHz}$ (at very good quality). Since a radio transmission is only possible from approx. $\text{100 kHz}$ , a conversion to carrier frequencies between |
| − | *$\text{0.525 ... 1.61 MHz}$ $($ | + | *$\text{0.525 ... 1.61 MHz}$ $($Medium wave broadcasting, amplitude modulation, channel spacing $\text{9 kHz})$, |
| − | *$\text{87.5 ... 108 MHz}$ $($ | + | *$\text{87.5 ... 108 MHz}$ $($Radio on FM, frequency modulation, channel spacing $\text{300 kHz})$ |
| + | is needed. | ||
| − | '''(b)''' ''TV | + | '''(b)''' ''TV image signals'' have a larger bandwidth, for example $\text{5 MHz}$ . Here, as well, a frequency band shift occurs before the sound and image transmission due to carrier frequencies between |
| − | *$\text{41 ... 68 / 174 ... 230 MHz}$ ( | + | *$\text{41 ... 68 / 174 ... 230 MHz}$ (television, VHF band, channel spacing $\text{7 MHz})$, |
| − | *$\text{470 ... 850 MHz}$ $($ | + | *$\text{470 ... 850 MHz}$ $($television, UHF band, channel spacing $\text{8 MHz})$. |
| + | '''(c)''' With ''GSM mobile radio'' the carrier frequencies in the D-band are $\text{900 MHz}$ and in the D-band $\text{1800 MHz}$. | ||
| − | '''( | + | '''(d)''' With ''optical transmission'' the electrical signals are converted into light, i.e. to frequencies between ca. $\text{200 THz}$ and $\text{350 THz}$ $($correspondingly $\text{1.55 µm ... 0.85 µm}$ Wavelength).}} |
| − | |||
| − | + | ==Properties of BP-Signals== | |
| − | == | ||
<br> | <br> | ||
| − | + | On this page - without claiming to be complete - some characteristics of bandpass signals are compiled and compared to lowpass signals. We start from the spectral functions $X_{\rm TP}(f)$ and $X_{\rm BP}(f)$ according to the following sketch. | |
| − | [[File:P_ID679__Sig_T_4_1_S2a_neu.png|center|frame| | + | [[File:P_ID679__Sig_T_4_1_S2a_neu.png|center|frame|Low Pass- and Bandpass Spectrum]] |
| − | + | Regarding the graphic is to be remarked: | |
| − | * | + | *The triangular shape of the displayed spectra is to be understood schematically and is only to mark the occupied frequency band. So it should not be concluded that all frequencies within the band are actually occupied and that all spectral functions increase linearly with frequency $f$ . |
| − | * | + | *The corresponding time functions $x_{\rm TP}(t)$ and $x_{\rm BP}(t)$ are real for the time being. This means that according to the [[Signal_Representation/Fourier_Transform_Laws#Zuordnungssatz|Mapping Theorem]] the spectral functions $X_{\rm TP}(f)$ and $X_{\rm BP}(f)$ - related to the frequency $f = 0$ - each have an even real part and an odd imaginary part. |
| − | * | + | *As bandwidth $B_{\rm TP}$ or. $B_{\rm BP}$ for both low pass and bandpass we refer to the occupied frequency band at the positive frequencies (in the graphic: continuous curves). |
| + | *As bandwidth $B_{\rm TP}$ or. $B_{\rm BP}$ for lowpass and bandpass we equally denote the occupied frequency band at the positive frequencies (in the graphic: continuous curves). | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ An example with discrete spectral lines follows. The left graph shows the spectrum $Q(f)$ of the message signal |
:$$q(t) = 3\hspace{0.05cm}{\rm V} + 4\hspace{0.05cm}{\rm V} \cdot \cos (2 \pi \cdot 3\hspace{0.05cm}{\rm kHz} \cdot t) + 2\hspace{0.05cm}{\rm V} \cdot \sin (2 \pi \cdot 4\hspace{0.05cm}{\rm kHz} \cdot t). $$ | :$$q(t) = 3\hspace{0.05cm}{\rm V} + 4\hspace{0.05cm}{\rm V} \cdot \cos (2 \pi \cdot 3\hspace{0.05cm}{\rm kHz} \cdot t) + 2\hspace{0.05cm}{\rm V} \cdot \sin (2 \pi \cdot 4\hspace{0.05cm}{\rm kHz} \cdot t). $$ | ||
| − | + | The discrete spectral lines of the real part ⇒ ${\rm Re}\big[Q(f)\big]$ are shown in blue and those of the imaginary part ⇒ ${\rm Im}\big[Q(f)\big]$ in red. | |
| + | |||
| + | [[File:P_ID698__Sig_T_4_1_S2b_neu.png|center|frame|Example of a Low Pass- and Bandpass-Spectrum]] | ||
| − | [[ | + | On the right is the spectrum $S(f)$ after single sideband amplitude modulation (ESB-AM) with the carrier frequency $f_{\rm T} = 100 \,\text{kHz}$. A description of this transmission system can be found in chapter [[Modulation_Methods/Hüllkurvendemodulation|Envelope Demodulation]] of the book „Modulation Methods”. |
| + | *According to this description, $q(t)$ is uniquely a low-pass signal and $s(t)$ is a band-pass signal. The bandwidths are $B_{\rm TP} = B_{\rm BP} = 4 \,\text{kHz}$. | ||
| + | *If the DC component $(3 \,\text{V})$ would be missing in the source signal, then $q(t)$ would still be described as low-pass filter-like. | ||
| + | *Without knowledge of the task, one could interpret $q(t)$ but then also as a bandpass signal with the bandwidth $B_{\rm BP} = 1 \,\text{kHz}$ . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | This example shows that there is no clear mathematical distinction between low pass and band pass signals.}} | ||
| − | == | + | ==Description of a BP-Signal with TP-Signals== |
<br> | <br> | ||
| − | + | We consider two low pass spectra $X_1(f)$ and $X_2(f)$ with the bandwidths $B_1$ and $B_2$ corresponding to the left graph. | |
[[File:P_ID684__Sig_T_4_1_S3a.png|center|Erzeugung eines Bandpass-Spektrums aus Tiefpass-Spektren]] | [[File:P_ID684__Sig_T_4_1_S3a.png|center|Erzeugung eines Bandpass-Spektrums aus Tiefpass-Spektren]] | ||
| − | + | You can see from this diagram: | |
| − | * | + | *If $X_1(f)$ and $X_2(f)$ up to a frequency $f_{12}$ are identical, the difference describes a bandpass spectrum with bandwidth $B_{\rm BP} = B_1 - f_{12}$. According to the graphic on the right, the following then applies |
:$$X_{\rm BP}(f) = X_1(f) -X_2(f).$$ | :$$X_{\rm BP}(f) = X_1(f) -X_2(f).$$ | ||
| − | * | + | *Due to the linearity of the Fourier transform, the time function associated with the bandpass spectrum $X_{\rm BP}(f)$ is valid |
:$$x_{\rm BP}(t) = x_1(t) - x_2(t).$$ | :$$x_{\rm BP}(t) = x_1(t) - x_2(t).$$ | ||
| − | * | + | *It generally follows from the Fourier transformation that the integral over the time function is equal to the spectral value at $f = 0$ . Consequently, this integral is always zero for every bandpass signal: |
:$$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm | :$$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm | ||
d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$ | d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$ | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ |
| − | + | The red curves in the two graphs show the bandpass spectrum $X_{\rm BP}(f)$ and the corresponding time function | |
:$$x_{\rm BP}(t) = 10\hspace{0.05cm}{\rm | :$$x_{\rm BP}(t) = 10\hspace{0.05cm}{\rm | ||
| Line 113: | Line 114: | ||
\hspace{0.05cm}{\rm kHz} \cdot t).$$ | \hspace{0.05cm}{\rm kHz} \cdot t).$$ | ||
| − | [[File:EN_Sig_T_4_1_S3a.png|center|frame| | + | [[File:EN_Sig_T_4_1_S3a.png|center|frame|Low Pass– and Bandpass–Spectrum and Their Signals]] |
| − | + | Also shown are the two low-pass spectra and signals. You can see from these pictures: | |
| − | * | + | *The blue-dotted curve in the left graph represents the trapezoidal spectrum $X_1(f)$ where the equivalent bandwidth $\Delta f_1= 10 \,\text{kHz}$ and the rolloff factor $r_1 = 0.2$ is |
| − | * | + | *The blue-dotted curve in the right graphic shows the corresponding low pass–signal $x_1(t)$. The signal value at $t = 0$ corresponds to the blue trapezoidal area of the spectrum $X_1(f)$: |
:$$x_1(t = 0) = 10 \,\text{V}.$$ | :$$x_1(t = 0) = 10 \,\text{V}.$$ | ||
| − | * | + | *The green curve applies to the rectangular spectrum $X_2(f)$ with the equivalent bandwidth $\Delta f_2= 2 \,\text{kHz}$. The corresponding time signal $x_2(t)$ runs $\sin(x)/x$-shaped and is valid: |
:$$x_2(t = 0) = 2 \,\text{V}.$$ | :$$x_2(t = 0) = 2 \,\text{V}.$$ | ||
| − | + | The red curve for the bandpass-like signal is the difference between the blue and green curve on the left and right. Accordingly | |
:$$x_{\rm BP}(t = 0) = x_1(t = 0) - x_2(t = 0) = 8 \,\text{V},$$ | :$$x_{\rm BP}(t = 0) = x_1(t = 0) - x_2(t = 0) = 8 \,\text{V},$$ | ||
:$$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm | :$$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm | ||
| Line 127: | Line 128: | ||
| − | == | + | ==BP-Signal Synthesis from Equivalent TP-Signals== |
<br> | <br> | ||
| − | + | We consider a low-pass signal $x_{\rm TP}(t)$ with spectrum $X_{\rm TP}(f)$ according to the left sketch. | |
| + | |||
| + | If this signal is multiplied by a (dimensionless) harmonic oscillation | ||
| − | |||
| − | |||
:$$z(t) = {\cos} ( 2\pi \cdot f_{\rm T} \cdot | :$$z(t) = {\cos} ( 2\pi \cdot f_{\rm T} \cdot | ||
t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\hspace{0.15cm} Z(f) = {1}/{2}\cdot | t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\hspace{0.15cm} Z(f) = {1}/{2}\cdot | ||
\delta (f - f_{\rm T})+ {1}/{2}\cdot \delta (f + f_{\rm T}),$$ | \delta (f - f_{\rm T})+ {1}/{2}\cdot \delta (f + f_{\rm T}),$$ | ||
| − | + | the convolution theorem for the spectrum of the signal $x_{\rm BP}(t) = x_{\rm TP}(t) yields \cdot z(t)$: | |
:$$X_{\rm BP}(f) = X_{\rm TP}(f)\star Z(f) = {1}/{2}\cdot X_{\rm | :$$X_{\rm BP}(f) = X_{\rm TP}(f)\star Z(f) = {1}/{2}\cdot X_{\rm | ||
TP} (f - f_{\rm T})+ {1}/{2}\cdot X_{\rm TP}(f + f_{\rm T}).$$ | TP} (f - f_{\rm T})+ {1}/{2}\cdot X_{\rm TP}(f + f_{\rm T}).$$ | ||
| − | + | Here it is considered that the [[Signal_Representation/The_Convolution_Theorem_and_Operation|Convolution]] of the spectral function $X_{\rm TP}(f)$ with the frequency-shifted Dirac signal $\delta (f - f_\rm {T})$ yields the same spectral function $X_{\rm TP}(f-f_\rm {T})$ shifted to the right by $f_\rm {T}$ . | |
[[File:P_ID2724__Sig_T_4_1_S4a.png|center|frame|Ein BP–Spektrum ergibt sich durch beidseitiges Verschieben eines TP–Spektrums]] | [[File:P_ID2724__Sig_T_4_1_S4a.png|center|frame|Ein BP–Spektrum ergibt sich durch beidseitiges Verschieben eines TP–Spektrums]] | ||
| − | + | From the right spectral range display you can clearly see that | |
| − | |||
:$$x_{\rm BP}(t) = x_{\rm TP}(t) \cdot {\cos} ( 2\pi \cdot f_{\rm T} | :$$x_{\rm BP}(t) = x_{\rm TP}(t) \cdot {\cos} ( 2\pi \cdot f_{\rm T} | ||
\cdot t)$$ | \cdot t)$$ | ||
| − | + | is a bandpass signal. The envelope of $x_{\rm BP}(t)$ given by the magnitude of $|x_{\rm TP}(t)|$ . | |
| − | + | For example, this principle is applied to the [[Modulation_Methods/Zweiseitenband-Amplitudenmodulation|amplitude modulation without carrier]],which is discussed thoroughly in the book „Modulation Methods”. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | You can see from the above graphic: | ||
| + | *The spectrum $X_{\rm BP}(f)$ has the same form as $f_{\rm T}$ in the range around the carrier frequency $f_{\rm TP}(f)$ in the range around $f = 0$, but is attenuated with respect to the low-pass spectrum by the factor $2$ . | ||
| + | *Since $X_{\rm TP}(f)$ relative to $f = 0$ has an even real and an odd imaginary part, the bandpass spectrum $X_{\rm BP}(f)$ has the same symmetry properties - but now relative to the carrier frequency $f_{\rm T}$. | ||
| + | *Also $X_{\rm BP}(f)$ has portions at negative frequencies. Since the corresponding signal $x_{\rm BP}(t)$ is also real according to the above equation, $X_{\rm BP}(f)$ must also have an even real and an odd imaginary part with respect to the frequency $f = 0$ . | ||
| + | *The bandwidth of the bandpass signal is twice that of the low-pass signal: $B_{\rm BP} = 2 \cdot B_{\rm TP}$. Prerequisite for the validity of this statement is that the carrier frequency $f_{\rm T}$ is at least larger than the maximum frequency $2$ by the factor $(B_{\rm TP})$ of the signal $x_{\rm TP}(t)$. | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ A low pass signal has discrete spectral components at $f_1 = 1\,\text{ kHz}, \,f_2 = 2\,\text{ kHz}, \,f_3 = 3\,\text{ kHz}$ and $f_4 = 4\,\text{ kHz}$: |
:$$x_{\rm TP}(t) = 0.26\cdot {\cos} ( \omega_1 \hspace{0.05cm} t + 20^{ \circ}) \hspace{0.18cm}+ 0.54\cdot {\cos} ( \omega_2 \hspace{0.05cm} t - 180^{ \circ}) + 0.30\cdot {\cos} ( \omega_3 \hspace{0.05cm} t + | :$$x_{\rm TP}(t) = 0.26\cdot {\cos} ( \omega_1 \hspace{0.05cm} t + 20^{ \circ}) \hspace{0.18cm}+ 0.54\cdot {\cos} ( \omega_2 \hspace{0.05cm} t - 180^{ \circ}) + 0.30\cdot {\cos} ( \omega_3 \hspace{0.05cm} t + | ||
| Line 168: | Line 167: | ||
\circ}).$$ | \circ}).$$ | ||
| − | + | The corresponding spectrum $X_{\rm TP}(f)$ is complex because of the non-zero phase positions. | |
| − | |||
| − | |||
| − | + | [[File:P_ID687__Sig_T_4_1_S4b.png|center|frame|DSB-AM-Signal With Different Carrier Frequencies]] | |
| − | |||
| − | |||
| + | *If one multiplies $x_{\rm TP}(t)$ with a cosine signal of amplitude $1$ and frequency $f_{\rm T} = 20 \,\text{kHz}$, the bandpass signal is obtained according to the upper graphic. | ||
| + | *The lower sketch applies to the bandpass signal with the carrier frequency $f_{\rm T} = 100 \,\text{kHz}$. | ||
| + | *In both illustrations the function curves $\pm \vert x_{\rm TP}(t) \vert $ can be recognized as the envelope of the bandpass signals. }} | ||
| − | |||
| − | + | ''Notes'': The topic of this chapter is covered in the german learning video [[Eigenschaften_von_Tiefpass-_und_Bandpasssignalen_(Lernvideo)|properties of bandpass and lowpass signals]] . | |
| − | |||
| − | |||
| + | Further information on the topic, numerous tasks and simulations can be found in the experiment „Analog Modulation Methods” of the practical course "Simulation of Digital Transmission Systems". This (former) LNT course at the TU Munich is based on | ||
| + | *dem Windows Program [http://en.lntwww.de/downloads/Sonstiges/Programme/AMV.zip AMV] ⇒ Link refers to the ZIP version of the program and | ||
| + | *the corresponding [http://en.lntwww.de/downloads/Sonstiges/Texte/Analoge_Modulationsverfahren.pdf Praktikumsanleitung] ⇒ Link refers to the PDF version; 86 pages in total. | ||
| − | == | + | ==Exercises for the Chapter== |
<br> | <br> | ||
| − | [[Aufgaben:Aufgabe_4.1:_Tiefpass-_und_Bandpass-Signale| | + | [[Aufgaben:Aufgabe_4.1:_Tiefpass-_und_Bandpass-Signale|Exercise 4.1: Tiefpass- und Bandpass-Signale]] |
[[Aufgaben:Aufgabe_4.1Z:_Hochpass-System|Aufgabe 4.1Z: Hochpass-System]] | [[Aufgaben:Aufgabe_4.1Z:_Hochpass-System|Aufgabe 4.1Z: Hochpass-System]] | ||
Revision as of 21:33, 24 November 2020
Contents
# OVERVIEW OF THE FOURTH MAIN CHAPTER #
In the third main chapter: Aperiodic Signals – Impulses often low-pass signals were assumed, i.e., those signals whose spectral functions lie in the range around the frequency $f = 0$ . Particularly in optical transmission and in radio transmission systems - but not only in these - the transmitted signals are in the range around a carrier frequency $f_{\rm T}$. Such signals are called bandpass signals.
All principles of the Fourier transformation and inverse transformation described in the last chapter apply to bandpass signals in the same way. Besides there are some special features of bandpass-signals, whose observance can lead to a simpler description.
This chapter contains in detail:
- the enumeration of differences and similarities of lowpass and bandpass signals,
- the synthesis of bandpass signals from the equivalent lowpass signal,
- the analytical signal and the corresponding spectral function,
- the equivalent low-pass signal in the time and frequency domain, and finally
- the representation of analytical signal/equivalent low-pass signal in the complex plane.
Further information about the topic as well as tasks, simulations and programming exercises can be found in the experiment Analog Modulation Methods of the practical course „Simulation of Digital Transmission Systems”. This (former) LNT course at the TU Munich is based on
- the Windows program AMV ⇒ Link refers to the zip version of the program
- and its lab manual ⇒ link refers to the pdf version (86 pages).
Motivation of Bandpass Signals for Communications Engineering
In the previous chapters of this book, almost only signals whose spectra lie in a narrow range around the frequency $f = 0$ have been considered. Examples are analog speech, music and image signals, which all - despite their different bandwidths - can be described as 'low pass signals .
If you want to transmit such a low-pass signal to a spatially distant sink, the signal may have to be converted to another frequency position. There can be several reasons for this:
- Often the transmission channel is unsuitable for the direct transmission of the source signal in the original frequency band, because this band contains frequencies that are unfavorable for it. Only by a frequency shift by means of a so-called modulator a transmission is made possible.
- A single transmission channel can be used for the simultaneous transmission of several signals, if they are modulated with different carrier frequencies at the transmitting end. This method is called FDMA ,abbreviated as Frequency Division Multiple Access
- The transmission quality can be improved compared to the simplest analog methodAmplitude Modulation at the expense of a larger bandwidth and thus a higher signal-to-noise ratio can be achieved. Examples are the. Frequency Modulation (FM) as an analog method and the digital Pul (PCM).
$\text{Remember:}$ The transmitted signals of many transmission methods are bandpass signals.
Note: Dem Autor ist durchaus bewusst, dass es nach der letzten Rechtschreibreform „Tiefpasssignal” und „Bandpasssignal” heißen müsste. Um diese unschönen Konstrukte zu vermeiden, verwenden wir im Folgenden meist die Schreibweisen „Tiefpass–Signal” und „Bandpass–Signal”, manchmal auch „TP–Signal” und „BP–Signal”.
$\text{Example 1 : To classify signals with respect to „low pass” and „bandpass”}$
(a) speech and music are low-pass signals with a bandwidth of $\text{20 kHz}$ (at very good quality). Since a radio transmission is only possible from approx. $\text{100 kHz}$ , a conversion to carrier frequencies between
- $\text{0.525 ... 1.61 MHz}$ $($Medium wave broadcasting, amplitude modulation, channel spacing $\text{9 kHz})$,
- $\text{87.5 ... 108 MHz}$ $($Radio on FM, frequency modulation, channel spacing $\text{300 kHz})$
is needed.
(b) TV image signals have a larger bandwidth, for example $\text{5 MHz}$ . Here, as well, a frequency band shift occurs before the sound and image transmission due to carrier frequencies between
- $\text{41 ... 68 / 174 ... 230 MHz}$ (television, VHF band, channel spacing $\text{7 MHz})$,
- $\text{470 ... 850 MHz}$ $($television, UHF band, channel spacing $\text{8 MHz})$.
(c) With GSM mobile radio the carrier frequencies in the D-band are $\text{900 MHz}$ and in the D-band $\text{1800 MHz}$.
(d) With optical transmission the electrical signals are converted into light, i.e. to frequencies between ca. $\text{200 THz}$ and $\text{350 THz}$ $($correspondingly $\text{1.55 µm ... 0.85 µm}$ Wavelength).
Properties of BP-Signals
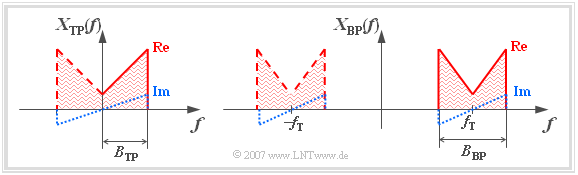
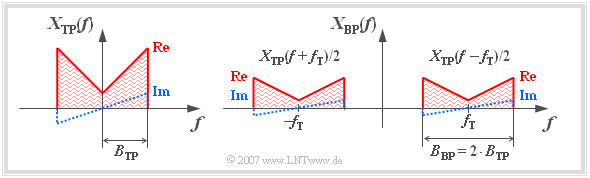
On this page - without claiming to be complete - some characteristics of bandpass signals are compiled and compared to lowpass signals. We start from the spectral functions $X_{\rm TP}(f)$ and $X_{\rm BP}(f)$ according to the following sketch.
Regarding the graphic is to be remarked:
- The triangular shape of the displayed spectra is to be understood schematically and is only to mark the occupied frequency band. So it should not be concluded that all frequencies within the band are actually occupied and that all spectral functions increase linearly with frequency $f$ .
- The corresponding time functions $x_{\rm TP}(t)$ and $x_{\rm BP}(t)$ are real for the time being. This means that according to the Mapping Theorem the spectral functions $X_{\rm TP}(f)$ and $X_{\rm BP}(f)$ - related to the frequency $f = 0$ - each have an even real part and an odd imaginary part.
- As bandwidth $B_{\rm TP}$ or. $B_{\rm BP}$ for both low pass and bandpass we refer to the occupied frequency band at the positive frequencies (in the graphic: continuous curves).
- As bandwidth $B_{\rm TP}$ or. $B_{\rm BP}$ for lowpass and bandpass we equally denote the occupied frequency band at the positive frequencies (in the graphic: continuous curves).
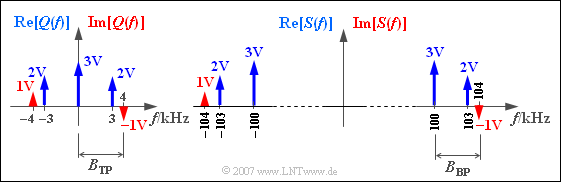
$\text{Example 2:}$ An example with discrete spectral lines follows. The left graph shows the spectrum $Q(f)$ of the message signal
- $$q(t) = 3\hspace{0.05cm}{\rm V} + 4\hspace{0.05cm}{\rm V} \cdot \cos (2 \pi \cdot 3\hspace{0.05cm}{\rm kHz} \cdot t) + 2\hspace{0.05cm}{\rm V} \cdot \sin (2 \pi \cdot 4\hspace{0.05cm}{\rm kHz} \cdot t). $$
The discrete spectral lines of the real part ⇒ ${\rm Re}\big[Q(f)\big]$ are shown in blue and those of the imaginary part ⇒ ${\rm Im}\big[Q(f)\big]$ in red.
On the right is the spectrum $S(f)$ after single sideband amplitude modulation (ESB-AM) with the carrier frequency $f_{\rm T} = 100 \,\text{kHz}$. A description of this transmission system can be found in chapter Envelope Demodulation of the book „Modulation Methods”.
- According to this description, $q(t)$ is uniquely a low-pass signal and $s(t)$ is a band-pass signal. The bandwidths are $B_{\rm TP} = B_{\rm BP} = 4 \,\text{kHz}$.
- If the DC component $(3 \,\text{V})$ would be missing in the source signal, then $q(t)$ would still be described as low-pass filter-like.
- Without knowledge of the task, one could interpret $q(t)$ but then also as a bandpass signal with the bandwidth $B_{\rm BP} = 1 \,\text{kHz}$ .
This example shows that there is no clear mathematical distinction between low pass and band pass signals.
Description of a BP-Signal with TP-Signals
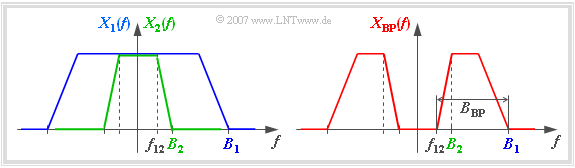
We consider two low pass spectra $X_1(f)$ and $X_2(f)$ with the bandwidths $B_1$ and $B_2$ corresponding to the left graph.
You can see from this diagram:
- If $X_1(f)$ and $X_2(f)$ up to a frequency $f_{12}$ are identical, the difference describes a bandpass spectrum with bandwidth $B_{\rm BP} = B_1 - f_{12}$. According to the graphic on the right, the following then applies
- $$X_{\rm BP}(f) = X_1(f) -X_2(f).$$
- Due to the linearity of the Fourier transform, the time function associated with the bandpass spectrum $X_{\rm BP}(f)$ is valid
- $$x_{\rm BP}(t) = x_1(t) - x_2(t).$$
- It generally follows from the Fourier transformation that the integral over the time function is equal to the spectral value at $f = 0$ . Consequently, this integral is always zero for every bandpass signal:
- $$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$
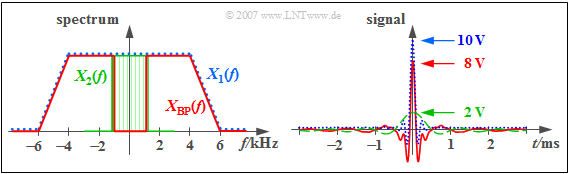
$\text{Example 3:}$ The red curves in the two graphs show the bandpass spectrum $X_{\rm BP}(f)$ and the corresponding time function
- $$x_{\rm BP}(t) = 10\hspace{0.05cm}{\rm V} \cdot {\rm si} ( \pi \cdot 10 \hspace{0.05cm}{\rm kHz} \cdot t) \cdot {\rm si} ( \pi \cdot 2 \hspace{0.05cm}{\rm kHz} \cdot t) - 2\hspace{0.05cm}{\rm V} \cdot {\rm si} ( \pi \cdot 2 \hspace{0.05cm}{\rm kHz} \cdot t).$$
Also shown are the two low-pass spectra and signals. You can see from these pictures:
- The blue-dotted curve in the left graph represents the trapezoidal spectrum $X_1(f)$ where the equivalent bandwidth $\Delta f_1= 10 \,\text{kHz}$ and the rolloff factor $r_1 = 0.2$ is
- The blue-dotted curve in the right graphic shows the corresponding low pass–signal $x_1(t)$. The signal value at $t = 0$ corresponds to the blue trapezoidal area of the spectrum $X_1(f)$:
- $$x_1(t = 0) = 10 \,\text{V}.$$
- The green curve applies to the rectangular spectrum $X_2(f)$ with the equivalent bandwidth $\Delta f_2= 2 \,\text{kHz}$. The corresponding time signal $x_2(t)$ runs $\sin(x)/x$-shaped and is valid:
- $$x_2(t = 0) = 2 \,\text{V}.$$
The red curve for the bandpass-like signal is the difference between the blue and green curve on the left and right. Accordingly
- $$x_{\rm BP}(t = 0) = x_1(t = 0) - x_2(t = 0) = 8 \,\text{V},$$
- $$\int_{- \infty}^{+\infty}x_{\rm BP}(t)\hspace{0.1cm}{\rm d}t = X_{\rm BP}(f \hspace{-0.1cm}= \hspace{-0.1cm} 0) =0.$$
BP-Signal Synthesis from Equivalent TP-Signals
We consider a low-pass signal $x_{\rm TP}(t)$ with spectrum $X_{\rm TP}(f)$ according to the left sketch.
If this signal is multiplied by a (dimensionless) harmonic oscillation
- $$z(t) = {\cos} ( 2\pi \cdot f_{\rm T} \cdot t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\hspace{0.15cm} Z(f) = {1}/{2}\cdot \delta (f - f_{\rm T})+ {1}/{2}\cdot \delta (f + f_{\rm T}),$$
the convolution theorem for the spectrum of the signal $x_{\rm BP}(t) = x_{\rm TP}(t) yields \cdot z(t)$:
- $$X_{\rm BP}(f) = X_{\rm TP}(f)\star Z(f) = {1}/{2}\cdot X_{\rm TP} (f - f_{\rm T})+ {1}/{2}\cdot X_{\rm TP}(f + f_{\rm T}).$$
Here it is considered that the Convolution of the spectral function $X_{\rm TP}(f)$ with the frequency-shifted Dirac signal $\delta (f - f_\rm {T})$ yields the same spectral function $X_{\rm TP}(f-f_\rm {T})$ shifted to the right by $f_\rm {T}$ .
From the right spectral range display you can clearly see that
- $$x_{\rm BP}(t) = x_{\rm TP}(t) \cdot {\cos} ( 2\pi \cdot f_{\rm T} \cdot t)$$
is a bandpass signal. The envelope of $x_{\rm BP}(t)$ given by the magnitude of $|x_{\rm TP}(t)|$ . For example, this principle is applied to the amplitude modulation without carrier,which is discussed thoroughly in the book „Modulation Methods”.
You can see from the above graphic:
- The spectrum $X_{\rm BP}(f)$ has the same form as $f_{\rm T}$ in the range around the carrier frequency $f_{\rm TP}(f)$ in the range around $f = 0$, but is attenuated with respect to the low-pass spectrum by the factor $2$ .
- Since $X_{\rm TP}(f)$ relative to $f = 0$ has an even real and an odd imaginary part, the bandpass spectrum $X_{\rm BP}(f)$ has the same symmetry properties - but now relative to the carrier frequency $f_{\rm T}$.
- Also $X_{\rm BP}(f)$ has portions at negative frequencies. Since the corresponding signal $x_{\rm BP}(t)$ is also real according to the above equation, $X_{\rm BP}(f)$ must also have an even real and an odd imaginary part with respect to the frequency $f = 0$ .
- The bandwidth of the bandpass signal is twice that of the low-pass signal: $B_{\rm BP} = 2 \cdot B_{\rm TP}$. Prerequisite for the validity of this statement is that the carrier frequency $f_{\rm T}$ is at least larger than the maximum frequency $2$ by the factor $(B_{\rm TP})$ of the signal $x_{\rm TP}(t)$.
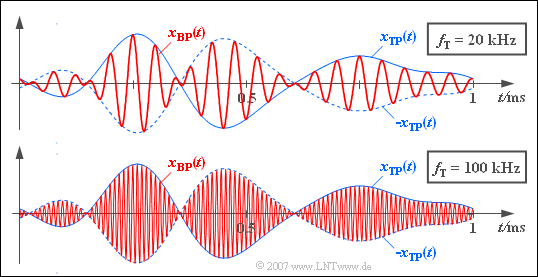
$\text{Example 4:}$ A low pass signal has discrete spectral components at $f_1 = 1\,\text{ kHz}, \,f_2 = 2\,\text{ kHz}, \,f_3 = 3\,\text{ kHz}$ and $f_4 = 4\,\text{ kHz}$:
- $$x_{\rm TP}(t) = 0.26\cdot {\cos} ( \omega_1 \hspace{0.05cm} t + 20^{ \circ}) \hspace{0.18cm}+ 0.54\cdot {\cos} ( \omega_2 \hspace{0.05cm} t - 180^{ \circ}) + 0.30\cdot {\cos} ( \omega_3 \hspace{0.05cm} t + 120^{ \circ}) +0.14\cdot {\cos} ( \omega_4 \hspace{0.05cm} t -40^{ \circ}).$$
The corresponding spectrum $X_{\rm TP}(f)$ is complex because of the non-zero phase positions.
- If one multiplies $x_{\rm TP}(t)$ with a cosine signal of amplitude $1$ and frequency $f_{\rm T} = 20 \,\text{kHz}$, the bandpass signal is obtained according to the upper graphic.
- The lower sketch applies to the bandpass signal with the carrier frequency $f_{\rm T} = 100 \,\text{kHz}$.
- In both illustrations the function curves $\pm \vert x_{\rm TP}(t) \vert $ can be recognized as the envelope of the bandpass signals.
Notes: The topic of this chapter is covered in the german learning video properties of bandpass and lowpass signals .
Further information on the topic, numerous tasks and simulations can be found in the experiment „Analog Modulation Methods” of the practical course "Simulation of Digital Transmission Systems". This (former) LNT course at the TU Munich is based on
- dem Windows Program AMV ⇒ Link refers to the ZIP version of the program and
- the corresponding Praktikumsanleitung ⇒ Link refers to the PDF version; 86 pages in total.
Exercises for the Chapter
Exercise 4.1: Tiefpass- und Bandpass-Signale
Aufgabe 4.2: Rechteckförmige Spektren
Aufgabe 4.2Z: Multiplikation mit Sinussignal