Difference between revisions of "Theory of Stochastic Signals/Cumulative Distribution Function"
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Kontinuierliche Zufallsgrößen |Vorherige Seite=Wahrscheinlichkeitsdichtefunktion (WDF) |Nächste Seite=Erwartungswerte und Momente }}…“) |
|||
| (67 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Continuous Random Variables |
| − | |Vorherige Seite= | + | |Vorherige Seite=Probability Density Function |
| − | |Nächste Seite= | + | |Nächste Seite=Expected Values and Moments |
}} | }} | ||
| − | == | + | ==Relationship between PDF and CDF== |
| − | + | <br> | |
| + | To describe random variables, in addition to the [[Theory_of_Stochastic_Signals/Probability_Density_Function|»probability density function»]] $\rm (PDF)$, we use the »cumulative distribution function« $\rm (CDF)$ which is defined as follows: | ||
| − | {{Definition} | + | {{BlaueBox|TEXT= |
| − | + | $\text{Definition:}$ The »'''cumulative distribution function'''« $F_{x}(r)$ corresponds to the probability that the random variable $x$ is less than or equal to a real number $r$: | |
| − | $$F_{ | + | :$$F_{x}(r) = {\rm Pr}( x \le r).$$}} |
| − | |||
| − | + | For a value-continuous random variable, the following statements are possible regarding the CDF: | |
| − | * | + | *The CDF is computable from the probability density function $f_{x}(x)$ by integration. It holds: |
| − | $$F_{ | + | :$$F_{x}(r) = \int_{-\infty}^{r}f_x(x)\,{\rm d}x.$$ |
| − | * | + | *Since the PDF is never negative, $F_{x}(r)$ increases at least weakly monotonically, and the function always lies between the following limits: |
| − | * | + | :$$F_{x}(r → \hspace{0.05cm} - \hspace{0.05cm} ∞) = 0, \hspace{0.5cm}F_{x}(r → +∞) = 1.$$ |
| − | $$f_{ | + | *Inversely, the probability density function can be determined from the CDF by differentiation: |
| − | : | + | :$$f_{x}(x)=\frac{{\rm d} F_{x}(r)}{{\rm d} r}\Bigg |_{\hspace{0.1cm}r=x}.$$ |
| + | :The addition »$r = x$« makes it clear that in our nomenclature the PDF argument is the random variable $x$ itself, while the CDF argument specifies any real variable $r$ . | ||
| − | + | {{BlaueBox|TEXT= | |
| − | $$F_{\rm | + | $\text{Notes on nomenclature:}$ If in the definitions of $\rm PDF$ and $\rm CDF$ we had distinguished |
| + | *between the random variable $X$ | ||
| + | |||
| + | *and the realizations $x ∈ X$ ⇒ $f_{X}(x), F_{X}(x)$, | ||
| + | |||
| + | |||
| + | we would have the following nomenclature: | ||
| + | :$$F_{X}(x) = {\rm Pr}(X \le x) = \int_{-\infty}^{x}f_{x}(\xi)\,{\rm d}\xi.$$ | ||
| + | |||
| + | Unfortunately, at the beginning of our $\rm LNTwww$ project $(2001)$ we decided to use our nomenclature for quite legitimate reasons, which now $(2017)$ cannot be changed, also with regard to the realized learning videos. '''So we stick with $f_{x}(x)$ instead of $f_{X}(x)$ as well as $F_{x}(r)$ instead of $F_{X}(x).$}} | ||
| + | |||
| + | ==CDF for value-continuous random variables== | ||
| + | <br> | ||
| + | The equations given in the last section apply only to value-continuous random variables and will be illustrated here by an example. In the next section it will be shown that for [[Theory_of_Stochastic_Signals/Cumulative_Distribution_Function#CDF_for_value-discrete_random_variables|»value-discrete random variables«]] the equations must be modified somewhat. | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 1:}$ The left image shows the photo »Lena«, which is often used as a test template for image coding procedures. | ||
| + | [[File:P_ID617__Sto_T_3_2_S1b_neu.png |right|frame| PDF and CDF of a value-continuous image]] | ||
| + | |||
| + | *If this image is divided into $256 × 256$ pixels, and the brightness is determined for each pixel, a sequence $〈x_ν〉$ of gray values is obtained whose length $N = 256^2 = 65\hspace{0.06cm}536$. | ||
| + | |||
| + | *The gray value $x$ is a value-continuous random variable, where the assignment to numerical values is arbitrary. For example, let »black« be characterized by $x = 0$ and »white« by $x = 1$: The value $x =0.5$ then characterizes a medium gray coloration. | ||
| + | |||
| + | |||
| + | The middle diagram shows the PDF $f_{x}(x)$ which is also often referred to in the literature as »gray value statistics«. | ||
| + | *In the original image some gray values are preferred and the two extreme values $x =0$ ("deep black") or $x =1$ ("pure white") occur very rarely. | ||
| + | |||
| + | *The cumulative distribution function $F_{x}(r)$ is continuous in value and increases monotonically from $0$ to $1$ as the right figure shows. | ||
| + | |||
| + | *For $r \approx 0$ and $r \approx 1$ the CDF is horizontal due to the lack of PDF components. | ||
| + | |||
| + | |||
| + | $\text{Note:}$ Strictly speaking, for an image that can be displayed on a computer $($in contrast to an analog photograph$)$: | ||
| + | # The gray value is always a discrete in value. | ||
| + | # However, with large resolution of the color information $($»color depth«$)$, this random variable can be approximated to be continuous in value. }} | ||
| + | |||
| + | |||
| + | » The topic of this chapter is illustrated with examples in the (German language) learning video <br> [[Zusammenhang_zwischen_WDF_und_VTF_(Lernvideo)|»Zusammenhang zwischen WDF und VTF»]] $\Rightarrow$ »Relationship between PDF and CDF«. | ||
| + | |||
| + | |||
| + | ==CDF for value-discrete random variables== | ||
| + | <br> | ||
| + | For the CDF calculation of a value-discrete random variable $x$ from its PDF, a more general equation must always be assumed. Here, with the auxiliary variable $\varepsilon > 0$: | ||
| + | :$$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm}0}\int_{-\infty}^{r+\varepsilon}f_x(x)\,{\rm d}x.$$ | ||
| + | |||
| + | *Due to the »less than/equal» sign in the [[Theory_of_Stochastic_Signals/Cumulative_Distribution_Function#Relationship_between_PDF_and_CDF|»general definition«]], a limit value must be formed for the CDF calculation. If we also take into account that, for a value-discrete random variable, the PDF consists of a sum of weighted [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal#Dirac_.28delta.29_function_in_frequency_domain|»Dirac delta functions«]], we obtain: | ||
| + | :$$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{r+\varepsilon}\sum\limits_{\mu= 1}^{ M}p_\mu\cdot \delta(x-x_\mu)\,{\rm d}x.$$ | ||
| + | *If we interchange integration and summation in this equation, and consider that an integration over the Dirac delta function yields the step function, we obtain: | ||
| + | :$$F_{x}(r)=\sum\limits_{\mu= \rm 1}^{\it M}p_\mu\cdot \gamma_0 (r-x_\mu),\hspace{0.4cm}{\rm with} \hspace{0.4cm}\gamma_0(x)=\lim_{\epsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{x+\varepsilon}\delta (u)\,{\rm d} u = \left\{ \begin{array}{*{2}{c}} 0 \hspace{0.4cm} {\rm if}\hspace{0.1cm} x< 0,\\ 1 \hspace{0.4cm} {\rm if}\hspace{0.1cm}x\ge 0. \\ \end{array} \right.$$ | ||
| + | ::The function $γ_0(x)$ differs from the [[Signal_Representation/Fourier_Transform_Theorems#Assignment_Theorem|»unit step function«]] $γ(x)$ often used in systems theory in that at the jump point $x = 0$ the right-hand side limit $1$nbsp; is valid $($instead of the mean value $0.5$ between left– and right–hand side limits$)$. | ||
| + | *With the above CDF definition, the following probability equation holds for value-continuous and value-discrete random variables equally, and of course also for mixed random variables with discrete and continuous parts: | ||
| + | :$${\rm Pr}(x_{\rm u}<x \le x_{\rm o})=F_x(x_{\rm o})-F_x(x_{\rm u}).$$ | ||
| + | *For purely value-continuous random variables, the »less than« sign and the »less than/equal to« sign could be substituted for each other here. | ||
| + | :$${\rm Pr}(x_{\rm u}<x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x < x_{\rm o}) ={\rm Pr}(x_{\rm u}<x < x_{\rm o}).$$ | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 2:}$ If the gray value of the [[Theory_of_Stochastic_Signals/Cumulative_Distribution_Function#CDF_for_continuous-valued_random_variables|»original Lena photo«]] is quantized by eight levels, so that each pixel can be represented by three bits and transmitted digitally, the discrete random variable $q$ is obtained. However, due to the quantization, a part of the image information is lost, which is reflected in the quantized image by clearly recognizable »contours«. | ||
| + | |||
| + | [[File:P_ID74__Sto_T_3_2_S2b_neu.png |right|frame| PDF and CDF of a value-discrete image]] | ||
| + | |||
| + | *The associated PDF $f_{q}(q)$ is composed of $M = 8$ Dirac delta functions, where, in the quantization chosen here, the possible gray levels are assigned the values $q_\mu = (\mu - 1)/7$ with $\mu = 1, 2,$ ... , $8$. | ||
| + | |||
| + | *The weights of the Dirac delta functions can be calculated from the PDF $f_{x}(x)$ of the original image. One obtains | ||
| + | :$$p_\mu={\rm Pr}(q = q_\mu ) = {\rm Pr}(\frac{2\mu-\rm 3}{14}< {x} \le\frac{2\it \mu- \rm 1}{14}) $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} p_\mu={\rm Pr}(q = q_\mu ) = \int_{(2\it \mu- \rm 3)/14}^{(2\mu-1)/14}\it f_{x}{\rm (}x{\rm )}\,{\rm d}x.$$ | ||
| + | *For the undefined areas $(x<0$, $x>1)$ is to be set $f_{x}(x) = 0$. Since in the original image the gray levels $x ≈0$ $($»very deep black«$)$ or $x ≈1$ $($»almost pure white«$)$ are largely missing, $p_1 ≈ p_8 ≈ 0$ result. | ||
| − | + | * Thus, only six Dirac delta functions are visible in the PDF. The two missing Diracs at $q = 0$ and $q =1$ are only indicated by dots. | |
| − | + | *The step-shaped CDF $F_{q}(r)$ sketched on the right thus has six points of discontinuity, where in each case the right-hand side limit is valid.}} | |
| + | |||
| + | » The topic of this chapter is illustrated with examples in the (German language) learning video <br> [[Zusammenhang_zwischen_WDF_und_VTF_(Lernvideo)|»Zusammenhang zwischen WDF und VTF»]] $\Rightarrow$ »Relationship between PDF and CDF«. | ||
| + | ==Exercises for the chapter== | ||
| + | <br> | ||
| + | [[Aufgaben:Exercise_3.2:_CDF_for_Exercise_3.1|Exercise 3.2: CDF for Exercise 3.1]] | ||
| + | [[Aufgaben:Exercise_3.2Z:_Relationship_between_PDF_and_CDF|Exercise 3.2Z: Relationship between PDF and CDF]] | ||
{{Display}} | {{Display}} | ||
Latest revision as of 17:47, 19 February 2024
Contents
Relationship between PDF and CDF
To describe random variables, in addition to the »probability density function» $\rm (PDF)$, we use the »cumulative distribution function« $\rm (CDF)$ which is defined as follows:
$\text{Definition:}$ The »cumulative distribution function« $F_{x}(r)$ corresponds to the probability that the random variable $x$ is less than or equal to a real number $r$:
- $$F_{x}(r) = {\rm Pr}( x \le r).$$
For a value-continuous random variable, the following statements are possible regarding the CDF:
- The CDF is computable from the probability density function $f_{x}(x)$ by integration. It holds:
- $$F_{x}(r) = \int_{-\infty}^{r}f_x(x)\,{\rm d}x.$$
- Since the PDF is never negative, $F_{x}(r)$ increases at least weakly monotonically, and the function always lies between the following limits:
- $$F_{x}(r → \hspace{0.05cm} - \hspace{0.05cm} ∞) = 0, \hspace{0.5cm}F_{x}(r → +∞) = 1.$$
- Inversely, the probability density function can be determined from the CDF by differentiation:
- $$f_{x}(x)=\frac{{\rm d} F_{x}(r)}{{\rm d} r}\Bigg |_{\hspace{0.1cm}r=x}.$$
- The addition »$r = x$« makes it clear that in our nomenclature the PDF argument is the random variable $x$ itself, while the CDF argument specifies any real variable $r$ .
$\text{Notes on nomenclature:}$ If in the definitions of $\rm PDF$ and $\rm CDF$ we had distinguished
- between the random variable $X$
- and the realizations $x ∈ X$ ⇒ $f_{X}(x), F_{X}(x)$,
we would have the following nomenclature:
- $$F_{X}(x) = {\rm Pr}(X \le x) = \int_{-\infty}^{x}f_{x}(\xi)\,{\rm d}\xi.$$
Unfortunately, at the beginning of our $\rm LNTwww$ project $(2001)$ we decided to use our nomenclature for quite legitimate reasons, which now $(2017)$ cannot be changed, also with regard to the realized learning videos. So we stick with $f_{x}(x)$ instead of $f_{X}(x)$ as well as $F_{x}(r)$ instead of $F_{X}(x).$
CDF for value-continuous random variables
The equations given in the last section apply only to value-continuous random variables and will be illustrated here by an example. In the next section it will be shown that for »value-discrete random variables« the equations must be modified somewhat.
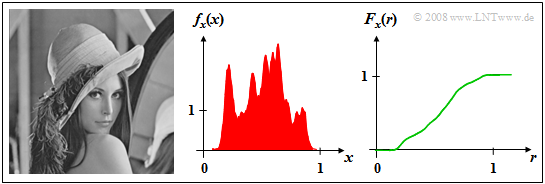
$\text{Example 1:}$ The left image shows the photo »Lena«, which is often used as a test template for image coding procedures.
- If this image is divided into $256 × 256$ pixels, and the brightness is determined for each pixel, a sequence $〈x_ν〉$ of gray values is obtained whose length $N = 256^2 = 65\hspace{0.06cm}536$.
- The gray value $x$ is a value-continuous random variable, where the assignment to numerical values is arbitrary. For example, let »black« be characterized by $x = 0$ and »white« by $x = 1$: The value $x =0.5$ then characterizes a medium gray coloration.
The middle diagram shows the PDF $f_{x}(x)$ which is also often referred to in the literature as »gray value statistics«.
- In the original image some gray values are preferred and the two extreme values $x =0$ ("deep black") or $x =1$ ("pure white") occur very rarely.
- The cumulative distribution function $F_{x}(r)$ is continuous in value and increases monotonically from $0$ to $1$ as the right figure shows.
- For $r \approx 0$ and $r \approx 1$ the CDF is horizontal due to the lack of PDF components.
$\text{Note:}$ Strictly speaking, for an image that can be displayed on a computer $($in contrast to an analog photograph$)$:
- The gray value is always a discrete in value.
- However, with large resolution of the color information $($»color depth«$)$, this random variable can be approximated to be continuous in value.
» The topic of this chapter is illustrated with examples in the (German language) learning video
»Zusammenhang zwischen WDF und VTF» $\Rightarrow$ »Relationship between PDF and CDF«.
CDF for value-discrete random variables
For the CDF calculation of a value-discrete random variable $x$ from its PDF, a more general equation must always be assumed. Here, with the auxiliary variable $\varepsilon > 0$:
- $$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm}0}\int_{-\infty}^{r+\varepsilon}f_x(x)\,{\rm d}x.$$
- Due to the »less than/equal» sign in the »general definition«, a limit value must be formed for the CDF calculation. If we also take into account that, for a value-discrete random variable, the PDF consists of a sum of weighted »Dirac delta functions«, we obtain:
- $$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{r+\varepsilon}\sum\limits_{\mu= 1}^{ M}p_\mu\cdot \delta(x-x_\mu)\,{\rm d}x.$$
- If we interchange integration and summation in this equation, and consider that an integration over the Dirac delta function yields the step function, we obtain:
- $$F_{x}(r)=\sum\limits_{\mu= \rm 1}^{\it M}p_\mu\cdot \gamma_0 (r-x_\mu),\hspace{0.4cm}{\rm with} \hspace{0.4cm}\gamma_0(x)=\lim_{\epsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{x+\varepsilon}\delta (u)\,{\rm d} u = \left\{ \begin{array}{*{2}{c}} 0 \hspace{0.4cm} {\rm if}\hspace{0.1cm} x< 0,\\ 1 \hspace{0.4cm} {\rm if}\hspace{0.1cm}x\ge 0. \\ \end{array} \right.$$
- The function $γ_0(x)$ differs from the »unit step function« $γ(x)$ often used in systems theory in that at the jump point $x = 0$ the right-hand side limit $1$nbsp; is valid $($instead of the mean value $0.5$ between left– and right–hand side limits$)$.
- With the above CDF definition, the following probability equation holds for value-continuous and value-discrete random variables equally, and of course also for mixed random variables with discrete and continuous parts:
- $${\rm Pr}(x_{\rm u}<x \le x_{\rm o})=F_x(x_{\rm o})-F_x(x_{\rm u}).$$
- For purely value-continuous random variables, the »less than« sign and the »less than/equal to« sign could be substituted for each other here.
- $${\rm Pr}(x_{\rm u}<x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x < x_{\rm o}) ={\rm Pr}(x_{\rm u}<x < x_{\rm o}).$$
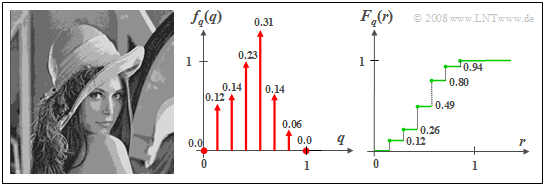
$\text{Example 2:}$ If the gray value of the »original Lena photo« is quantized by eight levels, so that each pixel can be represented by three bits and transmitted digitally, the discrete random variable $q$ is obtained. However, due to the quantization, a part of the image information is lost, which is reflected in the quantized image by clearly recognizable »contours«.
- The associated PDF $f_{q}(q)$ is composed of $M = 8$ Dirac delta functions, where, in the quantization chosen here, the possible gray levels are assigned the values $q_\mu = (\mu - 1)/7$ with $\mu = 1, 2,$ ... , $8$.
- The weights of the Dirac delta functions can be calculated from the PDF $f_{x}(x)$ of the original image. One obtains
- $$p_\mu={\rm Pr}(q = q_\mu ) = {\rm Pr}(\frac{2\mu-\rm 3}{14}< {x} \le\frac{2\it \mu- \rm 1}{14}) $$
- $$\Rightarrow \hspace{0.3cm} p_\mu={\rm Pr}(q = q_\mu ) = \int_{(2\it \mu- \rm 3)/14}^{(2\mu-1)/14}\it f_{x}{\rm (}x{\rm )}\,{\rm d}x.$$
- For the undefined areas $(x<0$, $x>1)$ is to be set $f_{x}(x) = 0$. Since in the original image the gray levels $x ≈0$ $($»very deep black«$)$ or $x ≈1$ $($»almost pure white«$)$ are largely missing, $p_1 ≈ p_8 ≈ 0$ result.
- Thus, only six Dirac delta functions are visible in the PDF. The two missing Diracs at $q = 0$ and $q =1$ are only indicated by dots.
- The step-shaped CDF $F_{q}(r)$ sketched on the right thus has six points of discontinuity, where in each case the right-hand side limit is valid.
» The topic of this chapter is illustrated with examples in the (German language) learning video
»Zusammenhang zwischen WDF und VTF» $\Rightarrow$ »Relationship between PDF and CDF«.
Exercises for the chapter
Exercise 3.2: CDF for Exercise 3.1
Exercise 3.2Z: Relationship between PDF and CDF