Difference between revisions of "Theory of Stochastic Signals/Generation of Discrete Random Variables"
| (51 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Discrete Random Variables |
| − | |Vorherige Seite= | + | |Vorherige Seite=Poisson Distribution |
|Nächste Seite=Wahrscheinlichkeitsdichtefunktion (WDF) | |Nächste Seite=Wahrscheinlichkeitsdichtefunktion (WDF) | ||
}} | }} | ||
| − | == | + | ==Pseudo-random variables== |
| − | + | <br> | |
| − | + | One way to generate a binary random sequence $〈z_{\rm ν}〉 ∈ \{0, 1\}$ with good statistical properties is offered by the so-called »'''pseudo-random generators'''«, also known as »'''PN generators'''«, where »PN« stands for »pseudo-noise«. | |
| − | |||
| − | |||
| + | These have the following properties: | ||
| + | #The binary sequence generated by such a generator is not stochastic in a strict sense, but exhibits periodic and thus deterministic properties. | ||
| + | #If the period length $P$ is sufficiently large, the sequence appears to an observer as random with sufficiently good statistical properties for many applications. | ||
| + | #The advantage of a pseudo-random generator over a real stochastic source is that the random sequence is reproducible if a few parameters are known. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 1:}$ The latter property also gives rise to the main applications of pseudo-noise generators, | ||
| + | # the »error rate measurement« in digital signal transmission, | ||
| + | # for »band spreading« in CDMA $($Code Division Multiple Access$)$. | ||
| − | |||
| − | + | In such a »Spread Spectrum System« the transmitted signal is modulated with a binary random sequence, whose symbol repetition frequency is significantly higher than the bit frequency. This offers the possibility of multiple channel utilization. Since the same sequence must be added in phase at the receiver, the use of reproducible pseudo-noise sequences is also common here. | |
| − | |||
| − | + | Detailed information on bandspreading methods can be found in the chapter [[Examples_of_Communication_Systems/General_Description_of_UMTS|»UMTS - Universal Mobile Telecommunications System«]] of the book »Examples of Communication Systems«.}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Realization of PN generators== | |
| + | <br> | ||
| + | Pseudo-random generators are usually realized by »feedback shift registers«, where at each clock instant the content of the register is shifted one place to the right $($see diagram$)$. For the currently generated symbol, with $g_l ∈ \{0, 1\}$ and $l = 1$, ... , $L-1$: | ||
| + | :$$z_\nu = (g_1\cdot z_{\nu-1}+g_2\cdot z_{\nu-2}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_l\cdot z_{\nu-l}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_{L-1}\cdot z_{\nu-L+1}+ z_{\nu-L})\hspace{0.1cm} \rm mod \hspace{0.2cm}2.$$ | ||
| − | [[File: | + | #The binary values $z_{ν-1}$ to $z_{ν-L}$ generated at previous time points are stored in the memory cells of the shift register. |
| + | #The coefficients $g_1$, ... , $g_{L-1}$ are also binary values, where $1$ indicates a feedback at the corresponding location and $0$ indicates no feedback. | ||
| + | #Modulo-2 addition can be implemented, for example, using an XOR operation: | ||
| + | [[File:EN_Sto_T_2_5_S2.png |right|frame| Pseudo-noise generator]] | ||
| + | :$$(x + y)\hspace{0.15cm} \rm mod\hspace{0.15cm}2 = \it x\hspace{0.15cm}\rm XOR\hspace{0.15cm} \it y = \left\{\begin{array}{*{2}{c}} \rm 0 & \rm if\hspace{0.15cm} \it x= y,\\ 1 & \rm if\hspace{0.15cm} \it x\neq y. \\ \end{array} \right.$$ | ||
| − | + | The statistical properties of the generated pseudo-noise random sequence $〈z_{\rm ν}〉$ are essentially determined by | |
| − | + | *the »'''degree'''« $L$, and | |
| − | |||
| − | |||
| − | * | ||
| + | *the »'''feedback coefficients'''« $g_{\hspace{0.05cm}l}$ $($with $l = 1$, ... , $L-1)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | A prerequisite for the generation of a pseudo-noise sequence is that not all memory elements are preallocated with zeros, otherwise the modulo-2 addition would always generate the symbol $0$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | To identify different pseudo-noise generators one uses in the literature alternatively: | |
| − | + | *The »'''generator polynomial'''« | |
| − | + | :$$G(D) = g_L\cdot D^L+g_{L-1}\cdot D^{L-1}+ \ \text{...} \ +g_1\cdot D+g_0 .$$ | |
| − | + | :Here, $g_0 = g_L = 1$ is always to be set; $D$ is a formal parameter indicating a delay by one clock $(D^L$ indicates a delay by $L$ clocks$)$. | |
| + | |||
| + | *The »'''octal representation'''« of the binary number $(g_L\ \text{ ...} \ g_2 \ g_1 \ g_0)$. <br>It is important that the feedback coefficients – starting from the right with $g_0$ – are combined into triples and these are written octal $(0 \ \text{...}\ 7)$. | ||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 2:}$ | ||
| + | The generator polynomial $D^4 + D^3 + 1$ belongs to a shift register of degree $L = 4$ with the following octal representation. | ||
| + | :$$(g_4 \ g_3 \ g_2 \ g_1 \ g_0) = (11\hspace{0.05cm} 001)_{\rm bin} = (31)_{\rm oct}. $$}} | ||
| − | [[File: | + | ==Sequences of maximum length (M-sequences)== |
| + | <br> | ||
| + | If not all $L$ memory cells of the shift register are preallocated with zeros, a periodic random sequence $〈z_ν\rangle$ always results: | ||
| + | [[File:EN_Sto_T_2_5_S5_neu.png|right|frame|Composition of some favorable generator polynomials]] | ||
| + | *The period length $P$ of the pseudo-noise sequence depends to a strong degree on the feedback coefficients. | ||
| + | *For each degree $L$ there is at least one configuration with »'''maximum period length'''« | ||
| + | :$$P_{\rm max} = \rm 2^{\it L}-\rm 1.$$ | ||
| + | *Such a pseudo-noise sequence is also often referred to as »'''M-sequence'''«, where the »$\rm M$« stands for »maximum«. | ||
| + | <br><br> | ||
| + | The table lists pseudo-noise generators of maximum length up to degree $L = 31$. | ||
| + | <u>Note:</u> | ||
| + | #The selection is limited to configurations with only one tap $($two returns$)$. | ||
| + | #This means that the associated polynomials consist of only three summands. | ||
| + | #For applications that require high speed, such generators are very useful. | ||
| + | <br clear=all> | ||
| + | {{BlueBox|TEXT= | ||
| + | $\text{For now without proof:}$ | ||
| + | |||
| + | $(1)$ An »'''M-sequence'''« can be recognized by the fact that the generator polynomial $G(D)$ is »'''primitive'''«. | ||
| − | + | $(2)$ As detailed in the book [[Channel_Coding|»Channel Coding«]], a polynomial $G(D)$ of degree $L$ is called »primitive« if the following condition is satisfied: | |
| + | ::$${\rm For}\hspace{0.2cm}\it n<P_{\rm max} \rm = \rm 2^{\it L}-\rm 1\text{:}\hspace{0.5cm}\frac{D^n+ 1}{G(D)} \neq 0. $$}} | ||
| + | <br clear=all> | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 3:}$ A shift register of degree $L = 4$ with octal identifier $(31)$ and generator polynomial $G(D) = D^4 + D^3 + 1$ leads to a sequence of maximum length: | ||
| + | :$$P_{\rm max} = 2^4 - 1 = 15.$$ | ||
| + | The mathematical proof for this equation is rathercomplex: | ||
| + | #Using the above polynomial division for $n = 1$, ... , $14$ one must show that the quotient is always non–zero. | ||
| + | #First the division $(D^{15} + 1)/G(D)$ may give a result without remainder. | ||
| + | #Here it is to be considered that in the modulo-2 algebra $+1$ and $-1$ are identical. }} | ||
| − | == | + | ==Reciprocal polynomials== |
| − | {{Definition} | + | <br> |
| − | + | {{BlueBox|TEXT= | |
| − | $$G_{\rm R}(D)=D^{L}\cdot G(D^{-1}).$$ | + | $\text{Definition:}$ |
| − | + | The »'''reciprocal polynomial'''« associated with the generator polynomial $G(D)$ is: | |
| + | :$$G_{\rm R}(D)=D^{L}\cdot G(D^{-1}).$$}} | ||
| − | + | There are the following relations between the two shift registers with polynomials $G(D)$ resp. $G_{\rm R}(D)$: | |
| − | + | #If $G(D)$ provides a sequence of maximum length ⇒ $P_{\rm max} = 2^L - 1$, then the period length of the reciprocal polynomial $G_{\rm R}(D)$ is also maximum. | |
| − | + | #The output sequences of reciprocal configurations are »inverses of each other«. That is:<br> The sequence of $G(D)$ – read from right to left – gives the sequence of the reciprocal configuration $G_{\rm R}(D)$. | |
| − | In | + | In the [[Theory_of_Stochastic_Signals/Generation_of_Discrete_Random_Variables#Sequences_of_maximum_length_.28M-sequences.29 |$\text{table above}$]] the reciprocal polynomials $G_{\rm R}(D)$ associated to $G(D)$ are given in the third column up to register degree $L = 31$ . |
| − | {{ | + | {{GraueBox|TEXT= |
| − | + | $\text{Example 4:}$ | |
| − | $$ | + | We consider again a pseudo-noise generator with degree $L = 4$ and shift register structure $(31)_{\rm oct}$ : |
| + | :$$G(D) = 1+D^{3} + D^{4}.$$ | ||
| − | + | * For the reciprocal polynomial we obtain the configuration with the octal identifier $(23)$: | |
| − | * ... $0 \ 0 | + | :$$G_{\rm R}(D) = D^{\rm 4}\cdot (1+D^{-3} + D^{ -4})=D^{ 4}+D^{1}+\rm 1.$$ |
| − | * ... $0 | + | |
| + | *The corresponding output sequences each have the maximum period length $P_{\rm max} = 15$ and are inverses of each other: | ||
| + | :* ... $0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 1$ ... | ||
| + | :* ... $0 \ 1 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 1 \ 1 \ 1 \ 1$ ... | ||
| + | *This means that the upper initial sequence of $(31)$, read from right to left, yields the sequence of reciprocal order $(23)$ given below. | ||
| − | + | *However, a cyclic phase shift of four binary digits can be seen. }} | |
| − | |||
| − | + | ==Generation of multi-level random variables== | |
| + | <br> | ||
| + | Many high-level programming languages provide pseudo-random generators that return real random numbers $x$ equally distributed between $0$ and $1$. For example, a corresponding C–function call is: | ||
| − | + | :$$x = \text{random()}.$$ | |
| − | + | By successively calling this random function, a periodically repeating sequence of real numbers is created, where all values $0 \le x < 1$ are equally likely <br>(see chapter [[Theory_of_Stochastic_Signals/Uniformly_Distributed_Random_Variables|»Uniformly Distributed Random Variables»$)$]]. | |
| − | + | #However, since the period $P$ is very large, this sequence can be considered as »pseudo-random«. | |
| + | #By specifying a starting value, the pseudo-random sequence is started at certain points. | ||
| − | |||
| − | + | When generating a discrete-value multilevel random variable $z$ it is convenient to assume such a uniformly distributed random variable $x$. | |
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 5:}$ | ||
| + | The graphic shows the principle for the special case $M = 3$ ⇒ ternary random sequence $〈z_{\rm ν}〉$ with $z_{\rm ν} ∈ \{0,\ 1,\ 2\}$. | ||
| + | [[File:P_ID457__Sto_T_2_5_S6neu.png|right|frame|For generating multi-level random variables]] | ||
| + | *Assumed is the between $0$ and $1$ uniformly distributed random variable $x$. | ||
| + | |||
| + | *The desired probabilities are designated as follows: | ||
| + | :$$p_0 = {\rm Pr}(z_{\rm ν} =0),\hspace{0.5cm} p_1 = {\rm Pr}(z_{\rm ν} =1),\hspace{0.5cm} p_2 = {\rm Pr}(z_{\rm ν} =2). $$ | ||
| − | {{ | + | Then holds: |
| − | + | #If the current $x_{\rm ν} <p_0$, then the ternary random variable is set to $z_{\rm ν} = 0$. | |
| + | #In the range $p_0 ≤ x_{\rm ν} < p_0 + p_1$ the output is $z_{\rm ν} = 1$ . | ||
| + | #For $x_{\rm ν} \ge p_0 + p_1$ the ternary random variable becomes $z_{\rm ν} =2$. | ||
| − | |||
| − | |||
| − | |||
| − | + | In the listed C–program, | |
| + | *we get for $M = 3$ and for the current random value $x = 0.57$ | ||
| + | *the product $x · M = 0.57 · 3 = 1.71$ and thus the ternary random variable $z = 1$. | ||
| − | + | *For an other random value $x = 0.95$ on the other hand, the function would return the result $z = 2$. | |
| − | |||
| − | |||
| − | |||
| − | + | For reasons of comprehension, a cumbersome programming was chosen here. The given C–program part could also be written more compactly: | |
| − | + | :$$\text{\{ float random(); return((long) (random()*M)); \} }$$}} | |
| − | |||
| − | [[Aufgaben: | + | ==Exercises for the chapter== |
| + | <br> | ||
| + | [[Aufgaben:Exercise_2.6:_PN_Generator_of_Length_5|Exercise 2.6: PN Generator of Length 5]] | ||
| − | [[Aufgaben:2. | + | [[Exercise_2.6Z:_PN_Generator_of_Length_3|Exercise 2.6Z: PN Generator of Length 3]] |
| + | |||
| + | [[Aufgaben:Exercise_2.7:_C_Programs_"z1"_and_"z2"|Exercise 2.7: C Programs "z1" and "z2"]] | ||
| + | |||
| + | [[Aufgaben:Exercise_2.7Z:_C_Program_"z3"|Exercise 2.7Z: C Program "z3"]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Display}} | {{Display}} | ||
Latest revision as of 19:39, 8 February 2024
Contents
Pseudo-random variables
One way to generate a binary random sequence $〈z_{\rm ν}〉 ∈ \{0, 1\}$ with good statistical properties is offered by the so-called »pseudo-random generators«, also known as »PN generators«, where »PN« stands for »pseudo-noise«.
These have the following properties:
- The binary sequence generated by such a generator is not stochastic in a strict sense, but exhibits periodic and thus deterministic properties.
- If the period length $P$ is sufficiently large, the sequence appears to an observer as random with sufficiently good statistical properties for many applications.
- The advantage of a pseudo-random generator over a real stochastic source is that the random sequence is reproducible if a few parameters are known.
$\text{Example 1:}$ The latter property also gives rise to the main applications of pseudo-noise generators,
- the »error rate measurement« in digital signal transmission,
- for »band spreading« in CDMA $($Code Division Multiple Access$)$.
In such a »Spread Spectrum System« the transmitted signal is modulated with a binary random sequence, whose symbol repetition frequency is significantly higher than the bit frequency. This offers the possibility of multiple channel utilization. Since the same sequence must be added in phase at the receiver, the use of reproducible pseudo-noise sequences is also common here.
Detailed information on bandspreading methods can be found in the chapter »UMTS - Universal Mobile Telecommunications System« of the book »Examples of Communication Systems«.
Realization of PN generators
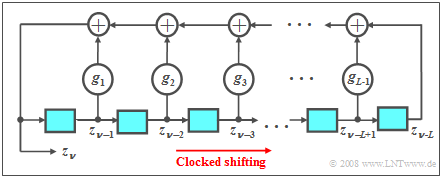
Pseudo-random generators are usually realized by »feedback shift registers«, where at each clock instant the content of the register is shifted one place to the right $($see diagram$)$. For the currently generated symbol, with $g_l ∈ \{0, 1\}$ and $l = 1$, ... , $L-1$:
- $$z_\nu = (g_1\cdot z_{\nu-1}+g_2\cdot z_{\nu-2}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_l\cdot z_{\nu-l}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_{L-1}\cdot z_{\nu-L+1}+ z_{\nu-L})\hspace{0.1cm} \rm mod \hspace{0.2cm}2.$$
- The binary values $z_{ν-1}$ to $z_{ν-L}$ generated at previous time points are stored in the memory cells of the shift register.
- The coefficients $g_1$, ... , $g_{L-1}$ are also binary values, where $1$ indicates a feedback at the corresponding location and $0$ indicates no feedback.
- Modulo-2 addition can be implemented, for example, using an XOR operation:
- $$(x + y)\hspace{0.15cm} \rm mod\hspace{0.15cm}2 = \it x\hspace{0.15cm}\rm XOR\hspace{0.15cm} \it y = \left\{\begin{array}{*{2}{c}} \rm 0 & \rm if\hspace{0.15cm} \it x= y,\\ 1 & \rm if\hspace{0.15cm} \it x\neq y. \\ \end{array} \right.$$
The statistical properties of the generated pseudo-noise random sequence $〈z_{\rm ν}〉$ are essentially determined by
- the »degree« $L$, and
- the »feedback coefficients« $g_{\hspace{0.05cm}l}$ $($with $l = 1$, ... , $L-1)$.
A prerequisite for the generation of a pseudo-noise sequence is that not all memory elements are preallocated with zeros, otherwise the modulo-2 addition would always generate the symbol $0$.
To identify different pseudo-noise generators one uses in the literature alternatively:
- The »generator polynomial«
- $$G(D) = g_L\cdot D^L+g_{L-1}\cdot D^{L-1}+ \ \text{...} \ +g_1\cdot D+g_0 .$$
- Here, $g_0 = g_L = 1$ is always to be set; $D$ is a formal parameter indicating a delay by one clock $(D^L$ indicates a delay by $L$ clocks$)$.
- The »octal representation« of the binary number $(g_L\ \text{ ...} \ g_2 \ g_1 \ g_0)$.
It is important that the feedback coefficients – starting from the right with $g_0$ – are combined into triples and these are written octal $(0 \ \text{...}\ 7)$.
$\text{Example 2:}$ The generator polynomial $D^4 + D^3 + 1$ belongs to a shift register of degree $L = 4$ with the following octal representation.
- $$(g_4 \ g_3 \ g_2 \ g_1 \ g_0) = (11\hspace{0.05cm} 001)_{\rm bin} = (31)_{\rm oct}. $$
Sequences of maximum length (M-sequences)
If not all $L$ memory cells of the shift register are preallocated with zeros, a periodic random sequence $〈z_ν\rangle$ always results:
- The period length $P$ of the pseudo-noise sequence depends to a strong degree on the feedback coefficients.
- For each degree $L$ there is at least one configuration with »maximum period length«
- $$P_{\rm max} = \rm 2^{\it L}-\rm 1.$$
- Such a pseudo-noise sequence is also often referred to as »M-sequence«, where the »$\rm M$« stands for »maximum«.
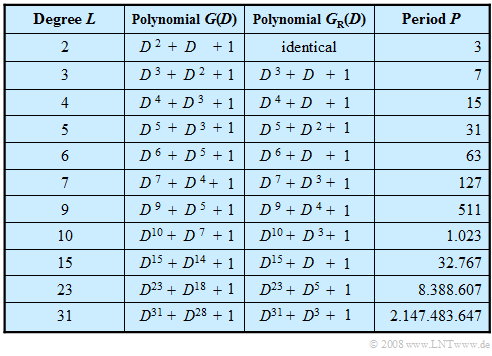
The table lists pseudo-noise generators of maximum length up to degree $L = 31$.
Note:
- The selection is limited to configurations with only one tap $($two returns$)$.
- This means that the associated polynomials consist of only three summands.
- For applications that require high speed, such generators are very useful.
$\text{For now without proof:}$
$(1)$ An »M-sequence« can be recognized by the fact that the generator polynomial $G(D)$ is »primitive«.
$(2)$ As detailed in the book »Channel Coding«, a polynomial $G(D)$ of degree $L$ is called »primitive« if the following condition is satisfied:
- $${\rm For}\hspace{0.2cm}\it n<P_{\rm max} \rm = \rm 2^{\it L}-\rm 1\text{:}\hspace{0.5cm}\frac{D^n+ 1}{G(D)} \neq 0. $$
$\text{Example 3:}$ A shift register of degree $L = 4$ with octal identifier $(31)$ and generator polynomial $G(D) = D^4 + D^3 + 1$ leads to a sequence of maximum length:
- $$P_{\rm max} = 2^4 - 1 = 15.$$
The mathematical proof for this equation is rathercomplex:
- Using the above polynomial division for $n = 1$, ... , $14$ one must show that the quotient is always non–zero.
- First the division $(D^{15} + 1)/G(D)$ may give a result without remainder.
- Here it is to be considered that in the modulo-2 algebra $+1$ and $-1$ are identical.
Reciprocal polynomials
$\text{Definition:}$ The »reciprocal polynomial« associated with the generator polynomial $G(D)$ is:
- $$G_{\rm R}(D)=D^{L}\cdot G(D^{-1}).$$
There are the following relations between the two shift registers with polynomials $G(D)$ resp. $G_{\rm R}(D)$:
- If $G(D)$ provides a sequence of maximum length ⇒ $P_{\rm max} = 2^L - 1$, then the period length of the reciprocal polynomial $G_{\rm R}(D)$ is also maximum.
- The output sequences of reciprocal configurations are »inverses of each other«. That is:
The sequence of $G(D)$ – read from right to left – gives the sequence of the reciprocal configuration $G_{\rm R}(D)$.
In the $\text{table above}$ the reciprocal polynomials $G_{\rm R}(D)$ associated to $G(D)$ are given in the third column up to register degree $L = 31$ .
$\text{Example 4:}$ We consider again a pseudo-noise generator with degree $L = 4$ and shift register structure $(31)_{\rm oct}$ :
- $$G(D) = 1+D^{3} + D^{4}.$$
- For the reciprocal polynomial we obtain the configuration with the octal identifier $(23)$:
- $$G_{\rm R}(D) = D^{\rm 4}\cdot (1+D^{-3} + D^{ -4})=D^{ 4}+D^{1}+\rm 1.$$
- The corresponding output sequences each have the maximum period length $P_{\rm max} = 15$ and are inverses of each other:
- ... $0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 1$ ...
- ... $0 \ 1 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 1 \ 1 \ 1 \ 1$ ...
- This means that the upper initial sequence of $(31)$, read from right to left, yields the sequence of reciprocal order $(23)$ given below.
- However, a cyclic phase shift of four binary digits can be seen.
Generation of multi-level random variables
Many high-level programming languages provide pseudo-random generators that return real random numbers $x$ equally distributed between $0$ and $1$. For example, a corresponding C–function call is:
- $$x = \text{random()}.$$
By successively calling this random function, a periodically repeating sequence of real numbers is created, where all values $0 \le x < 1$ are equally likely
(see chapter »Uniformly Distributed Random Variables»$)$.
- However, since the period $P$ is very large, this sequence can be considered as »pseudo-random«.
- By specifying a starting value, the pseudo-random sequence is started at certain points.
When generating a discrete-value multilevel random variable $z$ it is convenient to assume such a uniformly distributed random variable $x$.
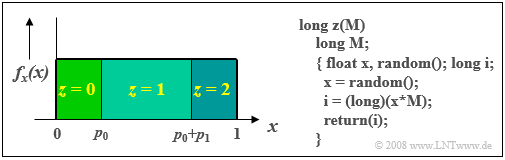
$\text{Example 5:}$ The graphic shows the principle for the special case $M = 3$ ⇒ ternary random sequence $〈z_{\rm ν}〉$ with $z_{\rm ν} ∈ \{0,\ 1,\ 2\}$.
- Assumed is the between $0$ and $1$ uniformly distributed random variable $x$.
- The desired probabilities are designated as follows:
- $$p_0 = {\rm Pr}(z_{\rm ν} =0),\hspace{0.5cm} p_1 = {\rm Pr}(z_{\rm ν} =1),\hspace{0.5cm} p_2 = {\rm Pr}(z_{\rm ν} =2). $$
Then holds:
- If the current $x_{\rm ν} <p_0$, then the ternary random variable is set to $z_{\rm ν} = 0$.
- In the range $p_0 ≤ x_{\rm ν} < p_0 + p_1$ the output is $z_{\rm ν} = 1$ .
- For $x_{\rm ν} \ge p_0 + p_1$ the ternary random variable becomes $z_{\rm ν} =2$.
In the listed C–program,
- we get for $M = 3$ and for the current random value $x = 0.57$
- the product $x · M = 0.57 · 3 = 1.71$ and thus the ternary random variable $z = 1$.
- For an other random value $x = 0.95$ on the other hand, the function would return the result $z = 2$.
For reasons of comprehension, a cumbersome programming was chosen here. The given C–program part could also be written more compactly:
- $$\text{\{ float random(); return((long) (random()*M)); \} }$$
Exercises for the chapter
Exercise 2.6: PN Generator of Length 5
Exercise 2.6Z: PN Generator of Length 3
Exercise 2.7: C Programs "z1" and "z2"