Difference between revisions of "Theory of Stochastic Signals/Moments of a Discrete Random Variable"
| Line 36: | Line 36: | ||
==Quadratischer Mittelwert – Varianz – Streuung== | ==Quadratischer Mittelwert – Varianz – Streuung== | ||
Analog zum linearen Mittelwert erhält man mit $k =$ 2 für den quadratischen Mittelwert: | Analog zum linearen Mittelwert erhält man mit $k =$ 2 für den quadratischen Mittelwert: | ||
| + | $$m_2 =\sum_{\mu=\rm 1}^{\it M}p_\mu\cdot z_\mu^2 =\lim_{N\to\infty}\frac{\rm 1}{\it N}\sum_{\nu=\rm 1}^{\it N}z_\nu^2.$$ | ||
| + | Bei Nachrichtensignalen gibt $m_2$ die (mittlere) ''Leistung'' an, bezogen auf den Widerstand 1 Ω. Beschreibt $z$ eine Spannung, so besitzt $m_2$ die Einheit $„{\rm V}^2”$. Zusammen mit dem Gleichanteil $m_1$ kann daraus als weitere Kenngröße die Varianz $σ^2$ bestimmt werden (''Satz von Steiner''): | ||
| + | $$\sigma^2=m_2-m_1^2.$$ | ||
| + | Als Streuung $σ$ bezeichnet man in der Statistik die Quadratwurzel der Varianz; manchmal wird diese Größe auch ''Standardabweichung'' genannt. | ||
| + | Die Varianz $σ^2$ eines Zufallssignals entspricht physikalisch der ''Wechselleistung'' und die Streuung $σ$ dem ''Effektivwert.'' Dieser Definition liegt wiederum der Bezugswiderstand 1 Ω zugrunde. | ||
| + | Nachfolgendes Lernvideo verdeutlicht die definierten Größen am Beispiel eines Digitalsignals: | ||
| + | Bedeutung und Berechnung der Momente bei diskreten Zufallsgrößen (Dauer 6:30) | ||
| + | {{Beispiel}} | ||
| + | Ein Binärsignal mit den Amplitudenwerten 1 V (Symbol '''L''') und 3 V (Symbol '''H''') sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} =$ 0.2 bzw. $p_{\rm H} =$ 0.8 hat eine Signalleistung von 7.4 ${\rm V}^2$. Mit $m_1 =$ 2.6 V (siehe vorherige Seite) folgt daraus $σ^2 =$ 0.64 ${\rm V}^2$ bzw. $σ =$ 0.8 V. | ||
| + | ''Hinweis:'' Bei anderem Bezugswiderstand ⇒ $R ≠$ 1 Ω gelten obige Bezeichnungen nur bedingt. Beispielsweise haben die Leistung $P$, die Wechselleistung $P_{\rm W}$ und der Effektivwert $s_{\rm eff}$ mit $R =$ 50 Ω folgende Werte: | ||
| + | $$P \hspace{-0.05cm}= \hspace{-0.05cm} \frac{m_2}{R} \hspace{-0.05cm}= \hspace{-0.05cm} \frac{7.4\,{\rm V}^2}{50\,{\rm \Omega}} \hspace{-0.05cm}= \hspace{-0.05cm}0.148\,{\rm W},\hspace{0.15cm} | ||
| + | P_{\rm W} \hspace{-0.05cm} = \hspace{-0.05cm} \frac{\sigma^2}{R} \hspace{-0.05cm}= \hspace{-0.05cm}12.8\,{\rm mW} \hspace{0.05cm},\hspace{0.15cm} | ||
| + | s_{\rm eff} \hspace{-0.05cm} = \hspace{-0.05cm}\sqrt{R \cdot P_{\rm W}} \hspace{-0.05cm}= \hspace{-0.05cm} \sigma \hspace{-0.05cm}= \hspace{-0.05cm} 0.8\,{\rm V}.$$ | ||
| + | [[File:P_ID456__Sto_T_2_2_S3_neu.png | Standardabweichung eines Binärsignals]] | ||
| + | |||
| + | Die gleiche Varianz und der gleiche Effektivwert ergeben sich für die Amplitudenwerte 0 V (für das Symbol '''L''') und 2 V (für das Symbol '''H'''), vorausgesetzt, die Auftrittswahrscheinlichkeiten $p_{\rm L} =$ 0.2 und $p_{\rm H} =$ 0.8 bleiben gleich. Dagegen stimmen die Momente – zum Beispiel der lineare Mittelwert $m_1$ und der quadratische Mittelwert $m_2$ – dann nicht mehr überein. | ||
| + | {{end}} | ||
{{Display}} | {{Display}} | ||
Revision as of 23:48, 25 May 2016
Berechnung als Schar- bzw. Zeitmittelwert
Die Wahrscheinlichkeiten bzw. die relativen Häufigkeiten liefern weitreichende Informationen über eine diskrete Zufallsgröße. Reduzierte Informationen erhält man durch die so genannten Momente $m_k$, wobei $k$ eine natürliche Zahl darstellt.
Unter der hier stillschweigend vorausgesetzten Ergodizität gibt es für das Moment $k$-ter Ordnung zwei unterschiedliche Berechnungsmöglichkeiten:
- die Scharmittelung bzw. Erwartungswertbildung (Mittelung über alle möglichen Werte):
$$m_k = \rm E \it [z^k] = \sum_{\mu = \rm 1}^{\it M}p_\mu \cdot z_\mu^k \hspace{2cm} \rm mit \hspace{0.1cm} {\rm E[...]:} \hspace{0.1cm} \rm Erwartungswert ,$$
- die Zeitmittelung über die Zufallsfolge 〈 $z_ν$〉 mit der Laufvariablen $ν =$ 1 , ... , $N$:
$$m_k=\overline{z_\nu^k}=\hspace{0.01cm}\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=\rm 1}^{\it N}z_\nu^k\hspace{1.7cm}\rm mit\hspace{0.1cm}\ddot{u}berstreichender\hspace{0.1cm}Linie:\hspace{0.1cm}Zeitmittelwert.$$
Beide Berechnungsarten führen für genügend große Werte von $N$ zum gleichen asymptotischen Ergebnis. Bei endlichem $N$ ergibt sich ein vergleichbarer Fehler, als wenn die Wahrscheinlichkeit durch die relative Häufigkeit angenähert wird.
Linearer Mittelwert - Gleichanteil
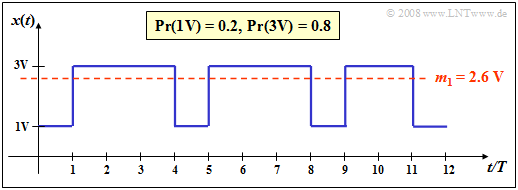
Mit $k =$ 1 erhält man aus der allgemeinen Gleichung für die Momente den linearen Mittelwert: $$m_1 =\sum_{\mu=1}^{M}p_\mu\cdot z_\mu =\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=1}^{N}z_\nu.$$ Der linke Teil dieser Gleichung beschreibt die Scharmittelung (über alle möglichen Werte), während die rechte Gleichung die Bestimmung als Zeitmittelwert angibt. In Zusammenhang mit Signalen wird diese Größe auch als der Gleichanteil bezeichnet.
Ein Binärsignal mit den beiden Amplitudenwerten 1V (für das Symbol L) und 3V (für das Symbol H) sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} =$ 0.2 bzw. $p_{\rm H} =$ 0.8 besitzt den linearen Mittelwert $$m_1 = 0.2 \cdot 1\,{\rm V}+ 0.8 \cdot 3\,{\rm V}= 2.6 \,{\rm V}. $$ Dieser Gleichanteil ist in der Grafik als rote Linie eingezeichnet.
Bestimmt man diese Kenngröße durch Zeitmittelung über die dargestellten $N =$ 12 Signalwerte, so wird man einen etwas kleineren Wert erhalten: $$m_1' = 1/3 \cdot 1\,{\rm V}+ 2/3 \cdot 3\,{\rm V}= 2.33 \,{\rm V}. $$ Hier wurden die Auftrittswahrscheinlichkeiten $p_{\rm L} =$ 0.2 bzw. $p_{\rm H} =$ 0.8 durch die entsprechenden Häufigkeiten $h_{\rm L} =$ 4/12 und $h_{\rm H} =$ 8/12 ersetzt. Der relative Fehler aufgrund der unzureichenden Folgenlänge $N$ ist im Beispiel größer als 10%.
Quadratischer Mittelwert – Varianz – Streuung
Analog zum linearen Mittelwert erhält man mit $k =$ 2 für den quadratischen Mittelwert: $$m_2 =\sum_{\mu=\rm 1}^{\it M}p_\mu\cdot z_\mu^2 =\lim_{N\to\infty}\frac{\rm 1}{\it N}\sum_{\nu=\rm 1}^{\it N}z_\nu^2.$$
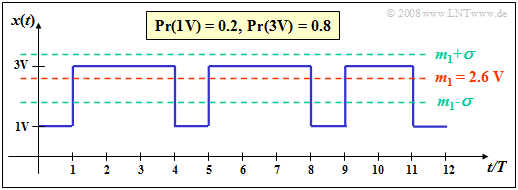
Bei Nachrichtensignalen gibt $m_2$ die (mittlere) Leistung an, bezogen auf den Widerstand 1 Ω. Beschreibt $z$ eine Spannung, so besitzt $m_2$ die Einheit $„{\rm V}^2”$. Zusammen mit dem Gleichanteil $m_1$ kann daraus als weitere Kenngröße die Varianz $σ^2$ bestimmt werden (Satz von Steiner): $$\sigma^2=m_2-m_1^2.$$ Als Streuung $σ$ bezeichnet man in der Statistik die Quadratwurzel der Varianz; manchmal wird diese Größe auch Standardabweichung genannt.
Die Varianz $σ^2$ eines Zufallssignals entspricht physikalisch der Wechselleistung und die Streuung $σ$ dem Effektivwert. Dieser Definition liegt wiederum der Bezugswiderstand 1 Ω zugrunde.
Nachfolgendes Lernvideo verdeutlicht die definierten Größen am Beispiel eines Digitalsignals:
Bedeutung und Berechnung der Momente bei diskreten Zufallsgrößen (Dauer 6:30)
Ein Binärsignal mit den Amplitudenwerten 1 V (Symbol L) und 3 V (Symbol H) sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} =$ 0.2 bzw. $p_{\rm H} =$ 0.8 hat eine Signalleistung von 7.4 ${\rm V}^2$. Mit $m_1 =$ 2.6 V (siehe vorherige Seite) folgt daraus $σ^2 =$ 0.64 ${\rm V}^2$ bzw. $σ =$ 0.8 V.
Hinweis: Bei anderem Bezugswiderstand ⇒ $R ≠$ 1 Ω gelten obige Bezeichnungen nur bedingt. Beispielsweise haben die Leistung $P$, die Wechselleistung $P_{\rm W}$ und der Effektivwert $s_{\rm eff}$ mit $R =$ 50 Ω folgende Werte: $$P \hspace{-0.05cm}= \hspace{-0.05cm} \frac{m_2}{R} \hspace{-0.05cm}= \hspace{-0.05cm} \frac{7.4\,{\rm V}^2}{50\,{\rm \Omega}} \hspace{-0.05cm}= \hspace{-0.05cm}0.148\,{\rm W},\hspace{0.15cm} P_{\rm W} \hspace{-0.05cm} = \hspace{-0.05cm} \frac{\sigma^2}{R} \hspace{-0.05cm}= \hspace{-0.05cm}12.8\,{\rm mW} \hspace{0.05cm},\hspace{0.15cm} s_{\rm eff} \hspace{-0.05cm} = \hspace{-0.05cm}\sqrt{R \cdot P_{\rm W}} \hspace{-0.05cm}= \hspace{-0.05cm} \sigma \hspace{-0.05cm}= \hspace{-0.05cm} 0.8\,{\rm V}.$$
Die gleiche Varianz und der gleiche Effektivwert ergeben sich für die Amplitudenwerte 0 V (für das Symbol L) und 2 V (für das Symbol H), vorausgesetzt, die Auftrittswahrscheinlichkeiten $p_{\rm L} =$ 0.2 und $p_{\rm H} =$ 0.8 bleiben gleich. Dagegen stimmen die Momente – zum Beispiel der lineare Mittelwert $m_1$ und der quadratische Mittelwert $m_2$ – dann nicht mehr überein.