Set Theory Basics

Venn Diagram, Universe and Empty Set

Set representation in the Venn diagram

In later chapters, we will sometimes refer to set theory . Therefore, the most important basics and definitions of this discipline will be briefly summarized here. The topic is also covered in the learning video set theory terms and regularities using the example of European countries.

An important tool of set theory is the Venn diagramm according to the graph:

Applied to probability theory, here the events $A_i$ are represented as areas. For a simpler description we do not denote the events here with $A_1$, $A_2$ and $A_3$, but with $A$, $B$ and $C$ in contrast to the last chapter. he total area corresponds to the universe $G$.
The universe $G$ contains all possible outcomes and stands for the certain event, which by definition occurs with probability „one”: ${\rm Pr}(G) = 1$. For example, in the random experiment "throwing a die", the probability for the event "the number of eyes is less than or equal to 6" is identical to one.
In contrast, the empty set $ϕ$ does not contain a single element. In terms of events, the empty set specifies the impossible event with probability ${\rm Pr}(ϕ) = 0$ an. For example, in the experiment "throwing a die"' the probability for the event "the number of eyes is greater than 6" is identically zero.

Note that not every event $A$ with ${\rm Pr}(A) = 0$ can really never occur:

For example, although the probability of the event "the noise value $n$ is identically zero" is vanishingly small and ${\rm Pr}(n \equiv 0) = 0$, if $n$ is described by a continuous (Gaussian) random variable.
Nevertheless, it is of course possible (although extremely unlikely) that at some point the exact noise value $n = 0$ will also occur.

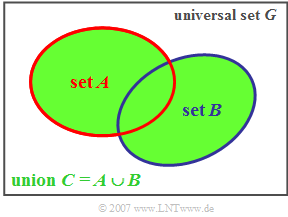
Set Union

On the basis of the Venn diagram some set-theoretical connections are explained now.

$\text{Definition:}$ The set union $C$ of two sets $A$ and $B$ contains all the elements that are contained either in set $A$ or in set $B$ or in set. This relationship is expressed as the following formula: $$\ C = A \cup B \hspace{0.2cm}(= A + B).$$

!!!!!!!!!!!!!!! In der Literatur ist auch die Bezeichnung Summenmenge gebräuchlich und es wird manchmal das Pluszeichen benutzt. In unserem Tutorial verwenden wir jedoch ausschließlich das $∪$-Zeichen.

!!!!!!!!!!!!!!!

Set Union in the Venn Diagram

Using the diagram, it is easy to see the following laws of set theory:

$$A \cup \it \phi = A \rm \hspace{3.6cm}(Union \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}empty \hspace{0.15cm}set),$$

$$A\cup G = G \rm \hspace{3.6cm}(Union \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}universe),$$

$$A\cup A = A \hspace{3.6cm}(\rm Tautology),$$

$$A\cup B = B\cup A \hspace{2.75cm}(\rm Commutative property),$$

$$(A\cup B)\cup C = A\cup (B\cup C) \hspace{0.45cm}(\rm Associative property).$$

If nothing else is known about the event sets $A$ and $B$ then only a lower bound and an upper bound can be given for the probability of the set union:

$${\rm Max}\big({\rm Pr} (A), \ {\rm Pr} (B)\big) \le {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B).$$

The probability of the set union is equal to the lower bound if $A$ is a subset of $B$ or vice versa.
The upper bound holds for disjoint sets.

$\text{Example 1:}$ Consider the two events

$A :=$ „the number is greater than or equal to $5$”$ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$,
$B :=$ „the number is even” $= \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$,

then the set union contains four elements: $(A \cup B) = \{2, 4, 5, 6 \}$ ⇒ ${\rm Pr} (A \cup B) = 4/6 = 2/3$.

The lower bound is given by ${\rm Pr} (A \cup B) \ge {\rm Max}\big({\rm Pr} (A),\ {\rm Pr} (B)\big ) = 3/6.$
For the upper bound $ {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B) = 5/6.$

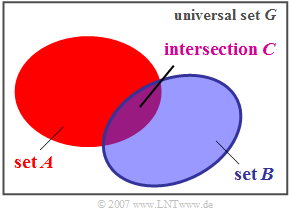
Intersection

Eine weitere wichtige mengentheoretische Verknüpfung stellt die Schnittmenge dar.

$\text{Definition:}$ Die Schnittmenge $C$ zweier Mengen $A$ und $B$ beinhaltet alle diejenigen Elemente, die sowohl in der Menge $A$ als auch in der Menge $B$ enthalten sind (englisch: Intersecting Set ). Formelmäßig wird dieser Zusammenhang wie folgt ausgedrückt:

$$C = A \cap B \hspace{0.2cm}(= A \cdot B).$$

In der Literatur ist hierfür auch die Bezeichnung Produktmenge gebräuchlich und man verwendet teilweise das Multiplikationssymbol.

Schnittmenge im Venndiagramm

In der Grafik ist die Schnittmenge violett dargestellt. Analog zur Vereinigungsmenge sind hier folgende Gesetzmäßigkeiten zu nennen:

$$A \cap \it \phi = \it \phi \rm \hspace{3.75cm}(Schnitt \hspace{0.15cm}mit \hspace{0.15cm}der \hspace{0.15cm}leeren \hspace{0.15cm}Menge),$$

$$A \cap G = A \rm \hspace{3.6cm}(Schnitt \hspace{0.15cm}mit \hspace{0.15cm}der \hspace{0.15cm}Grundmenge),$$

$$A\cap A = A \rm \hspace{3.6cm}(Tautologiegesetz),$$

$$A\cap B = B\cap A \rm \hspace{2.75cm}(Kommutativgesetz),$$

$$(A\cap B)\cap C = A\cap (B\cap C) \rm \hspace{0.45cm}(Assoziativgesetz).$$

Ist über $A$ und $B$ nichts weiter bekannt, so kann für die Wahrscheinlichkeit der Schnittmenge keine Aussage getroffen werden.
Gilt jedoch ${\rm Pr} (A) \le 1/2$ und gleichzeitig ${\rm Pr} (B) \le 1/2$, so kann eine untere und eine obere Schranke angegeben werden:

$$0 \le {\rm Pr} (A ∩ B) \le {\rm Min}\ \big({\rm Pr} (A),\ {\rm Pr} (B)\big ).$$

${\rm Pr}(A ∩ B)$ wird manchmal auch "Verbundwahrscheinlichkeit" genannt und mit ${\rm Pr}(A, \ B)$ bezeichnet.
${\rm Pr}(A ∩ B)$ ist gleich der oberen Schranke, wenn $A$ eine Teilmenge von $B$ ist oder umgekehrt.
Die untere Schranke ergibt sich für die Verbundwahrscheinlichkeit von disjunkten Mengen.

$\text{Beispiel 2:}$ Wir betrachten wieder die beiden Ereignisse

$A :=$ „die Augenzahl ist größer oder gleich $5$”$ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$, und
$B :=$ „die Augenzahl ist geradzahlig”$ = \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$,

Die Schnittmenge beinhaltet nur ein einziges Element: $(A ∩ B) = \{ 6 \}$ ⇒ ${\rm Pr} (A ∩ B) = 1/6$.

Die obere Schranke ergibt sich zu ${\rm Pr} (A ∩ B) \le {\rm Min}\ \big ({\rm Pr} (A), \, {\rm Pr} (B)\big ) = 2/6.$
Die untere Schranke der Schnittmenge ist hier wegen ${\rm Pr} (A) \le 1/2$ und ${\rm Pr} (B) \le 1/2$ gleich Null.

Komplementärmenge

$\text{Definition:}$ Die Komplementärmenge (englisch: Complementary Set) von $A$ wird oft durch eine überstreichende Linie $(\overline{A})$ gekennzeichnet. Sie beinhaltet alle die Elemente, die in der Menge $A$ nicht enthalten sind, und es gilt für deren Wahrscheinlichkeit:

$${\rm Pr}(\overline{A}) = 1- {\rm Pr}(A).$$

Komplementärmenge im Venndiagramm

Im dargestellten Venndiagramm ist die zu $A$ komplementäre Menge schraffiert dargestellt. Aus diesem Schaubild sind einige mengentheoretische Beziehungen zu erkennen:

Die Komplementärmenge der komplementären Menge von $A$ ist die Menge $A$ selbst:

$$\overline{\overline{A}} = A.$$

Die Vereinigungsmenge einer Menge $A$ mit ihrer Komplentärmenge ergibt die Grundmenge:

$${\rm Pr}(A \cup \overline{A}) = {\rm Pr}(G) = \rm 1.$$

Die Schnittmenge von $A$ mit ihrer Komplementärmenge ergibt die leere Menge:

$${\rm Pr}(A \cap \overline{A}) = {\rm Pr}({\it \phi}) \rm = 0.$$

$\text{Beispiel 3:}$ Ausgehend von der Menge

$A :=$ „die Augenzahl ist kleiner als $5$” $= \{1, 2, 3, 4\}$ ⇒ ${\rm Pr} (A)= 2/3$

lautet die zugehörige Komplentärmenge:

$\overline{A} :=$ „die Augenzahl ist größer oder gleich $5$”$ = \{5, 6\}$ ⇒ ${\rm Pr} (\overline{A})= 1 - {\rm Pr} (A) = 1 - 2/3 = 1/3.$

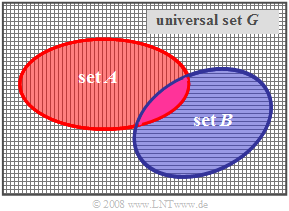
Echte Teilmenge – Unechte Teilmenge

Teilmengen im Venndiagramm

$\text{Definitionen:}$ Man nennt $A$ eine echte Teilmenge von $B$ (englisch: Strict Subset) und schreibt hierfür $A ⊂ B$,

wenn alle Elemente von $A$ auch in $B$ enthalten sind,
aber nicht gleichzeitig alle Elemente von $B$ auch in $A$.

In diesem Fall gilt für die Wahrscheinlichkeiten:

$${\rm Pr}(A) < {\rm Pr}(B).$$

Diese mengentheoretische Relation wird durch das skizzierte Venndiagramm veranschaulicht.

Dagegen bezeichnet man $A$ als eine unechte Teilmenge von $B$ und verwendet die Notation

$$A \subseteq B = (A \subset B) \cup (A = B),$$

wenn $A$ entweder eine echte Teilmenge von $B$ ist oder wenn $A$ und $B$ gleiche Mengen sind.

Für die Wahrscheinlichkeiten gilt dann die Größenrelation ${\rm Pr} (A) \le {\rm Pr} (B)$.
Das Gleichheitszeichen gilt nur für den Sonderfall $A = B$.

Daneben gelten aber auch die beiden als Absorptionsgesetze bekannten Gleichungen:

$$(A \cap B) \cup A = A ,$$

$$(A \cup B) \cap A = A,$$

da die Schnittmenge $A ∩ B$ stets eine Teilmenge von $A$ ist, aber gleichzeitig auch $A$ eine Teilmenge der Vereinigungsmenge $A ∪ B$ ist.

$\text{Beispiel 4:}$ Wir betrachten bei unserem Standardexperiment "Werfen eines Würfels" ⇒ $G = \{1, 2, 3, 4, 5, 6\}$ nun die beiden Ereignisse

$A :=$ „die Augenzahl ist ungerade”$ = \{1, 3, 5\}$ ⇒ ${\rm Pr} (A)= 3/6$, und
$B :=$ „die Augenzahl ist eine Primzahl” $= \{1, 2, 3, 5\}$ ⇒ ${\rm Pr} (B)= 4/6$.

Man erkennt, dass $A$ eine (echte) Teilmenge der Menge $B$ ist. Dementsprechend gilt auch ${\rm Pr} (A) < {\rm Pr} (B).$

Theoreme von de Morgan

rechts

Bei vielen Aufgaben aus der Mengenlehre sind die beiden Theoreme von de Morgan äußerst nützlich. Diese lauten:

$$\overline{A \cup B} = \overline{A} \cap \overline{B},$$

$$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$

Diese Gesetzmäßigkeiten sind im Schaubild veranschaulicht:

Die Menge $A$ ist rot dargestellt und die Menge $B$ blau.
Die Komplentärmenge $\overline {A}$ von $A$ ist in horizontaler Richtung schraffiert.
Die Komplentärmenge $\overline {B}$ von $B$ ist in vertikaler Richtung schraffiert.
Das Komplement $\overline{A \cup B}$ der Vereinigungsmenge ${A \cup B}$ ist sowohl horizontal als auch vertikal schraffiert.
Es ist damit gleich der Schnittmenge $\overline{A} \cap \overline{B}$ der beiden Komplentärmengen von $A$ und $B$:

$$\overline{A \cup B} = \overline{A} \cap \overline{B}.$$

Auch die zweite Form des de Morgan-Theorems lässt sich mit diesem Venndiagramm grafisch verdeutlichen:

Die Schnittmenge $A ∩ B$ (im Bild violett dargestellt) ist weder horizontal noch vertikal schraffiert.
Das Komplement $\overline{A ∩ B}$ der Schnittmenge ist dementsprechend entweder horizontal, vertikal oder in beiden Richtungen schraffiert.
Nach dem zweiten Theorem von de Morgan ist das Komplement der Schnittmenge gleich der Vereinigungsmenge der beiden Komplentärmengen von $A$ und $B$:

$$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$

$\text{Beispiel 5:}$ Wir betrachten die beiden Mengen

$A : =$ „die Augenzahl ist ungeradzahlig” $= \{1, 3, 5\}$,
$B : =$ „die Augenzahl ist größer als $2$” $= \{3, 4, 5, 6\}$.

Daraus folgen die beiden komplementären Mengen

$\overline {A} : =$ „die Augenzahl ist geradzahlig” $= \{2, 4, 6\}$,
$\overline {B} : =$ „die Augenzahl ist kleiner als $3$” $= \{1, 2\}$.

Weiter erhält man mit den obigen Theoremen die folgenden Teilmengen:

$$\overline{A \cup B} = \overline{A} \cap \overline{B} = \{2\}\hspace{0.5 cm}\rm und \hspace{0.5cm} \overline{\it A \cap \it B} =\overline{\it A} \cup \overline{\it B} = \{1,2,4,6\}.$$

Disjunkte Mengen

$\text{Definition:}$ Zwei Mengen $A$ und $B$ nennt man disjunkt (englisch: disjoint) oder miteinander unvereinbar,

wenn es kein einziges Element gibt,
das sowohl in $A$ als auch in $B$ enthalten ist.

rechts

Das Schaubild zeigt zwei disjunkte Mengen $A$ und $B$ im Venndiagramm.

In diesem Sonderfall gelten die folgenden Aussagen:

Die Schnittmenge zweier disjunkter Mengen $A$ und $B$ ergibt stets die leere Menge:

$${\rm Pr}(A \cap B) = {\rm Pr}(\phi) = \rm 0.$$

Die Wahrscheinlichkeit der Vereinigungsmenge zweier disjunkter Mengen $A$ und $B$ ist immer gleich der Summe der beiden Einzelwahrscheinlichkeiten:

$${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B).$$

$\text{Beispiel 6:}$ Bei unserem Standardexperiment sind die beiden Mengen

$A :=$ „die Augenzahl ist kleiner als $3$”$ = \{1, 2\}$ ⇒ ${\rm Pr}( A) = 2/6$, und
$B :=$ „die Augenzahl ist größer als $3$” $ = \{4, 5,6\}$ ⇒ ${\rm Pr}( B) = 3/6$

zueinander disjunkt, da $A$ und $B$ kein einziges gemeinsames Element beinhalten.

Die Schnittmenge ergibt die leere Menge: ${A \cap B} = \phi$.
Die Wahrscheinlichkeit der Vereinigungsmenge ${A \cup B} = \{1, 2, 4, 5, 6\}$ ist gleich ${\rm Pr}( A) + {\rm Pr}(B) = 5/6.$

Additionstheorem

Nur bei disjunkten Mengen $A$ und $B$ gilt für die Wahrscheinlichkeit der Vereinigungsmenge der Zusammenhang ${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B)$. Wie errechnet sich diese Wahrscheinlichkeit aber bei allgemeinen, nicht notwendigerweise disjunkten Ereignissen?

Zum Additionstheorem der Wahrscheinlichkeitsrechnung

Betrachten Sie das rechte Venndiagramm mit der violett dargestellten Schnittmenge $A ∩ B$.

Die rote Menge beinhaltet alle Elemente, die zu $A$ gehören, aber nicht zu $B$.
Die Elemente von $B$, die nicht gleichzeitig in $A$ enthalten sind, sind blau dargestellt.
Alle roten, blauen und violetten Flächen zusammen ergeben die Vereinigungsmenge $A ∪ B$.

Aus dieser mengentheoretischen Darstellung erkennt man folgende Zusammenhänge:

$${\rm Pr}(A) \hspace{0.8cm}= {\rm Pr}(A \cap B) + {\rm Pr}(A \cap \overline{B}),$$

$${\rm Pr}(B) \hspace{0.8cm}= {\rm Pr}(A \cap B) \rm +{\rm Pr}(\overline{A} \cap {B}),$$

$${\rm Pr}(A \cup B) ={\rm Pr}(A \cap B) +{\rm Pr} ({A} \cap \overline{B}) \rm + {\rm Pr}(\overline{A} \cap {B}).$$

Addiert man die ersten beiden Gleichungen und subtrahiert davon die dritte, so erhält man:

$${\rm Pr}(A) \rm +{\rm Pr}(B) -{\rm Pr}(A \cup B) = {\rm Pr}(A \cap B).$$

$\text{Definition:}$ Durch Umstellen dieser Gleichung kommt man zum sogenannten Additionstheorem (englisch: Addition Rule) für zwei beliebige, nicht notwendigerweise disjunkte Ereignisse:

$${\rm Pr}(A \cup B) = {\rm Pr}(A) + {\rm Pr}(B) - {\rm Pr}(A \cap B).$$

$\text{Beispiel 7:}$ Wir betrachten die beiden Mengen

$A :=$ „die Augenzahl ist ungeradzahlig” $= \{1, 3, 5\}$ ⇒ ${\rm Pr}(A) = 3/6$, und
$B :=$ „die Augenzahl ist größer als $2$”$ = \{3, 4, 5, 6\}$ ⇒ ${\rm Pr}(B) = 4/6$.

Damit ergeben sich für die Wahrscheinlichkeiten

der Vereinigungsmenge ⇒ ${\rm Pr}(A ∪ B) = 5/6$, und
der Schnittmenge ⇒ ${\rm Pr}(A ∩ B) = 2/6$.

Die Zahlenwerte zeigen die Gültigkeit des Additionstheorems: $5/6 = 3/6 + 4/6 − 2/6$.

Vollständiges System

Im letzten Abschnitt zu diesem Kapitel betrachten wir wieder mehr als zwei mögliche Ereignisse, nämlich allgemein $I$. Diese Ereignisse werden im Folgenden mit $A_i$ bezeichnet, und es gilt für den Laufindex: $1 ≤ i ≤ I$.

$\text{Definition:}$ Eine Konstellation mit den Ereignissen $A_1, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_i, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_I$ bezeichnet man dann und nur dann als ein vollständiges System, wenn die beiden folgenden Bedingungen erfüllt sind:

(1) Alle Ereignisse sind paarweise disjunkt:

$$A_i \cap A_j = \it \phi \hspace{0.15cm}\rm f\ddot{u}r\hspace{0.15cm}alle\hspace{0.15cm}\it i \ne j.$$

(2) Die Vereinigung aller Ereignismengen ergibt die Grundmenge:

$$\bigcup_{i=1}^{I} A_i = G.$$

Aufgrund dieser beiden Voraussetzungen gilt dann für die Summe aller Wahrscheinlichkeiten:

$$\sum_{i =1}^{ I} {\rm Pr}(A_i) = 1.$$

$\text{Beispiel 8:}$ Die Ereignismengen $A_1 := \{1, 5\}$ und $A_2 := \{2, 3\}$ ergeben beim Zufallsexperiment "Werfen eines Würfels" zusammen mit der Menge $A_3 := \{4, 6\}$ ein vollständiges System, nicht jedoch beim Experiment "Werfen einer Roulettekugel".

$\text{Beispiel 9:}$ Ein weiteres Beispiel für ein vollständiges System ist die diskrete Zufallsgröße $X = \{ x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ mit den Auftrittswahrscheinlichkeiten entsprechend der folgenden Wahrscheinlichkeitsfunktion:

$$P_X(X) = \big [ \hspace{0.1cm} P_X(x_1), P_X(x_2), \hspace{0.05cm}\text{...}\hspace{0.15cm}, P_X(x_I) \hspace{0.05cm} \big ] = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_I \hspace{0.05cm} \big ] \hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm} p_1 = P_X(x_1) = {\rm Pr}(X=x_1) \hspace{0.05cm}, \hspace{0.2cm}p_2 = {\rm Pr}(X=x_2) \hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.15cm},\hspace{0.2cm} p_I = {\rm Pr}(X=x_I) \hspace{0.05cm}.$$

Die möglichen Ergebnisse $x_i$ der Zufallsgröße $X$ sind paarweise zueinander disjunkt und die Summe aller Auftrittswahrscheinlichkeiten $p_1 + p_2 + \hspace{0.1cm}\text{...}\hspace{0.1cm} + \hspace{0.05cm} p_I$ liefert grundsätzlich das Ergebnis $1$.

$\text{Beispiel 10:}$ Es gelte $X= \{0, 1, 2 \}$ und $P_X (X) = \big[0.2, \ 0.5, \ 0.3\big]$. Dann gilt:

$${\rm Pr}(X=0) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=1) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=2) = 0.3 \hspace{0.05cm}.$$

Bei der Zufallsgröße $X = \{1, \pi, {\rm e} \}$ und gleichem $P_X(X) = \big[0.2, \ 0.5, \ 0.3\big]$ lauten die Zuordnungen:

$${\rm Pr}(X=1) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=\pi) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X={\rm e}) = 0.3 \hspace{0.05cm}.$$

Hinweise:

Die Wahrscheinlichkeitsfunktion $P_X(X)$ macht nur Aussagen über die Wahrscheinlichkeiten, nicht über den Wertevorrat $\{x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ der Zufallsgröße $X$.
Diese zusätzliche Information liefert die Wahrscheinlichkeitsdichtefunktion (WDF).