Examples of Communication Systems/Telecommunications Aspects of UMTS

1. Examples of Communication Systems
2. UMTS – Universal Mobile Telecommunications System
3. Telecommunications Aspects of UMTS

• Previous page
• Next page

• Previous page
• Next page

Verbesserungen bezüglich Sprachcodierung

Im Kapitel  GSM  (Global System for Mobile Communications)  dieses Buches wurden bereits mehrere Sprachcodecs ausführlich beschrieben:

$\text{Zur Erinnerung:}$  Ein Sprachcodec dient zur Reduzierung der Datenrate eines digitalisierten Sprach– oder Musiksignals.

• Dabei wird Redundanz und Irrelevanz aus dem Originalsignal entfernt.
• Das Kunstwort „Codec” weist darauf hin, dass die gleiche Funktionseinheit sowohl zur Codierung wie auch zur Decodierung verwendet wird.

Unter anderem wurde der  Adaptive Multi-Rate Codec  (AMR) vorgestellt, der im Frequenzbereich von  $\text{300 Hz}$  bis  $\text{3400 Hz}$  ein dynamisches Umschalten zwischen acht verschiedenen Modi (Einzelcodecs) unterschiedlicher Datenrate im Bereich von  $\text{4.75 kbit/s}$  bis  $\text{12.2 kbit/s}$  erlaubt und auf  ACELP  (Algebraic Code Excited Linear Prediction) basiert.

Auch in UMTS Release 99 und UMTS Release 4 werden diese AMR–Codecs unterstützt. Sie erlauben im Vergleich zu den früheren Sprachcodecs (Full–Rate, Half–Rate und Enhanced Full–Rate Vocoder)

• eine Unabhängigkeit von den Kanalbedingungen und der Netzauslastung,
• die Möglichkeit, die Datenraten an die Bedingungen anzupassen,
• einen verbesserten flexiblen Fehlerschutz bei stärkerer Funkstörung, und
• dadurch insgesamt eine bessere Sprachqualität.

Im Jahre 2001 wurde vom 3gpp–Forum  (3rd Generation Partnership Project)  und der International Telecommuncation Union  (ITU)  für das UMTS Release 5 der neue Sprachcodec  Wideband–AMR  spezifiziert. Dieser ist eine Weiterentwicklung des AMR und bietet

Zusammenstellung der Wideband–AMR–Modi

• eine erweiterte Bandbreite von  $\text{50 Hz}$  bis  $\text{7 kHz}$  $($Abtastfrequenz  $\text{16 kHz})$,
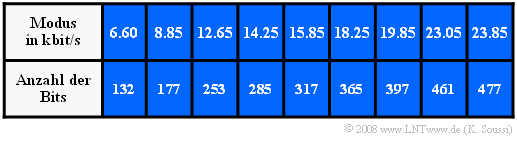
• insgesamt neun Modi zwischen  $\text{6.6 kbit/s}$  und  $\text{23.85 kbit/s}$  (wovon aber nur fünf Modi genutzt werden), und
• eine verbesserte Sprachqualität und einen besseren (natürlicheren) Klang.

Die Tabelle gibt eine Übersicht über die verschiedenen Modi und deren Bitumfang. Sie können sich die Qualität dieser Sprachcodierverfahren bei Sprache und Musik mit dem interaktiven SWF–Applet  Qualität verschiedener Sprach–Codecs  verdeutlichen (Hinweis:  „Nur für „Windows” geeignet!   Adobe Flashplayer erforderlich!).

Anmerkung:   Die untere Grenzfrequenz von Wideband-AMR ist zwar mit  $\text{50 Hz}$ z spezifiziert, aber auf Grund verwendeter Vorfilter ist diese meist – und auch in der Audio–Demo – auf  $\text{200 Hz}$  angehoben, um die Störanfälligkeit zu reduzieren und die Kenndaten von Handy–Lautsprechern und –Mikrofonen zu berücksichtigen.

$\text{Einige Merkmale von Wideband–AMR}$ 

• Die Sprachdaten werden an den Codec als PCM–codierte Sprache mit  $16000$  Abtastwerten pro Sekunde geliefert. Die Sprachcodierung erfolgt in Blöcken von  $\text{20 ms}$  und die Datenrate wird alle  $\text{20 ms}$  angepasst.
• Das Frequenzband  $\text{(50 Hz}$  bis  $\text{7000 Hz})$  wird in zwei Teilbänder unterteilt, die unterschiedlich codiert werden, um mehr Bit den subjektiv wichtigen Frequenzen zuweisen zu können. Das obere Band  $\text{(6400 Hz}$  bis  $\text{7000 Hz})$  wird nur im höchsten Modus $($mit  $\text{23.85 kbit/s)}$  übertragen. In allen anderen Modi werden bei der Codierung nur die Frequenzen  $\text{50 Hz}$  bis  $\text{6400 Hz}$  berücksichtigt.
• Wideband–AMR unterstützt  Discontinuous Transmission  (DTX). Dieses Feature bedeutet, dass die Übertragung bei Sprachpausen angehalten wird, wodurch sowohl der Energieverbrauch der Mobilstation als auch die Gesamtinterferenz an der Luftschnittstelle gesenkt werden. Dieses Verfahren ist auch unter dem Namen  Source–Controlled Rate  (SCR) bekannt.
• Die  Voice Activity Detection  (VAD) ermittelt, ob gerade gesprochen wird oder nicht und fügt auch bei kürzeren Sprachpausen einen SID–Rahmen  (Silence Descriptor)  ein. Dem Teilnehmer wird das Gefühl einer kontinuierlichen Verbindung suggeriert, indem der Decoder während Sprachpausen synthetisch erzeugtes Hintergrundgeräusch  (englisch:  Comfort Noise)  einfügt.

Anwendung des CDMA–Verfahrens bei UMTS

UMTS verwendet das Vielfachzugriffsverfahren  Direct Sequence Code Division Multiple Access  $\rm (DS–CDMA)$, das bereits im Kapitel PN–Modulation  des Buches „Modulationsverfahren” besprochen wurde.

CDMA–Übertragungssystem für zwei Teilnehmer

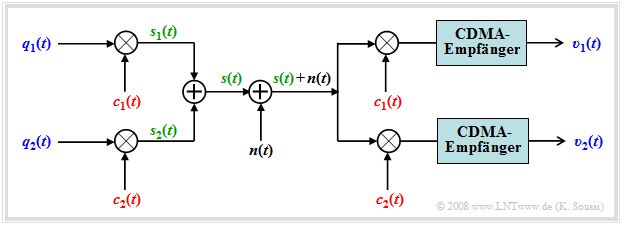
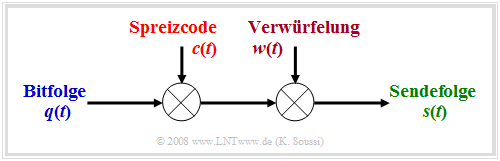
Hier folgt eine kurze Zusammenfassung dieses Verfahrens entsprechend der Grafik, die ein solches System im äquivalenten Tiefpassbereich und stark vereinfacht beschreibt:

• Die beiden Datensignale  $q_1(t)$  und  $q_2(t)$  sollen den gleichen Kanal nutzen, ohne sich gegenseitig zu stören. Die Bitdauer beträgt jeweils  $T_{\rm B}$.
• Jedes der Datensignale wird mit einem zugeordneten Spreizcode –  $c_1(t)$  bzw.  $c_2(t)$  – multipliziert.
• Es wird das Summensignal  $s(t) = q_1(t) · c_1(t) + q_2(t) · c_2(t)$  gebildet und übertragen.
• Beim Empfänger werden die gleichen Spreizcodes  $c_1(t)$  bzw.  $c_2(t)$  zugesetzt und damit die Signale wieder voneinander getrennt.
• Unter der Voraussetzung, dass die Spreizcodes orthogonal sind und dass das AWGN–Rauschen klein ist, gilt für die beiden rekonstruierten Signale am Empfängerausgang:

$$v_1(t) = q_1(t) \ \text{und} \ v_2(t) = q_2(t).$$

• Bei AWGN–Rauschsignal  $n(t)$  und orthogonalen Spreizfolgen wird dabei die Fehlerwahrscheinlichkeit durch andere Teilnehmer nicht verändert.

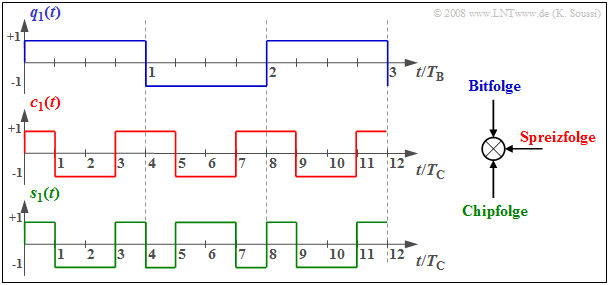
$\text{Beispiel 1:}$  Die Grafik zeigt oben drei Datenbit  $(+1, -1, +1)$  des rechteckförmigen Quellensignals  $q_1(t)$  von Teilnehmer 1, jeweils mit der Symboldauer  $T_{\rm B}$.

Signale bei Direct–Sequence Bandspreizung

• Die Symboldauer  $T_{\rm C}$  des Spreizcodes  $c_1(t)$  – die man auch  Chipdauer  nennt – ist um den Faktor  $4$  kleiner.
• Durch die Multiplikation  $s_1(t) = q_1(t) · c_1(t)$  entsteht ein Chipstrom der Länge  $12 · T_{\rm C}$.

Weiter erkennt man aus dieser Darstellung, dass das Signal  $s_1(t)$  höherfrequenter ist als  $q_1(t)$.

• Deshalb spricht man auch von  Bandspreizung  (englisch:  Spread Spectrum).

• Der CDMA–Empfänger macht diese wieder rückgängig, was als  Bandstauchung  bezeichnet wird.

$\text{Zusammenfassend kann man sagen:}$   Durch die Anwendung von  $\rm (DS–CDMA)$  auf eine Nutzbitfolge

• vergrößert sich dessen Bandbreite um den  Spreizfaktor  $J = T_{\rm B}/T_{\rm C}$ – dieser ist gleich der Anzahl der  Chips pro Bit;
• ist die Chiprate  $R_{\rm C}$  um den Faktor  $J$  größer als die Bitrate  $R_{\rm B}$;
• ist die Bandbreite des gesamten CDMA–Signals um  $J$  größer als die Bandbreite jedes einzelnen Nutzers.

Das heißt:      $\text{Bei UMTS steht jedem Teilnehmer die gesamte Bandbreite über die gesamte Sendedauer zur Verfügung}$.

Erinnern wir uns:  Bei GSM werden als Vielfachzugriffsverfahren sowohl  Frequency Division Multiple Access  als auch  Time Division Multiple Access  verwendet.

• Hier verfügt jeder Teilnehmer nur über ein begrenztes Frequenzband (FDMA), und
• er hat nur innerhalb von Zeitschlitzen Zugriff auf den Kanal (TDMA).

Spreizcodes und Verwürfelung bei UMTS

Die Spreizcodes für UMTS sollen

• zueinander orthogonal sein, um eine gegenseitige Beeinflussung der Teilnehmer zu vermeiden,
• eine flexible Realisierung unterschiedlicher Spreizfaktoren  $J$  ermöglichen.

Der hier dargelegte Sachverhalt wird auch durch das interaktive Applet  OVSF–Codes  verdeutlicht.

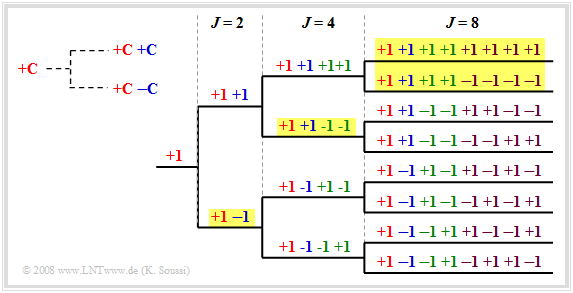
$\text{Beispiel 2:}$  Ein Beispiel hierfür sind die  Codes mit variablem Spreizfaktor  (englisch:  Orthogonal Variable Spreading Faktor, OVSF), die Codes der Längen von  $J = 4$  bis  $J = 512$  bereitstellen. Diese können, wie in der Grafik zu sehen ist, mit Hilfe eines Codebaums erstellt werden. Dabei entstehen bei jeder Verzweigung aus einem Code  $C$  zwei neue Codes  $(+C \ +\hspace{-0.1cm}C)$  und  $(+C \ -\hspace{-0.1cm}C)$.

Schaubild zur OVSF–Codefamilie

Anzumerken ist, dass kein Vorgänger und Nachfolger eines Codes benutzt werden darf.

• Im gezeichneten Beispiel könnten also acht Spreizcodes mit Spreizfaktor  $J = 8$  verwendet werden.
• Auch die vier gelb hinterlegten Codes – einmal mit  $J = 2$, einmal mit  $J = 4$  und zweimal mit  $J = 8$  – sind möglich.
• Die unteren vier Codes mit dem Spreizfaktor  $J = 8$  können aber nicht herangezogen werden, da diese alle mit „$+1 \ –\hspace{-0.1cm}1$” beginnen, was bereits durch den OVSF–Code mit Spreizfaktor  $J = 2$  belegt ist.

Um mehr Spreizcodes zu erhalten und so mehr Teilnehmer versorgen zu können, wird nach der Bandspreizung mit  $c(t)$  die Folge mit  $w(t)$  chipweise nochmals verwürfelt, ohne dass eine weitere Spreizung stattfindet. Der  Verwürfelungscode $w(t)$  hat die gleiche Länge und die selbe Rate wie  $c(t)$.

Zusätzliche Verwürfelung nach Spreizung

Durch die Verwürfelung  (englisch:  Scrambling)  verlieren die Codes ihre vollständige Orthogonalität; man nennt sie quasi–othogonal.

• Bei diesen Codes ist zwar die  Kreuzkorrelationsfunktion  (KKF) zwischen unterschiedlichen Spreizcodes ungleich Null.
• Sie zeichnen sich aber durch eine ausgeprägte  Autokorrelationsfunktion  um den Nullpunkt aus, was die Detektion am Empfänger erleichtert.

Typische Spreiz– und Verwürfelungscodes für UMTS

Die Verwendung quasi–orthogonaler Codes macht Sinn, da die Menge an orthogonalen Codes begrenzt ist und durch die Verwürfelung verschiedene Teilnehmer auch gleiche Spreizcodes verwenden können.





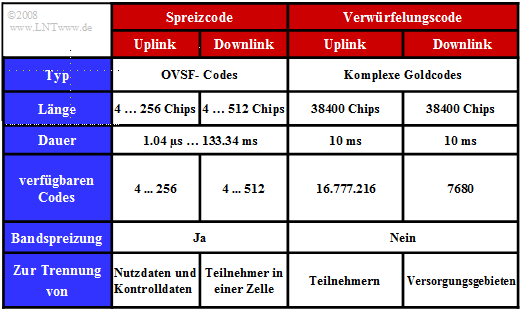
Die Tabelle fasst einige Daten der Spreiz– und Verwürfelungscodes zusammen.

Generator zur Erzeugung von Goldcodes

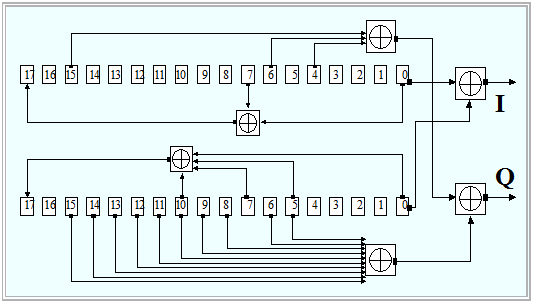
$\text{Beispiel 3:}$  Bei UMTS werden für die Verwürfelung so genannte  Goldcodes  verwendet. Die Grafik aus  [3gpp]  zeigt das Blockschaltbild zur schaltungstechnischen Erzeugung solcher Codes.

• Dabei werden zunächst zwei unterschiedliche Pseudonoise–Folgen gleicher Länge  $($hier:  $N = 18)$  mit Hilfe von Schieberegistern parallel erzeugt und mit  Exklusiv–Oder–Gatter  bitweise addiert.
• Im Uplink hat jede Mobilstation einen eigenen Verwürfelungscode und die Trennung der einzelnen Kanäle erfolgt über den jeweils gleichen Code.
• Dagegen hat im Downlink jedes Versorgungsgebiet eines „Node B„ einen gemeinsamen Verwürfelungscode.

Kanalcodierung bei UMTS

Ebenso wie bei GSM erfahren EFR– und AMR–codierte Sprachdaten im UMTS einen zweistufigen Fehlerschutz, bestehend aus

• Bildung von CRC–Prüfbits  (englisch:  Cyclic Redundancy Check), und
• anschließender Faltungscodierung  (englisch:  Convolutional Coding).

Diese Verfahren unterscheiden sich jedoch von denjenigen bei GSM durch eine größere Flexibilität, da sie bei UMTS unterschiedliche Datenraten berücksichtigen müssen.

Einfügen von CRC– und Tailbits bei UMTS

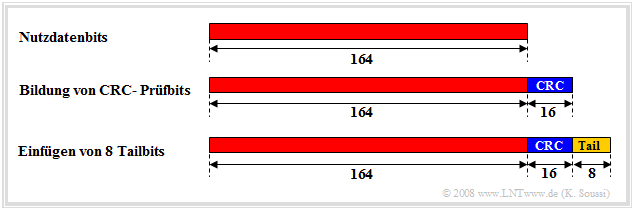
Für die  Fehlererkennung  mittels CRC werden je nach Größe des Transportblockes  $\text{(10 ms}$  oder  $\text{20 ms})$  acht, zwölf, sechzehn oder  $24$  CRC–Bit gebildet und an diesen angehängt.

• Am Ende eines jeden Rahmens werden außerdem acht Tailbits eingefügt, die Synchronisationszwecken dienen.
• Die Grafik zeigt einen beispielhaften Transportblock des DCH–Kanals mit  $164$  Nutzdatenbits, an den  $16$  CRC–Prüfbits und acht Tailbits angehängt werden.

Für die  Fehlerkorrektur  kommen bei UMTS – je nach Datenrate – zwei verschiedene Verfahren zum Einsatz:

• Bei niedrigen Datenraten werden wie bei GSM  Faltungscodes  (englisch:  Convolutional Codes)  mit den Coderaten  $R = 1/2$  oder  $R = 1/3$  verwendet. Diese werden mit acht Speicherelementen eines rückgekoppelten Schieberegisters  $(256$  Zustände$)$ erzeugt. Der Codiergewinn beträgt mit der Coderate  $R = 1/3$  und bei niedrigen Fehlerraten ca.  $4.5$  bis  $6$  dB.
• Bei höheren Datenraten verwendet man  Turbo–Codes  der Rate  $R = 1/3$. Das Schieberegister besteht hier aus drei Speicherzellen, die insgesamt acht Zustände annehmen können. Der Gewinn der Turbo–Codes ist gegenüber Faltungscodes um  $2$  bis  $3$  dB größer und abhängig von der Anzahl der Iterationen. Sie benötigen dafür einen Prozessoren mit hoher Rechenleistung und es kann es zu relativ großen Verzögerungen kommen.

Nach der Kanalcodierung werden die Daten wie bei GSM einer  Interleaver  zugeführt, um empfangsseitig die durch Fading entstandenen Bündelfehler auflösen zu können. Schließlich werden zur  Ratenanpassung  der entstandenen Daten an den physikalischen Kanal einzelne Bit nach einem vorgegebenen Algorithmus entfernt  (Puncturing)  oder wiederholt  (Repetition).

Fehlerkorrekturmechanismen bei UMTS

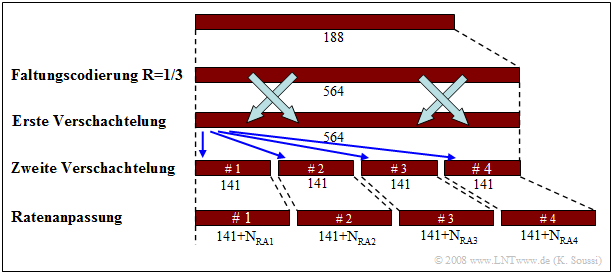
$\text{Beispiel 4:}$  Die Grafik zeigt zunächst die Zunahme der Bits durch einen Faltungs– oder Turbocode der Rate  $R =1/3$, wobei aus dem  $188$–Bit–Zeitrahmen (nach der CRC–Prüfsumme und den Tailbits) ein  $564$–Bit–Rahmen entsteht.

• Danach folgt eine erste externe Verschachtelung und dann eine zweite interne Verschachtelung.
• Nach dieser wird der Zeitrahmen in vier Unterrahmen mit jeweils  $141$  Bit aufgeteilt und diese werden anschließend durch eine Ratenanpassung an den physikalischen Kanal angepasst.

Frequenzgänge und Impulsformung bei UMTS

Blockschaltbild des optimalen Nyquistentzerrers bei idealem Kanal

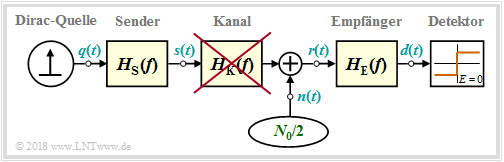
In diesem Abschnitt gehen wir von folgendem Blockschaltbild eines Binärsystems bei idealem Kanal aus   ⇒   $H_{\rm K}(f) = 1$.

Insbesondere gelte:

• Das  Sendeimpulsfilter  wandelt die binären  $\{0, \ 1\}$ Daten in physikalische Signale. Das Filter wird beschrieben durch den Frequenzgang  $H_{\rm S}(f)$, der formgleich mit dem Spektrum eines einzelnen Sendeimpulses ist.

• Bei UMTS ist das Empfangsfilter  $H_{\rm E}f) = H_{\rm S}(f)$  an den Sender angepasst  (Matched–Filter)  und der Gesamtfrequenzgang  $H(f) = H_{\rm S}(f) · H_{\rm E}(f)$  erfüllt das  erste Nyquistkriterium:

$$ H(f) = H_{\rm CRO}(f) = \left\{ \begin{array}{c} 1 \\ 0 \\ \cos^2 \left( \frac {\pi \cdot (|f| - f_1)}{2 \cdot (f_2 - f_1)} \right)\end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}}\\ {\rm sonst }\hspace{0.05cm}. \end{array} \begin{array}{*{20}c} |f| \le f_1, \\ |f| \ge f_2,\\ \\\end{array}$$

Das bedeutet:   Zeitlich aufeinander folgende Impulse stören sich nicht gegenseitig   ⇒   es treten keine  Impulsinterferenzen  (englisch:  Intersymbol Interference, ISI) auf. Die zugehörige Zeitfunktion lautet:

$$h(t) = h_{\rm CRO}(t) ={\rm si}(\pi \cdot t/ T_{\rm C}) \cdot \frac{\cos(r \cdot \pi t/T_{\rm C})}{1- (2r \cdot t/T_{\rm C})^2}. $$

• „CRO” steht hierbei für  Cosinus–Rolloff  (englisch:  Raised Cosine).
• Die Summe  $f_1 + f_2$  ist gleich dem Kehrwert der Chipdauer  $T_{\rm C} = 260 \ \rm ns$, also gleich  $3.84 \ \rm MHz$.
• Der  Rolloff–Faktor  (wir bleiben bei der in  $\rm LNTwww$  gewählten Bezeichnung  $r$, im UMTS–Standard wird hierfür  $\alpha$  verwendet)

$$r = \frac{f_2 - f_1}{f_2 + f_1} $$

wurde bei UMTS zu  $r = 0.22$  festgelegt. Die beiden Eckfrequenzen sind somit

$$f_1 = {1}/(2 T_{\rm C}) \cdot (1-r) \approx 1.5\,{\rm MHz}, \hspace{0.2cm} f_2 ={1}/(2 T_{\rm C}) \cdot (1+r) \approx 2.35\,{\rm MHz}.$$

• Die erforderliche Bandbreite beträgt  $B = 2 · f_2 = 4.7 \ \rm MHz$. Für jeden UMTS–Kanal steht somit mit  $5 \ \rm MHz$  ausreichend Bandbreite zur Verfügung.

Cosinus–Rolloff–Spektrum und Impulsantwort

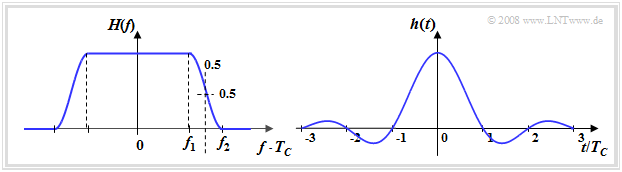
$\text{Fazit:}$  Die Grafik zeigt

• links das (normierte) Nyquistspektrum  $H(f)$, und
• rechts den zugehörigen Nyquistimpuls  $h(t)$, dessen Nulldurchgänge im Abstand  $T_{\rm C}$  äquidistant sind.

$\text{Es ist zu beachten:}$

• Das Sendefilter  $H_{\rm S}(f)$  und das Matched–Filter  $H_{\rm E}(f)$  sind jeweils  Wurzel–Cosinus–Rolloff–förmig  (englisch:  Root Raised Cosine). Erst das Produkt  $H(f) = H_{\rm S}(f) · H_{\rm E}(f)$  führt zum Cosinus–Rolloff.
• Das bedeutet auch:   Die Impulsantworten  $h_{\rm S}(t)$  und  $h_{\rm E}(t)$  erfüllen für sich allein die erste Nyquistbedingung nicht. Erst die Kombination aus beiden (im Zeitbereich die Faltung) führt zu den gewünschten äquidistanten Nulldurchgängen.

Modulationsverfahren bei UMTS

Die bei UMTS eingesetzten  Modulationsverfahren  können wie folgt zusammengefasst werden:

• In der Abwärtsrichtung  (Downlink)  wird zur Modulation  Quaternary Phase Shift Keying  (QPSK) verwendet – sowohl bei FDD  als auch bei TDD. Dabei werden Nutzdaten (DPDCH–Kanal) und Kontrolldaten (DPCCH–Kanal) zeitlich gemultiplext.
• Bei TDD  wird das Signal in Aufwärtsrichtung  (Uplink)  ebenfalls mittels QPSK moduliert, nicht aber bei FDD. Hier wird vielmehr eine  zweifache binäre PSK  (englisch:  Dual Channel–BPSK) verwendet.

Bei  Dual–Channel BPSK  wird zwar ebenfalls der QPSK–Signalraum genutzt, aber in Inphase– und Quadratur–Komponente  werden unterschiedliche Kanäle übertragen. Pro Modulationsschritt werden also zwei Chips übertragen. Die Brutto–Chiprate ist daher doppelt so groß wie die Modulationsrate von  $3.84$ Mchip pro Sekunde.

Zweifache BPSK (Binary Phase Shift Keying)

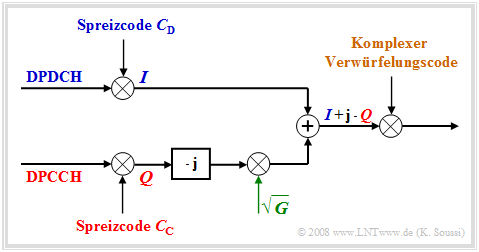
$\text{Beispiel 5:}$  Die Grafik zeigt dieses I/Q–Multiplexing–Verfahren, wie es auch bezeichnet wird, im äquivalenten Tiefpassbereich:

• Die gespreizten Nutzdaten des DPDCH–Kanals werden auf die Inphase–Komponente und die gespreizten Kontrolldaten des DPCCH–Kanals auf die Quadratur–Komponente moduliert und übertragen.
• Nach der Modulation wird die Quadratur–Komponente mit der Wurzel des Leistungsverhältnisses  $G$  zwischen den beiden Kanälen gewichtet, um den Einfluss des Leistungsunterschieds zwischen  $I$  und  $Q$  zu minimieren.
• Abschließend wird das komplexe Summensignal  $(I +{\rm j} · Q)$  mit einem ebenfalls komplexen Verwürfelungscode multipliziert.

$\text{Fazit:}$  Ein Vorteil der zweifachen BPSK–Modulation ist die Möglichkeit der Verwendung  stromsparender Verstärker.

• Zeitmultiplex von Nutz– und Kontrolldaten wie im  Uplink  ist aber im  Downlink  nicht möglich.
• Ein Grund hierfür ist der Einsatz von  Discontinuous Transmission  (DTX) und die damit verbundenen zeitlichen Einschränkungen.

Single–User–Empfänger

Aufgabe eines CDMA–Empfängers ist es, aus der Summe der gespreizten Datenströme die gesendeten Daten der einzelnen Teilnehmer zu separieren und zu rekonstruieren. Dabei unterscheidet man zwischen  Single–User–Empfängern und  Multi–User–Empfängern.

Im Downlink von UMTS wird stets ein  Single–User–Empfänger verwendet, da in der Mobilstation eine gemeinsame Detektion aller Teilnehmer wegen der Vielzahl aktiver Teilnehmer sowie der Länge der Verwürfelungscodes und des asynchronen Betriebs zu aufwändig wäre.

Ein solcher Empfänger besteht aus einer Bank unabhängiger Korrelatoren. Jeder einzelne der insgesamt  $J$  Korrelatoren gehört zu einer spezifischen Spreizfolge. Die Korrelation wird meist in einer so genannten  Korrelatordatenbank  softwaremäßig gebildet.

Dabei erhält man am Korrelatorausgang die Summe aus

• der  Autokorrelationsfunktion  des Spreizcodes und
• der  Kreuzkorrelationsfunktion  aller anderen Teilnehmer mit dem teilnehmereigenen Spreizcode.

Single–User–Empfänger mit Matched–Filter

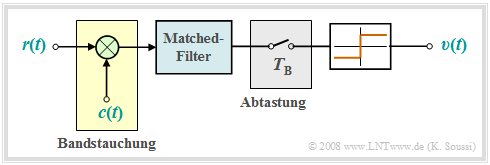
Die Grafik zeigt die einfachste Realisierung eines solchen Empfängers mit Matched–Filter.

• Das Empfangssignal  $r(t)$  wird zunächst mit dem Spreizcode  $c(t)$  des betrachteten Teilnehmers multipliziert, was als  Bandstauchung  oder  Entspreizung  bezeichnet wird (gelbe Hinterlegung).
• Danach folgt die Faltung mit der Impulsantwort des Matched–Filters  (Root Raised Cosine), um das SNR zu maximieren, und die Abtastung im Bittakt  ( $T_{\rm B}$ ).
• Abschließend erfolgt die Schwellenwertentscheidung, die das Sinkensignal  $v(t)$ und  damit die Datenbit des betrachteten Teilnehmers liefert.

$\text{Bitte beachten Sie:}$ 

Beim AWGN–Kanal haben die Bandspreizung beim Sender und die daran angepasste Bandstauchung beim Empfänger wegen  $c(t)^2 = 1$  keinen Einfluss auf die Bitfehlerwahrscheinlichkeit. Wie in  Aufgabe 4.5  gezeigt wird, gilt auch mit Bandspreizung/Bandstauchung bei optimalem Empfänger unabhängig vom Spreizgrad  $J$:

$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B} }/{N_{\rm 0} } } \hspace{0.05cm} \right )\hspace{0.05cm}. $$

Dieses Ergebnis lässt sich wie folgt begründen:
Die statistischen Eigenschaften von weißem Rauschen  $n(t)$  werden durch die Multiplikation mit dem  $±1$–Signal  $c(t)$  nicht verändert.

RAKE–Empfänger

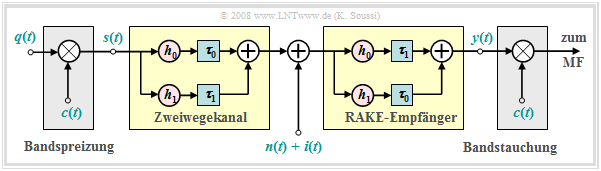
Ein weiterer Empfänger für die Single–User–Detektion ist der  RAKE–Empfänger, der bei einem Mehrwegekanal zu deutlichen Verbesserungen führt. Die Grafik zeigt seinen Aufbau für einen Zweiwegekanal mit 

Struktur des RAKE–Empfängers (Darstellung im äquivalenten Tiefpassbereich)

• einem direkten Pfad mit Koeffizient  $h_0$  und Verzögerungszeit  $τ_0$,
• einem Echo mit Koeffizient  $h_1$  und Verzögerungszeit  $τ_1$.

Zur Vereinfachung werden hier die Koeffizienten  $h_0$  und  $h_1$  als reell angenommen. Aufgrund der Darstellung im äquivalenten Tiefpassbereich könnten diese auch komplex sein.

Aufgabe des RAKE–Empfängers ist es, die Signalenergien aller Pfade  (in diesem Beispiel nur zwei)  auf einen einzigen Zeitpunkt zu konzentrieren. Er arbeitet demnach wie eine  Harke  für den Garten, was auch die deutsche Übersetzung für „RAKE” ist.
Legt man einen Diracimpuls zur Zeit  $t = 0$  an den Kanaleingang an, so gibt es am Ausgang des RAKE–Empfängers drei Diracimpulse:

$$ s(t) = \delta(t) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} y(t) = h_0 \cdot h_1 \cdot \delta(t - 2\tau_0) + (h_0^2 + h_1^2) \cdot \delta(t - \tau_0 - \tau_1)+ h_0 \cdot h_1 \cdot \delta(t - 2\tau_1) .$$

• Die Signalenenergie konzentriert sich auf den Zeitpunkt  $τ_0 + τ_1$. Von den insgesamt vier Wegen tragen zwei dazu bei (mittlerer Term).
• Die Diracfunktionen bei  $2τ_0$  und  $2τ_1$  bewirken zwar Impulsinterferenzen. Ihre Gewichte sind aber deutlich kleiner als die des Hauptpfades.

$\text{Beispiel 6:}$  Mit den Kanalparametern  $h_0 = 0.8$  und  $h_1 = 0.6$  beinhaltet der Hauptpfad $($mit Gewicht  $h_0)$  nur  $0.82/(0.82 + 0.62) = 64\%$  der gesamten Signalenergie. Mit RAKE–Empfänger und den gleichen Gewichten lautet die obige Gleichung:

$$ y(t) = 0.48 \cdot \delta(t - 2\tau_0) + 1.0 \cdot \delta(t - \tau_0 - \tau_1)+ 0.48 \cdot \delta(t - 2\tau_1) .$$

Der Anteil des Hauptpfades an der Gesamtenergie beträgt nun  ${1^2}/{(1^2 + 0.48^2 + 0.48^2)} ≈ 68\%.$

RAKE–Empfänger werden zur Implementierung in mobilen Geräten bevorzugt, sind aber bei vielen aktiven Teilnehmern nur begrenzt leistungsfähig. Bei einem Mehrwegekanal mit vielen  $(M)$  Pfaden hat auch der RAKE  $M$  Finger. Der Hauptfinger  (Main Finger)  – auch Searcher  genannt – ist dafür verantwortlich, die individuellen Pfade der Mehrfachausbreitung zu identifizieren und einzuordnen. Er sucht die stärksten Pfade und weist diese zusammen mit ihren Steuerinformationen anderen Fingern zu. Dabei wird die Zeit– und Frequenzsynchronisation aller Finger kontinuierlich mit den Kontrolldaten des empfangenen Signals verglichen.

Multi–User–Empfänger

Bei einem Single–User–Empfänger wird nur das Datensignal eines Teilnehmers entschieden, während alle anderen Teilnehmersignale als zusätzliches Rauschen betrachtet werden. Die Fehlerrate eines solchen Detektors wird jedoch dann sehr groß sein, wenn große  Intrazellinterferenzen  (viele aktive Teilnehmer in der betrachteten Funkzelle) oder  Interzellinterferenzen  (stark störende Teilnehmer in Nachbarzellen) vorliegen.

Dagegen treffen  Multi–User–Empfänger  (Mehrbenutzerempfänger)  eine gemeinsame Entscheidung für alle aktiven Teilnehmer. Deren Eigenschaften können wie folgt zusammengefasst werden:

• Ein Multi–User–Empfänger betrachtet die Interferenzen anderer Teilnehmer nicht als Rauschen, sondern nutzt auch die in den Interferenzsignalen enthaltenen Informationen zur Detektion.
• Der Empfänger ist aufwändig zu realisieren und die Algorithmen sind äußerst rechenintensiv. Er beinhaltet eine extrem große Korrelatordatenbank gefolgt von einem gemeinsamen Detektor.
• Dem Multi–User–Empfänger müssen die Spreizcodes aller aktiven Teilnehmer bekannt sein. Diese Voraussetzung schließt einen Einsatz im UMTS–Downlink (also bei der Mobilstation) aus. Dagegen sind den Basisstationen alle teilnehmerspezifischen Spreizcodes a priori bekannt, so dass im Uplink die Mehrbenutzerdetektion auch tatsächlich zur Anwendung kommt.
• Manche Detektionsalgorithmen verlangen zusätzlich die Kenntnis anderer Signalparameter wie Energien und Verzögerungszeiten. Der gemeinsame Detektor – das Herzstück des Empfängers – ist dafür verantwortlich, den jeweiligen passenden Detektionsalgorithmus anzuwenden. Beispiele für die Mehrbenutzerdetektion sind  Decorrelating Detection  und  Interference Cancellation.

Near–Far–Effekt

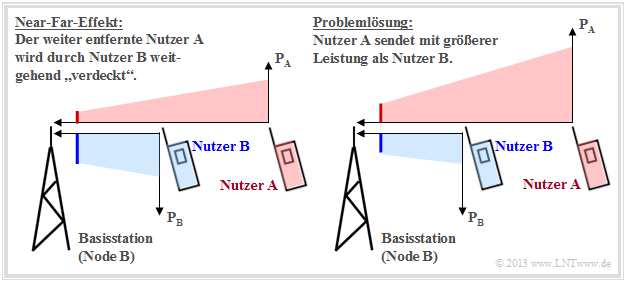
Der Near–Far–Effekt ist ausschließlich ein Problem des Uplinks, also der Übertragung von mobilen Teilnehmern zu einer Basisstation. Wir betrachten ein Szenario mit zwei unterschiedlich weit von der Basisstation entfernten Nutzern entsprechend folgender Grafik. Diese kann man wie folgt interpretieren:

Szenarien zum Near–Far–Effekt

• Senden beide Mobilstationen mit gleicher Leistung, so ist die Empfangsleistung des roten Nutzers  $\rm A$  an der Basisstation aufgrund des Pfadverlustes deutlich kleiner als die des blauen Nutzers  $\rm B$ (linkes Szenario). In großen Makrozellen kann der Unterschied bis zu  $100 \ \rm dB$  ausmachen. Dadurch wird das rote Signal weitgehend durch das blaue verdeckt.

• Man kann den Near–Far–Effekt weitgehend vermeiden, wenn der weiter entfernte Nutzer  $\rm A$  mit höherer Leistung sendet als Nutzer  $\rm B$, wie im rechten Szenario angedeutet. An der Basisstation ist dann die Empfangsleistung beider Mobilstationen (nahezu) gleich.

Anmerkung:   Bei einem idealisierten System  (Einwegekanal, ideale A/D–Wandler, vollständig lineare Verstärker ) sind die übertragenen Daten der Nutzer orthogonal zueinander und man könnte die Nutzer auch bei sehr unterschiedlichen Empfangsleistungen einzeln detektieren. Diese Aussage gilt für UMTS  (Mehrfachzugriffsverfahren:  CDMA)  ebenso wie für für das 2G–System GSM  (FDMA/TDMA)  und für das 4G–System LTE  (TDMA/OFDMA).

In der Realität ist jedoch die Orthogonalität aufgrund folgender Ursachen nicht immer gegeben:

• verschiedene Empfangspfade   ⇒   Mehrwegekanal,
• nicht ideale Eigenschaften der Spreiz– und Scramblingcodes bei CDMA,
• Asynchronität der Nutzer im Zeitbereich  (Grundlaufzeit der Pfade),
• Asynchronität der Nutzer im Frequenzbereich  (nicht ideale Oszillatoren und Dopplerverschiebung aufgrund der Mobilität der Nutzer).

Folglich sind die Nutzer nicht mehr orthogonal zueinander und der Störabstand des zu detektierenden Nutzers gegenüber den anderen Teilnehmern ist nicht beliebig hoch. Bei  GSM  und  LTE  kann man von Störabständen von  $25 \ \rm dB$  und mehr ausgehen, bei UMTS (CDMA) jedoch nur von ca.  $15 \ \rm dB$, bei hochratiger Datenübertragung eher noch von etwas weniger.

Träger–zu–Interferenz–Leistungsverhältnis (CIR)

Unter  Kapazität  wird allgemein die Anzahl der verfügbaren Übertragungskanäle pro Zelle verstanden werden. Da aber bei UMTS die Teilnehmerzahl im Gegensatz zum GSM nicht streng begrenzt ist, lässt sich hier keine feste Kapazität angeben.

• Bei perfekten Codes stören sich die Teilnehmer gegenseitig nicht. Dadurch wird die maximale Nutzerzahl allein durch den Spreizfaktor  $J$  und die verfügbare Anzahl der zueinander orthogonalen Codes bestimmt, die aber ebenfalls limitiert ist.
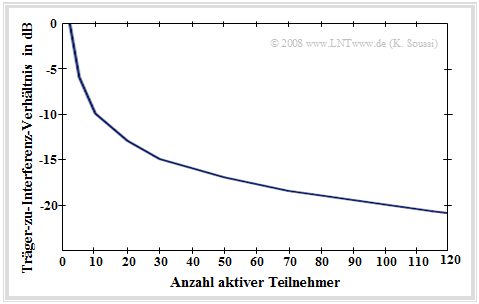
• Praxisnäher sind nichtperfekte, nur quasi–orthogonale Codes. Hier wird die „Kapazität” einer Funkzelle vorwiegend durch die entstehenden Interferenzen bzw. das  Träger–zu–Interferenz–Leistungsverhältnis  (englisch:  Carrier–to–Interference Ratio, CIR) bestimmt.

Carrier–to–Interference Ratio  („CIR”) abhängig von der Teilnehmerzahl

Wie aus dieser Grafik zu ersehen ist, hängt das „CIR” direkt von der Anzahl aktiver Teilnehmer ab. Je mehr Teilnehmer aktiv sind, desto mehr Interferenzleistung entsteht und desto kleiner wird das „CIR”.

Desweiteren hängt dieses für UMTS entscheidende Kriterium auch von folgenden Größen ab:

• der Topologie und dem Nutzerverhalten (aufgerufene Dienste),
• dem Spreizfaktor  $J$  und der Orthogonalität des verwendeten Spreizcodes.

Um den störenden Einfluss der Interferenzleistung auf die Übertragungsqualität zu begrenzen, gibt es zwei Möglichkriten:

• Zellatmung:  Nimmt bei UMTS die Anzahl der aktiven Teilnehmer signifikant zu, so wird der Zellenradius verkleinert und  (wegen der nun weniger Teilnehmer in der Zelle)  auch die aktuelle Interferenzleistung geringer. Für die Versorgung der Teilnehmer am Rande der verkleinerten Zelle springt dann eine weniger belastete Nachbarzelle ein.
• Leistungsregelung:  Überschreitet die Gesamtinterferenzleistung innerhalb einer Funkzelle einen vorgegebenen Grenzwert, so wird die Sendeleistung aller Teilnehmer entsprechend herabgesetzt und/oder die Datenrate reduziert, was eine schlechtere Übertragungsqualität für alle zur Folge hat. Hierzu mehr auf der nächsten Seite.

Leistung und Leistungsregelung in UMTS

Als Regelgröße bei der Leistungsregelung in UMTS wird das Verhältnis zwischen der Signalleistung und der Interferenzleistung verwendet. Dabei gibt es Unterschiede zwischen dem FDD– und TDD–Modus.

Leistungsregelung im FDD–Modus

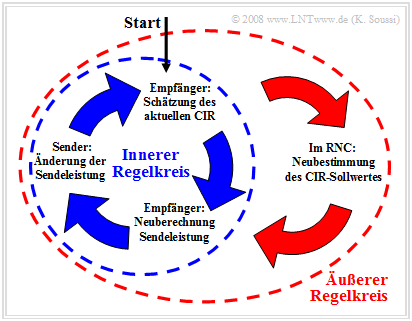
Wir betrachten die  Leistungsregelung im FDD–Modus  genauer. In der Grafik erkennt man zwei verschiedene Regelkreise:

• Der  innere Regelkreis  steuert die Sendeleistung auf der Basis von Zeitschlitzen, wobei in jedem Zeitschlitz ein Leistungskommando übertragen wird. Die Leistung des Senders wird mit Hilfe der CIR–Schätzungen im Empfänger und den Vorgaben des  Radio Network Controllers  (RNC) aus dem äußeren Regelkreis bestimmt und verändert.
• Der  äußere Regelkreis  regelt auf Basis von Rahmen mit $10$ Millisekunden Dauer. Er wird im RNC realisiert und ist dafür zuständig, den Soll–Wert für den inneren Regelkreis zu bestimmen.

Der Ablauf der FDD–Leistungsregelung sieht folgendermaßen aus:

• Der RNC gibt einen Sollwert für das Träger–zu–Interferenz–Verhältnis (CIR–Sollwert) vor.
• Der Empfänger schätzt den CIR–Istwert und generiert Steuerkommandos für den Sender.
• Der Sender ändert entsprechend dieser Steuerkommandos die Sendeleistung.

Das Prinzip der  Leistungsregelung im TDD–Modus  ähnelt der oben vorgestellten Regelung für den FDD–Modus, in der Abwärtsrichtung sind sie sogar praktisch identisch.

$\text{Fazit:}$  Die  TDD–Leistungsregelung  ist viel langsamer und dadurch auch unpräziser als bei  FDD. Eine schnelle Leistungsregelung ist in diesem Fall aber auch gar nicht möglich, da jeder Teilnehmer jeweils nur einen Bruchteil des Zeitrahmens zur Verfügung hat.

Link–Budget

Bei der Planung von UMTS–Netzen ist die Berechnung des Link-Budgets ein wichtiger Schritt. Die Kenntnis des Link–Budgets ist sowohl bei der Dimensionierung der Versorgungsgebiete als auch für die Bestimmung der Kapazität und der Dienstgüte–Anforderungen erforderlich.

Ziel des Link–Budgets  ist die Berechnung der  maximalen Zellgröße  unter Berücksichtigung folgender Kriterien:

• Art und Datenrate der Services,
• Topologie der Umgebung,
• Systemkonfiguration (Lage und Leistung der Basisstationen, Handover–Gewinn),
• Service–Anforderungen (Verfügbarkeit),
• Art der Mobilstation (Geschwindigkeit, Leistung),
• finanzielle und wirtschaftliche Aspekte.

Budget für einen Sprachübertragungskanal

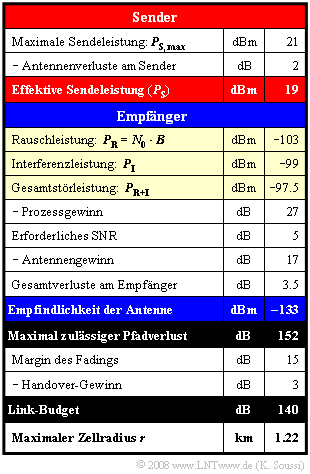
$\text{Beispiel 7:}$  Die Berechnung des Link–Budgets wird am Beispiel eines Sprachübertragungskanals im UMTS–Downlink dargestellt. Zu den beispielhaften Zahlenwerten ist zu bemerken:

• Die Sendeleistung betrage  $P_{\rm S} =19 \ \rm dBm$, was ca.  $79 \ \rm mW$  entspricht. Hierbei ist der Antennenverlust mit  $2\ \rm dB$  berücksichtigt.
• Die Rauschleistung  $P_{\rm R} = 5 · 10^{-11} \ \rm mW$  ist das Produkt aus UMTS–Bandbreite und Rauschleistungsdichte  
    ⇒   $P_{\rm R} = -103 \ \rm dBm $.
• Die Interferenzleistung ist  $P_{\rm I} = –99\ \rm dBm$  entsprechend  $1.25 · 10^{-10} \ \rm mW$.
• Damit ergibt sich die gesamte Störleistung zu  $P_{\rm R+I} = P_{\rm R} + P_{\rm I} = 1.25 · 10^{-10} \ \rm mW$ 
    ⇒   $P_{\rm R+I} =- 97.5\ \rm dBm$.
• Die Antennenempfindlichkeit ergibt sich zu  $-97.5 - 27 + 5 - 17 + 3.5 = - 133 \ \rm dBm$. Ein großer negativer Wert ist hierbei „gut”.
• Der maximal zulässige Pfadverlust soll möglichst groß sein. Man erhält im Beispiel  $19 - (-133) = 152 \ \rm dB$.
• Das  Link–Budget  beinhaltet den Margin für Fading und den Handover–Gewinn und beträgt im Beispiel  $140 \ \rm dB$.
• Der maximale Zellradius lässt sich aus dem Link–Budget mit einer empirischen Formel von Okumura–Hata bestimmen. Es gilt:

$$ {r}\ [{\rm km}] = 10^{({\rm LinkBudget}- 137)/35}= 10^{0.0857}\approx 1.22 . $$

Anmerkungen:  

• Die Angabe  $\rm dB$  kennzeichnet eine logarithmische Leistungsangabe, bezogen auf  $1 \ \rm W$.
• Dagegen bezieht sich  $\rm dBm$  auf die Leistung  $1 \ \rm mW$.

UMTS–Funkressourcenverwaltung

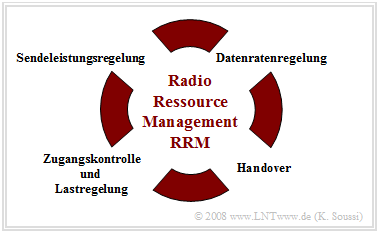
Zentrale Aufgabe der  Funkressourcenverwaltung  (englisch:  Radio Resource Management, RRM) ist die dynamische Anpassung der Funkübertragungsparameter an die aktuelle Situation  (Fading, Bewegung der Mobilstation, Auslastung, usw.)  mit dem Ziel,

Radio Resource Management in UMTS

• die Übertragungs– und Teilnehmerkapazitäten zu steigern,
• die individuelle Übertragungsqualität zu verbessern und
• die vorhandenen Funkressourcen ökonomisch zu nutzen.

Nachfolgend werden die im Schaubild zusammengestellten wichtigsten RRM–Mechanismen erläutert.

Sendeleistungsregelung
Das  Radio Resource Management  versucht, die Empfangsleistung und damit das Träger–zu–Interferenz–Verhältnis (CIR) am Empfänger konstant zu halten oder zumindest zu vermeiden, dass ein vorgegebener Grenzwert unterschritten wird.

Ein Beispiel für die Notwendigkeit der Leistungsregelung ist der  Near–Far–Effekt, der bekanntlich zu einem Verbindungsabbruch führen kann.

Die Schrittweite der Leistungsregelung beträgt  $1 \ \rm dB$  oder  $2 \ \rm dB$, die Frequenz der Regelungskommandos ist  $1500$  Kommandos pro Sekunde.

Regelung der Datenrate
Bei UMTS ist ein Austausch zwischen Datenrate und Übertragungsqualität möglich, die sich über die Wahl des Spreizfaktors realisieren lässt. Eine Verdopplung des Spreizfaktors entspricht hierbei einer Halbierung der Datenrate und erhöht die Qualität um  $3\ \rm dB$  (Spreizgewinn).

Zugangskontrolle
Um Überlastsituationen im Gesamtnetz zu vermeiden, wird vor dem Aufbau einer neuen Verbindung überprüft, ob die notwendigen Ressourcen vorhanden sind. Andernfalls wird die neue Verbindung abgewiesen. Diese Überprüfung wird durch Abschätzung der Sendeleistungsverteilung nach der Aufnahme der neuen Verbindung realisiert.

Lastregelung
Diese wird aktiv, wenn trotz Zugangskontrolle eine Überlast auftritt. In diesem Fall wird ein Handover zu einem anderen „Node B” initiiert und – falls dies nicht möglich ist – werden die Datenraten bestimmter Teilnehmer gesenkt.

Handover
Die Funkressourcenverwaltung ist schließlich auch für das Handover verantwortlich, um unterbrechungsfreie Verbindungen zu gewährleisten. Die Zuordnung der Mobilstationen zu den einzelnen Funkzellen erfolgt auf Grundlage von CIR–Messungen.

Aufgaben zum Kapitel

Aufgabe 4.5: Pseudo Noise-Modulation

Aufgabe 4.5Z: Zur Bandspreizung bei UMTS

Aufgabe 4.6: OVSF-Codes

Aufgabe 4.7: Zum RAKE-Empfänger