Difference between revisions of "Channel Coding/Objective of Channel Coding"
| Line 39: | Line 39: | ||
| − | All ' | + | All '''ARQ''' (Automatic Repeat Request) procedures use error detection only. Less redundancy is required for error detection than for error correction. One disadvantage of ARQ is its low throughput when channel quality is poor, i.e. when entire blocks of data must be frequently re-requested by the receiver.<br> |
In this book we mostly deal with '''Forward Error Correction''' which leads to very small error rates if the channel is sufficiently good (large SNR). With worse channel conditions, nothing changes in the throughput, i.e. the same amount of information is transmitted. However, the error rate can then assume very large values.<br> | In this book we mostly deal with '''Forward Error Correction''' which leads to very small error rates if the channel is sufficiently good (large SNR). With worse channel conditions, nothing changes in the throughput, i.e. the same amount of information is transmitted. However, the error rate can then assume very large values.<br> | ||
| Line 55: | Line 55: | ||
:$$0000\boldsymbol{0}, 0001\boldsymbol{1}, \text{...} , 1111\boldsymbol{0}, \text{...}\ ,$$ | :$$0000\boldsymbol{0}, 0001\boldsymbol{1}, \text{...} , 1111\boldsymbol{0}, \text{...}\ ,$$ | ||
| − | it is very easy to recognise a single error. Two errors within a code word, on the other hand, remain undetected. | + | it is very easy to recognise a single error. Two errors within a code word, on the other hand, remain undetected. }}<br> |
| Line 83: | Line 83: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Example 3: | + | $\text{Example 3: Barcode (one-dimensional)}$ |
| − | <br> | + | <br>The most widely used error-detecting code worldwide is the bar code or bar code (English: <i>Bar Code</i>) for marking products, for example according to EAN–13 (<i>European Article Number</i> ) with 13 digits. |
[[File:P ID2330 KC T 1 1 S2.png|right|frame|1D–Barcode]] | [[File:P ID2330 KC T 1 1 S2.png|right|frame|1D–Barcode]] | ||
| − | * | + | *These are represented by bars and gaps of different widths and can be easily decoded with an opto–cial reader. |
| − | * | + | *The first three digits indicate the country (for example Germany: between 400 and 440), the next four or five digits the manufacturer and the product. |
| − | * | + | *The last digit is the check digit $z_{13}$, which is calculated exactly as for ISBN–13.}} |
| − | == | + | == Some Introductory Examples of Error Correction== |
<br> | <br> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4: 2D–Barcodes For Online–Tickets}$ |
| − | <br> | + | <br>If you book a Deutsche Bahn ticket online and print it out, you will find an example of a two-dimensional barcode, namely the [https://en.wikipedia.org/wiki/Aztec_Code Aztec–Code] developed in 1995 by Andy Longacre at the Welch Allyn company in the USA, with which amounts of data up to $3000$ characters can be encoded. Due to the [[Channel_Coding/Definition_und_Eigenschaften_von_Reed–Solomon–Codes|Reed–Solomon–error correction]] reconstruction of the data content is still possible even if up to $40\%$ of the code has been destroyed, for example by bending the ticket or by coffee stains.<br> |
| − | [[File:P ID2332 KC T 1 1 S2a.png|center|frame|2D–Barcodes: Aztec– | + | [[File:P ID2332 KC T 1 1 S2a.png|center|frame|2D–Barcodes: Aztec– And QR–Code|class=fit]] |
| − | + | On the right is a $\rm QR–Code$ (<i>Quick Response</i>) with associated content. The QR–code was developed in 1994 for the automotive industry in Japan to mark components and also allows error correction. In the meantime, the use of the QR–code has become very diverse. In Japan, it can be found on almost every advertising poster and on every business card. It is also becoming more and more popular in Germany.<br> | |
| − | + | All 2D–barcodes have square markings to calibrate the reader. You can find details on this in [KM+09]<ref>Kötter, R.; Mayer, T.; Tüchler, M.; Schreckenbach, F.; Brauchle, J.: ''Channel Coding''. Lecture Notes, Lehrstuhl für Nachrichtentechnik, TU München, 2008.</ref>.}} | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 5: Codes For Satellites– And Space Communications}$ |
| − | <br> | + | <br>One of the first areas of application of error correction methods was communication from/to satellites and space shuttles, i.e. transmission routes characterised by low transmission powers and large path losses. As early as 1977, channel coding was used in the <i>space–mission Voyager 1</i> to Neptune and Uranus, in the form of serial concatenation of a [[Channel_Coding/Definition_und_Eigenschaften_von_Reed–Solomon–Codes|Reed–Solomon–Code]] and a [[Channel_Coding/Grundlagen_der_Faltungscodierung|convolutional code]].<br> |
| − | + | Thus, the power parameter $10 · \lg \; E_{\rm B}/N_0 \approx 2 \, \rm dB$ was already sufficient to achieve the required error rate $5 · 10^{-5}$ (related to the compressed data after source coding). Without channel coding, on the other hand, almost $9 \, \rm dB$ are required for the same error rate, i.e. a factor $10^{0.7} ≈ 5$ greater transmission power.<br> | |
| − | + | The planned Mars project (data transmission from Mars to Earth with $\rm 5W$–lasers) will also only be successful with a sophisticated coding scheme}}<br>. | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 6: Channel Codes For Mobile Communikations}$ |
| − | <br> | + | <br>A further and particularly high-turnover application area that would not function without channel coding is mobile communication. Here, unfavourable conditions without coding would result in error rates in the percentage range and, due to shadowing and multipath propagation (echoes), the errors often occur in bundles. The error bundle length is sometimes several hundred bits. |
| − | * | + | *For voice transmission in the GSM–system, the $182$ most important (class 1a and 1b) of the total 260 bits of a voice frame $(20 \, \rm ms)$ together with a few parity– and tailbits are convolutionally coded $($with memory $m = 4$ and rate $R = 1/2)$ and scrambled. Together with the $78$ less important and therefore uncoded bits of class 2, this results in the bit rate increasing from $13 \, \rm kbit/s$ to $22.4 \, \rm kbit/s$ .<br> |
| − | * | + | *One uses the (relative) redundancy of $r = (22.4 - 13)/22.4 ≈ 0.42$ for error correction. It should be noted that $r = 0.42$ because of the definition used here, $42\%$ of the encoded bits are redundant. With the reference value „bit rate of the uncoded sequence” we would get $r = 9.4/13 \approx 0.72$ with the statement: To the information bits are added $72\%$ check bits. <br> |
| − | * | + | *For [[Examples_of_Communication_Systems/Allgemeine_Beschreibung_von_UMTS|UMTS]] (<i>Universal Mobile Telecommunications System</i>), [[Channel_Coding/Grundlagen_der_Faltungscodierung|Convolutional Codes]] with the rates $R = 1/2$ or $R = 1/3$ are used. In the UMTS–modes for higher data rates and correspondingly lower spreading factors, on the other hand, one uses [[Channel_Coding/Grundlegendes_zu_den_Turbocodes|Turbo–Codes]] of the rate $R = 1/3$ and iterative decoding. Depending on the number of iterations, gains of up to $3 \, \rm dB$ can be achieved compared to convolutional coding.}}<br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 7: Error Protection of the Compact Disc}$ |
| − | <br> | + | <br>For a CD (<i>Compact Disc</i>), one uses <i>cross–interleaved</i> [[Channel_Coding/Definition_und_Eigenschaften_von_Reed–Solomon–Codes|Reed–Solomon–Codes]] (RS) and then a so-called [https://en.wikipedia.org/wiki/Eight-to-fourteen_modulation Eight–to–Fourteen–Modulation]. Redundancy is used for error detection and correction. This coding scheme shows the following characteristics: |
| − | * | + | *The common code rate of the two RS–component codes is $R_{\rm RS} = 24/28 · 28/32 = 3/4$. Through the 8–to–14–modulation and some control bits, one arrives at the total code rate $R ≈ 1/3$.<br> |
| − | * | + | *In the case of statistically independent errors according to the [[Channel_Coding/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC|BSC–model]] (<i>Binary Symmetric Channel</i> ),a complete correction is possible as long as the bit error rate does not exceed the value $10^{-3}$ .<br> |
| − | * | + | *The CD–specific <i>Cross Interleaver</i> scrambles $108$ blocks together so that the $588$ bits of a block $($each bit corresponds to approx. $0.28 \, \rm {µ m})$ are distributed over approximately $1.75\, \rm cm$.<br> |
| − | * | + | *With the code rate $R ≈ 1/3$ one can correct approx. $10\%$ „Erasures”. The lost values can be reconstructed (approximately) by interpolation ⇒ <i>Error concealment</i>.<br><br> |
| − | + | In summary, if a CD has a scratch of $1. 75\, \rm mm$ in length in the direction of play (i.e. more than $6000$ consecutive erasures), still $90\%$ of all the bits in a block are error-free, so that even the missing $10\%$ can be reconstructed, or at least the erasures can be disguised so that they are not audible.<br>. | |
| − | + | A demonstration of the CD's ability to correct follows on the next page}}<br>. | |
| − | == | + | == The "Slotted CD" - A Demonstration By The LNT of TUM == |
<br> | <br> | ||
| − | Ende der 1990er Jahre haben Mitarbeiter des [https://www.lnt.ei.tum.de/startseite/ | + | Ende der 1990er Jahre haben Mitarbeiter des [https://www.lnt.ei.tum.de/startseite/ Chair of Communications Engineering] der [https://www.tum.de/die-tum/ TU München] unter Leitung von Professor [[Biographies_and_Bibliographies/Lehrstuhlinhaber_des_LNT#Prof._Dr.-Ing._Dr.-Ing._E.h._Joachim_Hagenauer_.281993-2006.29|Joachim Hagenauer]] eine Musik–CD gezielt beschädigt, indem insgesamt drei Schlitze von jeweils mehr als einem Millimeter Breite eingefräst wurden. Damit fehlen bei jedem Defekt fast $4000$ fortlaufende Bit der Audiocodierung.<br> |
[[File:P ID2333 KC T 1 1 S2b.png|right|frame|„Geschlitzte CD” des $\rm LNT/TUM$]] | [[File:P ID2333 KC T 1 1 S2b.png|right|frame|„Geschlitzte CD” des $\rm LNT/TUM$]] | ||
Revision as of 19:41, 15 January 2021
- [[Channel Coding/{{{Vorherige Seite}}} | Previous page]]
- [[Channel Coding/{{{Vorherige Seite}}} | Previous page]]
Contents
- 1 # Overview on The First Main Chapter #
- 2 Error Detection and Error Correction
- 3 Some Introductory Examples of Error Detection
- 4 Some Introductory Examples of Error Correction
- 5 The "Slotted CD" - A Demonstration By The LNT of TUM
- 6 Zusammenspiel zwischen Quellen– und Kanalcodierung
- 7 Blockschaltbild und Voraussetzungen
- 8 Einige wichtige Definitionen zur Blockcodierung
- 9 Beispiele für Fehlererkennung und Fehlerkorrektur
- 10 Zur Nomenklatur in diesem Buch
- 11 Aufgaben zum Kapitel
- 12 Quellenverzeichnis
# Overview on The First Main Chapter #
The first chapter deals with block codes for error detection and error correction and provides the basics for describing more effective codes such as the Reed-Solomon codes (see Chapter 2), the convolutional codes (Chapter 3), and the iteratively decodable product codes (turbo codes) and low-density parity-check codes (Chapter 4). We restrict ourselves here to binary codes.
This specific field is called channel coding in contrast to source coding (redundancy reduction for reasons of data compression) and to line coding (additional redundancy to adapt the digital signal to the spectral characteristics of the transmission medium).
In detail, it covers:
- Definitions and introductory examples of error detection and error correction,
- a brief review of appropriate channel models and decision maker structures,
- known binary block codes such as single parity-check code, repetition code and Hamming code,
- the general description of linear codes using generator matrix and check matrix,
- the decoding possibilities for block codes, including syndrome decoding,
- simple approximations and upper bounds for block error probability, and
- an information-theoretic bound on channel coding.
Error Detection and Error Correction
Transmission errors occur in every message transmission system. It is possible to keep the probability $p_{\rm S}$ of such a symbol error very small, for example by using a very large signal energy. However, the symbol error probability $p_{\rm S} = 0$ is never achievable because of the Gaussian WDF of the thermal noise that is always present.
Particularly in the case of heavily disturbed channels and also for safety-critical applications, it is therefore essential to provide special protection for the data to be transmitted, adapted to the application and channel. For this purpose, redundancy is added at the transmitter and this redundancy is used at the receiver to reduce the number of decoding errors.
$\text{Definitions:}$
- Error Detection : The decoder checks the integrity of the received blocks and marks any errors found. If necessary, the receiver informs the transmitter about erroneous blocks via the return channel, so that the transmitter sends the corresponding block again.
- Error Correction The decoder detects one (or more) bit errors and provides further information for them, for example their positions in the transmitted block. In this way, it may be possible to completely correct the errors that have occurred.
- The Channel Coding includes procedures for error detection as well as those for error correction.
All ARQ (Automatic Repeat Request) procedures use error detection only. Less redundancy is required for error detection than for error correction. One disadvantage of ARQ is its low throughput when channel quality is poor, i.e. when entire blocks of data must be frequently re-requested by the receiver.
In this book we mostly deal with Forward Error Correction which leads to very small error rates if the channel is sufficiently good (large SNR). With worse channel conditions, nothing changes in the throughput, i.e. the same amount of information is transmitted. However, the error rate can then assume very large values.
Often FEC and ARQ methods are combined, and the redundancy is divided between them in such a way,
- so that a small number of errors can still be corrected,
but *when there are many errors, a repeat of the block is requested.
Some Introductory Examples of Error Detection
$\text{Example 1: Single Parity–Check Code (SPC)}$
If one adds $k = 4$ bit by a so-called check bit (English: Parity Bit ) in such a way that the sum of all ones is even, for example (with bold check bits)
- $$0000\boldsymbol{0}, 0001\boldsymbol{1}, \text{...} , 1111\boldsymbol{0}, \text{...}\ ,$$
it is very easy to recognise a single error. Two errors within a code word, on the other hand, remain undetected.
$\text{Example 2: International Standard Book Number (ISBN)}$
Since the 1960s, all books have been given 10-digit codes (ISBN–10 ). Since 2007, the specification according to ISBN–13 is additionally obligatory. For example, these are for the reference book [Söd93][1]:
- $\boldsymbol{3–540–57215–5}$ (for ISBN–10), bzw.
- $\boldsymbol{978–3–54057215–2}$ (for ISBN–13).
The last digit $z_{10}$ for ISBN–10 results from the previous digits $z_1 = 3$, $z_2 = 5$, ... , $z_9 = 5$ according to the following calculation rule:
- \[z_{10} = \left ( \sum_{i=1}^{9} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.3cm} \mod 11 = (1 \cdot 3 + 2 \cdot 5 + ... + 9 \cdot 5 ) \hspace{-0.2cm} \mod 11 = 5 \hspace{0.05cm}. \]
Note that $z_{10} = 10$ must be written as $z_{10} = \rm X$ (Roman numeral representation of „10”), since the number $10$ cannot be represented as a digit in the decimal system.
The same applies to the check digit for ISBN–13:
- \[z_{13}= 10 - \left ( \sum_{i=1}^{12} \hspace{0.2cm} z_i \cdot 3^{(i+1) \hspace{-0.2cm} \mod 2} \right ) \hspace{-0.3cm} \mod 10 = 10 \hspace{-0.05cm}- \hspace{-0.05cm} \big [(9\hspace{-0.05cm}+\hspace{-0.05cm}8\hspace{-0.05cm}+\hspace{-0.05cm}5\hspace{-0.05cm}+\hspace{-0.05cm}0\hspace{-0.05cm}+\hspace{-0.05cm}7\hspace{-0.05cm}+\hspace{-0.05cm}1) \cdot 1 + (7\hspace{-0.05cm}+\hspace{-0.05cm}3\hspace{-0.05cm}+\hspace{-0.05cm}4\hspace{-0.05cm}+\hspace{-0.05cm}5\hspace{-0.05cm}+\hspace{-0.05cm}2\hspace{-0.05cm}+\hspace{-0.05cm}5) \cdot 3\big ] \hspace{-0.2cm} \mod 10 \]
- \[\Rightarrow \hspace{0.3cm} z_{13}= 10 - (108 \hspace{-0.2cm} \mod 10) = 10 - 8 = 2 \hspace{0.05cm}. \]
With both variants, in contrast to the above parity check code (SPC), number twists such as $57 \, \leftrightarrow 75$ are also recognised, since different positions are weighted differently here
.
$\text{Example 3: Barcode (one-dimensional)}$
The most widely used error-detecting code worldwide is the bar code or bar code (English: Bar Code) for marking products, for example according to EAN–13 (European Article Number ) with 13 digits.
- These are represented by bars and gaps of different widths and can be easily decoded with an opto–cial reader.
- The first three digits indicate the country (for example Germany: between 400 and 440), the next four or five digits the manufacturer and the product.
- The last digit is the check digit $z_{13}$, which is calculated exactly as for ISBN–13.
Some Introductory Examples of Error Correction
$\text{Example 4: 2D–Barcodes For Online–Tickets}$
If you book a Deutsche Bahn ticket online and print it out, you will find an example of a two-dimensional barcode, namely the Aztec–Code developed in 1995 by Andy Longacre at the Welch Allyn company in the USA, with which amounts of data up to $3000$ characters can be encoded. Due to the Reed–Solomon–error correction reconstruction of the data content is still possible even if up to $40\%$ of the code has been destroyed, for example by bending the ticket or by coffee stains.
On the right is a $\rm QR–Code$ (Quick Response) with associated content. The QR–code was developed in 1994 for the automotive industry in Japan to mark components and also allows error correction. In the meantime, the use of the QR–code has become very diverse. In Japan, it can be found on almost every advertising poster and on every business card. It is also becoming more and more popular in Germany.
All 2D–barcodes have square markings to calibrate the reader. You can find details on this in [KM+09][2].
$\text{Example 5: Codes For Satellites– And Space Communications}$
One of the first areas of application of error correction methods was communication from/to satellites and space shuttles, i.e. transmission routes characterised by low transmission powers and large path losses. As early as 1977, channel coding was used in the space–mission Voyager 1 to Neptune and Uranus, in the form of serial concatenation of a Reed–Solomon–Code and a convolutional code.
Thus, the power parameter $10 · \lg \; E_{\rm B}/N_0 \approx 2 \, \rm dB$ was already sufficient to achieve the required error rate $5 · 10^{-5}$ (related to the compressed data after source coding). Without channel coding, on the other hand, almost $9 \, \rm dB$ are required for the same error rate, i.e. a factor $10^{0.7} ≈ 5$ greater transmission power.
The planned Mars project (data transmission from Mars to Earth with $\rm 5W$–lasers) will also only be successful with a sophisticated coding scheme
.
$\text{Example 6: Channel Codes For Mobile Communikations}$
A further and particularly high-turnover application area that would not function without channel coding is mobile communication. Here, unfavourable conditions without coding would result in error rates in the percentage range and, due to shadowing and multipath propagation (echoes), the errors often occur in bundles. The error bundle length is sometimes several hundred bits.
- For voice transmission in the GSM–system, the $182$ most important (class 1a and 1b) of the total 260 bits of a voice frame $(20 \, \rm ms)$ together with a few parity– and tailbits are convolutionally coded $($with memory $m = 4$ and rate $R = 1/2)$ and scrambled. Together with the $78$ less important and therefore uncoded bits of class 2, this results in the bit rate increasing from $13 \, \rm kbit/s$ to $22.4 \, \rm kbit/s$ .
- One uses the (relative) redundancy of $r = (22.4 - 13)/22.4 ≈ 0.42$ for error correction. It should be noted that $r = 0.42$ because of the definition used here, $42\%$ of the encoded bits are redundant. With the reference value „bit rate of the uncoded sequence” we would get $r = 9.4/13 \approx 0.72$ with the statement: To the information bits are added $72\%$ check bits.
- For UMTS (Universal Mobile Telecommunications System), Convolutional Codes with the rates $R = 1/2$ or $R = 1/3$ are used. In the UMTS–modes for higher data rates and correspondingly lower spreading factors, on the other hand, one uses Turbo–Codes of the rate $R = 1/3$ and iterative decoding. Depending on the number of iterations, gains of up to $3 \, \rm dB$ can be achieved compared to convolutional coding.
$\text{Example 7: Error Protection of the Compact Disc}$
For a CD (Compact Disc), one uses cross–interleaved Reed–Solomon–Codes (RS) and then a so-called Eight–to–Fourteen–Modulation. Redundancy is used for error detection and correction. This coding scheme shows the following characteristics:
- The common code rate of the two RS–component codes is $R_{\rm RS} = 24/28 · 28/32 = 3/4$. Through the 8–to–14–modulation and some control bits, one arrives at the total code rate $R ≈ 1/3$.
- In the case of statistically independent errors according to the BSC–model (Binary Symmetric Channel ),a complete correction is possible as long as the bit error rate does not exceed the value $10^{-3}$ .
- The CD–specific Cross Interleaver scrambles $108$ blocks together so that the $588$ bits of a block $($each bit corresponds to approx. $0.28 \, \rm {µ m})$ are distributed over approximately $1.75\, \rm cm$.
- With the code rate $R ≈ 1/3$ one can correct approx. $10\%$ „Erasures”. The lost values can be reconstructed (approximately) by interpolation ⇒ Error concealment.
In summary, if a CD has a scratch of $1. 75\, \rm mm$ in length in the direction of play (i.e. more than $6000$ consecutive erasures), still $90\%$ of all the bits in a block are error-free, so that even the missing $10\%$ can be reconstructed, or at least the erasures can be disguised so that they are not audible.
.
A demonstration of the CD's ability to correct follows on the next page
.
The "Slotted CD" - A Demonstration By The LNT of TUM
Ende der 1990er Jahre haben Mitarbeiter des Chair of Communications Engineering der TU München unter Leitung von Professor Joachim Hagenauer eine Musik–CD gezielt beschädigt, indem insgesamt drei Schlitze von jeweils mehr als einem Millimeter Breite eingefräst wurden. Damit fehlen bei jedem Defekt fast $4000$ fortlaufende Bit der Audiocodierung.
Die Grafik zeigt die „geschlitzte CD”:
- Sowohl in der Spur 3 als auch in der Spur 14 gibt es bei jeder Umdrehung zwei solcher fehlerhafter Bereiche.
- Sie können sich die Musikqualität mit Hilfe der beiden Audioplayer (Abspielzeit jeweils ca. 15 Sekunden) verdeutlichen.
- Die Theorie zu dieser Audio–Demo finden Sie im $\text{Beispiel 7}$ auf der vorherigen Seite.
Spur 14:
Spur 3:
Resumee dieser Audiodemo:
- Die Fehlerkorrektur der CD basiert auf zwei seriell–verketteten Reed–Solomon–Codes sowie einer Eight–to–Fourteen–Modulation. Die Gesamtcoderate zur RS–Fehlerkorrektur beträgt $R = 3/4$.
- Ebenso wichtig für die Funktionsfähigkeit der CD wie die Codes ist der dazwischen geschaltete Interleaver, der die ausgelöschten Bits („Erasures”) über eine Länge von fast $2 \, \rm cm$ verteilt.
- Bei der Spur 14 liegen die beiden defekten Bereiche genügend weit auseinander. Deshalb ist der Reed–Solomon–Decoder in der Lage, die fehlenden Daten zu rekonstruieren.
- Bei der Spur 3 folgen die beiden Fehlerblöcke in sehr kurzem Abstand aufeinander, so dass der Korrekturalgorithmus versagt. Das Resultat ist ein fast periodisches Klackgeräusch.
Wir bedanken uns bei Rainer Bauer, Thomas Hindelang und Manfred Jürgens, diese Audio–Demo verwenden zu dürfen.
Zusammenspiel zwischen Quellen– und Kanalcodierung
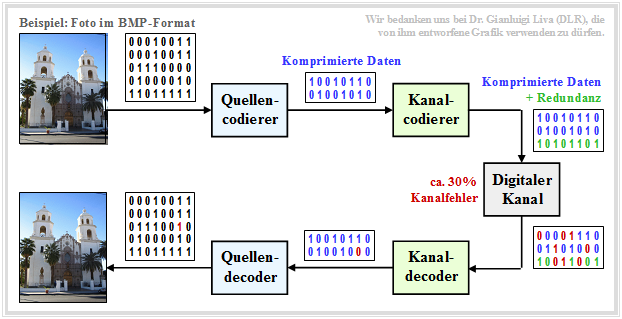
Die Nachrichtenübertragung natürlicher Quellen wie Sprache, Musik, Bilder, Videos, usw. geschieht meist entsprechend dem nachfolgend skizzierten zeitdiskreten Modell.
Zu dieser aus [Liv10][3] entnommenen Grafik ist Folgendes anzumerken:
- Quelle und Sinke sind digitalisiert und werden durch (etwa gleich viele ) Nullen und Einsen repräsentiert.
- Der Quellencodierer komprimiert die binären Daten – im Beispiel ein Digitalfoto – und reduziert somit die Redundanz der Quelle.
- Der Kanalcodierer fügt wieder Redundanz hinzu und zwar gezielt, so dass einige der auf dem Kanal entstandenen Fehler im Kanaldecoder korrigiert werden können.
- Für den Kanal wird hier ein zeitdiskretes Modell mit binärem Eingang und Ausgang verwendet, das auch die Komponenten der technischen Sende– und Empfangseinrichtungen (Modulator, Entscheider, Taktwiedergewinnung) geeignet berücksichtigen sollte.
Bei richtiger Dimensionierung von Quellen– und Kanalcodierung ist die Qualität des empfangenen Fotos hinreichend gut, auch wenn die Sinkensymbolfolge aufgrund nicht korrigierbarer Fehlermuster nicht exakt mit der Quellensymbolfolge übereinstimmen wird. Man erkennt innerhalb der Sinkensymbolfolge einen (rot markierten) Bitfehler.
$\text{Beispiel 8:}$ Für obige Grafik wurde beispielhaft und stark vereinfachend angenommen, dass
- die Quellensymbolfolge nur die Länge $40$ hat,
- der Quellencodierer die Daten um den Faktor $40/16 = 2.5$ komprimiert, und
- der Kanalcoder $50\%$ Redundanz hinzufügt.
Übertragen werden müssen also nur $24$ Codersymbole statt $40$ Quellensymbole, was die Übertragungsrate insgesamt um $40\%$ reduziert.
Würde man auf die Quellencodierung verzichten, in dem man das ursprüngliche Foto im BMP–Format übertragen würde und nicht das komprimierte JPG–Bild, so wäre die Qualität vergleichbar, aber eine um den Faktor $2.5$ höhere Bitrate und damit sehr viel mehr Aufwand erforderlich.
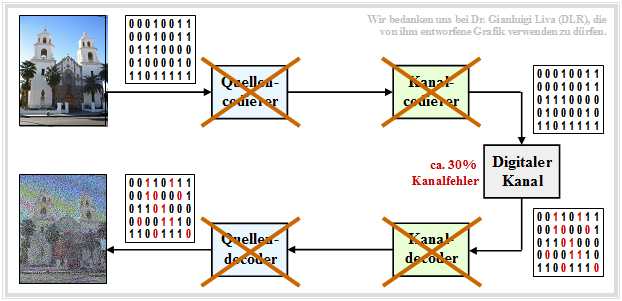
$\text{Beispiel 9:}$ Würde man sowohl auf die Quellen– als auch auf die Kanalcodierung verzichten, also direkt die BMP–Daten ohne Fehlerschutz übertragen, so wäre das Ergebnis trotz $($um den Faktor $40/24)$ größerer Bitrate äußerst dürftig.
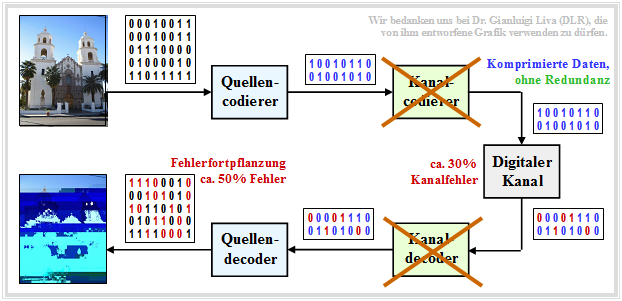
$\text{Beispiel 10:}$ Nun betrachten wir den Fall, dass man die komprimierten Daten (zum Beispiel JPG) ohne Fehlersicherungsmaßnahmen direkt überträgt.
- Da die komprimierte Quelle nur noch wenig Redundanz besitzt, führt jeder einzelne Übertragungsfehler dazu, dass ganze Bildblöcke falsch decodiert werden.
- Dieses Codierschema (Quellencodierung, aber keine Kanalcodierung) sollte auf jeden Fall vermieden werden.
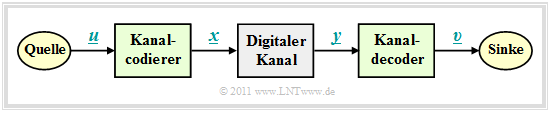
Blockschaltbild und Voraussetzungen
Im weiteren Verlauf gehen wir von dem skizzierten Blockschaltbild mit Kanalcodierer, Digitalem Kanal und Kanaldecoder aus.
Dabei gelten folgende Voraussetzungen:
- Der Vektor $\underline{u} = (u_1, u_2, \text{...} \hspace{0.05cm}, u_k)$ kennzeichnet einen Informationsblock mit $k$ Symbolen.
- Meist beschränken wir uns auf Binärsymbole (Bits) ⇒ $u_i \in \{0, \, 1\}$ für $i = 1, 2, \text{...} \hspace{0.05cm}, k$ mit gleichen Auftrittswahrscheinlichkeiten für Nullen und Einsen.
- Jeder Informationsblock $\underline{u}$ wird durch ein Codewort (oder einen Codeblock) $\underline{x} = (x_1, x_2, \text{...} \hspace{0.05cm}, x_n)$ mit $n \ge k$, $x_i \in \{0, \, 1\}$ dargestellt. Man spricht dann von einem binären $(n, k)$–Blockcode $C$. Die Zuordnung bezeichnen wir mit $\underline{x} = {\rm enc}(\underline{u})$, wobei „enc” für „Encoder–Funktion” steht.
- Das Empfangswort $\underline{y}$ ergibt sich aus dem Codewort $\underline{x}$ durch Modulo–2–Addition mit dem ebenfalls binären Fehlervektor $\underline{e} = (e_1, e_2, \text{...} \hspace{0.05cm}, e_n)$, wobei „$e= 1$” für einen Übertragungfehler steht und „$e= 0$” anzeigt, dass das $i$–te Bit des Codewortes richtig übertragen wurde. Es gilt also:
- \[\underline{y} = \underline{x} \oplus \underline{e} \hspace{0.05cm}, \hspace{0.5cm} y_i = x_i \oplus e_i \hspace{0.05cm}, \hspace{0.2cm} i = 1, \text{...} \hspace{0.05cm} , n\hspace{0.05cm}, x_i \hspace{-0.05cm} \in \hspace{-0.05cm} \{ 0, 1 \}\hspace{0.05cm}, \hspace{0.5cm}e_i \in \{ 0, 1 \}\hspace{0.5cm} \Rightarrow \hspace{0.5cm}y_i \in \{ 0, 1 \}\hspace{0.05cm}.\]
- Die Beschreibung durch das Digitale Kanalmodell – also mit binärem Eingang und Ausgang – ist allerdings nur dann anwendbar, wenn das Übertragungssystem harte Entscheidungen trifft – siehe AWGN–Kanal bei binärem Eingang. Systeme mit Soft Decision sind mit diesem einfachen Modell nicht modellierbar.
- Der Vektor $\underline{v}$ nach der Kanaldecodierung hat die gleiche Länge $k$ wie der Informationsblock $\underline{u}$. Den Decodiervorgang beschreiben wir mit der „Decoder–Funktion” als $\underline{v} = {\rm enc}^{-1}(\underline{y}) = {\rm dec}(\underline{y})$. Im fehlerfreien Fall gilt analog zu $\underline{x} = {\rm enc}(\underline{u})$ auch $\underline{v} = {\rm enc}^{-1}(\underline{y})$.
- Ist der Fehlervektor $\underline{e} \ne \underline{0}$, so ist $\underline{y}$ meist kein gültiges Element des verwendeten Blockcodes, und die Decodierung ist dann keine reine Zuordnung $\underline{y} \rightarrow \underline{v}$, sondern eine auf maximale Übereinstimmung (mimimale Fehlerwahrscheinlichkeit) basierende Schätzung von $\underline{v}$.
Einige wichtige Definitionen zur Blockcodierung
Wir betrachten nun den beispielhaften binären Blockcode
\[\mathcal{C} = \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 0, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 1, 1) \}\hspace{0.05cm}.\]
Dieser Code wäre zum Zwecke der Fehlererkennung oder –korrektur ungeeignet. Aber er ist so konstruiert, dass er die Berechnung wichtiger Beschreibungsgrößen anschaulich verdeutlicht:
- Jedes einzelne Codewort $\underline{u}$ wird durch fünf Bit beschrieben. Im gesamten Buch drücken wir diesen Sachverhalt durch die Codewortlänge (englisch: Code Length ) $n = 5$ aus.
- Der obige Code beinhaltet vier Elemente. Damit ist der Codeumfang (englisch: Size ) $|C| = 4$. Entsprechend gibt es auch vier eindeutige Zuordnungen (englisch: Mappings ) zwischen $\underline{u}$ und $\underline{x}$.
- Die Länge eines Informationsblocks $\underline{u}$ ⇒ Informationsblocklänge wird mit $k$ bezeichnet. Da bei allen binären Codes $|C| = 2^k$ gilt, folgt aus $|C| = 4$ der Wert $k = 2$. Die Zuordnungen zwischen $\underline{u}$ und $\underline{x}$ lauten bei obigem Code $C$:
- \[\underline{u_0} = (0, 0) \hspace{0.2cm}\leftrightarrow \hspace{0.2cm}(0, 0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm}, \hspace{0.8cm} \underline{u_1} = (0, 1) \hspace{0.2cm}\leftrightarrow \hspace{0.2cm}(0, 1, 0, 1, 0) = \underline{x_1}\hspace{0.05cm}, \]
- \[\underline{u_2} = (1, 0)\hspace{0.2cm} \leftrightarrow \hspace{0.2cm}(1, 0, 1, 0, 1) = \underline{x_2}\hspace{0.05cm}, \hspace{0.8cm} \underline{u_3} = (1, 1) \hspace{0.2cm} \leftrightarrow \hspace{0.2cm}(1, 1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.\]
- Der Code weist die Coderate $R = k/n = 2/5$ auf. Dementsprechend beträgt seine Redundanz $1-R$, also $60\%$. Ohne Fehlerschutz $($also für den Fall $n = k)$ wäre die Coderate $R = 1$.
- Eine kleine Coderate zeigt an, dass von den $n$ Bits eines Codewortes nur sehr wenige tatsächlich Information tragen. Beispielsweise hat ein Wiederholungscode $(k = 1)$ mit $n = 10$ die Coderate $R = 0.1$.
- Das Hamming–Gewicht $w_{\rm H}(\underline{x})$ des Codewortes $\underline{x}$ gibt die Zahl der Codewortelemente $x_i \ne 0$ an. Bei einem binären Code ⇒ $x_i \in \{0, \, 1\}$ ist $w_{\rm H}(\underline{x})$ gleich der Summe $x_1 + x_2 + \hspace{0.05cm}\text{...} \hspace{0.05cm}+ x_n$. Im Beispiel:
- \[w_{\rm H}(\underline{x}_0) = 0\hspace{0.05cm}, \hspace{0.4cm}w_{\rm H}(\underline{x}_1) = 2\hspace{0.05cm}, \hspace{0.4cm} w_{\rm H}(\underline{x}_2) = 3\hspace{0.05cm}, \hspace{0.4cm}w_{\rm H}(\underline{x}_3) = 5\hspace{0.05cm}. \]
- Die Hamming–Distanz $d_{\rm H}(\underline{x}, \ \underline{x}\hspace{0.03cm}')$ zwischen den Codeworten $\underline{x}$ und $\underline{x}\hspace{0.03cm}'$ bezeichnet die Anzahl der Bitpositionen, in denen sich die beiden Codeworte unterscheiden:
- \[d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_1) = 2\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_2) = 3\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_3) = 5\hspace{0.05cm},\hspace{0.4cm} d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_2) = 5\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_3) = 3\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_2, \hspace{0.05cm}\underline{x}_3) = 2\hspace{0.05cm}.\]
- Eine wichtige Eigenschaft eines Codes $C$, die seine Korrekturfähigkeit wesentlich beeinflusst, ist die minimale Distanz zwischen zwei beliebigen Codeworten:
- \[d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}')\hspace{0.05cm}.\]
$\text{Definition:}$ Ein $(n, \hspace{0.05cm}k, \hspace{0.05cm}d_{\rm min})\text{ – Blockcode}$ besitzt die Codewortlänge $n$, die Informationsblocklänge $k$ und die minimale Distanz $d_{\rm min}$.
- Nach dieser Nomenklatur handelt es sich im hier betrachteten Beispiel um einen $(5, \hspace{0.05cm}2,\hspace{0.05cm} 2)$ – Blockcode.
- Manchmal verzichtet man auf die Angabe von $d_{\rm min}$ und spricht dann von einem $(n,\hspace{0.05cm} k)$ – Blockcode.
Beispiele für Fehlererkennung und Fehlerkorrektur
Die eben definierten Größen sollen nun an zwei Beispielen verdeutlicht werden.
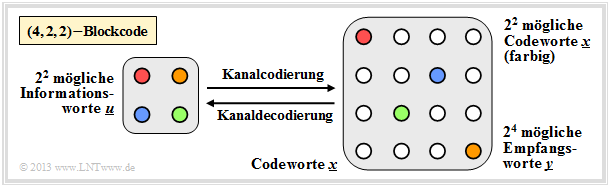
$\text{Beispiel 11:}$ $\text{(4, 2, 2)–Blockcode}$
In der Grafik verdeutlichen die nach rechts bzw. links zeigenden Pfeile den Codiervorgang bzw. die Decodierung:
- $$\underline{u_0} = (0, 0) \leftrightarrow (0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm},\hspace{0.5cm} \underline{u_1} = (0, 1) \leftrightarrow (0, 1, 0, 1) = \underline{x_1}\hspace{0.05cm},$$
- $$\underline{u_2} = (1, 0) \leftrightarrow (1, 0, 1, 0) = \underline{x_2}\hspace{0.05cm},\hspace{0.5cm} \underline{u_3} = (1, 1) \leftrightarrow (1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.$$
Rechts sind alle $2^4 = 16$ möglichen Empfangsworte $\underline{y}$ dargestellt:
- Von diesen können $2^n - 2^k = 12$ nur durch Bitfehler entstanden sein.
- Empfängt der Decoder ein solches „weißes” Codewort, so erkennt er zwar einen Fehler, er kann diesen aber wegen $d_{\rm min} = 2$ nicht korrigieren.
- Empfängt er beispielsweise $\underline{y} = (0, 0, 0, 1)$, so kann nämlich mit gleicher Wahrscheinlichkeit $\underline{x_0} = (0, 0, 0, 0)$ oder $\underline{x_1} = (0, 1, 0, 1)$ gesendet worden sein.
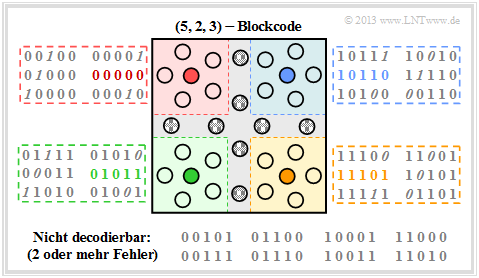
$\text{Beispiel 11:}$ $\text{(5, 2, 3)–Blockcode}$
Hier gibt es wegen $k=2$ vier gültige Codeworte :
- $$\underline{x_0} = (0, 0, 0, 0, 0)\hspace{0.05cm},\hspace{0.5cm} \underline{x_1} =(0, 1, 0, 1, 1)\hspace{0.05cm},$$
- $$\underline{x_2} =(1, 0, 1, 1, 0)\hspace{0.05cm},\hspace{0.5cm}\underline{x_3} =(1, 1, 1, 0, 1).$$
In der Grafik dargestellt ist die Empfängerseite, wobei man verfälschte Bit an der Kursivschrift erkennt.
- Von den $2^n - 2^k = 28$ unzulässigen Codeworten lassen sich nun $20$ einem gültigen Codewort (Füllfarbe: rot, grün, blau oder ocker) zuordnen, wenn man davon ausgeht, dass ein einziger Bitfehler wahrscheinlicher ist als deren zwei oder mehr.
- Zu jedem gültigen Codewort gibt es fünf unzulässige Codeworte mit jeweils nur einer Verfälschung ⇒ Hamming–Distanz $d_{\rm H} =1$. Diese sind in dem jeweiligen Quadrat mit roter, grüner, blauer oder ockerfarbenen Hintergrundfarbe angegeben.
- Die Fehlerkorrektur ist für diese aufgrund der minimalen Distanz $d_{\rm min} = 3$ zwischen den Codeworten möglich.
- Acht Empfangsworte sind nicht decodierbar. Beispielsweise könnte das Empfangswort $\underline{y} = (0, 0, 1, 0, 1)$ aus dem Codewort $\underline{x}_0 = (0, 0, 0, 0, 0)$ entstanden sein, aber auch aus dem Codewort $\underline{x}_3 = (1, 1, 1, 0, 1)$. In beiden Fällen wären zwei Bitfehler aufgetreten.
Zur Nomenklatur in diesem Buch
Eine Zielvorgabe unseres Lerntutorials $\rm LNTwww$ war, das gesamte Fachgebiet der Nachrichtentechnik und der zugehörigen Grundlagenfächer mit einheitlicher Nomenklatur zu beschreiben. In diesem zuletzt in Angriff genommenen Buch „ Kanalcodierung” müssen nun doch einige Änderungen hinsichtlich der Nomenklatur vorgenommen werden. Die Gründe hierfür sind:
- Die Codierungstheorie ist ein weitgehend in sich abgeschlossenes Fachgebiet und nur wenige Autoren von einschlägigen Fachbüchern zu diesem Gebiet versuchen, einen Zusammenhang mit anderen Aspekten der Digitalsignalübertragung herzustellen.
- Die Autoren der wichtigsten Bücher zur Kanalcodierung – englischsprachige und deutsche – verwenden weitgehend eine einheitliche Nomenklatur. Wir erlauben uns deshalb nicht, die Bezeichnungen zur Kanalcodierung in unser Übertragungstechnik–Schema zu pressen.
Einige Nomenklaturänderungen gegenüber den anderen $\rm LNTwww$–Büchern sollen hier genannt werden:
- Alle Signale werden durch Symbolfolgen in Vektorschreibweise dargestellt. Beispielsweise kennzeichnet $\underline{u} = (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$ die Quellensymbolfolge und $\underline{v} = (v_1, v_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, v_k)$ die Sinkensymbolfolge. Bisher wurden diese Symbolfolgen mit $\langle q_\nu \rangle$ bzw. $\langle v_\nu \rangle$ bezeichnet.
- Der Vektor $\underline{x} = (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n)$ bezeichnet nun das zeitdiskrete Äquivalent zum Sendesignal $s(t)$, während das Empfangssignal $r(t)$ durch den Vektor $\underline{y} = (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$ beschrieben wird. Die Coderate ist der Quotient $R=k/n$ mit $0 \le R \le 1$ und die Anzahl der Prüfbits ergibt sich zu $m = n-k$.
- Im ersten Hauptkapitel sind die Elemente $u_i$ und $v_i$ $($jeweils mit Index $i = 1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, k)$ der Vektoren $\underline{u}$ und $\underline{v}$ stets binär $(0$ oder $1)$, ebenso wie die $n$ Elemente $x_i$ des Codewortes $\underline{x}$. Bei digitalem Kanalmodell (BSC, BEC, BSEC) gilt auch für die $n$ Empfangswerte $y_i \in \{0, 1\}$.
- Das AWGN–Kanalmodell ist durch reellwertige Ausgangswerte $y_i$ gekennzeichnet. Der Codewortschätzer gewinnt in diesem Fall aus dem Vektor $\underline{y} = (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$ den binären Vektor $\underline{z} = (z_1, z_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, z_n)$, der mit dem Codewort $\underline{x}$ zu vergleichen ist.
- Der Übergang von $\underline{y}$ auf $\underline{z}$ erfolgt durch Schwellenwertentscheidung ⇒ Hard Decision oder nach dem MAP–Kriterium ⇒ Soft Decision. Bei gleichwahrscheinlichen Eingangssymbolen führt die „Maximum Likelihood”–Schätzung ebenfalls zur minimalen Fehlerrate.
- Im Zusammenhang mit dem AWGN–Modell macht es Sinn, binäre Codesymbole $x_i$ bipolar (also $\pm1$) darzustellen. An den statistischen Eigenschaften ändert sich dadurch nichts. Wir kennzeichnen im Folgenden die bipolare Signalisierung durch eine Tilde. Dann gilt:
- \[\tilde{x}_i = 1 - 2 x_i = \left\{ \begin{array}{c} +1\\ -1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls} \hspace{0.15cm} x_i = 0\hspace{0.05cm},\\ {\rm falls} \hspace{0.15cm}x_i = 1\hspace{0.05cm}.\\ \end{array}\]
Aufgaben zum Kapitel
Aufgabe 1.1: Zur Kennzeichnung aller Bücher
Aufgabe 1.2: Einfacher binärer Kanalcode
Aufgabe 1.2Z: 3D–Darstellung von Codes
Quellenverzeichnis
- ↑ Söder, G.: Modellierung, Simulation und Optimierung von Nachrichtensystemen. Berlin - Heidelberg: Springer, 1993.
- ↑ Kötter, R.; Mayer, T.; Tüchler, M.; Schreckenbach, F.; Brauchle, J.: Channel Coding. Lecture Notes, Lehrstuhl für Nachrichtentechnik, TU München, 2008.
- ↑ Liva, G.: Channel Coding. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2010.