Difference between revisions of "Aufgaben:Exercise 3.12: Strictly Symmetrical Channels"
| (23 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Application_to_Digital_Signal_Transmission |
}} | }} | ||
| − | [[File: | + | [[File:EN_Inf_A_3_11.png|right|frame|Predefined sub-channel model (top) <br>and BSEC model (bottom)]] |
| − | + | The upper diagram shows two strictly symmetric subchannels $\rm A$ and $\rm B$. | |
| − | + | *A '''strongly symmetric channel''' is one that is "uniformly dispersive" ⇒ each input symbol $u$ has the same set of transition probabilities: | |
| − | $$\left \{ P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.02cm}U}(y\hspace{ | + | :$$\left \{ P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.02cm}U}(y\hspace{0.03cm} |\hspace{0.03cm} u) \hspace{-0.05cm}: \hspace{0.25cm}u \in U \right \} \hspace{0.05cm},$$ |
| − | + | * moreover, '''uniformly focusing''' ⇒ each output symbol $y$ has the same set of transition probabilities: | |
| − | $$ \left \{ P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.02cm}U}(y\hspace{ | + | :$$ \left \{ P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.02cm}U}(y\hspace{0.03cm} |\hspace{0.03cm} u) \hspace{-0.05cm}: \hspace{0.25cm}y \in Y \right \} \hspace{0.05cm}.$$ |
| − | + | The random quantity $U = \{0,\ 1\}$ occurs directly at the inputs of the sub-channels $\rm A$ and $\rm B$. | |
| − | + | The channel capacity of a strictly symmetrical channel can be calculated much more easily than in the asymmetrical case. However, this will not be discussed in detail in this exercise. | |
| − | + | For the capacity of the total channel applies: | |
| − | $$ C = p_{\rm A} \cdot C_{\rm A} + p_{\rm B} \cdot C_{\rm B}\hspace{0.05cm}$$ | + | :$$ C = p_{\rm A} \cdot C_{\rm A} + p_{\rm B} \cdot C_{\rm B}\hspace{0.05cm}$$ |
| − | + | Here $p_{\rm A}$ denotes the probability that the sub-channel $\rm A$ is selected and $C_{\rm A}$ indicates its capacity. The same applies to sub-channel $\rm B$. | |
| − | + | Subsequently, the channel capacity of the [[Channel_Coding/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Error_.26_Erasure_Channel_.E2.80.93_BSEC|Binary Symmetric Error & Erasure Channel]] $\rm (BSEC)$ is also to be determined according to the sketch below (grey background) by deriving the relationship between | |
| − | + | *the parameters $p_{\rm A}$, $p_{\rm B}$ and the crossover probability $q$ of the sub-channel model shown above, and | |
| − | + | * the parameters $λ$ and $\varepsilon$ of the BSEC model. | |
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung|Application to Digital Signal Transmission]]. | ||
| + | *Reference is made in particular to the page [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Properties_of_symmetrical_channels|Properties of symmetrical channels]]. | ||
| + | |||
| + | *According to [[Aufgaben:Aufgabe_3.10Z:_BSC–Kanalkapazität|Exercise 3.10Z]] , the following applies to the channel capacity of the BSC model with the crossover probability $\varepsilon$: | ||
| + | :$$ C_{\rm BSC} = 1 - H_{\rm bin}(\varepsilon)\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the capacity $C_{\rm A}$ of sub-channel $\rm A$? |
| − | |type=" | + | |type="()"} |
| − | + $ | + | + $C_{\rm A} = 1 - H_{\rm bin}(q),$ |
| − | - $ | + | - $C_{\rm A} = p_{\rm A} · \big[1 - H_{\rm bin}(q)\big],$ |
| − | - $ | + | - $C_{\rm A} = 0.$ |
| − | { | + | {What is the capacity $C_{\rm B}$ of sub-channel $\rm B$? |
| − | |type=" | + | |type="()"} |
| − | - $ | + | - $C_{\rm B} = 1 - H_{\rm bin}(q),$ |
| − | - $ | + | - $C_{\rm B} = p_{\rm B} · \big[1 - H_{\rm bin}(q)\big],$ |
| − | + $ | + | + $C_{\rm B} = 0.$ |
| − | { | + | {What is the capacity $C$ of the total channel? |
|type="[]"} | |type="[]"} | ||
| − | - $C = 1 | + | - $C = 1 - H_{\rm bin}(q),$ |
| − | + $C = | + | + $C = p_{\rm A} · \big[1 - H_{\rm bin}(q)\big],$ |
- $C = 0.$ | - $C = 0.$ | ||
| − | { | + | {How do you get from the considered sub-channel model to the BSEC model? With |
|type="[]"} | |type="[]"} | ||
| − | - $ | + | - $p_{\rm A} = λ,$ |
| − | + $ | + | + $p_{\rm A} = 1 - λ,$ |
| − | - $ | + | - $p_{\rm A} = ε$, |
| − | - $ | + | - $p_{\rm A} = ε/(1 - λ)?$ |
| − | { | + | {How do you get from the considered sub-channel model to the BSEC model? With |
|type="[]"} | |type="[]"} | ||
- $q = λ,$ | - $q = λ,$ | ||
| − | - $q = 1 | + | - $q = 1 - λ,$ |
- $q = ε,$ | - $q = ε,$ | ||
| − | + $q = ε/(1 | + | + $q = ε/(1 - λ)?$ |
| − | { | + | {What is the channel capacity of the BSEC ("Binary Symmetric Error & Erasure Channel") for $ε = 0.08$ and $λ = 0.2.$ |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $C_{\rm BSEC} \ = \ $ { 0.425 3% } $\ \rm bit$ |
| − | { | + | {What is the channel capacity of the BSC ("Binary Symmetric Channel") for $ε = 0.08$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $C_{\rm BSC}\ = \ $ { 0.598 3% } $\ \rm bit$ |
| − | { | + | {What is the channel capacity of the BEC ("Binary Erasure Channel") for $λ = 0.2$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $C_{\rm BEC}\ = \ $ { 0.8 3% } $\ \rm bit$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Subchannel $\rm A$ is a ("Binary Symmetric Channel") with crossover probability $q$ ⇒ <u>Proposed solution 1</u>. |
| + | |||
| + | |||
| + | '''(2)''' Subchannel $\rm B$ is an "erasure channel". Both the sink entropy and irrelevance of this subchannel are zero ⇒ <u>Proposed solution 3</u>. | ||
| + | |||
| + | |||
| + | [[File:EN_Inf_A_3_11e.png|right|frame|BSEC model (top) and <br>given partial channel model (down)]] | ||
| + | '''(3)''' The capacity $C$ of the total channel can be calculated using the given equation: | ||
| + | :$$ C = p_{\rm A} \cdot C_{\rm A} + p_{\rm B} \cdot C_{\rm B} = p_{\rm A} \cdot \big[1 - H_{\rm bin}(q)\big]\hspace{0.05cm}.$$ | ||
| + | Thus, the <u>proposed solution 2</u> is correct here. | ||
| + | |||
| + | |||
| + | '''(4)''' In the model considered so far, the transition probabilities are as follows: | ||
| + | :$${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 0) ={\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) = p_{\rm B} \hspace{0.05cm}.$$ | ||
| + | *In the BSEC model, the corresponding conditional probabilities are equal to $λ$ <br>⇒ see graph on the information page. | ||
| + | * Therefore, the correct <u>solution proposal is 2</u>: | ||
| + | :$$p_{\rm B} = \lambda = 1 - p_{\rm A} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm A} = 1- \lambda\hspace{0.05cm}.$$ | ||
| + | |||
| − | ''' | + | '''(5)''' In the BSEC ("Binary Symmetric Error & Erasure Channel") model, for example: |
| + | :$$ {\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 0) =\varepsilon \hspace{0.05cm}.$$ | ||
| + | *In contrast, for our auxiliary model according to the graph below, the result is: | ||
| + | :$${\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 0) =(1- \lambda) \cdot q \hspace{0.05cm}.$$ | ||
| + | *This gives $q = ε/(1 – λ)$ ⇒ <u>Proposed solution 4</u>. | ||
| + | *The graph uses colours and line type (solid/dotted) to illustrate the relationship between the models. | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(6)''' Using the results of subtasks '''(3)''', '''(4)''' and '''(5)''' we obtain in general for the "Binary Symmetric Error & Erasure Channel": | |
| − | '''4 | + | :$$C_{\rm BSEC} = (1- \lambda) \cdot \left [ 1 - H_{\rm bin}(\frac{\varepsilon}{1- \lambda}) \right ]\hspace{0.05cm},$$ |
| − | $${\rm | + | :or the numerical values for $ε = 0.08$ and $λ = 0.2$: |
| − | + | :$$C_{\rm BSEC} = 0.8 \cdot \big [ 1 - H_{\rm bin}(0.1) \big ] = 0.8 \cdot \left [ 1 - 0.469 \right ] \hspace{0.15cm} \underline {=0.425\,{\rm bit}}\hspace{0.05cm}.$$ | |
| − | $$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''(7)''' The "Binary Symmetric Channel" (BSC) is a special case of the BSEC with $λ = 0$: |
| − | $$C_{\rm | + | :$$ C_{\rm BSC} = 1 - H_{\rm bin}(\varepsilon) = 1 - H_{\rm bin}(0.08) = 1 - 0.402 \hspace{0.15cm} \underline {=0.598\,{\rm bit}}\hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | ''' | + | '''(8)''' The "Binary Erasure Channel" (BEC) is a special case of the BSEC with $ε = 0$: |
| − | + | :$$C_{\rm BEC} = (1- \lambda) \cdot \big [ 1 - H_{\rm bin}(0) \big ] = 1- \lambda\hspace{0.05cm}.$$ | |
| − | ''' | + | *With $λ = 0.2$ , this results in $C_{\rm BEC}\hspace{0.15cm} \underline { = 0.8 \ \rm bit}.$ |
| − | $$C_{\rm BEC} = (1- \lambda) \cdot \ | ||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 109: | Line 130: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^3.3 Application to Digital Signal Transmission^]] |
Latest revision as of 12:57, 24 September 2021
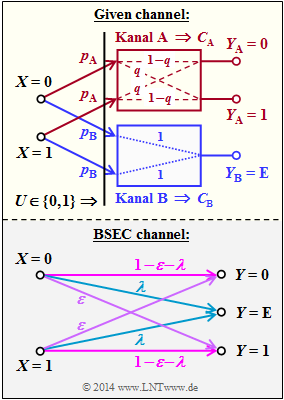
The upper diagram shows two strictly symmetric subchannels $\rm A$ and $\rm B$.
- A strongly symmetric channel is one that is "uniformly dispersive" ⇒ each input symbol $u$ has the same set of transition probabilities:
- $$\left \{ P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.02cm}U}(y\hspace{0.03cm} |\hspace{0.03cm} u) \hspace{-0.05cm}: \hspace{0.25cm}u \in U \right \} \hspace{0.05cm},$$
- moreover, uniformly focusing ⇒ each output symbol $y$ has the same set of transition probabilities:
- $$ \left \{ P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.02cm}U}(y\hspace{0.03cm} |\hspace{0.03cm} u) \hspace{-0.05cm}: \hspace{0.25cm}y \in Y \right \} \hspace{0.05cm}.$$
The random quantity $U = \{0,\ 1\}$ occurs directly at the inputs of the sub-channels $\rm A$ and $\rm B$.
The channel capacity of a strictly symmetrical channel can be calculated much more easily than in the asymmetrical case. However, this will not be discussed in detail in this exercise.
For the capacity of the total channel applies:
- $$ C = p_{\rm A} \cdot C_{\rm A} + p_{\rm B} \cdot C_{\rm B}\hspace{0.05cm}$$
Here $p_{\rm A}$ denotes the probability that the sub-channel $\rm A$ is selected and $C_{\rm A}$ indicates its capacity. The same applies to sub-channel $\rm B$.
Subsequently, the channel capacity of the Binary Symmetric Error & Erasure Channel $\rm (BSEC)$ is also to be determined according to the sketch below (grey background) by deriving the relationship between
- the parameters $p_{\rm A}$, $p_{\rm B}$ and the crossover probability $q$ of the sub-channel model shown above, and
- the parameters $λ$ and $\varepsilon$ of the BSEC model.
Hints:
- The exercise belongs to the chapter Application to Digital Signal Transmission.
- Reference is made in particular to the page Properties of symmetrical channels.
- According to Exercise 3.10Z , the following applies to the channel capacity of the BSC model with the crossover probability $\varepsilon$:
- $$ C_{\rm BSC} = 1 - H_{\rm bin}(\varepsilon)\hspace{0.05cm}.$$
Questions
Solution
(2) Subchannel $\rm B$ is an "erasure channel". Both the sink entropy and irrelevance of this subchannel are zero ⇒ Proposed solution 3.
(3) The capacity $C$ of the total channel can be calculated using the given equation:
- $$ C = p_{\rm A} \cdot C_{\rm A} + p_{\rm B} \cdot C_{\rm B} = p_{\rm A} \cdot \big[1 - H_{\rm bin}(q)\big]\hspace{0.05cm}.$$
Thus, the proposed solution 2 is correct here.
(4) In the model considered so far, the transition probabilities are as follows:
- $${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 0) ={\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) = p_{\rm B} \hspace{0.05cm}.$$
- In the BSEC model, the corresponding conditional probabilities are equal to $λ$
⇒ see graph on the information page. - Therefore, the correct solution proposal is 2:
- $$p_{\rm B} = \lambda = 1 - p_{\rm A} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm A} = 1- \lambda\hspace{0.05cm}.$$
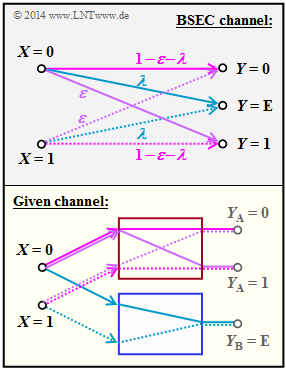
(5) In the BSEC ("Binary Symmetric Error & Erasure Channel") model, for example:
- $$ {\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 0) =\varepsilon \hspace{0.05cm}.$$
- In contrast, for our auxiliary model according to the graph below, the result is:
- $${\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 0) =(1- \lambda) \cdot q \hspace{0.05cm}.$$
- This gives $q = ε/(1 – λ)$ ⇒ Proposed solution 4.
- The graph uses colours and line type (solid/dotted) to illustrate the relationship between the models.
(6) Using the results of subtasks (3), (4) and (5) we obtain in general for the "Binary Symmetric Error & Erasure Channel":
- $$C_{\rm BSEC} = (1- \lambda) \cdot \left [ 1 - H_{\rm bin}(\frac{\varepsilon}{1- \lambda}) \right ]\hspace{0.05cm},$$
- or the numerical values for $ε = 0.08$ and $λ = 0.2$:
- $$C_{\rm BSEC} = 0.8 \cdot \big [ 1 - H_{\rm bin}(0.1) \big ] = 0.8 \cdot \left [ 1 - 0.469 \right ] \hspace{0.15cm} \underline {=0.425\,{\rm bit}}\hspace{0.05cm}.$$
(7) The "Binary Symmetric Channel" (BSC) is a special case of the BSEC with $λ = 0$:
- $$ C_{\rm BSC} = 1 - H_{\rm bin}(\varepsilon) = 1 - H_{\rm bin}(0.08) = 1 - 0.402 \hspace{0.15cm} \underline {=0.598\,{\rm bit}}\hspace{0.05cm}.$$
(8) The "Binary Erasure Channel" (BEC) is a special case of the BSEC with $ε = 0$:
- $$C_{\rm BEC} = (1- \lambda) \cdot \big [ 1 - H_{\rm bin}(0) \big ] = 1- \lambda\hspace{0.05cm}.$$
- With $λ = 0.2$ , this results in $C_{\rm BEC}\hspace{0.15cm} \underline { = 0.8 \ \rm bit}.$