Difference between revisions of "Channel Coding/Bounds for Block Error Probability"
| Line 15: | Line 15: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ We denote the '''number''' of codewords $\underline{x}\hspace{0.05cm}'' \in \mathcal{C}$ with Hamming | + | $\text{Definition:}$ We denote the '''number''' of codewords $\underline{x}\hspace{0.05cm}'' \in \mathcal{C}$ with Hamming distance $i$ from the considered codeword $\underline{x}$ of the same code $\mathcal{C}$ with $W_i(\underline{x})$, where holds: |
::<math>W_i(\underline{x}) = \big \vert \hspace{0.05cm} \left \{ | ::<math>W_i(\underline{x}) = \big \vert \hspace{0.05cm} \left \{ | ||
| Line 88: | Line 88: | ||
::<math>W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = \frac{(1+X)^6}{2^1} \cdot W \left [1 \hspace{-0.05cm}+\hspace{-0.05cm} \left ( \frac {1\hspace{-0.05cm}-\hspace{-0.05cm}X}{1\hspace{-0.05cm}+\hspace{-0.05cm}X}\right )^6 \right ] = 1/2 \cdot \big [( 1\hspace{-0.05cm}+\hspace{-0.05cm}X) ^6 \hspace{-0.05cm}+\hspace{-0.05cm} ( 1-X) ^6 \big ] = 1 \hspace{-0.05cm}+\hspace{-0.05cm} 15 \cdot X^{2} \hspace{-0.05cm}+\hspace{-0.05cm} 15 \cdot X^{4} \hspace{-0.05cm}+\hspace{-0.05cm} X^{6}\hspace{0.05cm}.</math>}}<br> | ::<math>W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = \frac{(1+X)^6}{2^1} \cdot W \left [1 \hspace{-0.05cm}+\hspace{-0.05cm} \left ( \frac {1\hspace{-0.05cm}-\hspace{-0.05cm}X}{1\hspace{-0.05cm}+\hspace{-0.05cm}X}\right )^6 \right ] = 1/2 \cdot \big [( 1\hspace{-0.05cm}+\hspace{-0.05cm}X) ^6 \hspace{-0.05cm}+\hspace{-0.05cm} ( 1-X) ^6 \big ] = 1 \hspace{-0.05cm}+\hspace{-0.05cm} 15 \cdot X^{2} \hspace{-0.05cm}+\hspace{-0.05cm} 15 \cdot X^{4} \hspace{-0.05cm}+\hspace{-0.05cm} X^{6}\hspace{0.05cm}.</math>}}<br> | ||
| − | == Union Bound | + | == Union Bound of the block error probability == |
<br> | <br> | ||
| − | + | We consider as in $\text{Example 1}$ to the distance spectrum the $(5, \hspace{0.02cm} 2)$–block code $\mathcal{C} = \{\underline{x}_0, \underline{x}_1, \underline{x}_2, \underline{x}_3 \}$ and assume that the codeword $\underline{x}_0$ has been sent. The graphic illustrates the situation. | |
| − | [[File:EN_KC_T_1_6_S2b.png|center|frame| | + | [[File:EN_KC_T_1_6_S2b.png|center|frame|Derivation of the Union Bound |class=fit]] |
| − | + | In the error-free case, the code word estimator would then return $\underline{z} = \underline{x}_0$ . Otherwise, a block error would occur (that is, $\underline{z} \ne \underline{x}_0$ and accordingly $\underline{v} \ne \underline{u}_0)$ with probability | |
| − | ::<math>{\rm Pr( | + | ::<math>{\rm Pr(block\:error)} = {\rm Pr}\left (\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.05cm}\cup\hspace{0.05cm}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] \hspace{0.05cm}\cup\hspace{0.05cm}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] \right ) |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | The event "corruption of $\underline{x}_0$ to $\underline{x}_1$" occurs for a given received word $\underline{y}$ according to the [[Channel_Coding/Channel_Models_and_Decision_Structures#Definitions_of_the_different_optimal_receivers|Maximum Likelihood Decision Rule]] "block-wise ML" exactly when holds for the conditional probability density function: | |
::<math>\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} | ::<math>\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} | ||
| Line 105: | Line 105: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | Since $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] $are not necessarily <i>disjoint events</i> (which would thus be mutually exclusive), the [[Theory_of_Stochastic_Signals/Set_Theory_Basics#Union_set| probability of the union set]] is less than or equal to the sum of the individual probabilities: | |
| − | :<math>{\rm Pr( | + | :<math>{\rm Pr(block\:error)} \le {\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.05cm}+\hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] \hspace{0.05cm}+ \hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] \hspace{0.05cm}.</math> |
| − | + | One calls this upper bound for the (block) error probability the '''Union Bound'''. This was already used in the chapter [[Digital_Signal_Transmission/Approximation_of_the_Error_Probability#Union_Bound_-_Upper_bound_for_the_error_probability|approximation of the error probability]] of the book "Digital Signal Transmission".<br> | |
| − | + | We generalize and formalize these results under the assumption that both $\underline{x}$ and $\underline{x}\hspace{0.05cm}'$ belong to the code $\mathcal{C}$ . | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Dann gelten folgende Berechnungsvorschriften:}$ | $\text{Dann gelten folgende Berechnungsvorschriften:}$ | ||
| − | *$\rm | + | *$\rm Block\:error\:probability$: |
| − | ::$${\rm Pr( | + | ::$${\rm Pr(block\:error)} = {\rm Pr} \left ( \bigcup_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm}\big [\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \right )\hspace{0.05cm},$$ |
| − | * | + | *Upper bound after the $\text{Union Bound}$: |
::$${\rm Pr(Union \hspace{0.15cm}Bound)} \le \sum_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm} {\rm Pr}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \hspace{0.05cm},$$ | ::$${\rm Pr(Union \hspace{0.15cm}Bound)} \le \sum_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm} {\rm Pr}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \hspace{0.05cm},$$ | ||
| − | * $\text{ | + | * $\text{Pairwise error probability}$ (according to the MAP or ML criterion.): |
::$${\rm Pr}\hspace{0.02cm}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] = {\rm Pr} \big [ | ::$${\rm Pr}\hspace{0.02cm}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] = {\rm Pr} \big [ | ||
| Line 130: | Line 130: | ||
| − | + | On the next pages, these results are applied to different channels.<br> | |
== Union Bound für das BSC–Modell == | == Union Bound für das BSC–Modell == | ||
| Line 250: | Line 250: | ||
*Bei Kenntnis des vorliegenden Übertragungskanals (BEC, BSC, AWGN oder Abwandlungen hiervon) und dessen Parameter spricht somit vom Aufwand her nichts dagegen, gleich die (genauere) "Union Bound" als obere Schranke für die Blockfehlerwahrscheinlichkeit zu verwenden.}}<br> | *Bei Kenntnis des vorliegenden Übertragungskanals (BEC, BSC, AWGN oder Abwandlungen hiervon) und dessen Parameter spricht somit vom Aufwand her nichts dagegen, gleich die (genauere) "Union Bound" als obere Schranke für die Blockfehlerwahrscheinlichkeit zu verwenden.}}<br> | ||
| − | == Schranken für den (7, 4, 3) | + | == Schranken für den (7, 4, 3)–Hamming Code beim AWGN–Kanal == |
<br> | <br> | ||
Abschließend betrachten wir die Blockfehlerwahrscheinlichkeit und deren Schranken ("Union Bound" und "Bhattacharyya–Schranke" ) für die folgende Konfiguration: | Abschließend betrachten wir die Blockfehlerwahrscheinlichkeit und deren Schranken ("Union Bound" und "Bhattacharyya–Schranke" ) für die folgende Konfiguration: | ||
Revision as of 17:27, 21 July 2022
Contents
Distance spectrum of a linear code
We further assume a linear and binary $(n, \hspace{0.05cm} k)$–block code $\mathcal{C}$ . A major goal of code design is to keep the "block error probability" ${\rm Pr}(\underline{u} \ne \underline{v}) = {\rm Pr}(\underline{z} \ne \underline{x})$ as low as possible. This is achieved by, among other things.
- the minimum distance $d_{\rm min}$ between two codewords $\underline{x}$ and $\underline{x}\hspace{0.05cm}'$ is as large as possible, so that one can correct up to $t = ⌊(d_{\rm min}-1)/2⌋$ bit errors;
- at the same time the minimum distance $d_{\rm min}$ ⇒ worst case occurs as rarely as possible, given all the allowed codewords.
$\text{Definition:}$ We denote the number of codewords $\underline{x}\hspace{0.05cm}'' \in \mathcal{C}$ with Hamming distance $i$ from the considered codeword $\underline{x}$ of the same code $\mathcal{C}$ with $W_i(\underline{x})$, where holds:
- \[W_i(\underline{x}) = \big \vert \hspace{0.05cm} \left \{ \underline{x} \hspace{0.05cm}, \underline{x}{\hspace{0.05cm}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm}\vert\hspace{0.1cm} d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}\hspace{0.05cm}' ) = i \right \} \hspace{0.05cm} \big \vert\hspace{0.05cm}.\]
- The straight lines of the absolute value here denote the number of codewords $\underline{x}\hspace{0.05cm}'$, that satisfy the condition $d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}\hspace{0.05cm}' ) = i $ .
This value is also called multiplicity.
$\text{Example 1:}$ We consider the $(5, \, 2)$ block code $\mathcal{C}$ with the generator matrix
\[{ \boldsymbol{\rm G} } = \begin{pmatrix} 1 &0 &1 &1 &0 \\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.\]
The table shows the hamming distances
- between all codewords $\underline{x}_i$.
- to the reference words $\underline{x}_0$, ... , $\underline{x}_3$.
One recognizes: Independently of the reference word $\underline{x}_i$ holds:
- \[W_0 = 1 \hspace{0.05cm}, \hspace{0.5cm}W_1 = W_2 = 0 \hspace{0.05cm},\hspace{0.5cm} W_3 = 2 \hspace{0.05cm},\hspace{0.5cm} W_4 = 1\]
- \[ \Rightarrow\hspace{0.3cm} d_{\rm min} = 3\hspace{0.05cm}.\]
Not only in this example, but in any linear code, the same multiplicities $W_i$ result for each codeword. Furthermore, since the all-zero word $\underline{0} = (0, 0,\text{ ...} \hspace{0.05cm}, 0)$ is part of every linear binary code, the above definition can also be formulated as follows:
$\text{Definition:}$ The distance spectrum of a linear binary $(n, \hspace{0.03cm} k)$ block code is the set $\{W_i \}$ with $i = 0, 1,$ ... , $n$. Here $W_i$ gives the number of codewords $\underline{x} \in \mathcal{C}$ with Hamming weight $w_{\rm H}(\underline{x}) = i$ .
Often one describes the set $\hspace{0.05cm}\{W_i \}\hspace{0.05cm}$ also as a polynomial with a pseudovariable $X$:
- \[\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} W(X) = \sum_{i=0 }^{n} W_i \cdot Xi^{i} = W_0 + W_1 \cdot X + W_2 \cdot X^{2} + ... \hspace{0.05cm} + W_n \cdot X^{n}\hspace{0.05cm}.\]
It is also called $W(X)$ weight enumerator function.
For example, the weight enumerator function of the $(5, \hspace{0.02cm} 2)$ code $\mathcal{C} = \left \{ \hspace{0.05cm}(0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \hspace{0.05cm} \right \}$ of $\text{Example 1}$:
- \[W(X) = 1 + 2 \cdot X^{3} + X^{4}\hspace{0.05cm}.\]
As can be seen from the "table of its code words" , for the $(7, \hspace{0.02cm}4, \hspace{0.02cm}3)$ Hamming code:
- \[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.\]
The transformation of the distance spectrum $\hspace{0.01cm}\{W_i \}\hspace{0.01cm}$ into the weight enumerator function $W(X)$ also offers great numerical advantages in some exercises. For example, if the Weight Enumerator Function $W(X)$ of a $(n, \hspace{0.03cm} k)$–Block Codes $\mathcal{C}$ is known, then for the corresponding "dual" $(n, \hspace{0.03cm} n-k)$ code $\mathcal{C}_{\rm dual}$:
- \[W_{\rm Dual}(X) = \frac{(1+X)^n}{2^k} \cdot W \left ( \frac{1-X}{1+X} \right )\hspace{0.05cm}.\]
$\text{Example 2:}$ The weight enumerator function $W(X)$ of "single parity–check codes" with $n = 6$, $k = 5$ ⇒ $\text{SPC (6, 5)}$.
This is obtained by comparing all $2^5 = 32$ code words with the all-zero word:
- \[W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = 1 + 15 \cdot X^{2} + 15 \cdot X^{4} + X^{6}\hspace{0.05cm}.\]
Considering the above equation, you get the same result much faster:
- The to $\text{SPC (6, 5)}$ dual code is the "repetition code" $\text{RC (6, 1)}$ with only two codewords $(0, 0, 0, 0, 0, 0)$ and $(1, 1, 1, 1, 1, 1)$:
- \[W_{\rm RC\hspace{0.03cm}(6,\hspace{0.08cm}1)}(X) = 1 + X^{6}\hspace{0.05cm}.\]
- From this it follows for the weight enumerator function of the $\text{SPC (6, 5)}$ according to the above equation with $k = 1$:
- \[W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = \frac{(1+X)^6}{2^1} \cdot W \left [1 \hspace{-0.05cm}+\hspace{-0.05cm} \left ( \frac {1\hspace{-0.05cm}-\hspace{-0.05cm}X}{1\hspace{-0.05cm}+\hspace{-0.05cm}X}\right )^6 \right ] = 1/2 \cdot \big [( 1\hspace{-0.05cm}+\hspace{-0.05cm}X) ^6 \hspace{-0.05cm}+\hspace{-0.05cm} ( 1-X) ^6 \big ] = 1 \hspace{-0.05cm}+\hspace{-0.05cm} 15 \cdot X^{2} \hspace{-0.05cm}+\hspace{-0.05cm} 15 \cdot X^{4} \hspace{-0.05cm}+\hspace{-0.05cm} X^{6}\hspace{0.05cm}.\]
Union Bound of the block error probability
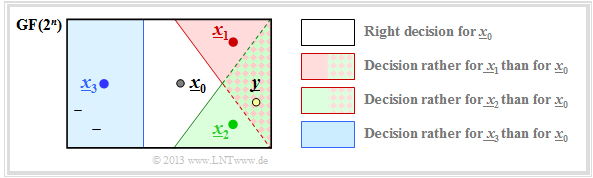
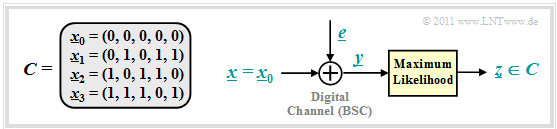
We consider as in $\text{Example 1}$ to the distance spectrum the $(5, \hspace{0.02cm} 2)$–block code $\mathcal{C} = \{\underline{x}_0, \underline{x}_1, \underline{x}_2, \underline{x}_3 \}$ and assume that the codeword $\underline{x}_0$ has been sent. The graphic illustrates the situation.
In the error-free case, the code word estimator would then return $\underline{z} = \underline{x}_0$ . Otherwise, a block error would occur (that is, $\underline{z} \ne \underline{x}_0$ and accordingly $\underline{v} \ne \underline{u}_0)$ with probability
- \[{\rm Pr(block\:error)} = {\rm Pr}\left (\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.05cm}\cup\hspace{0.05cm}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] \hspace{0.05cm}\cup\hspace{0.05cm}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] \right ) \hspace{0.05cm}.\]
The event "corruption of $\underline{x}_0$ to $\underline{x}_1$" occurs for a given received word $\underline{y}$ according to the Maximum Likelihood Decision Rule "block-wise ML" exactly when holds for the conditional probability density function:
- \[\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} f(\underline{x}_{\hspace{0.02cm}0}\hspace{0.02cm} | \hspace{0.05cm}\underline{y}) < f(\underline{x}_{\hspace{0.02cm}1}\hspace{0.02cm} | \hspace{0.05cm}\underline{y}) \hspace{0.05cm}.\]
Since $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] $are not necessarily disjoint events (which would thus be mutually exclusive), the probability of the union set is less than or equal to the sum of the individual probabilities:
\[{\rm Pr(block\:error)} \le {\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.05cm}+\hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] \hspace{0.05cm}+ \hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] \hspace{0.05cm}.\]
One calls this upper bound for the (block) error probability the Union Bound. This was already used in the chapter approximation of the error probability of the book "Digital Signal Transmission".
We generalize and formalize these results under the assumption that both $\underline{x}$ and $\underline{x}\hspace{0.05cm}'$ belong to the code $\mathcal{C}$ .
$\text{Dann gelten folgende Berechnungsvorschriften:}$
- $\rm Block\:error\:probability$:
- $${\rm Pr(block\:error)} = {\rm Pr} \left ( \bigcup_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm}\big [\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \right )\hspace{0.05cm},$$
- Upper bound after the $\text{Union Bound}$:
- $${\rm Pr(Union \hspace{0.15cm}Bound)} \le \sum_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm} {\rm Pr}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \hspace{0.05cm},$$
- $\text{Pairwise error probability}$ (according to the MAP or ML criterion.):
- $${\rm Pr}\hspace{0.02cm}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] = {\rm Pr} \big [ f(\underline{x}\hspace{0.05cm}\vert \hspace{0.05cm}\underline{y}) \le f(\underline{x}\hspace{0.05cm}'\hspace{0.05cm} \vert \hspace{0.05cm}\underline{y}) \big ] \hspace{0.05cm}.$$
On the next pages, these results are applied to different channels.
Union Bound für das BSC–Modell
Wir betrachten weiterhin den beispielhaften $(5, \hspace{0.02cm} 2)$–Code: $\mathcal{C} = \left \{ \hspace{0.05cm}(0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \hspace{0.05cm} \right \}$ und für den digitalen Kanal verwenden wir das BSC–Modell (Binary Symmetric Channel ):
- \[{\rm Pr}(y = 1 \hspace{0.05cm} | \hspace{0.05cm}x = 0 ) = {\rm Pr}(y = 0 \hspace{0.05cm} | \hspace{0.05cm}x = 1 ) = {\rm Pr}(e = 1) = \varepsilon \hspace{0.05cm},\]
- \[{\rm Pr}(y = 0 \hspace{0.05cm} | \hspace{0.05cm}x = 0 ) = {\rm Pr}(y = 1 \hspace{0.05cm} | \hspace{0.05cm}x = 1 ) = {\rm Pr}(e = 0) = 1 -\varepsilon \hspace{0.05cm}.\]
Dann gilt (siehe nachfolgende Grafik):
- Die Codeworte $\underline{x}_0 = (0, 0, 0, 0, 0)$ und $\underline{x}_1 = (0, 1, 0, 1, 1)$ unterscheiden sich in $d = 3$ Bit, wobei $d$ die Hamming–Distanz zwischen $\underline{x}_0$ und $\underline{x}_1$ angibt.
- Ein falsches Decodierergebnis $\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] $ erhält man immer dann, wenn mindestens zwei der drei Bit an den Bitpositionen 2, 4 und 5 verfälscht werden.
- Die Bitpositionen 1 und 3 spielen hier dagegen keine Rolle, da diese für $\underline{x}_0$ und $\underline{x}_1$ gleich sind.
Da der betrachtete Code $t = ⌊(d-1)/2⌋ = 1$ Fehler korrigieren kann, gilt:
- \[{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i=t+1 }^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} = {3 \choose 2} \cdot \varepsilon^{2} \cdot (1 - \varepsilon) + {3 \choose 3} \cdot \varepsilon^{3} =3 \cdot \varepsilon^2 \cdot (1 - \varepsilon) + \varepsilon^3 = {\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big]\hspace{0.05cm}.\]
Hierbei ist berücksichtigt, dass sich $\underline{x}_0 = (0, 0, 0, 0, 0)$ und $\underline{x}_2 = (1, 0, 1, 1, 0)$ ebenfalls in drei Bitpositionen unterscheiden.
Die Codeworte $\underline{x}_0 = (0, 0, 0, 0, 0)$ und $\underline{x}_3 = (1, 1, 1, 0, 1)$ unterscheiden sich dagegen in vier Bitpositionen:
- Zu einer falschen Decodierung des Blocks kommt es deshalb mit Sicherheit, wenn vier oder drei Bit verfälscht werden.
- Eine Verfälschung von zwei Bit hat mit $50$–prozentiger Wahrscheinlichkeit ebenfalls einen Blockfehler zur Folge, wenn man hierfür eine Zufallsentscheidung voraussetzt.
- \[{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big] = \varepsilon^4 + 4 \cdot \varepsilon^3 \cdot (1 - \varepsilon) + {1}/{2} \cdot 6 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^2 \hspace{0.05cm}.\]
Daraus ergibt sich für die "Union Bound":
- \[{\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}\big] +{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}\big] \ge {\rm Pr(Blockfehler)} .\]
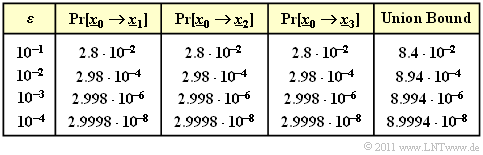
$\text{Beispiel 3:}$ In der Tabelle sind die Ergebnisse für verschiedene Werte des BSC–Parameters $\varepsilon$ zusammengefasst.
Zu erwähnen ist, dass die völlig unterschiedlich zu berechnenden Wahrscheinlichkeiten ${\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}\big]$ und ${\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}3}\big]$ genau das gleiche numerische Ergebnis liefern.
Die obere Schranke nach Bhattacharyya
Eine weitere obere Schranke für die Blockfehlerwahrscheinlichkeit wurde von Bhattacharyya angegeben:
- \[{\rm Pr(Blockfehler)} \le W(X = \beta) -1 = {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]
Hierzu ist anzumerken:
- $W(X)$ ist die oben definierte Gewichtsfunktion, die den verwendeten Kanalcode charakterisiert.
- Der Bhattacharyya–Parameter $\beta$ kennzeichnet den digitalen Kanal. Beispielsweise gilt:
- \[\beta = \left\{ \begin{array}{c} \lambda \\ \sqrt{4 \cdot \varepsilon \cdot (1- \varepsilon)}\\ {\rm e}^{- R \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm B}/N_0} \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r\hspace{0.15cm} das \hspace{0.15cm}BEC-Modell},\\ {\rm f\ddot{u}r\hspace{0.15cm} das \hspace{0.15cm}BSC-Modell}, \\ {\rm f\ddot{u}r\hspace{0.15cm} das \hspace{0.15cm}AWGN-Modell}. \end{array}\]
- Die Bhattacharyya–Schranke liegt stets (und meist deutlich) oberhalb der Kurve für die "Union Bound". Mit dem Ziel, eine für alle Kanäle einheitliche Schranke zu finden, müssen hier sehr viel gröbere Abschätzungen vorgenommen werden als für die "Union Bound".
Wir beschränken uns hier auf die Bhattacharyya–Schranke für das BSC–Modell. Für dessen paarweise Verfälschungswahrscheinlichkeit wurde vorne hergeleitet:
- \[{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] = \sum_{i= \left\lfloor (d-1)/2 \right\rfloor}^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} = \sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i}\hspace{0.05cm}.\]
- Hierbei kennzeichnet $\varepsilon = {\rm Pr}(y = 1\hspace{0.04cm}|\hspace{0.04cm} x = 0) = {\rm Pr}(y = 0\hspace{0.04cm}|\hspace{0.04cm} x = 1)< 0.5$ das Kanalmodell.
- $d = d_{\rm H}(\underline{x}_0,\, \underline{x}_1)$ gibt die Hamming–Distanz der betrachteten Codeworte an.
Um zur Bhattacharyya–Schranke zu kommen, müssen folgende Abschätzungen getroffen werden:
- Für alle $i < d$ gilt $\varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} \le (1 - \varepsilon)^{d/2}$:
- \[{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] \le \big[\varepsilon \cdot (1 - \varepsilon)\big]^{d/2} \cdot \sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \hspace{0.05cm}.\]
- Änderung bezüglich der unteren Grenze der Laufvariablen $i$:
- \[\sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \hspace{0.15cm} < \hspace{0.15cm} \sum_{i= 0 }^{d} {d \choose i} = 2^d\hspace{0.05cm}, \hspace{0.2cm}\beta = 2 \cdot \sqrt{\varepsilon \cdot (1 - \varepsilon)} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] = \beta^{d} \hspace{0.05cm}.\]
- Umsortierung gemäß den Hamming–Gewichten $W_i$ (Hamming–Distanz $d = i$ kommt $W_i$ mal vor):
- \[{\rm Pr(Blockfehler)} \hspace{0.1cm} \le \hspace{0.1cm} \sum_{i= 1 }^{n} W_i \cdot \beta^{i} = 1 + W_1 \cdot \beta + W_2 \cdot \beta^2 + \hspace{0.05cm}\text{ ...} \hspace{0.05cm}+ W_n \cdot \beta^n \hspace{0.05cm}.\]
- Mit der Gewichtsfunktion $W(X)= 1 + W_1 \cdot X + W_2 \cdot X^2 + \text{...} + W_n \cdot X^n$:
- \[{\rm Pr(Blockfehler)} \le W(X = \beta) -1= {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]
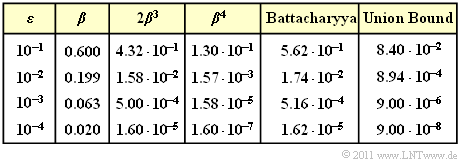
$\text{Beispiel 4:}$ In der Tabelle sind die Bhattacharyya–Ergebnisse für verschiedene Werte des BSC–Parameters $\varepsilon$ zusammengefasst, gültig für den beispielhaften $\text{(5, 2)}$–Code.
Für diesen gilt:
- $$W_0 = 1, \ \ W_1 = W_2 = 0, \ \ W_3 = 2, \ \ W_4 = 1$$
- $$\Rightarrow\hspace{0.3cm} W(X) = 1 + 2 \cdot X^3 + X^4.$$
Damit kann die Bhattacharyya–Schranke berechnet werden:
- \[ {\rm Pr(Bhattacharyya)} = W(\beta) -1 = 2 \cdot \beta^3 + \beta^4\hspace{0.05cm}.\]
Diese stellt eine (oft grobe) Schranke für die Blockfehlerwahrscheinlichkeit dar:
- \[ {\rm Pr(Blockfehler)} \le {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]
$\text{Fazit:}$ Basierend auf dem $\text{Beispiel 3}$ und dem $\text{Beispiel 4}$ (auf dieser Seite) für den einfachen $\text{(5, 2)}$–Blockcode, der allerdings wenig praxisrelevant ist, sowie im Vorgriff auf das $\text{Beispiel 5}$ (auf der nächsten Seite) für den $\text{(7, 4, 3)}$–Hamming–Code fassen wir zusammen:
- Die Blockfehlerwahrscheinlichkeit eines Codiersystems ist oft analytisch nicht angebbar und muss per Simulation ermittelt werden. Gleiches gilt für die Bitfehlerwahrscheinlichkeit.
- Die Union Bound liefert eine obere Schranke für die Blockfehlerwahrscheinlichkeit. Bei vielen Anwendungen (insbesondere bei kurzen Codes) liegt die Union Bound nur geringfügig über der tatsächlichen Fehlerwahrscheinlichkeit.
- Die Bhattacharyya–Schranke liegt beim BEC–Kanal etwa um den Faktor $2$ oberhalb der Union Bound – siehe Aufgabe 1.14. Beim BSC– und beim AWGN–Kanal ist der Abstand deutlich größer. Der Faktor $10$ (und mehr) ist keine Seltenheit.
- Die Bhattacharyya–Schranke $W(\beta) - 1$ wirkt auf den ersten Blick sehr einfach. Trotzdem benötigt man auch hier Kenntnis über die genaue Gewichtsfunktion $W(\xi)$ des Codes.
- Bei Kenntnis des vorliegenden Übertragungskanals (BEC, BSC, AWGN oder Abwandlungen hiervon) und dessen Parameter spricht somit vom Aufwand her nichts dagegen, gleich die (genauere) "Union Bound" als obere Schranke für die Blockfehlerwahrscheinlichkeit zu verwenden.
Schranken für den (7, 4, 3)–Hamming Code beim AWGN–Kanal
Abschließend betrachten wir die Blockfehlerwahrscheinlichkeit und deren Schranken ("Union Bound" und "Bhattacharyya–Schranke" ) für die folgende Konfiguration:
- AWGN–Kanal, gekennzeichnet durch den Quotienten $E_{\rm B}/N_0$,
- Hamming–Code $\text{HC(7, 4, 3)}$ ⇒ $R = 4/7$, $W(X)-1 = 7 \cdot X^3 + 7 \cdot X^4 + X^7$,
- "Soft–Decision" nach dem Maximum–Likelihood–Kriterium.
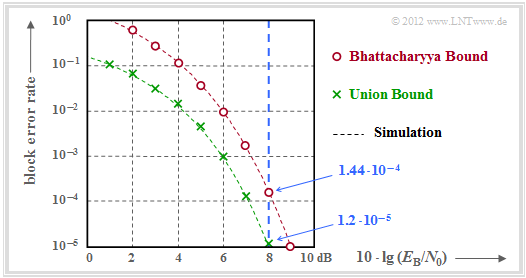
$\text{Beispiel 5:}$ Die Ergebnisse sind in der Grafik zusammengefasst.
- Im Gegensatz zur Grafik im Abschnitt Codiergewinn – Bitfehlerrate bei AWGN ist hier die Blockfehlerrate angegeben und nicht die Bitfehlerrate.
- Näherungsweise ist Letztere um den Faktor $d_{\rm min}/k$ kleiner, falls wie hier $d_{\rm min}< k$ ist. Im vorliegenden Beispiel gilt $d_{\rm min}/k = 0.75$.
- Berechnet wurden nur die Punkte für ganzzahlige $\rm dB$–Werte. Die gestrichelten Linien wurden interpoliert.
- Die rechts angegebenen (blauen) Zahlenwerte gelten für $10 \cdot \lg \, E_{\rm B}/N_0 = 8 \, \rm dB$ ⇒ $E_{\rm B}/N_0 \approx 6.31$ (blaue Vertikale).
Die grünen Kreuze markieren die "Union Bound". Nach dieser gilt:
- \[{\rm Pr(Blockfehler)} \le \sum_{i= d_{\rm min} }^{n} W_i \cdot {\rm Q} \left ( \sqrt{i \cdot {2R \cdot E_{\rm B} }/{N_0} } \right ) \]
- \[\Rightarrow \hspace{0.3cm}{\rm Pr(Blockfehler)} \approx 7 \cdot {\rm Q} (4.65) + 7 \cdot {\rm Q} (5.37) + {\rm Q} (7.10) = \]
- \[\hspace{4.0cm} \approx 7 \cdot 1.66 \cdot 10^{-6} + 7 \cdot 3.93 \cdot 10^{-8}+ 10^{-9} = 1.2 \cdot 10^{-5} \hspace{0.05cm}.\]
- Die Zahlenwerte machen deutlich, dass die Union Bound im wesentlichen durch den ersten Term bestimmt wird:
- \[{\rm Pr(Union\hspace{0.15cm} Bound)} \approx W_{d_{\rm min} } \cdot {\rm Q} \left ( \sqrt{d_{\rm min} \cdot {2R \cdot E_{\rm B} }/{N_0} } \right ) = 1.16 \cdot 10^{-5} \hspace{0.05cm}.\]
- Allerdings ist diese so genannte "Truncated Union Bound" nicht mehr bei allen Anwendungen eine echte Schranke für die Blockfehlerwahrscheinlichkeit, sondern ist als Näherung zu verstehen.
- Die Bhattacharyya–Schranke ist in der Grafik durch rote Punkte markiert. Diese liegt aufgrund der stark vereinfachten Chernoff–Rubin Bound ${\rm Q}(x) \le {\rm e}^{-x^2/2}$ deutlich über der Union Bound.
- Zum Beispiel erhält man für $10 \cdot \lg \, E_{\rm B}/N_0 = 8 \, \rm dB$ mit $\beta = {\rm e}^{-R \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm B}/N_0} \approx 0.027$ gegenüber der Union Bound einen mehr als zehnfachen Wert:
- \[{\rm Pr(Bhattacharyya)} = W(\beta) -1 = 7 \cdot \beta^3 + 7 \cdot \beta^4 + \beta^7 \approx 1.44 \cdot 10^{-4} \hspace{0.05cm}.\]
Aufgaben zum Kapitel
Aufgabe 1.14: Bhattacharyya–Schranke für BEC
Aufgabe 1.15: Distanzspektren von HC (7, 4, 3) und HC (8, 4, 4)
Aufgabe 1.16: Fehlerwahrscheinlichkeitsschranken für AWGN
Aufgabe 1.16Z: Schranken für die Gaußsche Fehlerfunktion