Difference between revisions of "Channel Coding/Definition and Properties of Reed-Solomon Codes"
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü=Reed–Solomon–Codes | + | |Untermenü=Reed–Solomon–Codes and Their Decoding |
| − | |Vorherige Seite= | + | |Vorherige Seite=Extension Field |
| − | |Nächste Seite= | + | |Nächste Seite=Reed-Solomon Decoding for the Erasure Channel |
}} | }} | ||
| − | == | + | == Coding principle and code parameters == |
<br> | <br> | ||
| − | + | A <i>Reed–Solomon Code</i> – hereafter sometimes shortened to '''RS code''' is a [[Channel_Coding/General_Description_of_Linear_Block_Codes#Linear_codes_and_cyclic_codes| "linear block code"]] that is | |
| − | [[File:P ID2515 KC T 2 3 S1 v2.png|right|frame| | + | [[File:P ID2515 KC T 2 3 S1 v2.png|right|frame|Linear $(n, \, k)$ block code|class=fit]] |
| − | * | + | *an information block $\underline{u}$ with $k$ symbols. |
| − | * | + | *assings a corresponding codeword $\underline{c}$ with $n > k$ |
| − | + | symbols. These codes, still widely used today, were invented as early as the early 1960s by [https://en.wikipedia.org/wiki/Irving_S._Reed "Irving Stoy Reed"] and [https://en.wikipedia.org/wiki/Gustave_Solomon "Gustave Solomon"] .<br> | |
| − | + | In the chapter [[Channel_Coding/Objective_of_Channel_Coding#Block_diagram_and_requirements|"Objective of Channel Coding"]] the information block was denoted by $\underline{u}= (u_1,$ ... , $u_k)$ and the codeword by $\underline{x}= (x_1,$ ... , $x_n)$ . | |
| − | + | The nomenclature change $\underline{x} \to \underline{c}$ (see graphic) was made to eliminate confusion with the argument of polynomials and to simplify the description of RS codes. | |
| − | + | All the properties of linear cyclic block codes mentioned in the section [[Channel_Coding/General_Description_of_Linear_Block_Codes#Linear_codes_and_cyclic_codes|"linear codes and cyclic codes"]] also apply to a Reed–Solomon–code. In addition: | |
| + | |||
| + | *Construction and decoding of Reed–Solomon codes are based on the arithmetic of a Galois field ${\rm GF}(q)$, where we restrict ourselves here to binary extension fields with $q=2^m$ elements : | ||
| − | |||
::<math>{\rm GF}(2^m) = \big \{\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} | ::<math>{\rm GF}(2^m) = \big \{\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} | ||
\alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}\text{...}\hspace{0.1cm}, \alpha^{q-2}\hspace{0.05cm} \big \}\hspace{0.05cm}. </math> | \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}\text{...}\hspace{0.1cm}, \alpha^{q-2}\hspace{0.05cm} \big \}\hspace{0.05cm}. </math> | ||
| − | * | + | *Principally different from the first chapter is that the coefficients $u_0$, $u_1$, ... , $u_{k-1}$ now no longer specify individual bits of information $(0$ or $1)$ but are also elements of ${\rm GF}(2^m)$ . Each of the $n$ symbols represents $m$ bits.<br> |
| − | * | + | *For Reed–Solomon codes, the parameter $n$ (code length) is always equal to the number of elements of the Galois field excluding the zero word: $n= q-1$. <br>We use the following nomenclature for this purpose: |
::<math>{\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} | ::<math>{\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} | ||
\alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, \alpha^{n-1}\hspace{0.05cm} \big \}\hspace{0.05cm}. </math> | \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, \alpha^{n-1}\hspace{0.05cm} \big \}\hspace{0.05cm}. </math> | ||
| − | * | + | *The $k$ coefficients $u_i \in {\rm GF}(2^m)$ of the information block $\underline{u}$, where for the index $ 0 \le i < k$ holds, can also be formally expressed by a polynomial $u(x)$ . The degree of the polynomial is here $k-1$: |
::<math>u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}\text{...}\hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) | ::<math>u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}\text{...}\hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *The $n$ symbols of the associated codeword $\underline{c}= (c_0, c_1,$ ... , $c_{n-1})$ result with this polynomial $u(x)$ to be |
::<math>c_0 = u(\alpha^{0}) \hspace{0.05cm},\hspace{0.3cm} c_1 = u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm},\hspace{0.3cm} c_{n-1}= u(\alpha^{n-1}) \hspace{0.05cm}.</math> | ::<math>c_0 = u(\alpha^{0}) \hspace{0.05cm},\hspace{0.3cm} c_1 = u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm},\hspace{0.3cm} c_{n-1}= u(\alpha^{n-1}) \hspace{0.05cm}.</math> | ||
| − | * | + | *Mostly the code symbols $c_i \in {\rm GF}(2^m)$ are converted back to binary ⇒ ${\rm GF}(2)$ before transmission, where each symbol is then represented by $m$ bits.<br> |
| − | + | We briefly summarize these statements: | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ A $(n, k)$'''–Reed–Solomon code''' for the Galois field ${\rm GF}(2^m)$ is defined by. |
| − | * | + | *the $n= 2^{m-1}$ elements of ${\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} =\{ \alpha^0, \alpha^1, \, \text{...} \, , \alpha^{n-1}\}$, where $\alpha$ denotes a [[Channel_Coding/Extension_Field#Binary_extension_fields_.E2.80.93_Primitive_polynomials|"primitive element"]] of ${\rm GF}(2^m)$ denotes, |
| − | * | + | *an information blockt $\underline{u}$ matched [[Channel_Coding/Extension_Field#Generalized_definition_of_an_extension_field|"polynomial"]] of degree $k-1$ the form |
::<math>u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}... \hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) | ::<math>u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}... \hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | Thus, the $(n, k)$–Reed–Solomon code can be described as. | |
::<math>C_{\rm RS} = \Big \{ \underline {c} = \big ( u(\alpha^{0}) \hspace{0.05cm},\hspace{0.1cm} u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, u(\alpha^{n-1})\hspace{0.1cm} \big ) | ::<math>C_{\rm RS} = \Big \{ \underline {c} = \big ( u(\alpha^{0}) \hspace{0.05cm},\hspace{0.1cm} u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, u(\alpha^{n-1})\hspace{0.1cm} \big ) | ||
| Line 64: | Line 65: | ||
\Big \} \hspace{0.05cm}.</math>}}<br> | \Big \} \hspace{0.05cm}.</math>}}<br> | ||
| − | + | The previous information will now be illustrated by two simple examples. | |
| − | [[File:P ID2517 KC T 2 3 S1b v3.png|right|frame|$\rm GF(2^2)$ in | + | [[File:P ID2517 KC T 2 3 S1b v3.png|right|frame|$\rm GF(2^2)$ in three different representations: <br>Exponential, polynomial and coefficient form |class=fit]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
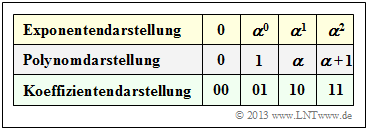
| − | $\text{ | + | $\text{Example 1:}$ We consider the following code parameters: |
::<math>k = 2 \hspace{0.05cm},\hspace{0.15cm}n = 3 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \underline {u} = (u_0, u_1)\hspace{0.05cm},\hspace{0.15cm} | ::<math>k = 2 \hspace{0.05cm},\hspace{0.15cm}n = 3 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \underline {u} = (u_0, u_1)\hspace{0.05cm},\hspace{0.15cm} | ||
| Line 76: | Line 77: | ||
\hspace{0.5cm} \Rightarrow \hspace{0.5cm} m = 2\hspace{0.05cm}.</math> | \hspace{0.5cm} \Rightarrow \hspace{0.5cm} m = 2\hspace{0.05cm}.</math> | ||
| − | + | Starting from the conditional equation $p(\alpha) = \alpha^2 + \alpha + 1 = 0$ ⇒ $\alpha^2 = \alpha + 1$ one obtains the assignments between | |
| − | * | + | *the exponential representation, |
| − | * | + | *the polynomial representation and |
| − | * | + | *the coefficient representation |
| − | + | of ${\rm GF}(2^2)$ according to the above table. From this it can be seen: | |
| − | * | + | *The coefficient vector is expressed by the polynomial $u(x) = u_0 + u_1 \cdot x$ . The polynomial degree is $k- 1 = 1$. |
| − | * | + | *For $u_0 = \alpha^1$ and $u_1 = \alpha^2$ we obtain, for example, the polynomial $u(x) = \alpha + \alpha^2 \cdot x$ and thus |
::<math>c_0 = u (x = \alpha^0) = u (x = 1) = \alpha + \alpha^2 \cdot 1 = \alpha + (\alpha + 1) =1 \hspace{0.05cm},</math> | ::<math>c_0 = u (x = \alpha^0) = u (x = 1) = \alpha + \alpha^2 \cdot 1 = \alpha + (\alpha + 1) =1 \hspace{0.05cm},</math> | ||
| Line 91: | Line 92: | ||
::<math>c_2 =u (x = \alpha^2) = \alpha + \alpha^2 \cdot \alpha^2 = \alpha + \alpha^4 = \alpha + \alpha^1 = 0 \hspace{0.05cm}.</math> | ::<math>c_2 =u (x = \alpha^2) = \alpha + \alpha^2 \cdot \alpha^2 = \alpha + \alpha^4 = \alpha + \alpha^1 = 0 \hspace{0.05cm}.</math> | ||
| − | + | This results in the following assignments on symbol or bit level: | |
::<math>\underline {u} =(\alpha^1, \ \alpha^2)\hspace{0.57cm}\leftrightarrow\hspace{0.3cm} | ::<math>\underline {u} =(\alpha^1, \ \alpha^2)\hspace{0.57cm}\leftrightarrow\hspace{0.3cm} | ||
| Line 99: | Line 100: | ||
[[File:P ID2570 KC T 2 3 S1bb v3.png|right|frame||Codetabelle des $\text{RSC (3, 2, 2)}_4$]] | [[File:P ID2570 KC T 2 3 S1bb v3.png|right|frame||Codetabelle des $\text{RSC (3, 2, 2)}_4$]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
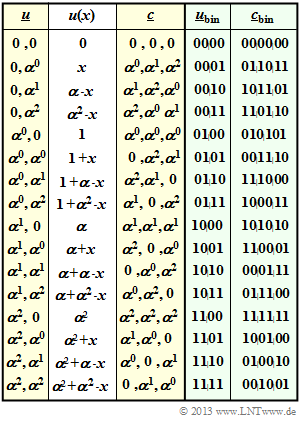
| − | $\text{ | + | $\text{Example 2:}$ |
| − | + | On the right is the code table of the $\text{RSC (3, 2, 2)}_4$ named Reed–Solomon code. | |
| − | * | + | *The label refers to the parameters $n=3$, $k=2$, $d_{\rm min}=2$ and $q = 4$. |
| − | *In | + | *In columns 1 to 3, one can see the relationship $\underline {u} \ → \ u(x) \ → \ \underline {c}$. |
| − | *In | + | *In the last two columns, the coding rule $\underline {u}_{\rm bin} \ ↔ \ \underline {c}_{\rm bin}$ is given.<br> |
| − | + | For clarification again the entry for $(\alpha^0, \ \alpha^2)$: | |
::<math>u(x) = u_0 + u_1 \cdot x = \alpha^0 + \alpha^2 \cdot x. </math> | ::<math>u(x) = u_0 + u_1 \cdot x = \alpha^0 + \alpha^2 \cdot x. </math> | ||
| − | + | This results in the following code symbols: | |
::<math>c_0 = u (x = \alpha^0) = 1 + \alpha^2 \cdot 1 = 1 + (1+\alpha ) =\alpha \hspace{0.05cm},</math> | ::<math>c_0 = u (x = \alpha^0) = 1 + \alpha^2 \cdot 1 = 1 + (1+\alpha ) =\alpha \hspace{0.05cm},</math> | ||
| Line 116: | Line 117: | ||
::<math>c_2 =u (x = \alpha^2) = 1 + \alpha^2 \cdot \alpha^2 = 1 + \alpha = \alpha^2 \hspace{0.05cm}.</math> | ::<math>c_2 =u (x = \alpha^2) = 1 + \alpha^2 \cdot \alpha^2 = 1 + \alpha = \alpha^2 \hspace{0.05cm}.</math> | ||
| − | <i> | + | <i>Hints:</i> |
| − | * | + | *From the element set $\{0, \ \alpha^0 = 1, \ \alpha^1 = \alpha, \ \alpha^2\}$ it should not be concluded that for this code the 3D–representation with axes $\alpha^0 = 1$, $\alpha^1 = \alpha$, $\alpha^2$ applies. See section [[Channel_Coding/Extension_Field#Binary_extension_fields_.E2.80.93_Primitive_polynomials|"primitive polynomials"]] – example 5. |
| − | * | + | *On the contrary, from the coefficient representation in $\text{Example 1}$ it is clear that ${\rm GF} (2^2)$ is two-dimensional, where the axes of the two dimensional representation are to be labeled $\alpha^0 = 1$ and $\alpha^1 = \alpha$ . |
}}<br> | }}<br> | ||
| − | == | + | == Generator matrix of Reed-Solomon codes == |
<br> | <br> | ||
Da es sich beim Reed–Solomon–Code um einen linearen Blockcode handelt, ist der Zusammenhang zwischen Informationswort $\underline {u}$ und Codewort $\underline {c}$ durch die [[Channel_Coding/Allgemeine_Beschreibung_linearer_Blockcodes#Codefestlegung_durch_die_Generatormatrix| Generatormatrix]] $\boldsymbol{\rm G}$ gegeben: | Da es sich beim Reed–Solomon–Code um einen linearen Blockcode handelt, ist der Zusammenhang zwischen Informationswort $\underline {u}$ und Codewort $\underline {c}$ durch die [[Channel_Coding/Allgemeine_Beschreibung_linearer_Blockcodes#Codefestlegung_durch_die_Generatormatrix| Generatormatrix]] $\boldsymbol{\rm G}$ gegeben: | ||
Revision as of 22:14, 1 September 2022
Contents
Coding principle and code parameters
A Reed–Solomon Code – hereafter sometimes shortened to RS code is a "linear block code" that is
- an information block $\underline{u}$ with $k$ symbols.
- assings a corresponding codeword $\underline{c}$ with $n > k$
symbols. These codes, still widely used today, were invented as early as the early 1960s by "Irving Stoy Reed" and "Gustave Solomon" .
In the chapter "Objective of Channel Coding" the information block was denoted by $\underline{u}= (u_1,$ ... , $u_k)$ and the codeword by $\underline{x}= (x_1,$ ... , $x_n)$ .
The nomenclature change $\underline{x} \to \underline{c}$ (see graphic) was made to eliminate confusion with the argument of polynomials and to simplify the description of RS codes.
All the properties of linear cyclic block codes mentioned in the section "linear codes and cyclic codes" also apply to a Reed–Solomon–code. In addition:
- Construction and decoding of Reed–Solomon codes are based on the arithmetic of a Galois field ${\rm GF}(q)$, where we restrict ourselves here to binary extension fields with $q=2^m$ elements :
- \[{\rm GF}(2^m) = \big \{\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}\text{...}\hspace{0.1cm}, \alpha^{q-2}\hspace{0.05cm} \big \}\hspace{0.05cm}. \]
- Principally different from the first chapter is that the coefficients $u_0$, $u_1$, ... , $u_{k-1}$ now no longer specify individual bits of information $(0$ or $1)$ but are also elements of ${\rm GF}(2^m)$ . Each of the $n$ symbols represents $m$ bits.
- For Reed–Solomon codes, the parameter $n$ (code length) is always equal to the number of elements of the Galois field excluding the zero word: $n= q-1$.
We use the following nomenclature for this purpose:
- \[{\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, \alpha^{n-1}\hspace{0.05cm} \big \}\hspace{0.05cm}. \]
- The $k$ coefficients $u_i \in {\rm GF}(2^m)$ of the information block $\underline{u}$, where for the index $ 0 \le i < k$ holds, can also be formally expressed by a polynomial $u(x)$ . The degree of the polynomial is here $k-1$:
- \[u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}\text{...}\hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) \hspace{0.05cm}.\]
- The $n$ symbols of the associated codeword $\underline{c}= (c_0, c_1,$ ... , $c_{n-1})$ result with this polynomial $u(x)$ to be
- \[c_0 = u(\alpha^{0}) \hspace{0.05cm},\hspace{0.3cm} c_1 = u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm},\hspace{0.3cm} c_{n-1}= u(\alpha^{n-1}) \hspace{0.05cm}.\]
- Mostly the code symbols $c_i \in {\rm GF}(2^m)$ are converted back to binary ⇒ ${\rm GF}(2)$ before transmission, where each symbol is then represented by $m$ bits.
We briefly summarize these statements:
$\text{Definition:}$ A $(n, k)$–Reed–Solomon code for the Galois field ${\rm GF}(2^m)$ is defined by.
- the $n= 2^{m-1}$ elements of ${\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} =\{ \alpha^0, \alpha^1, \, \text{...} \, , \alpha^{n-1}\}$, where $\alpha$ denotes a "primitive element" of ${\rm GF}(2^m)$ denotes,
- an information blockt $\underline{u}$ matched "polynomial" of degree $k-1$ the form
- \[u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}... \hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) \hspace{0.05cm}.\]
Thus, the $(n, k)$–Reed–Solomon code can be described as.
- \[C_{\rm RS} = \Big \{ \underline {c} = \big ( u(\alpha^{0}) \hspace{0.05cm},\hspace{0.1cm} u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, u(\alpha^{n-1})\hspace{0.1cm} \big ) \hspace{0.1cm} \big \vert \hspace{0.2cm} u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i}\hspace{0.05cm},\hspace{0.2cm} u_i \in {\rm GF}(2^m) \Big \} \hspace{0.05cm}.\]
The previous information will now be illustrated by two simple examples.
$\text{Example 1:}$ We consider the following code parameters:
- \[k = 2 \hspace{0.05cm},\hspace{0.15cm}n = 3 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \underline {u} = (u_0, u_1)\hspace{0.05cm},\hspace{0.15cm} \underline {c} = (c_0, c_1, c_2)\hspace{0.05cm},\]
- \[q = n+1 = 4 \hspace{0.45cm} \Rightarrow \hspace{0.5cm} {\rm GF} (q) = {\rm GF} (2^m) \hspace{0.5cm} \Rightarrow \hspace{0.5cm} m = 2\hspace{0.05cm}.\]
Starting from the conditional equation $p(\alpha) = \alpha^2 + \alpha + 1 = 0$ ⇒ $\alpha^2 = \alpha + 1$ one obtains the assignments between
- the exponential representation,
- the polynomial representation and
- the coefficient representation
of ${\rm GF}(2^2)$ according to the above table. From this it can be seen:
- The coefficient vector is expressed by the polynomial $u(x) = u_0 + u_1 \cdot x$ . The polynomial degree is $k- 1 = 1$.
- For $u_0 = \alpha^1$ and $u_1 = \alpha^2$ we obtain, for example, the polynomial $u(x) = \alpha + \alpha^2 \cdot x$ and thus
- \[c_0 = u (x = \alpha^0) = u (x = 1) = \alpha + \alpha^2 \cdot 1 = \alpha + (\alpha + 1) =1 \hspace{0.05cm},\]
- \[c_1 =u (x = \alpha^1) = \alpha + \alpha^2 \cdot \alpha = \alpha + \alpha^3 = \alpha + \alpha^0 = \alpha + 1 = \alpha^2 \hspace{0.05cm},\]
- \[c_2 =u (x = \alpha^2) = \alpha + \alpha^2 \cdot \alpha^2 = \alpha + \alpha^4 = \alpha + \alpha^1 = 0 \hspace{0.05cm}.\]
This results in the following assignments on symbol or bit level:
- \[\underline {u} =(\alpha^1, \ \alpha^2)\hspace{0.57cm}\leftrightarrow\hspace{0.3cm} \underline {c} = (1, \ \alpha^2, \ 0)\hspace{0.05cm},\hspace{1cm}\underline {u}_{\rm bin} =(1,\ 0,\ 1,\ 1)\hspace{0.3cm}\leftrightarrow\hspace{0.3cm} \underline {c}_{\rm bin} = (0,\ 1,\ 1,\ 1,\ 0,\ 0)\hspace{0.05cm}.\]
$\text{Example 2:}$ On the right is the code table of the $\text{RSC (3, 2, 2)}_4$ named Reed–Solomon code.
- The label refers to the parameters $n=3$, $k=2$, $d_{\rm min}=2$ and $q = 4$.
- In columns 1 to 3, one can see the relationship $\underline {u} \ → \ u(x) \ → \ \underline {c}$.
- In the last two columns, the coding rule $\underline {u}_{\rm bin} \ ↔ \ \underline {c}_{\rm bin}$ is given.
For clarification again the entry for $(\alpha^0, \ \alpha^2)$:
- \[u(x) = u_0 + u_1 \cdot x = \alpha^0 + \alpha^2 \cdot x. \]
This results in the following code symbols:
- \[c_0 = u (x = \alpha^0) = 1 + \alpha^2 \cdot 1 = 1 + (1+\alpha ) =\alpha \hspace{0.05cm},\]
- \[c_1 = u (x = \alpha^1) = 1 + \alpha^2 \cdot \alpha = 1 + (1+\alpha ) \cdot \alpha = 1 + \alpha + \alpha^2 = 0 \hspace{0.05cm},\]
- \[c_2 =u (x = \alpha^2) = 1 + \alpha^2 \cdot \alpha^2 = 1 + \alpha = \alpha^2 \hspace{0.05cm}.\]
Hints:
- From the element set $\{0, \ \alpha^0 = 1, \ \alpha^1 = \alpha, \ \alpha^2\}$ it should not be concluded that for this code the 3D–representation with axes $\alpha^0 = 1$, $\alpha^1 = \alpha$, $\alpha^2$ applies. See section "primitive polynomials" – example 5.
- On the contrary, from the coefficient representation in $\text{Example 1}$ it is clear that ${\rm GF} (2^2)$ is two-dimensional, where the axes of the two dimensional representation are to be labeled $\alpha^0 = 1$ and $\alpha^1 = \alpha$ .
Generator matrix of Reed-Solomon codes
Da es sich beim Reed–Solomon–Code um einen linearen Blockcode handelt, ist der Zusammenhang zwischen Informationswort $\underline {u}$ und Codewort $\underline {c}$ durch die Generatormatrix $\boldsymbol{\rm G}$ gegeben:
- \[\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.\]
Wie bei jedem linearen $(n, k)$–Blockcode besteht die Generatormatrix aus $k$ Zeilen und $n$ Spalten. Im Gegensatz zum Kapitel Allgemeine Beschreibung linearer Blockcodes sind nun aber die Elemente der Generatormatrix nicht mehr binär $(0$ oder $1)$, sondern entstammen dem Galoisfeld ${\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} $.
$\text{Beispiel 3:}$ Wir betrachten wie im $\text{Beispiel 2}$ (vorherige Seite) den $\text{RSC (3, 2, 2)}_4$, dessen Generatormatrix folgende Form hat:
\[ { \boldsymbol{\rm G} } = \begin{pmatrix} g_{00} & g_{01} & g_{02}\\ g_{10} & g_{11} & g_{12} \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} g_{ij} \in {\rm GF}(2^2) \hspace{-0.01cm}\setminus \hspace{-0.01cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} \hspace{0.05cm},\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm}\big \}\hspace{0.05cm}. \]
Daneben gilt:
- Die erste Zeile von $\boldsymbol{\rm G}$ gibt das Codewort für das Informationswort $\underline {u}_1 = (1, 0)$ an bzw. für die Polynomfunktion $u_1(x) = 1$. Damit erhält man die Matrixelemente der ersten Zeile zu
- \[g_{00} = u_{1}(\alpha^{0}) = 1\hspace{0.05cm},\hspace{0.3cm} g_{01} = u_{1}(\alpha^{1}) = 1\hspace{0.05cm},\hspace{0.3cm} g_{02} = u_{1}(\alpha^{2}) = 1\hspace{0.05cm}.\]
- Die zweite Zeile ist gleich dem Codewort für das Informationswort $\underline {u}_2 = (0, 1)$ ⇒ $u_2(x) = x$. Die Matrixelemente der zweiten Zeile lauten somit:
- \[g_{10} = u_{2}(\alpha^{0}) = \alpha^{0} = 1\hspace{0.05cm},\hspace{0.3cm} g_{11} = u_{2}(\alpha^{1}) = \alpha \hspace{0.05cm},\hspace{0.3cm} g_{12} = u_{2}(\alpha^{2}) = \alpha^{2}\hspace{0.05cm}.\]
- \[\Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G} } = \begin{pmatrix} 1 & 1 & 1\\ 1 & \alpha & \alpha^2 \end{pmatrix}\hspace{0.05cm}.\]
Für das Informationswort $\underline {u}= (u_0, \ u_1)$ mit den Symbolen $u_0, \ u_1 ∈ \{0, \ \alpha^0, \ \alpha^1 = \alpha, \ \alpha^2\}$ erhält man unter Berücksichtigung der beiden Gleichungen $\alpha^2 = \alpha + 1$ sowie $\alpha^3 = \alpha^0 = 1$ wiederum die Codetabelle des $\text{RSC (3, 2, 2)}_4$ auf Symbolebene.
- Man erhält natürlich mit der Generatormatrix genau die gleiche Codetabelle $\underline {u} ↔ \underline {c}$ wie nach der Berechnung über die Funktion $u(x)$.
- Die entsprechende Codetabelle auf Bitebene (siehe $\text{Beispiel 2}$ auf der vorherigen Seite) ergibt sich wieder, wenn man die Elemente nicht in Exponentendarstellung angibt, sondern in Koeffizientenform:
- \[(0, \hspace{0.1cm}\alpha^{0}, \hspace{0.1cm}\alpha^{1}, \hspace{0.1cm}\alpha^{2}) \hspace{0.3cm}\Leftrightarrow\hspace{0.3cm}(00, \hspace{0.1cm}01, \hspace{0.1cm}10, \hspace{0.1cm}11) \hspace{0.05cm}. \]
Generatormatrix und Prüfmatrix
Wir verallgemeinern nun das Ergebnis der letzten Seite für einen Reed–Solomon–Code mit
- der Dimension $k$ (Symbolanzahl pro Informationsblock),
- der Codewortlänge $n$ (Symbolanzahl pro Codewort).
Generatormatrix $\boldsymbol{\rm G}$ $(k$ Zeilen, $n$ Spalten$)$ und Prüfmatrix $\boldsymbol{\rm H}$ $(n-k$ Zeilen, $n$ Spalten$)$ müssen gemeinsam folgende Gleichung erfüllen:
- \[{ \boldsymbol{\rm G}} \cdot { \boldsymbol{\rm H }}^{\rm T}= { \boldsymbol{\rm 0}}\hspace{0.05cm}.\]
Hierbei bezeichnet $\boldsymbol{\rm 0}$ eine Nullmatrix $($alle Elemente gleich $0)$ mit $k$ Zeilen und $n-k$ Spalten.
$\text{Beispiel 4:}$ Wir betrachten den $\text{RSC (7, 3, 5)}_8$ ⇒ Codeparameter $n= 7$, $k= 3$, basierend auf dem Galoisfeld $\rm GF(2^3 = 8)$ mit der Nebenbedingung $\alpha^3 =\alpha + 1$. Beachten Sie hinsichtlich der Codebezeichnung:
- Der dritte Parameter der für Blockcodes üblichen Nomenklatur nennt die freie Distanz $d_{\rm min}= 5$.
- Anders als bei den im Kapitel Beispiele binärer Blockcodes behandelten binären Codes (Single Parity–check Code, Repetition Code, Hamming Code) wird bei den Reed–Solomon–Codes noch der Hinweis $q$ zum Galoisfeld hinzugefügt $($hier: $q = 8)$.
Alle Elemente der Generatormatrix und der Prüfmatrix,
- \[{ \boldsymbol{\rm G} } = \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} \end{pmatrix}\hspace{0.05cm},\hspace{0.4cm} { \boldsymbol{\rm H} } = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4}\\ 1 & \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2} & \alpha^{6} & \alpha^{3} \end{pmatrix}\hspace{0.05cm}, \]
entstammen dem Galoisfeld ${\rm GF}(2^3) \hspace{-0.01cm}\setminus \hspace{-0.01cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} \hspace{0.05cm},\hspace{0.1cm}\alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm},\hspace{0.1cm} \alpha^{3} \hspace{0.05cm},\hspace{0.1cm}\alpha^{4}\hspace{0.05cm},\hspace{0.1cm} \alpha^{5} \hspace{0.05cm},\hspace{0.1cm} \alpha^{6} \hspace{0.05cm}\big \}$. Für das Matrixprodukt gilt:
- \[{ \boldsymbol{\rm G} } \cdot { \boldsymbol{\rm H } }^{\rm T}= \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1\\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5}\\ \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2}\\ \alpha^5 & \alpha^{3} & \alpha^{1} & \alpha^{6}\\ \alpha^6 & \alpha^{5} & \alpha^{4} & \alpha^{3} \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \hspace{0.05cm}.\]
Dies soll hier nur für zwei Elemente nachgewiesen werden:
- Erste Zeile, erste Spalte:
- \[1 \hspace{0.1cm} \cdot \hspace{0.1cm} \big [1 + \alpha^1 + \alpha^2 + \alpha^3 + \alpha^4 + \alpha^5 + \alpha^6 \big ] = 1 + \alpha + \alpha^2 + (\alpha + 1) + (\alpha^2 + \alpha)+ (\alpha^2 + \alpha +1)+ (\alpha^2 + 1) = 0 \hspace{0.05cm}; \]
- Letzte Zeile, letzte Spalte:
- \[1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 + \alpha^2 \cdot \alpha^4 + \alpha^4 \cdot \alpha^1 + \alpha^6 \cdot \alpha^5+ \alpha^1 \cdot \alpha^2+ \alpha^3 \cdot \alpha^6+ \alpha^5 \cdot \alpha^3= 1 + \alpha^6 + \alpha^5 + \alpha^{11} + \alpha^{3}+ \alpha^{9}+ \alpha^{8} =\]
- \[ \hspace{1.5cm} = \hspace{0.15cm} 1 + \alpha^6 + \alpha^5 + \alpha^{4} + \alpha^{3}+ \alpha^{2}+ \alpha^{1} =0 \hspace{0.05cm}.\]
Singleton–Schranke und minimale Distanz
Eine wichtige Kenngröße eines jeden Blockcodes ist die minimale Distanz zwischen zwei beliebigen Codeworten $\underline {c}_i$ und $\underline {c}_j$.
- Die Reed–Solomon–Codes gehören zur Klasse der linearen und zyklischen Codes. Bei diesen kann man vom Nullwort $\underline {c}_0 = (0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm}, 0)$ als Bezugsgröße ausgehen.
- Aus der Anzahl der Nullen in den anderen Codeworten $\underline {c}_j ≠ \underline {c}_0$ lässt sich das Distanzspektrum $\{ \hspace{0.05cm}W_j\hspace{0.05cm}\}$ angeben.
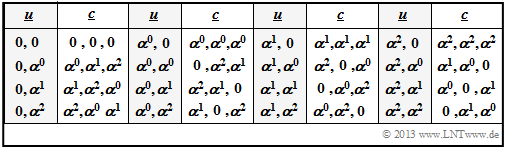
$\text{Beispiel 5:}$ Die Tabelle verdeutlicht die Bestimmung des Distanzspektrums für den $\text{RSC (3, 2, 2)}_4$.
- Gegenüber den bisherigen Grafiken wird die Symbolmenge vereinfachend mit $\{0,\ 1,\ 2,\ 3\}$ anstelle von $\{0,\ \alpha^0,\ \alpha^1,\ \alpha^2\}$ bezeichnet.
- Die Distanz $d$ zwischen $\underline {c}_j$ und dem Nullwort $\underline {c}_0$ ist identisch dem Hamming–Gewicht $w_{\rm H}(\underline {c}_j)$.
Aus der oberen Tabelle kann unter anderem abgelesen werden:
- Neun Codeworte unterscheiden sich vom Nullwort in zwei Symbolen und sechs Codeworte in drei Symbolen: $W_2 = 9$, $W_3 = 6$.
- Es gibt kein einziges Codewort mit nur einer Null. Das heißt: Die minimale Distanz beträgt hier $d_{\rm min} = 2$.
Aus der unteren Tabelle erkennt man, dass auch für die Binärdarstellung $d_{\rm min} = 2$ gilt.
Dieses empirische Ergebnis soll nun verallgemeinert werden:
$\text{Ohne Beweis:}$
- Die minimale Distanz eines jeden $(n, k)$–Reed–Solomon–Codes ist $d_{\rm min} =n-k+1$ ⇒ es lassen sich $e = d_{\rm min} -1 =n-k$ Symbolfehler erkennen.
- Bei fehlerkorrigierenden Codes wählt man meist $d_{\rm min} $ ungeradzahlig ⇒ $n-k$ geradzahlig. Bei RS–Codes können dann bis zu $t =(n-k)/2$ Symbolfehler korrigiert werden.
- Die Singleton–Schranke besagt, dass für alle linearen Codes $d_{\rm min} \le n-k+1$ gilt. RS–Codes erreichen diese Schranke mit Gleichheit; sie sind so genannte MDS–Codes (Maximum Distance Separable ).
- Das Distanzspektrum setzt sich zusammen aus $W_0 = 1$ sowie weiteren Gewichtsfaktoren $W_i$ mit $d ≤ i ≤ n$, wobei in der folgenden Gleichung $d_{\rm min}$ mit $d$ abgekürzt ist:
- \[W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \bigg [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \bigg ]\hspace{0.05cm}.\]
Codebezeichnung und Coderate
Die übliche Bezeichnung für die Reed–Solomon–Codes ist ${\rm RSC} \ \ (n,\ k, \ d_{\rm min})_q$ mit
- der Länge $n$ des Codes (Symbolanzahl eines Codewortes),
- der Dimension $k$ des Codes (Symbolanzahl eines Informationswortes),
- der minimalen Distanz $d_{\rm min} = n-k+1$, maximal entsprechend der Singleton–Schranke, und
- der Größe $q = 2^m$ des Galoisfeldes ${\rm GF}(q)$.
Alle Elemente $u_i$ des Informationswortes $\underline{u}= (u_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_{k-1})$ und alle Elemente ci des Codewortes $\underline{c}= (c_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_{n-1})$ sind nicht binäre Symbole und entstammen dem Galoisfeld ${\rm GF}(q)$.
Für die Realisierung werden diese Symbole stets auch binär dargestellt und man kommt zum äquivalenten binären Reed–Solomon–Code ${\rm RSC} \ \ (n_{\rm bin},\ k_{\rm bin}, \ d_{\rm min})_2$ mit
- $n_{\rm bin} = n \cdot m$ Bit eines Codewortes,
- $k_{\rm bin} = k \cdot m$ Bit eines Informationswortes.
Die Coderate wird durch diese Maßnahme nicht verändert:
- \[R_{\rm bin} = \frac{k_{\rm bin}}{n_{\rm bin}} = \frac{k \cdot m}{n \cdot m} = \frac{k}{n} = R \hspace{0.05cm}.\]
Ebenso ändert sich durch den Übergang von ${\rm GF}(q)$ auf ${\rm GF}(2)$ nichts an der minimalen Distanz $d_{\rm min}$.
$\text{Beispiel 6:}$ Wie im $\text{Beispiel 5}$ (vorherige Seite) betrachten wir wieder den $\text{RSC (3, 2, 2)}_4$ und geben dessen Distanzspektrum $\{ \hspace{0.05cm}W_j\hspace{0.05cm}\}$ nochmals an (obere Tabelle). Die untere Tabelle gilt für den äquivalenten binären Reed–Solomon–Code $\text{RSC (6, 4, 2)}_2$.
- Beide Codes haben die gleiche Coderate $R = k/n =2/3$ und auch die gleiche minimale Distanz $d_{\rm min} = 2$.
- Die beiden Codes unterscheiden sich jedoch hinsichtlich des Distanzspektrums $\{ \hspace{0.05cm}W_j\hspace{0.05cm}\}$ und der Gewichtsfunktion $W(X)$:
- $$\text{RSC (3, 2, 2)}_4\text{:} \hspace{0.3cm} W_0 = 1\hspace{0.05cm}, \hspace{0.2cm}W_2 = 9\hspace{0.05cm}, \hspace{0.2cm}W_3 = 6\hspace{0.3cm}\Rightarrow\hspace{0.3cm}W(X) = 1 + 9 \cdot X^2 + 6 \cdot X^3\hspace{0.05cm}.$$
- $$\text{RSC (6, 4, 2)}_2\text{:} \hspace{0.3cm} W_0 = 1\hspace{0.05cm}, \hspace{0.2cm}W_2 = 3\hspace{0.05cm}, \hspace{0.2cm}W_3 = 8 \hspace{0.05cm}, \hspace{0.2cm}W_4 = 3\hspace{0.05cm}, \hspace{0.2cm}W_6 = 1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}W(X) = 1 + 3 \cdot X^2 + 8 \cdot X^3 + 4 \cdot X^4 + X^6 \hspace{0.05cm}.$$
Bedeutung der Reed–Solomon–Codes
Anhand des hier oft beispielhaft betrachteten $\text{RSC (3, 2, 2)}_4$ konnten wir viele Eigenschaften der Reed–Solomon–Codes in überschaubarem Rahmen kennenlernen. Praxisrelevant ist dieser Code allerdings nicht, da wegen $d_{\rm min} = 2$ kein einziger Fehler korrigiert und auch nur ein einziger Fehler erkannt werden kann. Schon der nächstgrößere Code $\text{RSC (7, 3, 5)}_8$, der bis zu $t = 2$ Fehler korrigieren kann, weist bereits eine Codetabelle mit $8^3 = 512$ Einträgen auf und ist zu Demonstrationszwecken ungeeignet.
In der Praxis werden meist sehr große RS–Codes eingesetzt, zum Beispiel der $\text{RSC (255, 223, 33)}_{256}$ mit folgenden Eigenschaften:
- Der Code basiert auf dem Galoisfeld $\rm GF(2^8)$. Jedes Symbol entspricht somit einem Byte. Die Coderate ist mit $R = 0.8745$ relativ groß.
- Trotz dieser großen Coderate (also geringe Redundanz) können mit diesem Code bis zu $e = 32$ Fehler innerhalb eines Blocks aus $255$ Symbolen erkannt und $t = 16$ Fehler korrigiert werden.
- Die Codetabelle würde allerdings $2^{8 \hspace{0.05cm}\cdot \hspace{0.05cm} 223}= 2^{ \hspace{0.05cm} 1784} ≈ 10^{537}$ Einträge aufweisen und wird deshalb wahrscheinlich auch von niemanden tatsächlich erstellt.
Der große Vorteil der Reed–Solomon–Codes (und einer ganzen Reihe davon abgeleiteter weiterer Codes) ist zum einen, dass sie analytisch geschlossen konstruiert werden können, zum anderen ihre große Flexibilität hinsichtlich der Codeparameter. Meist geht man wie folgt vor:
- Man gibt die Korrekturfähigkeit in Form des Parameters $t$ vor. Daraus ergibt sich die minimale Distanz $d_{\rm min} = 2t + 1$ und die Differenz $n-k = 2t$ entsprechend der Singleton–Schranke. Einen besseren Wert gibt es nicht.
- Ein weiterer Entwurfsparameter ist die Coderate $R=k/n$, wobei die Codewortlänge $n = 2^m -1$ nicht völlig frei wählbar ist. Durch Erweiterung, Verkürzung und Punktierung – siehe Aufgabe 1.9Z – kann die Vielzahl an möglichen Codes weiter vergrößert werden.
- Bei Reed–Solomon–Codes ist die Gewichtsverteilung exakt bekannt und es ist eine Anpassung an die Fehlerstruktur des Kanals möglich. Diese Codes sind insbesondere für Bündelfehlerkanäle gut geeignet, die bei mobilen Funksystemen aufgrund von temporären Abschattungen häufig vorliegen.
- Im Falle statistisch unabhängiger Fehler sind BCH–Codes (von $\rm B$ose–$\rm C$haudhuri–$\rm H$ocquenghem) besser geeignet. Diese sind mit den RS–Codes eng verwandt, allerdings erfüllen sie nicht immer das Singleton–Kriterium. Eine ausführliche Beschreibung finden Sie in [Fri96][1].
- Die Decodierung nach dem BDD–Prinzip (Bounded Distance Decoding ) kann rechentechnisch sehr einfach erfolgen, zum Beispiel mit dem Berlekamp–Massey–Algorithmus. Zudem kann der Decoder ohne großen Mehraufwand auch Soft Decision Information verarbeiten.
Aufgaben zum Kapitel
Aufgabe 2.7: Reed–Solomon–Code (7, 3, 5) zur Basis 8
Aufgabe 2.7Z: Reed–Solomon–Code (15, 5, 11) zur Basis 16
Aufgabe 2.8: Generatorpolynome für Reed-Solomon
Aufgabe 2.8Z: „Plus” und „Mal” in GF(2 hoch 3)
Aufgabe 2.9: Reed–Solomon–Parameter
Aufgabe 2.10: Fehlererkennung bei Reed–Solomon
Aufgabe 2.10Z: Coderate und minimale Distanz
Quellenverzeichnis
- ↑ Friedrichs, B.: Kanalcodierung – Grundlagen und Anwendungen in modernen Kommunikations- systemen. Berlin – Heidelberg: Springer, 1996.