Difference between revisions of "Exercise 2.3Z: xDSL Frequency Band"
| (15 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/xDSL_as_Transmission_Technology |
}} | }} | ||
| − | [[File:P_ID1969__Bei_Z_2_3.png|right|frame| | + | [[File:P_ID1969__Bei_Z_2_3.png|right|frame|xDSL frequency band allocation]] |
| − | + | The figure shows the frequency band allocation of a common $\rm xDSL$ system: | |
| + | *The ISDN band is located at the bottom. | ||
| + | *Two bands follow $\rm A$ and $\rm B$, representing downstream and upstream. | ||
| + | *Nothing is said about the order of the two bands. This is the question for subtask '''(2)'''. | ||
| − | |||
| − | + | Further it is standardized with xDSL/DMT that. | |
| − | |||
| − | |||
| − | |||
| − | + | *$4000$ frames are transmitted per second, | |
| + | *a synchronization frame is inserted after every $68$ data frames, | ||
| + | *the symbol duration must be shortened by the factor $16/17$ because of the cyclic prefix, | ||
| + | *each data frame is encoded to a DMT symbol. | ||
| − | |||
| − | + | This also determines the integration duration $T$ which is evaluated at the receiver for detection, and at the same time also represents the fundamental frequency $f_{0} = 1/T$ of the DMT (''Discrete Multitone Transmission'') method considered here. | |
| Line 25: | Line 26: | ||
| − | === | + | Hint: |
| + | |||
| + | *This exercise refers to the chapter [[Examples_of_Communication_Systems/xDSL_as_Transmission_Technology|"xDSL as Transmission Technology"]]. | ||
| + | *For information on the ''cyclic prefix'', refer to the chapter [[Examples_of_Communication_Systems/Methods_to_Reduce_the_Bit_Error_Rate_in_DSL|"Methods to Reduce the Bit Error Rate in DSL"]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | { What $\rm xDSL$ system is it? |
| − | |type=" | + | |type="()"} |
- ADSL, | - ADSL, | ||
+ ADSL2+, | + ADSL2+, | ||
- VDSL. | - VDSL. | ||
| − | { | + | { What is the order of upstream and downstream? |
| − | |type=" | + | |type="()"} |
| − | + $A$ | + | + $\rm A$ identifies the upstream and $\rm B$ the downstream. |
| − | - $A$ | + | - $\rm A$ denotes the downstream and $\rm B$ the upstream. |
| − | + | { What symbol duration $T$ results for the DMT system? | |
| − | { | ||
|type="{}"} | |type="{}"} | ||
| − | $T \ = \ ${ 232 3% } $\ | + | $T \ = \ ${ 232 3% } $\ \rm µ s$ |
| − | { | + | { What is the fundamental frequency $ f_{0}$ underlying the DMT process? |
|type="{}"} | |type="{}"} | ||
$ f_{0} \ = \ ${ 4.3125 3% } $\ \rm kHz$ | $ f_{0} \ = \ ${ 4.3125 3% } $\ \rm kHz$ | ||
| − | { | + | { How many channels $(\hspace{-0.03cm}K_{\rm max}\hspace{-0.03cm})$ could be transmitted in $2208 \ \rm kHz$ ? |
|type="{}"} | |type="{}"} | ||
| − | $ K_{\rm max} \ = \ ${ 512 | + | $ K_{\rm max} \ = \ ${ 512 } |
| − | { | + | { How many downstream channels $(\hspace{-0.03cm}K_{\rm down}\hspace{-0.03cm})$ result in this system, given the omission of lower frequencies? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $K_{\rm down} \ = \ ${ 448 } |
| − | { | + | { With how many bits $(b)$ would the bins have to be occupied on average ⇒ ${\rm E}\big [ \hspace{0.05cm} b \hspace{0.05cm}\big ]$ so that the bit rate $R_{\rm B} = 25 \ \rm Mbit/s$ is? |
|type="{}"} | |type="{}"} | ||
| − | $ b \ = \ ${ | + | $ {\rm E}\big [ \hspace{0.05cm} b \hspace{0.05cm}\big ] \ = \ ${ 13.95 3% } $\ \rm bit$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is <u>the second proposed solution</u>: |
| + | *For ADSL2+, the frequency band ends at $2208 \rm kHz$ as shown in the sketch. | ||
| + | *For ADSL, the frequency band already ends at $1104 \rm kHz$. | ||
| + | *VDSL has a much larger bandwidth, depending on the band plan, with upstream and downstream bands alternating in each case. | ||
| + | |||
| + | |||
| + | '''(2)''' Correct is <u>the first proposed solution</u>: | ||
| + | *The upstream was assigned the better (lower) frequencies, since a loss of the fewer upstream channels has a less favorable percentage effect than a loss of a downstream channel. | ||
| + | |||
| + | |||
| + | '''(3)''' Without taking into account the synchronization frames (after every $68$ of frames occupied with user data) and the guard interval, the frame duration would result in | ||
| + | :$$T = 1/(4000/{\rm s}) = 250 \ \rm µ s.$$ | ||
| + | *With this overhead taken into account, the symbol duration is shorter by a factor of $68/69 \cdot 16/17$: | ||
| + | :$$T = \frac{68}{69} \cdot \frac{16}{17} \cdot 250\, {\rm \mu s} \hspace{0.15cm}\underline{ \approx 232\, {\rm µ s}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' The subcarriers lie at DMT at all multiples of $f_0$, where must hold: | ||
| + | :$$f_0 = \frac{1}{T} \hspace{0.15cm}\underline{= 4.3125 \, {\rm kHz}}.$$ | ||
| + | |||
| + | *In fact, the time windowing corresponds to the multiplication of the cosine carrier signals by a square wave function of duration $T$. | ||
| + | *In the frequency domain, this results in the convolution with the si function. | ||
| + | *If the system quantities $T$ and $f_0 = 1/T$ were not tuned to each other, a ''de-orthogonalization'' of the individual DMT channels and thus ''intercarrier interference'' would occur. | ||
| + | |||
| + | |||
| + | '''(5)''' Ignoring ISDN/upstream reservation, we get $K_{\rm max} = 2208/4.3125 \underline{= 512}.$ | ||
| + | |||
| + | |||
| + | '''(6)''' The lower $276/4.3125 = 64$ channels are reserved for ISDN and upstream in the "ADSL2+" system considered here. | ||
| + | * This leaves $K_{\rm down} = 512 - 64\hspace{0.15cm} \underline{= 448}$ usable channels. | ||
| + | |||
| + | |||
| + | '''(7)''' For the bitrate holds. | ||
| + | :$$R_{\rm B} = 4000 \, \,\frac {\rm frame}{\rm s} \cdot K \cdot b \hspace{0.05cm}.$$ | ||
| + | *This results in the (average) bit allocation per bin: | ||
| + | :$${\rm E}\big [ \hspace{0.05cm} b \hspace{0.05cm}\big ] = \frac{R_{\rm B}}{ 4000 \, \, {\rm frame}/{\rm s} \cdot K} = \frac{25 \cdot 10^6 \,\, {\rm bit/s}}{ 4000 \, \, {1}/{\rm s} \cdot 448} \hspace{0.15cm}\underline{= 13.95 \, \, {\rm bit}}\hspace{0.05cm}.$$ | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 71: | Line 116: | ||
| − | [[Category: | + | [[Category:Examples of Communication Systems: Exercises|^2.3 xDSL Transmission Technology |
^]] | ^]] | ||
Latest revision as of 17:19, 7 March 2023
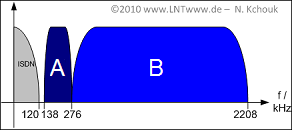
The figure shows the frequency band allocation of a common $\rm xDSL$ system:
- The ISDN band is located at the bottom.
- Two bands follow $\rm A$ and $\rm B$, representing downstream and upstream.
- Nothing is said about the order of the two bands. This is the question for subtask (2).
Further it is standardized with xDSL/DMT that.
- $4000$ frames are transmitted per second,
- a synchronization frame is inserted after every $68$ data frames,
- the symbol duration must be shortened by the factor $16/17$ because of the cyclic prefix,
- each data frame is encoded to a DMT symbol.
This also determines the integration duration $T$ which is evaluated at the receiver for detection, and at the same time also represents the fundamental frequency $f_{0} = 1/T$ of the DMT (Discrete Multitone Transmission) method considered here.
Hint:
- This exercise refers to the chapter "xDSL as Transmission Technology".
- For information on the cyclic prefix, refer to the chapter "Methods to Reduce the Bit Error Rate in DSL".
Questions
Solution
- For ADSL2+, the frequency band ends at $2208 \rm kHz$ as shown in the sketch.
- For ADSL, the frequency band already ends at $1104 \rm kHz$.
- VDSL has a much larger bandwidth, depending on the band plan, with upstream and downstream bands alternating in each case.
(2) Correct is the first proposed solution:
- The upstream was assigned the better (lower) frequencies, since a loss of the fewer upstream channels has a less favorable percentage effect than a loss of a downstream channel.
(3) Without taking into account the synchronization frames (after every $68$ of frames occupied with user data) and the guard interval, the frame duration would result in
- $$T = 1/(4000/{\rm s}) = 250 \ \rm µ s.$$
- With this overhead taken into account, the symbol duration is shorter by a factor of $68/69 \cdot 16/17$:
- $$T = \frac{68}{69} \cdot \frac{16}{17} \cdot 250\, {\rm \mu s} \hspace{0.15cm}\underline{ \approx 232\, {\rm µ s}} \hspace{0.05cm}.$$
(4) The subcarriers lie at DMT at all multiples of $f_0$, where must hold:
- $$f_0 = \frac{1}{T} \hspace{0.15cm}\underline{= 4.3125 \, {\rm kHz}}.$$
- In fact, the time windowing corresponds to the multiplication of the cosine carrier signals by a square wave function of duration $T$.
- In the frequency domain, this results in the convolution with the si function.
- If the system quantities $T$ and $f_0 = 1/T$ were not tuned to each other, a de-orthogonalization of the individual DMT channels and thus intercarrier interference would occur.
(5) Ignoring ISDN/upstream reservation, we get $K_{\rm max} = 2208/4.3125 \underline{= 512}.$
(6) The lower $276/4.3125 = 64$ channels are reserved for ISDN and upstream in the "ADSL2+" system considered here.
- This leaves $K_{\rm down} = 512 - 64\hspace{0.15cm} \underline{= 448}$ usable channels.
(7) For the bitrate holds.
- $$R_{\rm B} = 4000 \, \,\frac {\rm frame}{\rm s} \cdot K \cdot b \hspace{0.05cm}.$$
- This results in the (average) bit allocation per bin:
- $${\rm E}\big [ \hspace{0.05cm} b \hspace{0.05cm}\big ] = \frac{R_{\rm B}}{ 4000 \, \, {\rm frame}/{\rm s} \cdot K} = \frac{25 \cdot 10^6 \,\, {\rm bit/s}}{ 4000 \, \, {1}/{\rm s} \cdot 448} \hspace{0.15cm}\underline{= 13.95 \, \, {\rm bit}}\hspace{0.05cm}.$$