Difference between revisions of "Exercise 2.6: Cyclic Prefix"
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| (11 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/Methods_to_Reduce_the_Bit_Error_Rate_in_DSL |
}} | }} | ||
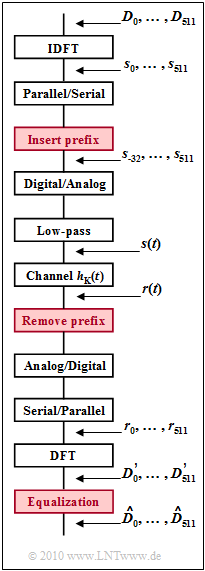
| − | [[File: | + | [[File:EN_Bei_A_2_6.png|right|frame|$\rm DSL/DMT$ realization with cyclic prefix]] |
| + | A major advantage of $\rm DSL/DMT$ is the simple equalization of channel distortion by inserting a guard interval and a cyclic prefix. The diagram shows a simplified block diagram, where the prefix used for equalization of the channel frequency response | ||
| + | :$$H_{\rm K}(f) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm K}(t)$$ | ||
| + | |||
| + | required components are highlighted in red. | ||
| + | |||
| + | For the $\rm ADSL/DMT$ downstream the following parameters apply: | ||
| − | + | *With each frame, the subchannels $k = 64$, ... , $255$ at the carrier frequencies $f_k = k \cdot f_0$ occupied with the QAM symbols $D_k$ . Because of the reservation of the lowest frequencies for ISDN and for upstream $D_0 =$ ... $= D_{63} = 0$. | |
| − | |||
| − | + | *The fundamental frequency is chosen to $f_0 = 4.3125 \ \rm kHz$ and the frame duration is $T = 1/f_0 \approx 232 \ {\rm µ s}$. These values result from the requirement that $4000$ frames should be transmitted per second and a synchronization frame is inserted after every $68$–th frame. | |
| − | + | *After occupying the upper coefficients $(k = 257$, ... , $448)$ according to $D_k = D_{512-k}^{\ast}$ the entire block $D_0$, ... , $D_{511}$ is fed to an ''Inverse Discrete Fourier Transform'' $\rm (IDFT)$ . The time coefficients are then $s_0$, ... , $s_{511}$. | |
| − | * | + | *To avoid impulse interference - also called ''inter-symbol interference'' $\rm (ISI)$ - between adjacent frames, a guard interval of duration $T_{\rm G}$ is inserted between two frames. The frame spacing must be at least as large as the "length" $T_{\rm K}$ of the impulse response. |
| − | * | + | *In addition, the IDFT output values $(s_{480}$, ... , $s_{511})$ are duplicated, prefixed as $(s_{-32}$, ... , $s_{-1})$ to the output vector $(s_0$, ... , $s_{511})$ and transmitted in the guard interval. This is called the "cyclic prefix". Thus, the subcarriers of a frame do not interfere with each other either, which means that there is not only no $\rm ISI$, but also no inter-carrier interference $\rm (ICI)$. |
| − | |||
| − | |||
| − | |||
| Line 29: | Line 31: | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Examples_of_Communication_Systems/Methods_to_Reduce_the_Bit_Error_Rate_in_DSL|"Methods to Reduce the Bit Error Rate in DSL"]]. |
| − | * | + | *Reference is made in particular to the page [[Examples_of_Communication_Systems/Methods_to_Reduce_the_Bit_Error_Rate_in_DSL#Inserting_guard_interval_and_cyclic_prefix|"Inserting guard interval and cyclic prefix"]]. |
| − | * | + | *In the questions $s_k(t)$ denotes the (continuous-time) waveform when only the coefficient $D_k$ of the carrier at $f_k = k \cdot f_0$ is different from zero. |
| Line 38: | Line 40: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What should be the duration $T_{\rm G}$ of the guard interval? |
|type="{}"} | |type="{}"} | ||
$T_{\rm G} \ = \ ${ 14.5 3% } $ \ \rm µ s$ | $T_{\rm G} \ = \ ${ 14.5 3% } $ \ \rm µ s$ | ||
| − | { | + | {What extent $(T_{\rm K, \ max} )$ may the channel impulse response $h_{\rm K}(t)$ have so that there is no intersymbol interference? |
|type="{}"} | |type="{}"} | ||
$T_{\rm K, \ max} \ = \ ${ 14.5 3% } $ \ \rm µ s$ | $T_{\rm K, \ max} \ = \ ${ 14.5 3% } $ \ \rm µ s$ | ||
| − | { | + | {What are the properties of the DMT system with cyclic prefix? The influence of the noise shall be disregarded here. |
| − | |type=" | + | |type="()"} |
| − | - | + | - All spectral coefficients after DFT $(D_k\hspace{0.01cm}')$ are equal $D_k$. |
| − | + | + | + The coefficients after equalization $(\hat{D}_k)$ are equal $D_k$. |
| − | - | + | - The guard interval has no effect on the data rate. |
| − | { | + | {What if the guard interval is left unassigned? |
| − | |type=" | + | |type="()"} |
| − | - | + | - This would not improve anything. |
| − | + | + | + Data of different frames do not interfere with each other. |
| − | - | + | - Data within a frame does not interfere with each other. |
| − | { | + | {On what principle is the cyclic prefix based? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The influence of $h_K(t)$ is limited to the range $t < 0$ . |
| − | + | + | + For $0 ≤ t ≤ T$ represents $s_k(t)$ a harmonic oscillation. |
| − | - $h_{\rm K}(t)$ | + | - $h_{\rm K}(t)$ has no influence on magnitude and phase of $s_k(t)$. |
| Line 77: | Line 79: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Within the guard interval, additional samples $s_{-32}$, ... must be inserted at sender $32$. , $s_{-1}$ must be inserted. Thus: |
:$$T_{\rm G} = \frac{32}{512} \cdot T = \frac{232\,{\rm µ s}}{16} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s} }\hspace{0.05cm}.$$ | :$$T_{\rm G} = \frac{32}{512} \cdot T = \frac{232\,{\rm µ s}}{16} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s} }\hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' Intersymbol interference (ISI) and intercarrier interference (ICI) are avoided as long as the length $T_{\rm K}$ of the channel impulse response is not greater than the length $T_{\rm G}$ of the guard interval: |
:$$T_{\rm K,\hspace{0.08cm} max} \le T_{\rm G} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s}} \hspace{0.05cm}.$$ | :$$T_{\rm K,\hspace{0.08cm} max} \le T_{\rm G} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s}} \hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | '''(3)''' The correct solution is <u>proposed solution 2</u>. |
| − | * | + | *For the output coefficients of the DFT, in the noise-free case: |
:$$D_k\hspace{0.01cm}' = D_k \cdot H_{\rm K} ( f = f_k), \hspace{0.2cm} f_k = k \cdot f_0 \hspace{0.05cm}.$$ | :$$D_k\hspace{0.01cm}' = D_k \cdot H_{\rm K} ( f = f_k), \hspace{0.2cm} f_k = k \cdot f_0 \hspace{0.05cm}.$$ | ||
| − | * | + | *The individual bins can be equalized individually by multiplying by $H_{\rm K}^{-1}(f = f_k)$. Thus, for all $k = 1$, ... , $K$: |
:$$\hat{D}_k = D_k \hspace{0.05cm}.$$ | :$$\hat{D}_k = D_k \hspace{0.05cm}.$$ | ||
| − | * | + | *Statement 3 is false: rather, the rate is lower by a factor of $T/(T + T_{\rm G}) = 16/17$ than without guard interval and cyclic prefix. |
| − | * | + | *However, this small loss is readily accepted, since the ease of equalization more than compensates for this disadvantage. |
| + | |||
| + | |||
| + | '''(4)''' Correct here is only the <u>proposed solution 2</u>: | ||
| + | *This would not prevent so-called intercarrier interference, that is, the subcarriers of a frame would then no longer be orthogonal to each other, since the convolution of the harmonic oscillation limited in time to $T$ with the impulse response does not yield an si function, as is the case with [[Examples_of_Communication_Systems/xDSL_as_Transmission_Technology#Basics_of_DMT_-_Discrete_Multitone_Transmission|"ideal channel"]]. | ||
| + | *Thus, the coefficient $D_k$ at $k \cdot f_0$ also affects the spectral values at $\kappa \cdot f_0$ in the neighborhood $(\kappa \neq k)$. | ||
| − | |||
| − | |||
| − | |||
| − | '''(5)''' | + | '''(5)''' The correct <u>solutions 1 and 2</u> are: |
| − | * | + | *The magnitude and phase of $s_k(t)$ is very well changed by $h_{\rm K}(t)$, corresponding to the value $H_{\rm K}(f = f_k)$ of the frequency response. |
| − | * | + | *However, this error can be corrected in a simple way (and independently of the other bins) by the equalizer on the receiver side. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 109: | Line 113: | ||
| − | [[Category: | + | [[Category:Examples of Communication Systems: Exercises|^2.4 BER Lowering at DSL |
^]] | ^]] | ||
Latest revision as of 18:37, 25 March 2023
A major advantage of $\rm DSL/DMT$ is the simple equalization of channel distortion by inserting a guard interval and a cyclic prefix. The diagram shows a simplified block diagram, where the prefix used for equalization of the channel frequency response
- $$H_{\rm K}(f) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm K}(t)$$
required components are highlighted in red.
For the $\rm ADSL/DMT$ downstream the following parameters apply:
- With each frame, the subchannels $k = 64$, ... , $255$ at the carrier frequencies $f_k = k \cdot f_0$ occupied with the QAM symbols $D_k$ . Because of the reservation of the lowest frequencies for ISDN and for upstream $D_0 =$ ... $= D_{63} = 0$.
- The fundamental frequency is chosen to $f_0 = 4.3125 \ \rm kHz$ and the frame duration is $T = 1/f_0 \approx 232 \ {\rm µ s}$. These values result from the requirement that $4000$ frames should be transmitted per second and a synchronization frame is inserted after every $68$–th frame.
- After occupying the upper coefficients $(k = 257$, ... , $448)$ according to $D_k = D_{512-k}^{\ast}$ the entire block $D_0$, ... , $D_{511}$ is fed to an Inverse Discrete Fourier Transform $\rm (IDFT)$ . The time coefficients are then $s_0$, ... , $s_{511}$.
- To avoid impulse interference - also called inter-symbol interference $\rm (ISI)$ - between adjacent frames, a guard interval of duration $T_{\rm G}$ is inserted between two frames. The frame spacing must be at least as large as the "length" $T_{\rm K}$ of the impulse response.
- In addition, the IDFT output values $(s_{480}$, ... , $s_{511})$ are duplicated, prefixed as $(s_{-32}$, ... , $s_{-1})$ to the output vector $(s_0$, ... , $s_{511})$ and transmitted in the guard interval. This is called the "cyclic prefix". Thus, the subcarriers of a frame do not interfere with each other either, which means that there is not only no $\rm ISI$, but also no inter-carrier interference $\rm (ICI)$.
Hints:
- This exercise belongs to the chapter "Methods to Reduce the Bit Error Rate in DSL".
- Reference is made in particular to the page "Inserting guard interval and cyclic prefix".
- In the questions $s_k(t)$ denotes the (continuous-time) waveform when only the coefficient $D_k$ of the carrier at $f_k = k \cdot f_0$ is different from zero.
Questions
Solution
- $$T_{\rm G} = \frac{32}{512} \cdot T = \frac{232\,{\rm µ s}}{16} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s} }\hspace{0.05cm}.$$
(2) Intersymbol interference (ISI) and intercarrier interference (ICI) are avoided as long as the length $T_{\rm K}$ of the channel impulse response is not greater than the length $T_{\rm G}$ of the guard interval:
- $$T_{\rm K,\hspace{0.08cm} max} \le T_{\rm G} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s}} \hspace{0.05cm}.$$
(3) The correct solution is proposed solution 2.
- For the output coefficients of the DFT, in the noise-free case:
- $$D_k\hspace{0.01cm}' = D_k \cdot H_{\rm K} ( f = f_k), \hspace{0.2cm} f_k = k \cdot f_0 \hspace{0.05cm}.$$
- The individual bins can be equalized individually by multiplying by $H_{\rm K}^{-1}(f = f_k)$. Thus, for all $k = 1$, ... , $K$:
- $$\hat{D}_k = D_k \hspace{0.05cm}.$$
- Statement 3 is false: rather, the rate is lower by a factor of $T/(T + T_{\rm G}) = 16/17$ than without guard interval and cyclic prefix.
- However, this small loss is readily accepted, since the ease of equalization more than compensates for this disadvantage.
(4) Correct here is only the proposed solution 2:
- This would not prevent so-called intercarrier interference, that is, the subcarriers of a frame would then no longer be orthogonal to each other, since the convolution of the harmonic oscillation limited in time to $T$ with the impulse response does not yield an si function, as is the case with "ideal channel".
- Thus, the coefficient $D_k$ at $k \cdot f_0$ also affects the spectral values at $\kappa \cdot f_0$ in the neighborhood $(\kappa \neq k)$.
(5) The correct solutions 1 and 2 are:
- The magnitude and phase of $s_k(t)$ is very well changed by $h_{\rm K}(t)$, corresponding to the value $H_{\rm K}(f = f_k)$ of the frequency response.
- However, this error can be corrected in a simple way (and independently of the other bins) by the equalizer on the receiver side.