Difference between revisions of "Aufgaben:Exercise 2.12: Non-coherent Demodulation"
m (Guenter verschob die Seite 2.13 Zur nichtkohärenten Demodulation nach 2.12 Zur nichtkohärenten Demodulation) |
|||
| (26 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation Methods/Further AM Variants |
}} | }} | ||
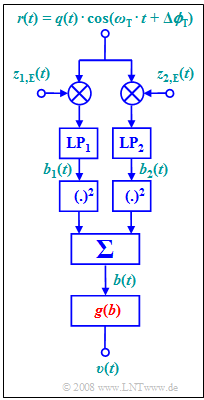
| − | [[File: | + | [[File:EN_Mod_A_2_12.png|right|frame|ASK Demodulation <br>(non-coherent) ]] |
| − | + | Consider an amplitude modulated signal: | |
| − | $$ s(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$ | + | :$$ s(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$ |
| − | + | Reaching the receiver based on the channel propagation time, the signal is | |
| − | $$ r(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \hspace{0.05cm}.$$ | + | :$$ r(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \hspace{0.05cm}.$$ |
| − | + | The arrangement shown here allows perfect demodulation – that is: $v(t) = q(t)$ – without knowledge of the phase $Δϕ_T$, but only if the source signal $q(t)$ satisfies certain conditions. | |
| − | + | The two receiver-side carrier signals are: | |
| − | $$ z_{\rm 1, \hspace{0.08cm}E}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm},$$ | + | :$$ z_{\rm 1, \hspace{0.08cm}E}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm},$$ |
| − | $$ z_{\rm 2, \hspace{0.08cm}E}(t) = -2 \cdot \sin(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$ | + | :$$ z_{\rm 2, \hspace{0.08cm}E}(t) = -2 \cdot \sin(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$ |
| − | $ | + | $\rm LP_1$ and $\rm LP_2$ denote two ideal (rectangular) low-pass filters, each with cutoff frequency equal to the carrier frequency $f_{\rm T}$. |
| − | + | We consider as (digital) source signals: | |
| − | + | # the unipolar square wave signal $q_1(t)$ with dimensionless amplitude values $0$ and $3$, | |
| − | + | # the bipolar square wave signal $q_2(t)$ with the dimensionless amplitude values $±3$. | |
| − | |||
| − | + | With respect to $s(t)$, these two signals result in | |
| − | $$ \cos(\alpha) \cdot \cos(\beta) = | + | #an [[Modulation_Methods/Linear_Digital_Modulation#ASK_.E2.80.93_Amplitude_Shift_Keying|ASK signal]], |
| − | $$ \sin(\alpha) \cdot \sin(\beta) = | + | #a [[Modulation_Methods/Linear_Digital_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|BPSK signal]]. |
| − | $$ \sin(\alpha) \cdot \cos(\beta) = | + | |
| − | === | + | |
| + | The nonlinear function $v = g(b)$ is to be determined in this exercise. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *This exercise belongs to the chapter [[Modulation_Methods/Further_AM_Variants|Further AM Variants]]. | ||
| + | *Particular reference is made to the section [[Modulation_Methods/Further_AM_Variants#Incoherent_.28non-coherent.29_Demodulation|Incoherent (non-coherent) Demodulation]]. | ||
| + | |||
| + | *The following trigonometric transformations are given: | ||
| + | :$$ \cos(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \big],$$ | ||
| + | :$$ \sin(\alpha) \cdot \sin(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \big],$$ | ||
| + | :$$ \sin(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \big] \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the signals $b_1(t)$ and $b_2(t)$ in both branches – after multiplier and low-pass respectively? Which statements apply? |
|type="[]"} | |type="[]"} | ||
| − | + $b_1(t) = q(t) · cos( | + | + $b_1(t) = q(t) · \cos(Δϕ_{\rm T})$. |
| − | - $b_2(t) = q(t) · cos( | + | - $b_2(t) = q(t) · \cos(Δϕ_{\rm T})$. |
| − | - $b_1(t) = q(t) · sin( | + | - $b_1(t) = q(t) · \sin(Δϕ_{\rm T})$. |
| − | + $b_2(t) = q(t) · sin( | + | + $b_2(t) = q(t) · \sin(Δϕ_{\rm T})$. |
| − | - $b_2(t) = q(t | + | - $b_1(t) = b_2(t) = q(t)$. |
| − | { | + | {What values of $b_{\rm min}$ and $b_{\rm max}$ does the signal $b(t)$ take on, when the unipolar source signal $q_1(t)$ is applied to the input? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $b_{\rm min} \ = \ $ { 0. } |
| − | $ | + | $b_{\rm max} \ = \ $ { 9 3% } |
| − | { | + | {How should the characteristic curve $v = g(b)$ be chosen, so that $v(t) = q(t)$ holds? |
| − | |type=" | + | |type="()"} |
| − | - $g(b) = b^2$. | + | - $v=g(b) = b^2$. |
| − | + $g(b) = b | + | + $v=g(b) = \sqrt{b}$. |
| − | - $g(b) = arctan(b).$ | + | - $v=g(b) = \arctan(b).$ |
| − | { | + | {What values of $b_{\rm min}$ and $b_{\rm max}$ does the signal $b(t)$ take on, when the bipolar source signal $q_2(t)$ is applied to the input? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $b_{\rm min} \ = \ $ { 9 3% } |
| − | $ | + | $b_{\rm max} \ = \ $ { 9 3% } |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Applying the trigonometric transformations given on the exercise page and taking into account the two low-pass filters (the components around twice the carrier frequency are removed), we obtain: |
| − | $$b_1(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \cdot 2 \cdot \cos(\omega_{\rm T} \cdot t) = q(t) \cdot \cos(\Delta \phi_{\rm T})\hspace{0.05cm},$$ | + | :$$b_1(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \cdot 2 \cdot \cos(\omega_{\rm T} \cdot t) = q(t) \cdot \cos(\Delta \phi_{\rm T})\hspace{0.05cm},$$ |
| − | $$ b_2(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \cdot (-2) \cdot \sin(\omega_{\rm T} \cdot t) = q(t) \cdot \sin(\Delta \phi_{\rm T})\hspace{0.05cm}.$$ | + | :$$ b_2(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \cdot (-2) \cdot \sin(\omega_{\rm T} \cdot t) = q(t) \cdot \sin(\Delta \phi_{\rm T})\hspace{0.05cm}.$$ |
| − | + | *Thus, <u>the first and fourth answers</u> are correct. | |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' The sum of the squares of the two partial signals gives: | ||
| + | :$$ b(t) = b_1^2(t) + b_2^2(t)= q^2(t) \cdot \left( \cos^2(\Delta \phi_{\rm T})+ \sin^2(\Delta \phi_{\rm T})\right) = q^2(t)\hspace{0.05cm}.$$ | ||
| + | The possible amplitude values are thus: | ||
| + | :$$b_{\rm min}\hspace{0.15cm}\underline{ = 0},$$ | ||
| + | :$$ b_{\rm max}\hspace{0.15cm}\underline{ =9}.$$ | ||
| − | |||
| − | |||
| − | |||
| + | '''(3)''' The <u>second answer</u> is correct: | ||
| + | :$$v=g(b) = \sqrt{b} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t) = \sqrt{ q^2(t) } = q(t)\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| + | '''(4)''' The result $b(t) = q^2(t)$ – see subtask '''(2)''' – leads here to the result: | ||
| + | :$$b_{\rm min}\hspace{0.15cm}\underline{ = 9},$$ | ||
| + | :$$b_{\rm max}\hspace{0.15cm}\underline{ =9}.$$ | ||
| − | + | This shows that the demodulator considered here only functions, | |
| + | *if at all times $q(t) ≥ 0$ or $q(t) ≤ 0$ holds, | ||
| + | *and this is known at the receiver. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 80: | Line 106: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^2.5 Other AM Variants^ ]] |
Latest revision as of 13:46, 17 November 2022
Consider an amplitude modulated signal:
- $$ s(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$
Reaching the receiver based on the channel propagation time, the signal is
- $$ r(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \hspace{0.05cm}.$$
The arrangement shown here allows perfect demodulation – that is: $v(t) = q(t)$ – without knowledge of the phase $Δϕ_T$, but only if the source signal $q(t)$ satisfies certain conditions.
The two receiver-side carrier signals are:
- $$ z_{\rm 1, \hspace{0.08cm}E}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm},$$
- $$ z_{\rm 2, \hspace{0.08cm}E}(t) = -2 \cdot \sin(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$
$\rm LP_1$ and $\rm LP_2$ denote two ideal (rectangular) low-pass filters, each with cutoff frequency equal to the carrier frequency $f_{\rm T}$.
We consider as (digital) source signals:
- the unipolar square wave signal $q_1(t)$ with dimensionless amplitude values $0$ and $3$,
- the bipolar square wave signal $q_2(t)$ with the dimensionless amplitude values $±3$.
With respect to $s(t)$, these two signals result in
- an ASK signal,
- a BPSK signal.
The nonlinear function $v = g(b)$ is to be determined in this exercise.
Hints:
- This exercise belongs to the chapter Further AM Variants.
- Particular reference is made to the section Incoherent (non-coherent) Demodulation.
- The following trigonometric transformations are given:
- $$ \cos(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \big],$$
- $$ \sin(\alpha) \cdot \sin(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \big],$$
- $$ \sin(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \big] \hspace{0.05cm}.$$
Questions
Solution
- $$b_1(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \cdot 2 \cdot \cos(\omega_{\rm T} \cdot t) = q(t) \cdot \cos(\Delta \phi_{\rm T})\hspace{0.05cm},$$
- $$ b_2(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \cdot (-2) \cdot \sin(\omega_{\rm T} \cdot t) = q(t) \cdot \sin(\Delta \phi_{\rm T})\hspace{0.05cm}.$$
- Thus, the first and fourth answers are correct.
(2) The sum of the squares of the two partial signals gives:
- $$ b(t) = b_1^2(t) + b_2^2(t)= q^2(t) \cdot \left( \cos^2(\Delta \phi_{\rm T})+ \sin^2(\Delta \phi_{\rm T})\right) = q^2(t)\hspace{0.05cm}.$$
The possible amplitude values are thus:
- $$b_{\rm min}\hspace{0.15cm}\underline{ = 0},$$
- $$ b_{\rm max}\hspace{0.15cm}\underline{ =9}.$$
(3) The second answer is correct:
- $$v=g(b) = \sqrt{b} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t) = \sqrt{ q^2(t) } = q(t)\hspace{0.05cm}.$$
(4) The result $b(t) = q^2(t)$ – see subtask (2) – leads here to the result:
- $$b_{\rm min}\hspace{0.15cm}\underline{ = 9},$$
- $$b_{\rm max}\hspace{0.15cm}\underline{ =9}.$$
This shows that the demodulator considered here only functions,
- if at all times $q(t) ≥ 0$ or $q(t) ≤ 0$ holds,
- and this is known at the receiver.