Difference between revisions of "Applets:Attenuation of Copper Cables"
| (58 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{LntAppletLinkEn|attenuationCopperCables_en}} [https://www.lntwww.de/Applets:Dämpfung_von_Kupferkabeln '''English Applet with German WIKI description'''] |
==Applet Description== | ==Applet Description== | ||
<br> | <br> | ||
| + | This applet calculates the attenuation function $a_{\rm K}(f)$ of conducted transmission media $($with cable length $l)$: | ||
| + | *For coaxial cables one usually uses the equation $a_{\rm K}(f)=(\alpha_0+\alpha_1\cdot f+\alpha_2\cdot \sqrt{f}) \cdot l$. | ||
| + | |||
| + | *In contrast, two-wire lines are often displayed in the form $a_{\rm K}(f)=(k_1+k_2\cdot (f/{\rm MHz})^{k_3}) \cdot l$. | ||
| + | |||
| + | *The conversion of the $(k_1, \ k_2, \ k_3)$ parameters to the $(\alpha_0, \ \alpha_1, \ \alpha_2)$ parameters for $B = 30 \ \rm MHz$ is realized as well as the other way around. | ||
| + | |||
| + | |||
| + | Aside from the attenuation function $a_{\rm K}(f)$ the applet can display: | ||
| + | *the associated magnitude frequency response $\left | H_{\rm K}(f)\right |=10^{-a_\text{K}(f)/20},$ | ||
| + | |||
| + | *the equalizer frequency response $\left | H_{\rm E}(f)\right | = \left | H_{\rm CRO}(f) / H_{\rm K}(f)\right | $, that leads to a Nyquist total frequency response $ H_{\rm CRO}(f) $, | ||
| + | |||
| + | *the corresponding squared magnitude frequency response $\left | H_{\rm E}(f)\right |^2 $. | ||
| + | |||
| + | |||
| + | The integral over $\left | H_{\rm E}(f)\right |^2 $ is a measure of the noise exaggeration of the selected Nyquist total frequency response and thus also for the expected error probability. From this, the »total efficiency« $\eta_\text{K+E}$ for the channel $($German: '''K'''anal$)$ plus the equalizer $($German: '''E'''ntzerrer$)$ is calculated, which in the applet is output in $\rm dB$. | ||
| + | |||
| + | Through optimization of the roll-off factor $r$ of the raised cosine frequency response $ H_{\rm CRO}(f) $ one gets the »channel efficiency« $ \eta_\text{K}$. This value indicates the deterioration of the overall system due to the attenuation function $ a_{\rm K} (f) $ of the transmission medium. | ||
==Theoretical Background== | ==Theoretical Background== | ||
<br> | <br> | ||
| − | ===Magnitude | + | ===Magnitude frequency response and attenuation function=== |
Following relationship exists between the magnitude frequency response and the attenuation function: | Following relationship exists between the magnitude frequency response and the attenuation function: | ||
:$$\left | H_{\rm K}(f)\right |=10^{-a_\text{K}(f)/20} = {\rm e}^{-a_\text{K, Np}(f)}.$$ | :$$\left | H_{\rm K}(f)\right |=10^{-a_\text{K}(f)/20} = {\rm e}^{-a_\text{K, Np}(f)}.$$ | ||
| − | + | #The index "K" makes it clear, that the considered LTI system is a cable $($German: '''K'''abel$)$. | |
| − | + | #For the first calculation rule, the attenuation function $a_\text{K}(f)$ must be used in $\rm dB$ $($"decibel"$)$. | |
| − | + | #For the second calculation rule, the attenuation function $a_\text{K, Np}(f)$ must be used in $\rm Np$ $($"Neper"$)$. | |
| − | + | # The following conversions apply: $\rm 1 \ dB = 0.05 \cdot \ln (10) \ Np= 0.1151 \ Np$ or $\rm 1 \ Np = 20 \cdot \lg (e) \ dB= 8.6859 \ dB$. | |
| − | + | # This applet exclusively uses dB values. | |
| − | ===Attenuation | + | ===Attenuation function of a coaxial cable=== |
| − | According to [Wel77]<ref name ='Wel77'>Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.</ref> the | + | According to [Wel77]<ref name ='Wel77'>Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.</ref> the attenuation function of a coaxial cable of length $l$ is given as follows: |
:$$a_{\rm K}(f)=(\alpha_0+\alpha_1\cdot f+\alpha_2\cdot \sqrt{f}) \cdot l.$$ | :$$a_{\rm K}(f)=(\alpha_0+\alpha_1\cdot f+\alpha_2\cdot \sqrt{f}) \cdot l.$$ | ||
| − | + | #It is important to note the difference between $a_{\rm K}(f)$ in $\rm dB$ and the "alpha" coefficient with other pseudo–units. | |
| − | + | #The attenuation function $a_{\rm K}(f)$ is directly proportional to the cable length $l$. | |
| − | + | # $\alpha_{\rm K}(f)= a_{\rm K}(f)/l$ is referred to as the "attenuation factor" or "kilometric attenuation". | |
| − | + | #The frequency-independent component $α_0$ of the attenuation factor takes into account the Ohmic losses. | |
| − | + | #The frequency-proportional portion $α_1 · f$ of the attenuation factor is due to the derivation losses $($"crosswise loss"$)$. | |
| + | #The dominant portion $α_2$ goes back to the [[Digital_Signal_Transmission/Causes_and_Effects_of_Intersymbol_Interference#Frequency_response_of_a_coaxial_cable|»skin effect«]], which causes a lower current density inside the conductor compared to its surface. | ||
| + | #As a result, the resistance of an electric line increases with the square root of the frequency. | ||
| − | The constants for the ''standard coaxial cable'' with a 2.6 mm inner diameter and a 9.5 mm outer diameter ⇒ short '''Coax (2.6/9.5 mm)''' are: | + | The constants for the »'''standard coaxial cable'''« with a 2.6 mm inner diameter and a 9.5 mm outer diameter ⇒ short '''Coax (2.6/9.5 mm)''' are: |
:$$\alpha_0 = 0.014\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.0038\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 2.36\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$ | :$$\alpha_0 = 0.014\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.0038\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 2.36\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$ | ||
| − | The same applies to the '' | + | The same applies to the »'''small coaxial cable'''« ⇒ short '''Coax (1.2/4.4 mm)''': |
:$$\alpha_0 = 0.068\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} | :$$\alpha_0 = 0.068\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} | ||
\alpha_1 = 0.0039\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 =5.2\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$ | \alpha_1 = 0.0039\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 =5.2\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$ | ||
| + | *These values can be calculated from the cables' geometric dimensions and have been confirmed by measurements at the FTZ in Darmstadt – see [Wel77]<ref name ='Wel77'>Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.</ref>. | ||
| + | *They are valid for a temperature of $\rm 20^\circ \C$ $\rm (293\ K)$ and frequencies greater than $\text{200 kHz}$. | ||
| − | |||
| − | + | ===Attenuation function of a two–wired line=== | |
| − | ===Attenuation | + | According to [PW95]<ref name ='PW95'>Pollakowski, M.; Wellhausen, H.W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Mitteilung aus dem Forschungs- und Technologiezentrum der Deutschen Telekom AG, Darmstadt, Verlag für Wissenschaft und Leben Georg Heidecker, 1995.</ref> the attenuation function of a two–wired line of length $l$ is given as follows: |
| − | According to [PW95]<ref name ='PW95'>Pollakowski, M.; Wellhausen, H.W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Mitteilung aus dem Forschungs- und Technologiezentrum der Deutschen Telekom AG, Darmstadt, Verlag für Wissenschaft und Leben Georg Heidecker, 1995.</ref> the attenuation function of a | ||
:$$a_{\rm K}(f)=(k_1+k_2\cdot (f/{\rm MHz})^{k_3}) \cdot l.$$ | :$$a_{\rm K}(f)=(k_1+k_2\cdot (f/{\rm MHz})^{k_3}) \cdot l.$$ | ||
| − | This function is not directly interpretable, but is a phenomenological description. | + | This function is not directly interpretable, but it is a phenomenological description. |
[PW95]<ref name ='PW95'>Pollakowski, M.; Wellhausen, H.W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Mitteilung aus dem Forschungs- und Technologiezentrum der Deutschen Telekom AG, Darmstadt, Verlag für Wissenschaft und Leben Georg Heidecker, 1995.</ref>also provides the constants determined by measurement results: | [PW95]<ref name ='PW95'>Pollakowski, M.; Wellhausen, H.W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Mitteilung aus dem Forschungs- und Technologiezentrum der Deutschen Telekom AG, Darmstadt, Verlag für Wissenschaft und Leben Georg Heidecker, 1995.</ref>also provides the constants determined by measurement results: | ||
| Line 50: | Line 71: | ||
From these numerical values one recognizes: | From these numerical values one recognizes: | ||
| − | *The attenuation factor $α(f)$ and the attenuation function $a_{\rm K}(f) = α(f) · l$ depend significantly on the pipe diameter. The cables laid since 1994 with $d = 0.35 \ \rm | + | *The attenuation factor $α(f)$ and the attenuation function $a_{\rm K}(f) = α(f) · l$ depend significantly on the pipe diameter. The cables laid since 1994 with $d = 0.35 \ \rm mm$ and $d = 0.5\ \rm mm$ have a $10\%$ greater attenuation factor than the older lines with $d = 0.4\ \rm mm$ or $d= 0.6\ \rm mm$. |
| − | *However, this smaller diameter, which is based on the manufacturing and installation costs, significantly reduces the range $l_{\rm max}$ of the transmission systems used on these lines, so that in the worst case scenario expensive intermediate | + | *However, this smaller diameter, which is based on the manufacturing and installation costs, significantly reduces the range $l_{\rm max}$ of the transmission systems used on these lines, so that in the worst case scenario expensive intermediate regenerators have to be used. |
| − | *The current transmission methods for copper lines prove only a relatively narrow frequency band, for example $120\ \rm kHz$ with [[ | + | *The current transmission methods for copper lines prove only a relatively narrow frequency band, for example $120\ \rm kHz$ with [[Examples_of_Communication_Systems/Allgemeine_Beschreibung_von_ISDN|»ISDN«]] and» $\approx 1100 \ \rm kHz$ with [[Examples_of_Communication_Systems/Allgemeine_Beschreibung_von_DSL|»DSL«]]. For $f = 1 \ \rm MHz$ the attenuation factor of a 0.4 mm cable is around $20 \ \rm dB/km$, so that even with a cable length of $l = 4 \ \rm km$ the attenuation does not exceed $80 \ \rm dB$. |
| − | === | + | ===Conversion between $k$ and $\alpha$ parameters=== |
| − | + | The $k$–parameters of the attenuation factor ⇒ $\alpha_{\rm I} (f)$ can be converted into corresponding $\alpha$–parameters ⇒ $\alpha_{\rm II} (f)$: | |
| − | :$$\alpha_{\rm I} (f) = k_1 + k_2 \cdot (f/f_0)^{k_3}\hspace{0.05cm}, \hspace{0.2cm}{\rm | + | :$$\alpha_{\rm I} (f) = k_1 + k_2 \cdot (f/f_0)^{k_3}\hspace{0.05cm}, \hspace{0.2cm}{\rm with} \hspace{0.15cm} f_0 = 1\,{\rm MHz},$$ |
:$$\alpha_{\rm II} (f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}.$$ | :$$\alpha_{\rm II} (f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}.$$ | ||
| − | + | As a criterion of this conversion, we assume that the quadratic deviation of these two functions is minimal within a bandwidth $B$: | |
:$$\int_{0}^{B} \left [ \alpha_{\rm I} (f) - \alpha_{\rm II} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$ | :$$\int_{0}^{B} \left [ \alpha_{\rm I} (f) - \alpha_{\rm II} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$ | ||
| − | + | It is obvious that $α_0 = k_1$. The parameters $α_1$ and $α_2$ are dependent on the underlying bandwidth $B$ and are: | |
:$$\begin{align*}\alpha_1 & = 15 \cdot (B/f_0)^{k_3 -1}\cdot \frac{k_3 -0.5}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{ {f_0} }\hspace{0.05cm} ,\\ \alpha_2 & = 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{\sqrt{f_0} }\hspace{0.05cm} .\end{align*}$$ | :$$\begin{align*}\alpha_1 & = 15 \cdot (B/f_0)^{k_3 -1}\cdot \frac{k_3 -0.5}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{ {f_0} }\hspace{0.05cm} ,\\ \alpha_2 & = 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{\sqrt{f_0} }\hspace{0.05cm} .\end{align*}$$ | ||
| + | |||
| + | In the opposite direction the conversion rule for the exponent is: | ||
| + | |||
| + | :$$k_3 = \frac{A + 0.5} {A +1}, \hspace{0.2cm}\text{Auxiliary variable: }A = \frac{2} {3} \cdot \frac{\alpha_1 \cdot \sqrt{f_0}}{\alpha_2} \cdot \sqrt{B/f_0}.$$ | ||
| + | |||
| + | With this result you can specify $ k_2 $ with each of the above equations. | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ |
| − | + | #For $k_3 = 1$ $($frequency-proportional attenuation factor$)$ we get $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_1 = {k_2}/{ {f_0} }\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = 0\hspace{0.05cm} .$ | |
| − | + | #For $k_3 = 0.5$ $($skin effect$)$ we get the coefficients: $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm}\alpha_1 = 0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = {k_2}/{\sqrt{f_0} }\hspace{0.05cm}.$ | |
| − | + | #For $k_3 < 0.5$ we get a negative $\alpha_1$ ⇒ conversion is only possible for $0.5 \le k_3 \le 1$. | |
| + | #For $0.5 \le k_3 \le 1$ we get the coefficients $\alpha_1 > 0$ and $\alpha_2 > 0$, which are also dependent on $B/f_0$. | ||
| + | #From $\alpha_1 = 0.3\, {\rm dB}/ ({\rm km \cdot MHz}) \hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 3\, {\rm dB}/ ({\rm km \cdot \sqrt{MHz} })\hspace{0.05cm},\hspace{0.2cm}B = 30 \ \rm MHz$ ⇒ $k_3 = 0.63$, $k_2 = 2.9 \ \rm dB/km$.}} | ||
| + | |||
| + | |||
| + | ===Channel influence on the binary Nyquistent equalization=== | ||
| + | Going by the block diagram: Between the Dirac delta source and the $($threshold$)$ decision are the frequency responses for the | ||
| + | [[File:Applet_Kabeldaempfung_1_version_englisch.png|right|frame|Simplified block diagram of the optimal Nyquist equalizer|class=fit]] | ||
| + | [[File:Applet_Kabeldaempfung_2_version2.png|right|frame|Frequency Response with raised cosine <br> <u>Note:</u> $f_{\rm Nyq} = [f_1 + f_2]/2 =1/(2T)$|class=fit]] | ||
| + | |||
| + | *transmitter $($German: $\rm S$ender$)$ ⇒ $H_{\rm S}(f)$, | ||
| + | *channel $($German: $\rm K$anal$)$ ⇒ $H_{\rm K}(f)$, and | ||
| − | + | *receiver $($German: $\rm E$mpfänger$)$ ⇒ $H_{\rm E}(f)$. | |
| − | |||
| − | + | In this applet | |
| − | + | *we neglect the influence of the transmitted pulse form ⇒ $H_{\rm S}(f) \equiv 1$ ⇒ Dirac delta shaped transmitted signal $s(t)$, and | |
| − | |||
| − | + | *presuppose a binary Nyquist system with raised cosine around the frequency $f_{\rm Nyq}$: | |
| − | * | + | :$$H_{\rm K}(f) · H_{\rm E}(f) = H_{\rm CRO}(f).$$ |
| − | |||
| − | :$$H_{\rm K}(f) · H_{\rm E}(f) = H_{\rm CRO}(f).$$ | ||
| − | + | This means: The [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems#First_Nyquist_criterion_in_the_frequency_domain|»first Nyquist criterion«]] is met<br> ⇒ Timely successive pulses do not disturb each other<br>⇒ there are no [[Digital_Signal_Transmission/Causes_and_Effects_of_Intersymbol_Interference|»intersymbol interferences«]]. | |
| − | + | In the case of white Gaussian noise, the transmission quality is thus determined solely by the noise power in front of the receiver: | |
| − | :$$P_{\rm N} =\frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \ {\rm d}f\hspace{1cm}\text{ | + | :$$P_{\rm N} =\frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \ {\rm d}f\hspace{1cm}\text{with}\hspace{1cm}|H_{\rm E}(f)|^2 = \frac{|H_{\rm CRO}(f)|^2}{|H_{\rm K}(f)|^2}.$$ |
| − | + | The lowest possible noise performance results with | |
| + | #an ideal channel ⇒ $H_{\rm K}(f) \equiv 1$, and | ||
| + | #a rectangular $H_{\rm CRO}(f) \equiv 1$ in $|f| \le f_{\rm Nyq}$: | ||
| − | :$$P_\text{N, min} = P_{\rm N} \ \big [\text{ | + | :$$\Rightarrow \hspace{0.5cm}P_\text{N, min} = P_{\rm N} \ \big [\text{optimal system: }H_{\rm K}(f) \equiv 1, \ r=r_{\rm opt} =1 \big ] = N_0 \cdot f_{\rm Nyq} .$$ |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Definitions:}$ |
| − | * | + | *As a quality criterion for a given system we use the '''total efficiency''' with respect to the channel $\rm (K)$ and the receiver $\rm (E)$: |
| + | |||
| + | :$$\eta_\text{K+E} = \frac{P_{\rm N} \ \big [\text{Optimal system: Channel }H_{\rm K}(f) \equiv 1,\ \text{Roll-off factor } r=r_{\rm opt} =1 \big ]}{P_{\rm N} \ \big [\text{Given system: Channel }H_{\rm K}(f), \ \text{Roll-off factor }r \big ]} =\left [ \frac{1}{3/4 \cdot f_{\rm Nyq} } \cdot \int_{0}^{+\infty} \vert H_{\rm E}(f) \vert^2 \ {\rm d}f \right ]^{-1}\le 1.$$ | ||
| − | :$ | + | This quality criterion is specified in the applet for both parameter sets in logarithm form: $10 \cdot \lg \ \eta_\text{K+E} \le 0 \ \rm dB$. |
| − | + | *Through variation and optimization of the receiver ⇒ roll-off factor $r$ we get the '''channel efficiency''': | |
| − | + | :$$\eta_\text{K} = \min_{0 \le r \le 1} \ \eta_\text{K+E} .$$}} | |
| − | |||
| − | + | [[File:Applet_Kabeldaempfung_3_version2.png|right|frame|Square value frequency response $\left \vert H_{\rm E}(f)\right \vert ^2 $|class=fit]] | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 2:}$ | ||
| + | The graph shows the square value frequency response $\left \vert H_{\rm E}(f)\right \vert ^2 $ with $\left \vert H_{\rm E}(f)\right \vert = H_{\rm CRO}(f) / \left \vert H_{\rm K}(f)\right \vert$ for the following boundary conditions: | ||
| + | *Attenuation function of the channel: $a_{\rm K}(f) = 1 \ {\rm dB} \cdot \sqrt{f/\ {\rm MHz} }$, | ||
| + | *Nyquist frequency: $f_{\rm Nyq} = 20 \ {\rm MHz}$, Roll-off factor $r = 0.5$ | ||
| − | * | + | This results in the following consequences: |
| − | + | *In the area up to $f_{1} = 10 \ \text{MHz: }$ $H_{\rm CRO}(f) = 1$ ⇒ $\left \vert H_{\rm E}(f)\right \vert ^2 = \left \vert H_{\rm K}(f)\right \vert ^{-2}$ (see yellow area). | |
| − | + | * The flank of $H_{\rm CRO}(f)$ is only effective from $f_{1}$ to $f_{2} = 30 \ {\rm MHz}$ and $\left \vert H_{\rm E}(f)\right \vert ^2$ decreases more and more. | |
| − | \ | + | *The maximum of $\left \vert H_{\rm E}(f_{\rm max})\right \vert ^2$ at $f_{\rm max} \approx 11.5 \ {\rm MHz}$ is twice the value of $\left \vert H_{\rm E}(f = 0)\right \vert ^2 = 1$. |
| − | + | *The integral over $\left \vert H_{\rm E}(f)\right \vert ^2$ is a measure of the effective noise power. In the current example this is $4.6$ times bigger than the minimal noise power (for $a_{\rm K}(f) = 0 \ {\rm dB}$ and $r=1$) ⇒ $10 \cdot \lg \ \eta_\text{K+E} \approx - 6.6 \ {\rm dB}.$}} | |
| − | |||
| − | + | ==Exercises== | |
| − | |||
| − | |||
| − | :$$ | + | [[File:Applet_Kabeldaempfung_6_version1.png|right]] |
| − | + | *First choose an exercise number $1$ ... $11$. | |
| − | + | *An exercise description is displayed. | |
| + | *Parameter values are adjusted to the respective exercises. | ||
| + | *Click "Show solution" to display the solution. | ||
| + | *Exercise description and solution are in English. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Number "0" is a "Reset" button: | |
| + | *Sets parameters to initial values (like after loading the section). | ||
| + | *Displays a "Reset text" to further describe the applet. | ||
| + | |||
| + | |||
| + | In the following desctiption '''Blue''' means the left parameter set (blue in the applet), and '''Red''' means the right parameter set (red in the applet). For parameters that are marked with an apostrophe the unit is not displayed. For example we write ${\alpha_2}' =2$ for $\alpha_2 =2\, {\rm dB} / ({\rm km \cdot \sqrt{MHz} })$. | ||
| + | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | '''(1)''' First set '''Blue''' to $\text{Coax (1.2/4.4 mm)}$ and then to $\text{Coax (2.6/9.5 mm)}$. The cable length is $l_{\rm Blue}= 5\ \rm km$. |
| − | + | :Interpret $a_{\rm K}(f)$ and $\vert H_{\rm K}(f) \vert$, in particular the functional values $a_{\rm K}(f = f_\star = 30 \ \rm MHz)$ and $\vert H_{\rm K}(f = 0) \vert$.}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | $\Rightarrow\hspace{0.3cm}\text{The attenuation function increases approximately with }\sqrt{f}\text{ and the magnitude frequency response decreases similarly to an exponential function};$ | ||
| + | $\hspace{1.15cm}\text{Coax (1.2/4.4 mm): }a_{\rm K}(f = f_\star) = 143.3\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.96.$ | ||
| − | $ | + | $\hspace{1.15cm}\text{Coax (2.6/9.5 mm): }a_{\rm K}(f = f_\star) = 65.3\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.99;$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {{ | + | {{BlaueBox|TEXT= |
| + | '''(2)''' Set '''Blue''' to $\text{Coax (2.6/9.5 mm)}$ and $l_{\rm Blue} = 5\ \rm km$. How is $a_{\rm K}(f =f_\star = 30 \ \rm MHz)$ affected by $\alpha_0$, $\alpha_1$ und $\alpha_2$?}} | ||
| − | |||
| − | |||
| − | {{ | + | $\Rightarrow\hspace{0.3cm}\alpha_2\text{ is dominant due to the skin effect. The contributions of } \alpha_0\text{ (ca. 0.1 dB) and }\alpha_1 \text{ (ca. 0.6 dB) are comparatively small.}$ |
| − | == | + | {{BlaueBox|TEXT= |
| + | '''(3)''' Additionally, set '''Red''' to $\text{Two–wired Line (0.5 mm)}$ and $l_{\rm Red} = 1\ \rm km$. What is the resulting value for $a_{\rm K}(f =f_\star= 30 \ \rm MHz)$? | ||
| + | :Up to what length $l_{\rm Red}$ does the red attenuation function stay under the blue one?}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Red curve: }a_{\rm K}(f = f_\star) = 87.5 {\ \rm dB} \text{. The condition above is fulfilled for }l_{\rm Red} = 0.7\ {\rm km} \ \Rightarrow \ a_{\rm K}(f = f_\star) = 61.3 {\ \rm dB}.$ | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | '''(4)''' Set '''Red''' to ${k_1}' = 0, {k_2}' = 10, {k_3}' = 0.75, {l_{\rm red} } = 1 \ \rm km$ and vary the Parameter $0.5 \le k_3 \le 1$. | |
| − | + | :How do the parameters affect $a_{\rm K}(f)$ and $\vert H_{\rm K}(f) \vert$? }} | |
| − | + | $\Rightarrow\hspace{0.3cm}\text{With }k_2\text {being constant, }a_{\rm K}(f)\text{ increases with bigger values of }k_3\text{ and }\vert H_{\rm K}(f) \vert \text{ decreases faster and faster. With }k_3 =1: a_{\rm K}(f)\text{ rises linearly.}$ | |
| − | |||
| − | |||
| + | $\hspace{1.15cm}\text{With }k_3 \to 0.5, \text{ the attenuation function is more and more determined by the skin effect, same as in the coaxial cable.}$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(5)''' Set '''Red''' to $\text{Two–wired Line (0.5 mm)}$ and '''Blue''' to $\text{Conversion of Red}$. For the length use $l_{\rm Red} = l_{\rm Blue} = 1\ \rm km$. |
| − | : | + | :Analyse and interpret the displayed functions $a_{\rm K}(f)$ and $\vert H_{\rm K}(f) \vert$.}} |
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Very good approximation of the two-wire line through the blue parameter set, both with regard to }a_{\rm K}(f) \text{, as well as }\vert H_{\rm K}(f) \vert.$ | ||
| + | $\hspace{1.15cm}\text{The resulting parameters from the conversion are }{\alpha_0}' = {k_1}' = 4.4, \ {\alpha_1}' = 0.76, \ {\alpha_2}' = 11.12.$ | ||
| − | + | {{BlaueBox|TEXT= | |
| + | '''(6)''' We assume the settings of '''(5)'''. Which parts of the attenuation function are due to ohmic loss, lateral losses and skin effect? }} | ||
| − | |||
| − | $\hspace{ | + | $\Rightarrow\hspace{0.3cm}\text{Solution based on '''Blue''': }a_{\rm K}(f = f_\star= 30 \ {\rm MHz}) = 88.1\ {\rm dB}, \hspace{0.2cm}\text{without }\alpha_0\text{: }83.7\ {\rm dB}, \hspace{0.2cm}\text{without }\alpha_0 \text{ and } \alpha_1\text{: }60.9\ {\rm dB}.$ |
| + | $\hspace{1.15cm}\text{For a two-wire cable, the influence of the longitudinal and transverse losses is significantly greater than for a coaxial cable.}$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(7)''' Set '''Blue''' to ${\alpha_0}' = {\alpha_1}' ={\alpha_2}' = 0$ and '''Red''' to ${k_1}' = 2, {k_2}' = 0, {l_{\rm red} } = 1 \ \rm km$. Additionally, set ${f_{\rm Nyq} }' =15$ and $r= 0.5$. |
| + | :How big are the total efficiency $\eta_\text{K+E}$ and the channel efficiency $\eta_\text{K}$?}} | ||
| − | $\Rightarrow\hspace{0.3cm}\text{ | + | $\Rightarrow\hspace{0.3cm}10 \cdot \lg \ \eta_\text{K+E} = -0.7\ \ {\rm dB}\text{ (Blue: ideal system) and }10 \cdot \lg \ \eta_\text{K+E} = -2.7\ \ {\rm dB}\text{ (Red: DC signal attenuation only)}$. |
| + | |||
| + | $\hspace{0.95cm}\text{The best possible rolloff factor is }r = 1.\text{ Therefore }10 \cdot \lg \ \eta_\text{K} = 0 \ {\rm dB}\text{ (Blue) or }10 \cdot \lg \ \eta_\text{K} = -2\ {\rm dB}\text{ (Red)}.$ | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(8)''' The same settings apply as in '''(7)'''. Under what transmission power $P_{\rm red}$ with respect to $P_{\rm blue}$ do both systems achieve the same error probability? }} | ||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{We need to achieve }10 \cdot \lg {P_{\rm Red}}/{P_{\rm Blue}} = 2 \ {\rm dB} \ \ \Rightarrow \ \ {P_{\rm Red}}/{P_{\rm Blue}} = 10^{0.2} = 1.585.$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(9)''' Set '''Blue''' to ${\alpha_0}' = {\alpha_1}' = 0, \ {\alpha_2}' = 3, \ {l_{\rm blue} }' = 2$ and '''Red''' to "Inactive". Additionally set ${f_{\rm Nyq} }' =15$ and $r= 0.7$. |
| − | + | :How does $\vert H_{\rm E}(f) \vert$ look like? Calculate the total efficiency $\eta_\text{K+E}$ and the channel efficiency$\eta_\text{K}$.}} | |
| − | $\Rightarrow\hspace{0.3cm}\text{ | + | $\Rightarrow\hspace{0.3cm}\text{For} f < 7.5 {\ \rm MHz: } \vert H_{\rm E}(f) \vert = \vert H_{\rm K}(f) \vert ^{-1}.\text{ For } f > 25 {\ \rm MHz: }\vert H_{\rm E}(f) \vert = 0.\text{ In between, the effect of the CRO edge can be observed.}$ |
| + | $\hspace{0.95cm}\text{The best possible rolloff factor }r = 0.7 \text{ is already set }\Rightarrow \ 10 \cdot \lg \ \eta_\text{K+E} = 10 \cdot \lg \ \eta_\text{K} \approx - 18.1 \ {\rm dB}.$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(10)''' Set '''Blue''' to ${\alpha_0}' = {\alpha_1}' = 0, \ {\alpha_2}' = 3, \ {l_{\rm blue} }' = 8$ and '''Red''' to "Inactive". Additionally, set ${f_{\rm Nyq} }' =15$ and $r= 0.7$. |
| − | : | + | :How big is $\vert H_{\rm E}(f = 0) \vert$? What is the maximum value of $\vert H_{\rm E}(f) \vert$? Calculate the channel efficiency $\eta_\text{K}$.}} |
| − | $\Rightarrow\hspace{0.3cm}\ | + | $\Rightarrow\hspace{0.3cm}\vert H_{\rm E}(f = 0) \vert = \vert H_{\rm E}(f = 0) \vert ^{-1}= 1 \text{ and the maximum value } \vert H_{\rm E}(f) \vert \text{ is approximately }37500\text{ for }r=0.7 \Rightarrow 10 \cdot \lg \ \eta_\text{K+E} \approx -89.2 \ {\rm dB},$ |
| + | $\hspace{0.95cm}\text{because the integral over }\vert H_{\rm E}(f) \vert^2\text{is huge. After the optimization }r=0.17 \text{ we get }10 \cdot \lg \ \eta_\text{K} \approx -82.6 \ {\rm dB}.$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(11)''' The same settings apply as in '''(10)''' and $r= 0.17$. Vary the cable length up to $l_{\rm blue} = 10 \ \rm km$. |
| + | :How much do the maximum value of $\vert H_{\rm E}(f) \vert$, the channel efficiency $\eta_\text{K}$ and the optimal rolloff factor $r_{\rm opt}$ change?}} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{The maximum value of } \vert H_{\rm E}(f) \vert \text{ increases and }10 \cdot \lg \ \eta_\text{K} \text{ decreases more and more.}$ | ||
| + | |||
| + | $\hspace{0.95cm}\text{At 10 km length } 10 \cdot \lg \ \eta_\text{K} \approx -104.9 \ {\rm dB} \text{ and } r_{\rm opt}=0.14\text{. For }f_\star \approx 14.5\ {\rm MHz} \Rightarrow \vert H_{\rm E}(f = f_\star) \vert = 352000 \approx \vert H_{\rm E}(f =0)\vert$. | ||
| + | |||
| + | ==Applet Manual== | ||
| + | [[File:Applet_Kabeldaempfung_5_version2.png|left|600px]] | ||
| + | '''(A)''' Preselection for blue parameter set | ||
| + | |||
| + | '''(B)''' Input of the $\alpha$ parameters via sliders | ||
| + | |||
| + | '''(C)''' Preselection for red parameter set | ||
| + | '''(D)''' Input of the $k$ parameters via sliders | ||
| − | + | '''(E)''' Input of the parameters $f_{\rm Nyq}$ and $r$ | |
| − | + | '''(F)''' Selection for the graphic display | |
| + | '''(G)''' Display $a_\text{K}(f)$, $|H_\text{K}(f)|$, $|H_\text{E}(f)|$, ... | ||
| − | + | '''(H)''' Scaling factor $H_0$ for $|H_\text{E}(f)|$, $|H_\text{E}(f)|^2$ | |
| − | '''( | + | |
| + | '''(I)''' Selection of the frequency $f_\star$ for numeric values | ||
| + | |||
| + | '''(J)''' Numeric values for blue parameter set | ||
| + | |||
| + | '''(K)''' Numeric values for red parameter set | ||
| + | '''(L)''' Output system efficiency $\eta_\text{K+E}$ in dB | ||
| − | + | '''(M)''' Store & Recall of settings | |
| − | + | '''(N)''' Exercise section | |
| + | '''(O)''' Variation of the graphic display:$\hspace{0.5cm}$"$+$" (Zoom in), | ||
| + | $\hspace{0.5cm}$ "$-$" (Zoom out) | ||
| + | $\hspace{0.5cm}$ "$\rm o$" (Reset) | ||
| + | $\hspace{0.5cm}$ "$\leftarrow$" (Move left), etc. | ||
| + | '''Other options for graphic display''': | ||
| + | *Hold shift and scroll: Zoom in on/out of coordinate system, | ||
| + | *Hold shift and left click: Move the coordinate system. | ||
| − | == | + | ==About the Authors== |
| + | This interactive calculation was designed and realized at the [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] of the [https://www.tum.de/ Technische Universität München]. | ||
| + | *The original version was created in 2009 by [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Sebastian_Seitz_.28Diplomarbeit_LB_2009.29|Sebastian Seitz]] as part of his Diploma thesis using "FlashMX–Actionscript" (Supervisor: [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]] ). | ||
| + | *In 2018 this Applet was redesigned and updated to "HTML5" by [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Jimmy_He_.28Bachelorarbeit_2018.29|Jimmy He]] as part of his Bachelor's thesis (Supervisor: [[Biographies_and_Bibliographies/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]]) . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Once again: Open Applet in new Tab== |
| − | {{ | + | {{LntAppletLinkEn|attenuationCopperCables_en}} |
Latest revision as of 15:25, 8 April 2023
Open Applet in new Tab English Applet with German WIKI description
Contents
Applet Description
This applet calculates the attenuation function $a_{\rm K}(f)$ of conducted transmission media $($with cable length $l)$:
- For coaxial cables one usually uses the equation $a_{\rm K}(f)=(\alpha_0+\alpha_1\cdot f+\alpha_2\cdot \sqrt{f}) \cdot l$.
- In contrast, two-wire lines are often displayed in the form $a_{\rm K}(f)=(k_1+k_2\cdot (f/{\rm MHz})^{k_3}) \cdot l$.
- The conversion of the $(k_1, \ k_2, \ k_3)$ parameters to the $(\alpha_0, \ \alpha_1, \ \alpha_2)$ parameters for $B = 30 \ \rm MHz$ is realized as well as the other way around.
Aside from the attenuation function $a_{\rm K}(f)$ the applet can display:
- the associated magnitude frequency response $\left | H_{\rm K}(f)\right |=10^{-a_\text{K}(f)/20},$
- the equalizer frequency response $\left | H_{\rm E}(f)\right | = \left | H_{\rm CRO}(f) / H_{\rm K}(f)\right | $, that leads to a Nyquist total frequency response $ H_{\rm CRO}(f) $,
- the corresponding squared magnitude frequency response $\left | H_{\rm E}(f)\right |^2 $.
The integral over $\left | H_{\rm E}(f)\right |^2 $ is a measure of the noise exaggeration of the selected Nyquist total frequency response and thus also for the expected error probability. From this, the »total efficiency« $\eta_\text{K+E}$ for the channel $($German: Kanal$)$ plus the equalizer $($German: Entzerrer$)$ is calculated, which in the applet is output in $\rm dB$.
Through optimization of the roll-off factor $r$ of the raised cosine frequency response $ H_{\rm CRO}(f) $ one gets the »channel efficiency« $ \eta_\text{K}$. This value indicates the deterioration of the overall system due to the attenuation function $ a_{\rm K} (f) $ of the transmission medium.
Theoretical Background
Magnitude frequency response and attenuation function
Following relationship exists between the magnitude frequency response and the attenuation function:
- $$\left | H_{\rm K}(f)\right |=10^{-a_\text{K}(f)/20} = {\rm e}^{-a_\text{K, Np}(f)}.$$
- The index "K" makes it clear, that the considered LTI system is a cable $($German: Kabel$)$.
- For the first calculation rule, the attenuation function $a_\text{K}(f)$ must be used in $\rm dB$ $($"decibel"$)$.
- For the second calculation rule, the attenuation function $a_\text{K, Np}(f)$ must be used in $\rm Np$ $($"Neper"$)$.
- The following conversions apply: $\rm 1 \ dB = 0.05 \cdot \ln (10) \ Np= 0.1151 \ Np$ or $\rm 1 \ Np = 20 \cdot \lg (e) \ dB= 8.6859 \ dB$.
- This applet exclusively uses dB values.
Attenuation function of a coaxial cable
According to [Wel77][1] the attenuation function of a coaxial cable of length $l$ is given as follows:
- $$a_{\rm K}(f)=(\alpha_0+\alpha_1\cdot f+\alpha_2\cdot \sqrt{f}) \cdot l.$$
- It is important to note the difference between $a_{\rm K}(f)$ in $\rm dB$ and the "alpha" coefficient with other pseudo–units.
- The attenuation function $a_{\rm K}(f)$ is directly proportional to the cable length $l$.
- $\alpha_{\rm K}(f)= a_{\rm K}(f)/l$ is referred to as the "attenuation factor" or "kilometric attenuation".
- The frequency-independent component $α_0$ of the attenuation factor takes into account the Ohmic losses.
- The frequency-proportional portion $α_1 · f$ of the attenuation factor is due to the derivation losses $($"crosswise loss"$)$.
- The dominant portion $α_2$ goes back to the »skin effect«, which causes a lower current density inside the conductor compared to its surface.
- As a result, the resistance of an electric line increases with the square root of the frequency.
The constants for the »standard coaxial cable« with a 2.6 mm inner diameter and a 9.5 mm outer diameter ⇒ short Coax (2.6/9.5 mm) are:
- $$\alpha_0 = 0.014\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.0038\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 2.36\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$
The same applies to the »small coaxial cable« ⇒ short Coax (1.2/4.4 mm):
- $$\alpha_0 = 0.068\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.0039\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 =5.2\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$
- These values can be calculated from the cables' geometric dimensions and have been confirmed by measurements at the FTZ in Darmstadt – see [Wel77][1].
- They are valid for a temperature of $\rm 20^\circ \C$ $\rm (293\ K)$ and frequencies greater than $\text{200 kHz}$.
Attenuation function of a two–wired line
According to [PW95][2] the attenuation function of a two–wired line of length $l$ is given as follows:
- $$a_{\rm K}(f)=(k_1+k_2\cdot (f/{\rm MHz})^{k_3}) \cdot l.$$
This function is not directly interpretable, but it is a phenomenological description.
[PW95][2]also provides the constants determined by measurement results:
- $d = 0.35 \ {\rm mm}$: $k_1 = 7.9 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 15.1 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.62$,
- $d = 0.40 \ {\rm mm}$: $k_1 = 5.1 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 14.3 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.59$,
- $d = 0.50 \ {\rm mm}$: $k_1 = 4.4 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 10.8 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.60$,
- $d = 0.60 \ {\rm mm}$: $k_1 = 3.8 \ {\rm dB/km}, \hspace{0.2cm}k_2 = \hspace{0.25cm}9.2 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.61$.
From these numerical values one recognizes:
- The attenuation factor $α(f)$ and the attenuation function $a_{\rm K}(f) = α(f) · l$ depend significantly on the pipe diameter. The cables laid since 1994 with $d = 0.35 \ \rm mm$ and $d = 0.5\ \rm mm$ have a $10\%$ greater attenuation factor than the older lines with $d = 0.4\ \rm mm$ or $d= 0.6\ \rm mm$.
- However, this smaller diameter, which is based on the manufacturing and installation costs, significantly reduces the range $l_{\rm max}$ of the transmission systems used on these lines, so that in the worst case scenario expensive intermediate regenerators have to be used.
- The current transmission methods for copper lines prove only a relatively narrow frequency band, for example $120\ \rm kHz$ with »ISDN« and» $\approx 1100 \ \rm kHz$ with »DSL«. For $f = 1 \ \rm MHz$ the attenuation factor of a 0.4 mm cable is around $20 \ \rm dB/km$, so that even with a cable length of $l = 4 \ \rm km$ the attenuation does not exceed $80 \ \rm dB$.
Conversion between $k$ and $\alpha$ parameters
The $k$–parameters of the attenuation factor ⇒ $\alpha_{\rm I} (f)$ can be converted into corresponding $\alpha$–parameters ⇒ $\alpha_{\rm II} (f)$:
- $$\alpha_{\rm I} (f) = k_1 + k_2 \cdot (f/f_0)^{k_3}\hspace{0.05cm}, \hspace{0.2cm}{\rm with} \hspace{0.15cm} f_0 = 1\,{\rm MHz},$$
- $$\alpha_{\rm II} (f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}.$$
As a criterion of this conversion, we assume that the quadratic deviation of these two functions is minimal within a bandwidth $B$:
- $$\int_{0}^{B} \left [ \alpha_{\rm I} (f) - \alpha_{\rm II} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$
It is obvious that $α_0 = k_1$. The parameters $α_1$ and $α_2$ are dependent on the underlying bandwidth $B$ and are:
- $$\begin{align*}\alpha_1 & = 15 \cdot (B/f_0)^{k_3 -1}\cdot \frac{k_3 -0.5}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{ {f_0} }\hspace{0.05cm} ,\\ \alpha_2 & = 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{\sqrt{f_0} }\hspace{0.05cm} .\end{align*}$$
In the opposite direction the conversion rule for the exponent is:
- $$k_3 = \frac{A + 0.5} {A +1}, \hspace{0.2cm}\text{Auxiliary variable: }A = \frac{2} {3} \cdot \frac{\alpha_1 \cdot \sqrt{f_0}}{\alpha_2} \cdot \sqrt{B/f_0}.$$
With this result you can specify $ k_2 $ with each of the above equations.
$\text{Example 1:}$
- For $k_3 = 1$ $($frequency-proportional attenuation factor$)$ we get $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_1 = {k_2}/{ {f_0} }\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = 0\hspace{0.05cm} .$
- For $k_3 = 0.5$ $($skin effect$)$ we get the coefficients: $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm}\alpha_1 = 0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = {k_2}/{\sqrt{f_0} }\hspace{0.05cm}.$
- For $k_3 < 0.5$ we get a negative $\alpha_1$ ⇒ conversion is only possible for $0.5 \le k_3 \le 1$.
- For $0.5 \le k_3 \le 1$ we get the coefficients $\alpha_1 > 0$ and $\alpha_2 > 0$, which are also dependent on $B/f_0$.
- From $\alpha_1 = 0.3\, {\rm dB}/ ({\rm km \cdot MHz}) \hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 3\, {\rm dB}/ ({\rm km \cdot \sqrt{MHz} })\hspace{0.05cm},\hspace{0.2cm}B = 30 \ \rm MHz$ ⇒ $k_3 = 0.63$, $k_2 = 2.9 \ \rm dB/km$.
Channel influence on the binary Nyquistent equalization
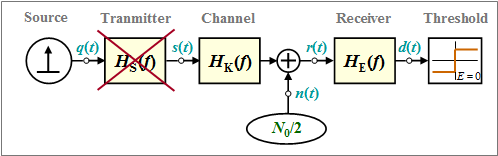
Going by the block diagram: Between the Dirac delta source and the $($threshold$)$ decision are the frequency responses for the
- transmitter $($German: $\rm S$ender$)$ ⇒ $H_{\rm S}(f)$,
- channel $($German: $\rm K$anal$)$ ⇒ $H_{\rm K}(f)$, and
- receiver $($German: $\rm E$mpfänger$)$ ⇒ $H_{\rm E}(f)$.
In this applet
- we neglect the influence of the transmitted pulse form ⇒ $H_{\rm S}(f) \equiv 1$ ⇒ Dirac delta shaped transmitted signal $s(t)$, and
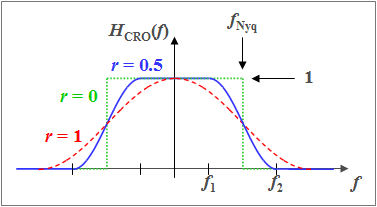
- presuppose a binary Nyquist system with raised cosine around the frequency $f_{\rm Nyq}$:
- $$H_{\rm K}(f) · H_{\rm E}(f) = H_{\rm CRO}(f).$$
This means: The »first Nyquist criterion« is met
⇒ Timely successive pulses do not disturb each other
⇒ there are no »intersymbol interferences«.
In the case of white Gaussian noise, the transmission quality is thus determined solely by the noise power in front of the receiver:
- $$P_{\rm N} =\frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \ {\rm d}f\hspace{1cm}\text{with}\hspace{1cm}|H_{\rm E}(f)|^2 = \frac{|H_{\rm CRO}(f)|^2}{|H_{\rm K}(f)|^2}.$$
The lowest possible noise performance results with
- an ideal channel ⇒ $H_{\rm K}(f) \equiv 1$, and
- a rectangular $H_{\rm CRO}(f) \equiv 1$ in $|f| \le f_{\rm Nyq}$:
- $$\Rightarrow \hspace{0.5cm}P_\text{N, min} = P_{\rm N} \ \big [\text{optimal system: }H_{\rm K}(f) \equiv 1, \ r=r_{\rm opt} =1 \big ] = N_0 \cdot f_{\rm Nyq} .$$
$\text{Definitions:}$
- As a quality criterion for a given system we use the total efficiency with respect to the channel $\rm (K)$ and the receiver $\rm (E)$:
- $$\eta_\text{K+E} = \frac{P_{\rm N} \ \big [\text{Optimal system: Channel }H_{\rm K}(f) \equiv 1,\ \text{Roll-off factor } r=r_{\rm opt} =1 \big ]}{P_{\rm N} \ \big [\text{Given system: Channel }H_{\rm K}(f), \ \text{Roll-off factor }r \big ]} =\left [ \frac{1}{3/4 \cdot f_{\rm Nyq} } \cdot \int_{0}^{+\infty} \vert H_{\rm E}(f) \vert^2 \ {\rm d}f \right ]^{-1}\le 1.$$
This quality criterion is specified in the applet for both parameter sets in logarithm form: $10 \cdot \lg \ \eta_\text{K+E} \le 0 \ \rm dB$.
- Through variation and optimization of the receiver ⇒ roll-off factor $r$ we get the channel efficiency:
- $$\eta_\text{K} = \min_{0 \le r \le 1} \ \eta_\text{K+E} .$$
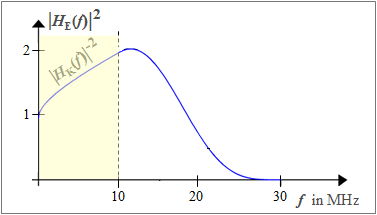
$\text{Example 2:}$ The graph shows the square value frequency response $\left \vert H_{\rm E}(f)\right \vert ^2 $ with $\left \vert H_{\rm E}(f)\right \vert = H_{\rm CRO}(f) / \left \vert H_{\rm K}(f)\right \vert$ for the following boundary conditions:
- Attenuation function of the channel: $a_{\rm K}(f) = 1 \ {\rm dB} \cdot \sqrt{f/\ {\rm MHz} }$,
- Nyquist frequency: $f_{\rm Nyq} = 20 \ {\rm MHz}$, Roll-off factor $r = 0.5$
This results in the following consequences:
- In the area up to $f_{1} = 10 \ \text{MHz: }$ $H_{\rm CRO}(f) = 1$ ⇒ $\left \vert H_{\rm E}(f)\right \vert ^2 = \left \vert H_{\rm K}(f)\right \vert ^{-2}$ (see yellow area).
- The flank of $H_{\rm CRO}(f)$ is only effective from $f_{1}$ to $f_{2} = 30 \ {\rm MHz}$ and $\left \vert H_{\rm E}(f)\right \vert ^2$ decreases more and more.
- The maximum of $\left \vert H_{\rm E}(f_{\rm max})\right \vert ^2$ at $f_{\rm max} \approx 11.5 \ {\rm MHz}$ is twice the value of $\left \vert H_{\rm E}(f = 0)\right \vert ^2 = 1$.
- The integral over $\left \vert H_{\rm E}(f)\right \vert ^2$ is a measure of the effective noise power. In the current example this is $4.6$ times bigger than the minimal noise power (for $a_{\rm K}(f) = 0 \ {\rm dB}$ and $r=1$) ⇒ $10 \cdot \lg \ \eta_\text{K+E} \approx - 6.6 \ {\rm dB}.$
Exercises
- First choose an exercise number $1$ ... $11$.
- An exercise description is displayed.
- Parameter values are adjusted to the respective exercises.
- Click "Show solution" to display the solution.
- Exercise description and solution are in English.
Number "0" is a "Reset" button:
- Sets parameters to initial values (like after loading the section).
- Displays a "Reset text" to further describe the applet.
In the following desctiption Blue means the left parameter set (blue in the applet), and Red means the right parameter set (red in the applet). For parameters that are marked with an apostrophe the unit is not displayed. For example we write ${\alpha_2}' =2$ for $\alpha_2 =2\, {\rm dB} / ({\rm km \cdot \sqrt{MHz} })$.
(1) First set Blue to $\text{Coax (1.2/4.4 mm)}$ and then to $\text{Coax (2.6/9.5 mm)}$. The cable length is $l_{\rm Blue}= 5\ \rm km$.
- Interpret $a_{\rm K}(f)$ and $\vert H_{\rm K}(f) \vert$, in particular the functional values $a_{\rm K}(f = f_\star = 30 \ \rm MHz)$ and $\vert H_{\rm K}(f = 0) \vert$.
$\Rightarrow\hspace{0.3cm}\text{The attenuation function increases approximately with }\sqrt{f}\text{ and the magnitude frequency response decreases similarly to an exponential function};$
$\hspace{1.15cm}\text{Coax (1.2/4.4 mm): }a_{\rm K}(f = f_\star) = 143.3\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.96.$
$\hspace{1.15cm}\text{Coax (2.6/9.5 mm): }a_{\rm K}(f = f_\star) = 65.3\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.99;$
(2) Set Blue to $\text{Coax (2.6/9.5 mm)}$ and $l_{\rm Blue} = 5\ \rm km$. How is $a_{\rm K}(f =f_\star = 30 \ \rm MHz)$ affected by $\alpha_0$, $\alpha_1$ und $\alpha_2$?
$\Rightarrow\hspace{0.3cm}\alpha_2\text{ is dominant due to the skin effect. The contributions of } \alpha_0\text{ (ca. 0.1 dB) and }\alpha_1 \text{ (ca. 0.6 dB) are comparatively small.}$
(3) Additionally, set Red to $\text{Two–wired Line (0.5 mm)}$ and $l_{\rm Red} = 1\ \rm km$. What is the resulting value for $a_{\rm K}(f =f_\star= 30 \ \rm MHz)$?
- Up to what length $l_{\rm Red}$ does the red attenuation function stay under the blue one?
$\Rightarrow\hspace{0.3cm}\text{Red curve: }a_{\rm K}(f = f_\star) = 87.5 {\ \rm dB} \text{. The condition above is fulfilled for }l_{\rm Red} = 0.7\ {\rm km} \ \Rightarrow \ a_{\rm K}(f = f_\star) = 61.3 {\ \rm dB}.$
(4) Set Red to ${k_1}' = 0, {k_2}' = 10, {k_3}' = 0.75, {l_{\rm red} } = 1 \ \rm km$ and vary the Parameter $0.5 \le k_3 \le 1$.
- How do the parameters affect $a_{\rm K}(f)$ and $\vert H_{\rm K}(f) \vert$?
$\Rightarrow\hspace{0.3cm}\text{With }k_2\text {being constant, }a_{\rm K}(f)\text{ increases with bigger values of }k_3\text{ and }\vert H_{\rm K}(f) \vert \text{ decreases faster and faster. With }k_3 =1: a_{\rm K}(f)\text{ rises linearly.}$
$\hspace{1.15cm}\text{With }k_3 \to 0.5, \text{ the attenuation function is more and more determined by the skin effect, same as in the coaxial cable.}$
(5) Set Red to $\text{Two–wired Line (0.5 mm)}$ and Blue to $\text{Conversion of Red}$. For the length use $l_{\rm Red} = l_{\rm Blue} = 1\ \rm km$.
- Analyse and interpret the displayed functions $a_{\rm K}(f)$ and $\vert H_{\rm K}(f) \vert$.
$\Rightarrow\hspace{0.3cm}\text{Very good approximation of the two-wire line through the blue parameter set, both with regard to }a_{\rm K}(f) \text{, as well as }\vert H_{\rm K}(f) \vert.$
$\hspace{1.15cm}\text{The resulting parameters from the conversion are }{\alpha_0}' = {k_1}' = 4.4, \ {\alpha_1}' = 0.76, \ {\alpha_2}' = 11.12.$
(6) We assume the settings of (5). Which parts of the attenuation function are due to ohmic loss, lateral losses and skin effect?
$\Rightarrow\hspace{0.3cm}\text{Solution based on '''Blue''': }a_{\rm K}(f = f_\star= 30 \ {\rm MHz}) = 88.1\ {\rm dB}, \hspace{0.2cm}\text{without }\alpha_0\text{: }83.7\ {\rm dB}, \hspace{0.2cm}\text{without }\alpha_0 \text{ and } \alpha_1\text{: }60.9\ {\rm dB}.$
$\hspace{1.15cm}\text{For a two-wire cable, the influence of the longitudinal and transverse losses is significantly greater than for a coaxial cable.}$
(7) Set Blue to ${\alpha_0}' = {\alpha_1}' ={\alpha_2}' = 0$ and Red to ${k_1}' = 2, {k_2}' = 0, {l_{\rm red} } = 1 \ \rm km$. Additionally, set ${f_{\rm Nyq} }' =15$ and $r= 0.5$.
- How big are the total efficiency $\eta_\text{K+E}$ and the channel efficiency $\eta_\text{K}$?
$\Rightarrow\hspace{0.3cm}10 \cdot \lg \ \eta_\text{K+E} = -0.7\ \ {\rm dB}\text{ (Blue: ideal system) and }10 \cdot \lg \ \eta_\text{K+E} = -2.7\ \ {\rm dB}\text{ (Red: DC signal attenuation only)}$.
$\hspace{0.95cm}\text{The best possible rolloff factor is }r = 1.\text{ Therefore }10 \cdot \lg \ \eta_\text{K} = 0 \ {\rm dB}\text{ (Blue) or }10 \cdot \lg \ \eta_\text{K} = -2\ {\rm dB}\text{ (Red)}.$
(8) The same settings apply as in (7). Under what transmission power $P_{\rm red}$ with respect to $P_{\rm blue}$ do both systems achieve the same error probability?
$\Rightarrow\hspace{0.3cm}\text{We need to achieve }10 \cdot \lg {P_{\rm Red}}/{P_{\rm Blue}} = 2 \ {\rm dB} \ \ \Rightarrow \ \ {P_{\rm Red}}/{P_{\rm Blue}} = 10^{0.2} = 1.585.$
(9) Set Blue to ${\alpha_0}' = {\alpha_1}' = 0, \ {\alpha_2}' = 3, \ {l_{\rm blue} }' = 2$ and Red to "Inactive". Additionally set ${f_{\rm Nyq} }' =15$ and $r= 0.7$.
- How does $\vert H_{\rm E}(f) \vert$ look like? Calculate the total efficiency $\eta_\text{K+E}$ and the channel efficiency$\eta_\text{K}$.
$\Rightarrow\hspace{0.3cm}\text{For} f < 7.5 {\ \rm MHz: } \vert H_{\rm E}(f) \vert = \vert H_{\rm K}(f) \vert ^{-1}.\text{ For } f > 25 {\ \rm MHz: }\vert H_{\rm E}(f) \vert = 0.\text{ In between, the effect of the CRO edge can be observed.}$
$\hspace{0.95cm}\text{The best possible rolloff factor }r = 0.7 \text{ is already set }\Rightarrow \ 10 \cdot \lg \ \eta_\text{K+E} = 10 \cdot \lg \ \eta_\text{K} \approx - 18.1 \ {\rm dB}.$
(10) Set Blue to ${\alpha_0}' = {\alpha_1}' = 0, \ {\alpha_2}' = 3, \ {l_{\rm blue} }' = 8$ and Red to "Inactive". Additionally, set ${f_{\rm Nyq} }' =15$ and $r= 0.7$.
- How big is $\vert H_{\rm E}(f = 0) \vert$? What is the maximum value of $\vert H_{\rm E}(f) \vert$? Calculate the channel efficiency $\eta_\text{K}$.
$\Rightarrow\hspace{0.3cm}\vert H_{\rm E}(f = 0) \vert = \vert H_{\rm E}(f = 0) \vert ^{-1}= 1 \text{ and the maximum value } \vert H_{\rm E}(f) \vert \text{ is approximately }37500\text{ for }r=0.7 \Rightarrow 10 \cdot \lg \ \eta_\text{K+E} \approx -89.2 \ {\rm dB},$
$\hspace{0.95cm}\text{because the integral over }\vert H_{\rm E}(f) \vert^2\text{is huge. After the optimization }r=0.17 \text{ we get }10 \cdot \lg \ \eta_\text{K} \approx -82.6 \ {\rm dB}.$
(11) The same settings apply as in (10) and $r= 0.17$. Vary the cable length up to $l_{\rm blue} = 10 \ \rm km$.
- How much do the maximum value of $\vert H_{\rm E}(f) \vert$, the channel efficiency $\eta_\text{K}$ and the optimal rolloff factor $r_{\rm opt}$ change?
$\Rightarrow\hspace{0.3cm}\text{The maximum value of } \vert H_{\rm E}(f) \vert \text{ increases and }10 \cdot \lg \ \eta_\text{K} \text{ decreases more and more.}$
$\hspace{0.95cm}\text{At 10 km length } 10 \cdot \lg \ \eta_\text{K} \approx -104.9 \ {\rm dB} \text{ and } r_{\rm opt}=0.14\text{. For }f_\star \approx 14.5\ {\rm MHz} \Rightarrow \vert H_{\rm E}(f = f_\star) \vert = 352000 \approx \vert H_{\rm E}(f =0)\vert$.
Applet Manual
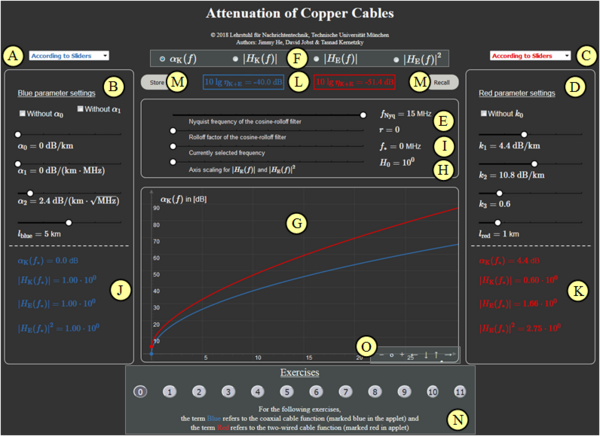
(A) Preselection for blue parameter set
(B) Input of the $\alpha$ parameters via sliders
(C) Preselection for red parameter set
(D) Input of the $k$ parameters via sliders
(E) Input of the parameters $f_{\rm Nyq}$ and $r$
(F) Selection for the graphic display
(G) Display $a_\text{K}(f)$, $|H_\text{K}(f)|$, $|H_\text{E}(f)|$, ...
(H) Scaling factor $H_0$ for $|H_\text{E}(f)|$, $|H_\text{E}(f)|^2$
(I) Selection of the frequency $f_\star$ for numeric values
(J) Numeric values for blue parameter set
(K) Numeric values for red parameter set
(L) Output system efficiency $\eta_\text{K+E}$ in dB
(M) Store & Recall of settings
(N) Exercise section
(O) Variation of the graphic display:$\hspace{0.5cm}$"$+$" (Zoom in), $\hspace{0.5cm}$ "$-$" (Zoom out) $\hspace{0.5cm}$ "$\rm o$" (Reset) $\hspace{0.5cm}$ "$\leftarrow$" (Move left), etc.
Other options for graphic display:
- Hold shift and scroll: Zoom in on/out of coordinate system,
- Hold shift and left click: Move the coordinate system.
About the Authors
This interactive calculation was designed and realized at the Lehrstuhl für Nachrichtentechnik of the Technische Universität München.
- The original version was created in 2009 by Sebastian Seitz as part of his Diploma thesis using "FlashMX–Actionscript" (Supervisor: Günter Söder ).
- In 2018 this Applet was redesigned and updated to "HTML5" by Jimmy He as part of his Bachelor's thesis (Supervisor: Tasnád Kernetzky) .
Once again: Open Applet in new Tab
- ↑ 1.0 1.1 Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.
- ↑ 2.0 2.1 Pollakowski, M.; Wellhausen, H.W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Mitteilung aus dem Forschungs- und Technologiezentrum der Deutschen Telekom AG, Darmstadt, Verlag für Wissenschaft und Leben Georg Heidecker, 1995.