Difference between revisions of "Information Theory/Differential Entropy"
| (61 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Information Theory for Continuous Random Variables |
|Vorherige Seite=Anwendung auf die Digitalsignalübertragung | |Vorherige Seite=Anwendung auf die Digitalsignalübertragung | ||
| − | |Nächste Seite= | + | |Nächste Seite=AWGN_Channel_Capacity_for_Continuous-Valued_Input |
}} | }} | ||
| − | == # | + | == # OVERVIEW OF THE FOURTH MAIN CHAPTER # == |
<br> | <br> | ||
| − | + | In the last chapter of this book, the information-theoretical quantities defined so far for the discrete case are adapted in such a way that they can also be applied to continuous random quantities. | |
| − | * | + | *For example, the entropy $H(X)$ for the discrete random variable $X$ becomes the »differential entropy« $h(X)$ in the continuous case. |
| − | * | + | |
| + | *While $H(X)$ indicates the »uncertainty« with regard to the discrete random variable $X$; in the continuous case $h(X)$ cannot be interpreted in the same way. | ||
| − | + | Many of the relationships derived in the third chapter »Information between two discrete random variables« for conventional entropy also apply to differential entropy. Thus, the differential joint entropy $h(XY)$ can also be given for continuous random variables $X$ and $Y$, and likewise also the two conditional differential entropies $h(Y|X)$ and $h(X|Y)$. | |
| − | + | In detail, this main chapter deals with | |
| − | + | #the special features of »continuous random variables«, | |
| − | + | #the »definition and calculation of the differential entropy« as well as its properties, | |
| − | + | #the »mutual information« between two continuous random variables, | |
| − | + | #the »capacity of the AWGN channel« and several such parallel Gaussian channels, | |
| − | + | #the »channel coding theorem«, one of the highlights of Shannon's information theory, | |
| − | + | #the »AWGN channel capacity« for discrete input $($BPSK, QPSK$)$. | |
| − | == | + | ==Properties of continuous random variables== |
<br> | <br> | ||
| − | + | Up to now, "discrete random variables" of the form $X = \{x_1,\ x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm} , x_μ, \text{...} ,\ x_M\}$ have always been considered, which from an information-theoretical point of view are completely characterized by their [[Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables#Probability_mass_function_and_probability_density_function|"probability mass function"]] $\rm (PMF)$: | |
:$$P_X(X) = \big [ \hspace{0.1cm} | :$$P_X(X) = \big [ \hspace{0.1cm} | ||
p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_{\mu},\hspace{0.05cm} \text{...}\hspace{0.15cm}, p_M \hspace{0.1cm}\big ] | p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_{\mu},\hspace{0.05cm} \text{...}\hspace{0.15cm}, p_M \hspace{0.1cm}\big ] | ||
| − | \hspace{0.3cm}{\rm | + | \hspace{0.3cm}{\rm with} \hspace{0.3cm} p_{\mu}= P_X(x_{\mu})= {\rm Pr}( X = x_{\mu}) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | A "continuous random variable", on the other hand, can assume any value – at least in finite intervals: | |
| − | * | + | * Due to the uncountable supply of values, the description by a probability mass function is not possible in this case, or at least it does not make sense: |
| − | * | + | *This would result in the symbol set size $M \to ∞$ as well as probabilities $p_1 \to 0$, $p_2 \to 0$, etc. |
| − | + | For the description of continuous random variables, one uses equally according to the definitions in the book [[Theory of Stochastic Signals|"Theory of Stochastic Signals"]]: | |
| − | [[File: | + | [[File:EN_Inf_T_4_1_S1b.png|right|frame|PDF and CDF of a continuous random variable]] |
| − | * | + | * the [[Theory_of_Stochastic_Signals/Wahrscheinlichkeitsdichtefunktion_(WDF)|"probability density function"]] $\rm (PDF)$: |
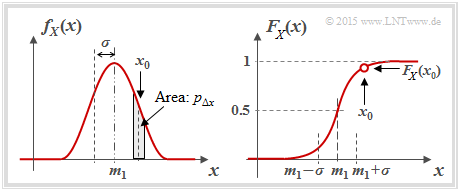
:$$f_X(x_0)= \lim_{{\rm \Delta} x\to \rm 0}\frac{p_{{\rm \Delta} x}}{{\rm \Delta} x} = \lim_{{\rm \Delta} x\to \rm 0}\frac{{\rm Pr} \{ x_0- {\rm \Delta} x/\rm 2 \le \it X \le x_{\rm 0} +{\rm \Delta} x/\rm 2\}}{{\rm \Delta} x};$$ | :$$f_X(x_0)= \lim_{{\rm \Delta} x\to \rm 0}\frac{p_{{\rm \Delta} x}}{{\rm \Delta} x} = \lim_{{\rm \Delta} x\to \rm 0}\frac{{\rm Pr} \{ x_0- {\rm \Delta} x/\rm 2 \le \it X \le x_{\rm 0} +{\rm \Delta} x/\rm 2\}}{{\rm \Delta} x};$$ | ||
| − | :In | + | :In words: the PDF value at $x_0$ gives the probability $p_{Δx}$ that $X$ lies in an (infinitely small) interval of width $Δx$ around $x_0$ , divided by $Δx$ (note the entries in the adjacent graph); |
| − | * | + | *the [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments#Moment_calculation_as_ensemble_average|"mean value"]] (first moment): |
:$$m_1 = {\rm E}\big[ X \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} x \cdot f_X(x) \hspace{0.1cm}{\rm d}x | :$$m_1 = {\rm E}\big[ X \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} x \cdot f_X(x) \hspace{0.1cm}{\rm d}x | ||
\hspace{0.05cm};$$ | \hspace{0.05cm};$$ | ||
| − | * | + | *the [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments#Some_common_central_moments|"variance"]] (second central moment): |
:$$\sigma^2 = {\rm E}\big[(X- m_1 )^2 \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} (x- m_1 )^2 \cdot f_X(x- m_1 ) \hspace{0.1cm}{\rm d}x | :$$\sigma^2 = {\rm E}\big[(X- m_1 )^2 \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} (x- m_1 )^2 \cdot f_X(x- m_1 ) \hspace{0.1cm}{\rm d}x | ||
\hspace{0.05cm};$$ | \hspace{0.05cm};$$ | ||
| − | * | + | *the [[Theory_of_Stochastic_Signals/Cumulative_Distribution_Function|"cumulative distribution function"]] $\rm (CDF)$: |
:$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi | :$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi | ||
| Line 66: | Line 67: | ||
{\rm Pr}(X \le x)\hspace{0.05cm}.$$ | {\rm Pr}(X \le x)\hspace{0.05cm}.$$ | ||
| − | + | Note that both the PDF area and the CDF final value are always equal to $1$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Nomenclature notes on PDF and CDF:}$ |
| + | |||
| + | We use in this chapter for a »'''probability density function'''« $\rm (PDF)$ the representation form $f_X(x)$ often used in the literature, where holds: | ||
| + | *$X$ denotes the (discrete or continuous) random variable, | ||
| + | |||
| + | *$x$ is a possible realization of $X$ ⇒ $x ∈ X$. | ||
| − | |||
| − | |||
| − | |||
| + | Accordingly, we denote the »'''cumulative distribution function'''« $\rm (CDF)$ of the random variable $X$ by $F_X(x)$ according to the following definition: | ||
| − | |||
:$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi | :$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi | ||
\hspace{0.2cm} = \hspace{0.2cm} | \hspace{0.2cm} = \hspace{0.2cm} | ||
{\rm Pr}(X \le x)\hspace{0.05cm}.$$ | {\rm Pr}(X \le x)\hspace{0.05cm}.$$ | ||
| − | In | + | In other $\rm LNTwww$ books, we often write so as not to use up two characters for one variable: |
| − | * | + | *For the PDF $f_x(x)$ ⇒ no distinction between random variable and realization. |
| − | * | + | |
| + | *For the CDF $F_x(r) = {\rm Pr}(x ≤ r)$ ⇒ here one needs a second variable in any case. | ||
| − | + | We apologize for this formal inaccuracy.}} | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ We now consider with the »'''uniform distribution'''« an important special case. |
| − | [[File: | + | |
| − | * | + | [[File:EN_Inf_T_4_1_S1.png|right|frame|Two analog signals as examples of continuous random variables]] |
| − | * | + | |
| + | *The graph shows the course of two uniformly distributed variables, which can assume all values between $1$ and $5$ $($mean value $m_1 = 3)$ with equal probability. | ||
| + | |||
| + | *On the left is the result of a random process, on the right a deterministic signal with the same amplitude distribution. | ||
| − | [[File:P_ID2870__Inf_A_4_1a.png|right|frame| | + | [[File:P_ID2870__Inf_A_4_1a.png|right|frame|PDF and CDF of an uniformly distributed random variable]] |
| − | <br> | + | |
| + | <br>The "probability density function" $\rm (PDF)$ of the uniform distribution has the course sketched in the second graph above: | ||
| − | :$$f_X(x) = \left\{ \begin{array}{c} \hspace{0.25cm}(x_{\rm max} - x_{\rm min})^{-1} \\ 1/2 \cdot (x_{\rm max} - x_{\rm min})^{-1} \\ \hspace{0.25cm} 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{ | + | :$$f_X(x) = \left\{ \begin{array}{c} \hspace{0.25cm}(x_{\rm max} - x_{\rm min})^{-1} \\ 1/2 \cdot (x_{\rm max} - x_{\rm min})^{-1} \\ \hspace{0.25cm} 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{for} } \\ {\rm{for} } \\ {\rm{for} } \\ \end{array} |
| − | \begin{array}{*{20}l} {x_{\rm min} < x < x_{\rm max},} \\ x ={x_{\rm min} \hspace{0. | + | \begin{array}{*{20}l} {x_{\rm min} < x < x_{\rm max},} \\ x ={x_{\rm min} \hspace{0.15cm}{\rm and}\hspace{0.15cm}x = x_{\rm max},} \\ x > x_{\rm max}. \\ \end{array}$$ |
| − | + | The following equations are obtained here for the mean $m_1 ={\rm E}\big[X\big]$ and the variance $σ^2={\rm E}\big[(X – m_1)^2\big]$ : | |
:$$m_1 = \frac{x_{\rm max} + x_{\rm min} }{2}\hspace{0.05cm}, $$ | :$$m_1 = \frac{x_{\rm max} + x_{\rm min} }{2}\hspace{0.05cm}, $$ | ||
:$$\sigma^2 = \frac{(x_{\rm max} - x_{\rm min})^2}{12}\hspace{0.05cm}.$$ | :$$\sigma^2 = \frac{(x_{\rm max} - x_{\rm min})^2}{12}\hspace{0.05cm}.$$ | ||
| − | + | Shown below is the »'''cumulative distribution function'''« $\rm (CDF)$: | |
:$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi | :$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi | ||
| Line 112: | Line 120: | ||
{\rm Pr}(X \le x)\hspace{0.05cm}.$$ | {\rm Pr}(X \le x)\hspace{0.05cm}.$$ | ||
| − | * | + | *This is identically zero for $x ≤ x_{\rm min}$, increases linearly thereafter and reaches the CDF final value of $1$ at $x = x_{\rm max}$ . |
| − | * | + | |
| + | *The probability that the random variable $X$ takes on a value between $3$ and $4$ can be determined from both the PDF and the CDF: | ||
:$${\rm Pr}(3 \le X \le 4) = \int_{3}^{4} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi = 0.25\hspace{0.05cm}\hspace{0.05cm},$$ | :$${\rm Pr}(3 \le X \le 4) = \int_{3}^{4} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi = 0.25\hspace{0.05cm}\hspace{0.05cm},$$ | ||
:$${\rm Pr}(3 \le X \le 4) = F_X(4) - F_X(3) = 0.25\hspace{0.05cm}.$$ | :$${\rm Pr}(3 \le X \le 4) = F_X(4) - F_X(3) = 0.25\hspace{0.05cm}.$$ | ||
| − | + | Furthermore, note: | |
| − | * | + | *The result $X = 0$ is excluded for this random variable ⇒ ${\rm Pr}(X = 0) = 0$. |
| − | * | + | |
| + | *The result $X = 4$ , on the other hand, is quite possible. Nevertheless, ${\rm Pr}(X = 4) = 0 $ also applies here.}} | ||
| − | == | + | ==Entropy of continuous random variables after quantization == |
<br> | <br> | ||
| − | + | We now consider a continuous random variable $X$ in the range $0 \le x \le 1$. | |
| − | * | + | *We quantize this random variable $X$, in order to be able to further apply the previous entropy calculation. We call the resulting discrete (quantized) quantity $Z$. |
| − | * | + | |
| − | * | + | *Let the number of quantization steps be $M$, so that each quantization interval $μ$ has the width ${\it Δ} = 1/M$ in the present PDF. We denote the interval centres by $x_μ$. |
| − | * | + | |
| + | *The probability $p_μ = {\rm Pr}(Z = z_μ)$ with respect to $Z$ is equal to the probability that the random variable $X$ has a value between $x_μ - {\it Δ}/2$ and $x_μ + {\it Δ}/2$. | ||
| + | |||
| + | *First we set $M = 2$ and then double this value in each iteration. This makes the quantization increasingly finer. In the $n$th try, then apply $M = 2^n$ and ${\it Δ} =2^{–n}$. | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ The graph shows the results of the first three trials for an asymmetrical triangular PDF $($betweeen $0$ and $1)$: |
| − | [[File: | + | [[File:EN_Inf_T_4_1_S2.png|right|frame|Entropy determination of the triangular PDF after quantization]] |
* $n = 1 \ ⇒ \ M = 2 \ ⇒ \ {\it Δ} = 1/2\text{:}$ $H(Z) = 0.811\ \rm bit,$ | * $n = 1 \ ⇒ \ M = 2 \ ⇒ \ {\it Δ} = 1/2\text{:}$ $H(Z) = 0.811\ \rm bit,$ | ||
* $n = 2 \ ⇒ \ M = 4 \ ⇒ \ {\it Δ} = 1/4\text{:}$ $H(Z) = 1.749\ \rm bit,$ | * $n = 2 \ ⇒ \ M = 4 \ ⇒ \ {\it Δ} = 1/4\text{:}$ $H(Z) = 1.749\ \rm bit,$ | ||
| Line 138: | Line 151: | ||
| − | + | Additionally, the following quantities can be taken from the graph, for example for ${\it Δ} = 1/8$: | |
| − | + | *The interval centres are at | |
| − | |||
| − | * | ||
:$$x_1 = 1/16,\ x_2 = 3/16,\text{ ...} \ ,\ x_8 = 15/16 $$ | :$$x_1 = 1/16,\ x_2 = 3/16,\text{ ...} \ ,\ x_8 = 15/16 $$ | ||
:$$ ⇒ \ x_μ = {\it Δ} · (μ - 1/2).$$ | :$$ ⇒ \ x_μ = {\it Δ} · (μ - 1/2).$$ | ||
| − | * | + | *The interval areas result in |
:$$p_μ = {\it Δ} · f_X(x_μ) ⇒ p_8 = 1/8 · (7/8+1)/2 = 15/64.$$ | :$$p_μ = {\it Δ} · f_X(x_μ) ⇒ p_8 = 1/8 · (7/8+1)/2 = 15/64.$$ | ||
| − | * | + | *Thus, we obtain for the $\rm PMF$ of the quantized random variable $Z$: |
:$$P_Z(Z) = (1/64, \ 3/64, \ 5/64, \ 7/64, \ 9/64, \ 11/64, \ 13/64, \ 15/64).$$}} | :$$P_Z(Z) = (1/64, \ 3/64, \ 5/64, \ 7/64, \ 9/64, \ 11/64, \ 13/64, \ 15/64).$$}} | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ |
| − | + | We interpret the results of this experiment as follows: | |
| − | + | #The entropy $H(Z)$ becomes larger and larger as $M$ increases. | |
| − | + | #The limit of $H(Z)$ for $M \to ∞ \ ⇒ \ {\it Δ} → 0$ is infinite. | |
| − | + | #Thus, the entropy $H(X)$ of the continuous random variable $X$ is also infinite. | |
| − | + | #It follows: '''The previous definition of entropy fails for continuous random variables'''.}} | |
| − | + | To verify our empirical result, we assume the following equation: | |
:$$H(Z) = \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} p_{\mu} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\mu}}= \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} {\it \Delta} \cdot f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{{\it \Delta} \cdot f_X(x_{\mu} )}\hspace{0.05cm}.$$ | :$$H(Z) = \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} p_{\mu} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\mu}}= \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} {\it \Delta} \cdot f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{{\it \Delta} \cdot f_X(x_{\mu} )}\hspace{0.05cm}.$$ | ||
| − | + | *We now split $H(Z) = S_1 + S_2$ into two summands: | |
:$$\begin{align*}S_1 & = {\rm log}_2 \hspace{0.1cm} \frac{1}{\it \Delta} \cdot \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.02cm} {\it \Delta} \cdot f_X(x_{\mu} ) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.05cm},\\ | :$$\begin{align*}S_1 & = {\rm log}_2 \hspace{0.1cm} \frac{1}{\it \Delta} \cdot \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.02cm} {\it \Delta} \cdot f_X(x_{\mu} ) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.05cm},\\ | ||
| Line 170: | Line 181: | ||
\hspace{0.2cm} \int_{0}^{1} \hspace{0.05cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$ | \hspace{0.2cm} \int_{0}^{1} \hspace{0.05cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$ | ||
| − | * | + | *The approximation $S_1 ≈ -\log_2 {\it Δ}$ applies exactly only in the borderline case ${\it Δ} → 0$. |
| − | * | + | |
| + | *The given approximation for $S_2$ is also only valid for small ${\it Δ} → {\rm d}x$, so that one should replace the sum by the integral. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Generalization:}$ |
| − | + | If one approximates the continuous random variable $X$ with the PDF $f_X(x)$ by a discrete random variable $Z$ by performing a (fine) quantization with the interval width ${\it Δ}$, one obtains for the entropy of the random variable $Z$: | |
:$$H(Z) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm}+ | :$$H(Z) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm}+ | ||
\hspace{-0.35cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x = - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm} + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$ | \hspace{-0.35cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x = - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm} + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$ | ||
| − | + | *The integral describes the [[Information_Theory/Differentielle_Entropie#Definition_and_properties_of_differential_entropy|"differential entropy"]] $h(X)$ of the continuous random variable $X$. | |
| + | |||
| + | For the special case ${\it Δ} = 1/M = 2^{-n}$, the above equation can also be written as follows: | ||
:$$H(Z) = n + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$ | :$$H(Z) = n + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$ | ||
| − | * | + | *In the borderline case ${\it Δ} → 0 \ ⇒ \ M → ∞ \ ⇒ \ n → ∞$, the entropy of the continuous random variable is also infinite: $H(X) → ∞$. |
| − | * | + | *For each $n$ the equation $H(Z) = n$ is only an approximation, where the differential entropy $h(X)$ of the continuous quantity serves as a correction factor. |
| + | }} | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ As in $\text{Example 2}$, we consider a asymmetrical triangular PDF $($between $0$ and $1)$. Its differential entropy, as calculated in [[Aufgaben:Exercise_4.2:_Triangular_PDF|"Exercise 4.2"]] results in |
| − | [[File: | + | [[File:EN_Inf_T_4_1_S2c.png|right|frame|Entropy of the asymmetrical triangular PDF after quantization ]] |
:$$h(X) = \hspace{0.05cm}-0.279 \ \rm bit.$$ | :$$h(X) = \hspace{0.05cm}-0.279 \ \rm bit.$$ | ||
| − | * | + | * The table shows the entropy $H(Z)$ of the quantity $Z$ quantized with $n$ bits. |
| − | * | + | *Already fo $n = 3$ one can see a good agreement between the approximation (lower row) and the exact calculation (row 2). |
| − | * | + | *For $n = 10$, the approximation will agree even better with the exact calculation (which is extremely time-consuming. |
}} | }} | ||
| − | ==Definition | + | ==Definition and properties of differential entropy == |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Generalization:}$ |
| − | + | The »'''differential entropy'''« $h(X)$ of a continuous value random variable $X$ with probability density function $f_X(x)$ is: | |
:$$h(X) = | :$$h(X) = | ||
\hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[ f_X(x) \big] \hspace{0.1cm}{\rm d}x | \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[ f_X(x) \big] \hspace{0.1cm}{\rm d}x | ||
| − | \hspace{0.6cm}{\rm | + | \hspace{0.6cm}{\rm with}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | A pseudo-unit must be added in each case: | |
| − | * | + | *"nat" when using "ln" ⇒ natural logarithm, |
| − | |||
| + | *"bit" when using "log<sub>2</sub>" ⇒ binary logarithm.}} | ||
| − | |||
| − | [[File:P_ID2854__Inf_T_4_1_S3a_neu.png|right|frame| | + | While the (conventional) entropy of a discrete random variable $X$ is always $H(X) ≥ 0$ , the differential entropy $h(X)$ of a continuous random variable can also be negative. From this it is already evident that $h(X)$ in contrast to $H(X)$ cannot be interpreted as "uncertainty". |
| + | |||
| + | [[File:P_ID2854__Inf_T_4_1_S3a_neu.png|right|frame|PDF of an uniform distributed random variable]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ |
| − | + | The upper graph shows the $\rm PDF$ of a random variable $X$, which is uniform distributed between $x_{\rm min}$ and $x_{\rm max}$. | |
| + | *For its differential entropy one obtains in "nat": | ||
:$$\begin{align*}h(X) & = - \hspace{-0.18cm}\int\limits_{x_{\rm min} }^{x_{\rm max} } \hspace{-0.28cm} \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \cdot {\rm ln} \hspace{0.1cm}\big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \hspace{0.1cm}{\rm d}x \\ & = | :$$\begin{align*}h(X) & = - \hspace{-0.18cm}\int\limits_{x_{\rm min} }^{x_{\rm max} } \hspace{-0.28cm} \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \cdot {\rm ln} \hspace{0.1cm}\big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \hspace{0.1cm}{\rm d}x \\ & = | ||
{\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \cdot \big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big ]_{x_{\rm min} }^{x_{\rm max} }={\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big]\hspace{0.05cm}.\end{align*} $$ | {\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \cdot \big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big ]_{x_{\rm min} }^{x_{\rm max} }={\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big]\hspace{0.05cm}.\end{align*} $$ | ||
| − | + | *The equation for the differential entropy in "bit" is: | |
:$$h(X) = \log_2 \big[x_{\rm max} – x_{ \rm min} \big].$$ | :$$h(X) = \log_2 \big[x_{\rm max} – x_{ \rm min} \big].$$ | ||
| − | [[File:P_ID2855__Inf_T_4_1_S3b_neu.png|left|frame|$h(X)$ | + | [[File:P_ID2855__Inf_T_4_1_S3b_neu.png|left|frame|$h(X)$ for different rectangular density functions ⇒ uniform distributed random variables]] |
| − | <br><br><br><br> | + | <br><br><br><br>The graph on the left shows the numerical evaluation of the above result by means of some examples. |
}} | }} | ||
| Line 238: | Line 255: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Interpretation:}$ | $\text{Interpretation:}$ | ||
| − | + | From the six sketches in the last example, important properties of the differential entropy $h(X)$ can be read: | |
| − | * | + | *The differential entropy is not changed by a PDF shift $($by $k)$ : |
| − | :$$h(X + k) = h(X) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \text{ | + | :$$h(X + k) = h(X) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \text{For example:} \ \ h_3(X) = h_4(X) = h_5(X) \hspace{0.05cm}.$$ |
| − | * $h(X)$ | + | * $h(X)$ changes by compression/spreading of the PDF by the factor $k ≠ 0$ as follows: |
:$$h( k\hspace{-0.05cm} \cdot \hspace{-0.05cm}X) = h(X) + {\rm log}_2 \hspace{0.05cm} \vert k \vert \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | :$$h( k\hspace{-0.05cm} \cdot \hspace{-0.05cm}X) = h(X) + {\rm log}_2 \hspace{0.05cm} \vert k \vert \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | ||
| − | \text{ | + | \text{For example:} \ \ h_6(X) = h_5(AX) = h_5(X) + {\rm log}_2 \hspace{0.05cm} (A) = |
{\rm log}_2 \hspace{0.05cm} (2A) | {\rm log}_2 \hspace{0.05cm} (2A) | ||
\hspace{0.05cm}.$$}} | \hspace{0.05cm}.$$}} | ||
| − | + | Many of the equations derived in the chapter [[Information_Theory/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen|"Different entropies of two-dimensional random variables"]] for the discrete case also apply to continuous random variables. | |
| − | + | From the following compilation one can see that often only the (large) $H$ has to be replaced by a (small) $h$ as well as the probability mass function $\rm (PMF)$ by the corresponding probability density function $\rm (PDF)$ . | |
| − | * | + | * »'''Conditional Differential Entropy'''«: |
:$$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} | :$$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} | ||
| Line 263: | Line 280: | ||
\hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$ | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$ | ||
| − | * | + | * »'''Joint Differential Entropy'''«: |
:$$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} | :$$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} | ||
| Line 272: | Line 289: | ||
\hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$ | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$ | ||
| − | * ''' | + | * »'''Chain rule'''« of differential entropy: |
:$$H(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} | :$$H(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} | ||
| Line 287: | Line 304: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * ''' | + | * »'''Kullback–Leibler distance'''« between the random variables $X$ and $Y$: |
:$$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{X})\hspace{-0.8cm}} | :$$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{X})\hspace{-0.8cm}} | ||
| Line 297: | Line 314: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | == | + | ==Differential entropy of some peak-constrained random variables == |
<br> | <br> | ||
| − | [[File: | + | [[File:EN_Inf_T_4_1_S4a.png|right|frame|Differential entropy of peak-constrained random variables]] |
| − | + | The table shows the results regarding the differential entropy for three exemplary probability density functions $f_X(x)$. These are all peak-constrained, i.e. $|X| ≤ A$ applies in each case. | |
| − | * | + | *With "peak constraint" , the differential entropy can always be represented as follows: |
| + | :$$h(X) = {\rm log}\,\, ({\it \Gamma}_{\rm A} \cdot A).$$ | ||
| − | + | *Add the pseudo-unit "nat" when using $\ln$ and the pseudo-unit "bit" when using $\log_2$. | |
| + | |||
| + | *${\it \Gamma}_{\rm A}$ depends solely on the PDF form and applies only to "peak limitation" ⇒ German: "Amplitudenbegrenzung" ⇒ Index $\rm A$. | ||
| − | + | *A uniform distribution in the range $|X| ≤ 1$ yields $h(X) = 1$ bit, a second one in the range $|Y| ≤ 4$ to $h(Y) = 3$ bit. | |
| − | |||
| − | |||
<br clear=all> | <br clear=all> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Theorem:}$ | $\text{Theorem:}$ | ||
| − | + | Under the »'''peak contstraint'''« ⇒ i.e. PDF $f_X(x) = 0$ for $ \vert x \vert > A$ – the »'''uniform distribution'''« leads to the maximum differential entropy: | |
:$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} (2A)\hspace{0.05cm}.$$ | :$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} (2A)\hspace{0.05cm}.$$ | ||
| − | + | Here, the appropriate parameter ${\it \Gamma}_{\rm A} = 2$ is maximal. | |
| − | + | You will find the [[Information_Theory/Differential_Entropy#Proof:_Maximum_differential_entropy_with_peak_constraint|$\text{proof}$]] at the end of this chapter.}} | |
| − | + | The theorem simultaneously means that for any other peak-constrained PDF (except the uniform distribution) the characteristic parameter ${\it \Gamma}_{\rm A} < 2$. | |
| − | * | + | *For the symmetric triangular distribution, the above table gives ${\it \Gamma}_{\rm A} = \sqrt{\rm e} ≈ 1.649$. |
| − | * | + | *In contrast, for the one-sided triangle $($between $0$ and $A)$ ${\it \Gamma}_{\rm A}$ is only half as large. |
| − | * | + | *For every other triangle $($width $A$, arbitrary peak between $0$ and $A)$ ${\it \Gamma}_{\rm A} ≈ 0.824$ also applies. |
| − | + | The respective second $h(X)$ specification and the characteristic ${\it \Gamma}_{\rm L}$ on the other hand, are suitable for the comparison of random variables with power constraints, which will be discussed in the next section. Under this constraint, e.g. the symmetric triangular distribution $({\it \Gamma}_{\rm L} ≈ 16.31)$ is better than the uniform distribution $({\it \Gamma}_{\rm L} = 12)$. | |
| − | == | + | ==Differential entropy of some power-constrained random variables == |
<br> | <br> | ||
| − | + | The differential entropies $h(X)$ for three exemplary density functions $f_X(x)$ without boundary, which all have the same variance $σ^2 = {\rm E}\big[|X -m_x|^2 \big]$ and thus the same standard deviation $σ$ through appropriate parameter selection, can be taken from the following table. Considered are: | |
| + | |||
| + | [[File:EN_Inf_T_4_1_S5a_v5.png|right|frame|Differential entropy of power-constrained random variables]] | ||
| + | *the [[Theory_of_Stochastic_Signals/Gaußverteilte_Zufallsgrößen|"Gaussian distribution"]], | ||
| + | |||
| + | *the [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables#Two-sided_exponential_distribution_-_Laplace_distribution|"Laplace distribution"]] ⇒ a two-sided exponential distribution, | ||
| + | |||
| + | *the (one-sided) [[Theory_of_Stochastic_Signals/Exponentialverteilte_Zufallsgrößen#One-sided_exponential_distribution|"exponential distribution"]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | The differential entropy can always be represented here as | ||
| + | :$$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm L} \cdot \sigma^2).$$ | ||
| + | ${\it \Gamma}_{\rm L}$ depends solely on the PDF form and applies only to "power limitation" ⇒ German: "Leistungsbegrenzung" ⇒ Index $\rm L$. | ||
| − | + | The result differs only by the pseudo-unit | |
| − | + | *"nat" when using $\ln$ or | |
| − | + | ||
| − | * | + | *"bit" when using $\log_2$. |
| − | * | ||
<br clear=all> | <br clear=all> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Theorem:}$ | $\text{Theorem:}$ | ||
| − | + | Under the constraint of »'''power constraint'''«, the »'''Gaussian PDF'''«, | |
| − | :$$f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2} } \cdot {\rm | + | :$$f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2} } \cdot {\rm e}^{ |
| − | - \hspace{0.05cm} | + | - \hspace{0.05cm}{(x - m_1)^2}/(2 \sigma^2)},$$ |
| − | + | leads to the maximum differential entropy, independent of the mean $m_1$: | |
:$$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08\hspace{0.05cm}.$$ | :$$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08\hspace{0.05cm}.$$ | ||
| − | + | You will find the [[Information_Theory/Differential_Entropy#Proof:_Maximum_differential_entropy_with_power_constraint|"proof"]] at the end of this chapter.}} | |
| − | + | This statement means at the same time that for any PDF other than the Gaussian distribution, the characteristic value will be ${\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08$. For example, the characteristic value | |
| − | * | + | *for the triangular distribution to ${\it \Gamma}_{\rm L} = 6{\rm e} ≈ 16.31$, |
| − | * | + | |
| − | * | + | *for the Laplace distribution to ${\it \Gamma}_{\rm L} = 2{\rm e}^2 ≈ 14.78$, and |
| + | |||
| + | *for the uniform distribution to ${\it \Gamma}_{\rm L} = 12$ . | ||
| − | == | + | ==Proof: Maximum differential entropy with peak constraint== |
<br> | <br> | ||
| − | + | Under the peak constraint ⇒ $|X| ≤ A$ the differential entropy is: | |
:$$h(X) = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ | :$$h(X) = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ | ||
| − | + | Of all possible probability density functions $f_X(x)$ that satisfy the condition | |
:$$\int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x = 1$$ | :$$\int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x = 1$$ | ||
| − | + | we are now looking for the function $g_X(x)$ that leads to the maximum differential entropy $h(X)$. | |
| − | + | For derivation we use the [https://en.wikipedia.org/wiki/Lagrange_multiplier $»\text{Lagrange multiplier method}$«]: | |
| − | * | + | *We define the Lagrangian parameter $L$ in such a way that it contains both $h(X)$ and the constraint $|X| ≤ A$ : |
:$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.5cm}+ \hspace{0.5cm} | :$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.5cm}+ \hspace{0.5cm} | ||
\lambda \cdot | \lambda \cdot | ||
\int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x | \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *We generally set $f_X(x) = g_X(x) + ε · ε_X(x)$, where $ε_X(x)$ is an arbitrary function, with the restriction that the PDF area must equal $1$. Thus we obtain: |
| − | :$$\begin{align*}L = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} [ g_X(x) + \varepsilon \cdot \varepsilon_X(x) ] \cdot {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) + \varepsilon \cdot \varepsilon_X(x) } \hspace{0.1cm}{\rm d}x + \lambda \cdot | + | :$$\begin{align*}L = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm}\big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x)\big ] \cdot {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) + \varepsilon \cdot \varepsilon_X(x) } \hspace{0.1cm}{\rm d}x + \lambda \cdot |
\int_{-A}^{+A} \hspace{0.05cm} \big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x) \big ] \hspace{0.1cm}{\rm d}x | \int_{-A}^{+A} \hspace{0.05cm} \big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x) \big ] \hspace{0.1cm}{\rm d}x | ||
\hspace{0.05cm}.\end{align*}$$ | \hspace{0.05cm}.\end{align*}$$ | ||
| − | * | + | *The best possible function is obtained when there is a stationary solution for $ε = 0$ : |
:$$\left [\frac{{\rm d}L}{{\rm d}\varepsilon} \right ]_{\varepsilon \hspace{0.05cm}= \hspace{0.05cm}0}=\hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \cdot \big [ {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 \big ]\hspace{0.1cm}{\rm d}x \hspace{0.3cm} + \hspace{0.3cm}\lambda \cdot | :$$\left [\frac{{\rm d}L}{{\rm d}\varepsilon} \right ]_{\varepsilon \hspace{0.05cm}= \hspace{0.05cm}0}=\hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \cdot \big [ {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 \big ]\hspace{0.1cm}{\rm d}x \hspace{0.3cm} + \hspace{0.3cm}\lambda \cdot | ||
\int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \hspace{0.1cm}{\rm d}x \stackrel{!}{=} 0 | \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \hspace{0.1cm}{\rm d}x \stackrel{!}{=} 0 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *This conditional equation can be satisfied independently of $ε_X$ only if holds: |
:$${\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 + \lambda = 0 \hspace{0.4cm} | :$${\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 + \lambda = 0 \hspace{0.4cm} | ||
| − | \forall x \in [-A, +A]\hspace{0.3cm} \Rightarrow\hspace{0.3cm} | + | \forall x \in \big[-A, +A \big]\hspace{0.3cm} \Rightarrow\hspace{0.3cm} |
g_X(x) = {\rm const.}\hspace{0.4cm} | g_X(x) = {\rm const.}\hspace{0.4cm} | ||
| − | \forall x \in [-A, +A]\hspace{0.05cm}.$$ | + | \forall x \in \big [-A, +A \big]\hspace{0.05cm}.$$ |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Summary for peak constraints:}$ |
| − | + | The maximum differential entropy is obtained under the constraint $ \vert X \vert ≤ A$ for the »'''uniform PDF'''«: | |
:$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm A} \cdot A) = {\rm log} \hspace{0.1cm} (2A) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm A} = 2 | :$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm A} \cdot A) = {\rm log} \hspace{0.1cm} (2A) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm A} = 2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Any other random variable with the PDF property $f_X(\vert x \vert > A) = 0$ leads to a smaller differential entropy, characterized by the parameter ${\it \Gamma}_{\rm A} < 2$.}} | |
| − | == | + | ==Proof: Maximum differential entropy with power constraint== |
<br> | <br> | ||
| − | + | Let's start by explaining the term: | |
| − | * | + | *Actually, it is not the power ⇒ the [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments#Moment_calculation_as_ensemble_average|"second moment"]] $m_2$ that is limited, but the [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments#Some_common_central_moments|"second central moment"]] ⇒ variance $μ_2 = σ^2$. |
| − | * | + | |
| − | * | + | *We are now looking for the maximum differential entropy under the constraint ${\rm E}\big[|X - m_1|^2 \big] ≤ σ^2$. |
| + | *Here we may replace the "smaller/equal sign" by the "equal sign". | ||
| − | + | If we only allow mean-free random variables, we circumvent the problem. Thus the [https://en.wikipedia.org/wiki/Lagrange_multiplier "Lagrange multiplier"]: | |
:$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} | :$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} | ||
| Line 413: | Line 439: | ||
\int_{-\infty}^{+\infty}\hspace{-0.1cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ | \int_{-\infty}^{+\infty}\hspace{-0.1cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ | ||
| − | + | Following a similar procedure as in the [[Information_Theory/Differentielle_Entropie#Proof:_Maximum_differential_entropy_with_peak_constraint|"proof of the peak constraint"]] it turns out, that the "best possible" function must be $g_X(x) \sim {\rm e}^{–λ_2\hspace{0.05cm} · \hspace{0.05cm} x^2}$ ⇒ [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables|"Gaussian distribution"]]: | |
:$$g_X(x) ={1}/{\sqrt{2\pi \sigma^2}} \cdot {\rm e}^{ | :$$g_X(x) ={1}/{\sqrt{2\pi \sigma^2}} \cdot {\rm e}^{ | ||
- \hspace{0.05cm}{x^2}/{(2 \sigma^2)} }\hspace{0.05cm}.$$ | - \hspace{0.05cm}{x^2}/{(2 \sigma^2)} }\hspace{0.05cm}.$$ | ||
| − | + | However, we use here for the explicit proof the [[Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables#Informational_divergence_-_Kullback-Leibler_distance|"Kullback–Leibler distance"]] between a suitable general PDF $f_X(x)$ and the Gaussian PDF $g_X(x)$: | |
:$$D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = \int_{-\infty}^{+\infty} \hspace{0.02cm} | :$$D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = \int_{-\infty}^{+\infty} \hspace{0.02cm} | ||
| Line 425: | Line 451: | ||
f_X(x) \cdot {\rm ln} \hspace{0.1cm} {g_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ | f_X(x) \cdot {\rm ln} \hspace{0.1cm} {g_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ | ||
| − | + | For simplicity, the natural logarithm ⇒ $\ln$ is used here. Thus we obtain for the second integral: | |
:$$I_2 = - \frac{1}{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{-0.4cm} f_X(x) \hspace{0.1cm}{\rm d}x | :$$I_2 = - \frac{1}{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{-0.4cm} f_X(x) \hspace{0.1cm}{\rm d}x | ||
| Line 432: | Line 458: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | By definition, the first integral is equal to $1$ and the second integral gives $σ^2$: | |
:$$I_2 = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) - {1}/{2} \cdot [{\rm ln} \hspace{0.1cm} ({\rm e})] = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)$$ | :$$I_2 = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) - {1}/{2} \cdot [{\rm ln} \hspace{0.1cm} ({\rm e})] = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)$$ | ||
| Line 438: | Line 464: | ||
-h(X) + {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$ | -h(X) + {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$ | ||
| − | + | Since also for continuous random variables the Kullback-Leibler distance is always $\ge 0$ , after generalization ("ln" ⇒ "log"): | |
:$$h(X) \le {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$ | :$$h(X) \le {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$ | ||
| − | + | The equal sign only applies if the random variable $X$ is Gaussian distributed. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Summary for power constraints:}$ |
| − | + | The maximum differential entropy is obtained under the condition ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ independent of $m_1$ for the »'''Gaussian PDF'''«: | |
:$$h_{\rm max}(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm} \rm L} \cdot \sigma^2) = | :$$h_{\rm max}(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm} \rm L} \cdot \sigma^2) = | ||
{1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm L} = 2\pi{\rm e} | {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm L} = 2\pi{\rm e} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Any other continuous random variable $X$ with variance ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ leads to a smaller value, characterized by the parameter ${\it \Gamma}_{\rm L} < 2πe$. }} | |
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.1:_PDF,_CDF_and_Probability|Exercise 4.1: PDF, CDF and Probability]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.1Z:_Calculation_of_Moments|Exercise 4.1Z: Calculation of Moments]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.2:_Triangular_PDF|Exercise 4.2: Triangular PDF]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.2Z:_Mixed_Random_Variables|Exercise 4.2Z: Mixed Random Variables]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.3:_PDF_Comparison_with_Regard_to_Differential_Entropy|Exercise 4.3: PDF Comparison with Regard to Differential Entropy]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.3Z:_Exponential_and_Laplace_Distribution|Exercise 4.3Z: Exponential and Laplace Distribution]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.4:_Conventional_Entropy_and_Differential_Entropy|Exercise 4.4: Conventional Entropy and Differential Entropy]] |
Latest revision as of 14:29, 28 February 2023
Contents
- 1 # OVERVIEW OF THE FOURTH MAIN CHAPTER #
- 2 Properties of continuous random variables
- 3 Entropy of continuous random variables after quantization
- 4 Definition and properties of differential entropy
- 5 Differential entropy of some peak-constrained random variables
- 6 Differential entropy of some power-constrained random variables
- 7 Proof: Maximum differential entropy with peak constraint
- 8 Proof: Maximum differential entropy with power constraint
- 9 Exercises for the chapter
# OVERVIEW OF THE FOURTH MAIN CHAPTER #
In the last chapter of this book, the information-theoretical quantities defined so far for the discrete case are adapted in such a way that they can also be applied to continuous random quantities.
- For example, the entropy $H(X)$ for the discrete random variable $X$ becomes the »differential entropy« $h(X)$ in the continuous case.
- While $H(X)$ indicates the »uncertainty« with regard to the discrete random variable $X$; in the continuous case $h(X)$ cannot be interpreted in the same way.
Many of the relationships derived in the third chapter »Information between two discrete random variables« for conventional entropy also apply to differential entropy. Thus, the differential joint entropy $h(XY)$ can also be given for continuous random variables $X$ and $Y$, and likewise also the two conditional differential entropies $h(Y|X)$ and $h(X|Y)$.
In detail, this main chapter deals with
- the special features of »continuous random variables«,
- the »definition and calculation of the differential entropy« as well as its properties,
- the »mutual information« between two continuous random variables,
- the »capacity of the AWGN channel« and several such parallel Gaussian channels,
- the »channel coding theorem«, one of the highlights of Shannon's information theory,
- the »AWGN channel capacity« for discrete input $($BPSK, QPSK$)$.
Properties of continuous random variables
Up to now, "discrete random variables" of the form $X = \{x_1,\ x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm} , x_μ, \text{...} ,\ x_M\}$ have always been considered, which from an information-theoretical point of view are completely characterized by their "probability mass function" $\rm (PMF)$:
- $$P_X(X) = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_{\mu},\hspace{0.05cm} \text{...}\hspace{0.15cm}, p_M \hspace{0.1cm}\big ] \hspace{0.3cm}{\rm with} \hspace{0.3cm} p_{\mu}= P_X(x_{\mu})= {\rm Pr}( X = x_{\mu}) \hspace{0.05cm}.$$
A "continuous random variable", on the other hand, can assume any value – at least in finite intervals:
- Due to the uncountable supply of values, the description by a probability mass function is not possible in this case, or at least it does not make sense:
- This would result in the symbol set size $M \to ∞$ as well as probabilities $p_1 \to 0$, $p_2 \to 0$, etc.
For the description of continuous random variables, one uses equally according to the definitions in the book "Theory of Stochastic Signals":
- the "probability density function" $\rm (PDF)$:
- $$f_X(x_0)= \lim_{{\rm \Delta} x\to \rm 0}\frac{p_{{\rm \Delta} x}}{{\rm \Delta} x} = \lim_{{\rm \Delta} x\to \rm 0}\frac{{\rm Pr} \{ x_0- {\rm \Delta} x/\rm 2 \le \it X \le x_{\rm 0} +{\rm \Delta} x/\rm 2\}}{{\rm \Delta} x};$$
- In words: the PDF value at $x_0$ gives the probability $p_{Δx}$ that $X$ lies in an (infinitely small) interval of width $Δx$ around $x_0$ , divided by $Δx$ (note the entries in the adjacent graph);
- the "mean value" (first moment):
- $$m_1 = {\rm E}\big[ X \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} x \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm};$$
- the "variance" (second central moment):
- $$\sigma^2 = {\rm E}\big[(X- m_1 )^2 \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} (x- m_1 )^2 \cdot f_X(x- m_1 ) \hspace{0.1cm}{\rm d}x \hspace{0.05cm};$$
- the "cumulative distribution function" $\rm (CDF)$:
- $$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$
Note that both the PDF area and the CDF final value are always equal to $1$.
$\text{Nomenclature notes on PDF and CDF:}$
We use in this chapter for a »probability density function« $\rm (PDF)$ the representation form $f_X(x)$ often used in the literature, where holds:
- $X$ denotes the (discrete or continuous) random variable,
- $x$ is a possible realization of $X$ ⇒ $x ∈ X$.
Accordingly, we denote the »cumulative distribution function« $\rm (CDF)$ of the random variable $X$ by $F_X(x)$ according to the following definition:
- $$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$
In other $\rm LNTwww$ books, we often write so as not to use up two characters for one variable:
- For the PDF $f_x(x)$ ⇒ no distinction between random variable and realization.
- For the CDF $F_x(r) = {\rm Pr}(x ≤ r)$ ⇒ here one needs a second variable in any case.
We apologize for this formal inaccuracy.
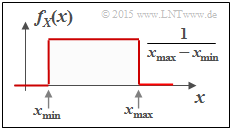
$\text{Example 1:}$ We now consider with the »uniform distribution« an important special case.
- The graph shows the course of two uniformly distributed variables, which can assume all values between $1$ and $5$ $($mean value $m_1 = 3)$ with equal probability.
- On the left is the result of a random process, on the right a deterministic signal with the same amplitude distribution.
The "probability density function" $\rm (PDF)$ of the uniform distribution has the course sketched in the second graph above:
- $$f_X(x) = \left\{ \begin{array}{c} \hspace{0.25cm}(x_{\rm max} - x_{\rm min})^{-1} \\ 1/2 \cdot (x_{\rm max} - x_{\rm min})^{-1} \\ \hspace{0.25cm} 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{for} } \\ {\rm{for} } \\ {\rm{for} } \\ \end{array} \begin{array}{*{20}l} {x_{\rm min} < x < x_{\rm max},} \\ x ={x_{\rm min} \hspace{0.15cm}{\rm and}\hspace{0.15cm}x = x_{\rm max},} \\ x > x_{\rm max}. \\ \end{array}$$
The following equations are obtained here for the mean $m_1 ={\rm E}\big[X\big]$ and the variance $σ^2={\rm E}\big[(X – m_1)^2\big]$ :
- $$m_1 = \frac{x_{\rm max} + x_{\rm min} }{2}\hspace{0.05cm}, $$
- $$\sigma^2 = \frac{(x_{\rm max} - x_{\rm min})^2}{12}\hspace{0.05cm}.$$
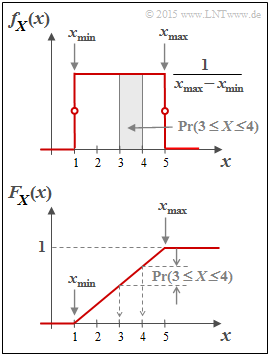
Shown below is the »cumulative distribution function« $\rm (CDF)$:
- $$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$
- This is identically zero for $x ≤ x_{\rm min}$, increases linearly thereafter and reaches the CDF final value of $1$ at $x = x_{\rm max}$ .
- The probability that the random variable $X$ takes on a value between $3$ and $4$ can be determined from both the PDF and the CDF:
- $${\rm Pr}(3 \le X \le 4) = \int_{3}^{4} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi = 0.25\hspace{0.05cm}\hspace{0.05cm},$$
- $${\rm Pr}(3 \le X \le 4) = F_X(4) - F_X(3) = 0.25\hspace{0.05cm}.$$
Furthermore, note:
- The result $X = 0$ is excluded for this random variable ⇒ ${\rm Pr}(X = 0) = 0$.
- The result $X = 4$ , on the other hand, is quite possible. Nevertheless, ${\rm Pr}(X = 4) = 0 $ also applies here.
Entropy of continuous random variables after quantization
We now consider a continuous random variable $X$ in the range $0 \le x \le 1$.
- We quantize this random variable $X$, in order to be able to further apply the previous entropy calculation. We call the resulting discrete (quantized) quantity $Z$.
- Let the number of quantization steps be $M$, so that each quantization interval $μ$ has the width ${\it Δ} = 1/M$ in the present PDF. We denote the interval centres by $x_μ$.
- The probability $p_μ = {\rm Pr}(Z = z_μ)$ with respect to $Z$ is equal to the probability that the random variable $X$ has a value between $x_μ - {\it Δ}/2$ and $x_μ + {\it Δ}/2$.
- First we set $M = 2$ and then double this value in each iteration. This makes the quantization increasingly finer. In the $n$th try, then apply $M = 2^n$ and ${\it Δ} =2^{–n}$.
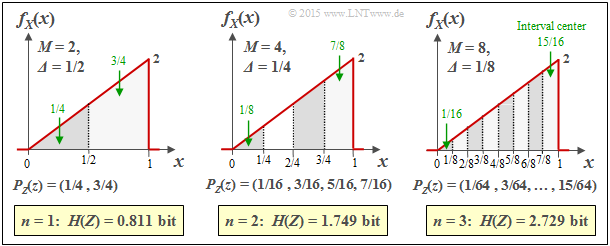
$\text{Example 2:}$ The graph shows the results of the first three trials for an asymmetrical triangular PDF $($betweeen $0$ and $1)$:
- $n = 1 \ ⇒ \ M = 2 \ ⇒ \ {\it Δ} = 1/2\text{:}$ $H(Z) = 0.811\ \rm bit,$
- $n = 2 \ ⇒ \ M = 4 \ ⇒ \ {\it Δ} = 1/4\text{:}$ $H(Z) = 1.749\ \rm bit,$
- $n = 3 \ ⇒ \ M = 8 \ ⇒ \ {\it Δ} = 1/8\text{:}$ $H(Z) = 2.729\ \rm bit.$
Additionally, the following quantities can be taken from the graph, for example for ${\it Δ} = 1/8$:
- The interval centres are at
- $$x_1 = 1/16,\ x_2 = 3/16,\text{ ...} \ ,\ x_8 = 15/16 $$
- $$ ⇒ \ x_μ = {\it Δ} · (μ - 1/2).$$
- The interval areas result in
- $$p_μ = {\it Δ} · f_X(x_μ) ⇒ p_8 = 1/8 · (7/8+1)/2 = 15/64.$$
- Thus, we obtain for the $\rm PMF$ of the quantized random variable $Z$:
- $$P_Z(Z) = (1/64, \ 3/64, \ 5/64, \ 7/64, \ 9/64, \ 11/64, \ 13/64, \ 15/64).$$
$\text{Conclusion:}$ We interpret the results of this experiment as follows:
- The entropy $H(Z)$ becomes larger and larger as $M$ increases.
- The limit of $H(Z)$ for $M \to ∞ \ ⇒ \ {\it Δ} → 0$ is infinite.
- Thus, the entropy $H(X)$ of the continuous random variable $X$ is also infinite.
- It follows: The previous definition of entropy fails for continuous random variables.
To verify our empirical result, we assume the following equation:
- $$H(Z) = \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} p_{\mu} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\mu}}= \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} {\it \Delta} \cdot f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{{\it \Delta} \cdot f_X(x_{\mu} )}\hspace{0.05cm}.$$
- We now split $H(Z) = S_1 + S_2$ into two summands:
- $$\begin{align*}S_1 & = {\rm log}_2 \hspace{0.1cm} \frac{1}{\it \Delta} \cdot \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.02cm} {\it \Delta} \cdot f_X(x_{\mu} ) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.05cm},\\ S_2 & = \hspace{0.05cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x_{\mu} ) } \cdot {\it \Delta} \hspace{0.2cm}\approx \hspace{0.2cm} \int_{0}^{1} \hspace{0.05cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$
- The approximation $S_1 ≈ -\log_2 {\it Δ}$ applies exactly only in the borderline case ${\it Δ} → 0$.
- The given approximation for $S_2$ is also only valid for small ${\it Δ} → {\rm d}x$, so that one should replace the sum by the integral.
$\text{Generalization:}$ If one approximates the continuous random variable $X$ with the PDF $f_X(x)$ by a discrete random variable $Z$ by performing a (fine) quantization with the interval width ${\it Δ}$, one obtains for the entropy of the random variable $Z$:
- $$H(Z) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm}+ \hspace{-0.35cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x = - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm} + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$
- The integral describes the "differential entropy" $h(X)$ of the continuous random variable $X$.
For the special case ${\it Δ} = 1/M = 2^{-n}$, the above equation can also be written as follows:
- $$H(Z) = n + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$
- In the borderline case ${\it Δ} → 0 \ ⇒ \ M → ∞ \ ⇒ \ n → ∞$, the entropy of the continuous random variable is also infinite: $H(X) → ∞$.
- For each $n$ the equation $H(Z) = n$ is only an approximation, where the differential entropy $h(X)$ of the continuous quantity serves as a correction factor.
$\text{Example 3:}$ As in $\text{Example 2}$, we consider a asymmetrical triangular PDF $($between $0$ and $1)$. Its differential entropy, as calculated in "Exercise 4.2" results in
- $$h(X) = \hspace{0.05cm}-0.279 \ \rm bit.$$
- The table shows the entropy $H(Z)$ of the quantity $Z$ quantized with $n$ bits.
- Already fo $n = 3$ one can see a good agreement between the approximation (lower row) and the exact calculation (row 2).
- For $n = 10$, the approximation will agree even better with the exact calculation (which is extremely time-consuming.
Definition and properties of differential entropy
$\text{Generalization:}$ The »differential entropy« $h(X)$ of a continuous value random variable $X$ with probability density function $f_X(x)$ is:
- $$h(X) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[ f_X(x) \big] \hspace{0.1cm}{\rm d}x \hspace{0.6cm}{\rm with}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} \hspace{0.05cm}.$$
A pseudo-unit must be added in each case:
- "nat" when using "ln" ⇒ natural logarithm,
- "bit" when using "log2" ⇒ binary logarithm.
While the (conventional) entropy of a discrete random variable $X$ is always $H(X) ≥ 0$ , the differential entropy $h(X)$ of a continuous random variable can also be negative. From this it is already evident that $h(X)$ in contrast to $H(X)$ cannot be interpreted as "uncertainty".
$\text{Example 4:}$ The upper graph shows the $\rm PDF$ of a random variable $X$, which is uniform distributed between $x_{\rm min}$ and $x_{\rm max}$.
- For its differential entropy one obtains in "nat":
- $$\begin{align*}h(X) & = - \hspace{-0.18cm}\int\limits_{x_{\rm min} }^{x_{\rm max} } \hspace{-0.28cm} \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \cdot {\rm ln} \hspace{0.1cm}\big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \hspace{0.1cm}{\rm d}x \\ & = {\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \cdot \big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big ]_{x_{\rm min} }^{x_{\rm max} }={\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big]\hspace{0.05cm}.\end{align*} $$
- The equation for the differential entropy in "bit" is:
- $$h(X) = \log_2 \big[x_{\rm max} – x_{ \rm min} \big].$$
The graph on the left shows the numerical evaluation of the above result by means of some examples.
$\text{Interpretation:}$ From the six sketches in the last example, important properties of the differential entropy $h(X)$ can be read:
- The differential entropy is not changed by a PDF shift $($by $k)$ :
- $$h(X + k) = h(X) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \text{For example:} \ \ h_3(X) = h_4(X) = h_5(X) \hspace{0.05cm}.$$
- $h(X)$ changes by compression/spreading of the PDF by the factor $k ≠ 0$ as follows:
- $$h( k\hspace{-0.05cm} \cdot \hspace{-0.05cm}X) = h(X) + {\rm log}_2 \hspace{0.05cm} \vert k \vert \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \text{For example:} \ \ h_6(X) = h_5(AX) = h_5(X) + {\rm log}_2 \hspace{0.05cm} (A) = {\rm log}_2 \hspace{0.05cm} (2A) \hspace{0.05cm}.$$
Many of the equations derived in the chapter "Different entropies of two-dimensional random variables" for the discrete case also apply to continuous random variables.
From the following compilation one can see that often only the (large) $H$ has to be replaced by a (small) $h$ as well as the probability mass function $\rm (PMF)$ by the corresponding probability density function $\rm (PDF)$ .
- »Conditional Differential Entropy«:
- $$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm}h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.04cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$
- »Joint Differential Entropy«:
- $$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ P_{XY}(x, y)} \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm}h(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{f_{XY}(X, Y)}\right ] =\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.04cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_{XY}(x, y) } \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$
- »Chain rule« of differential entropy:
- $$H(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} H(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) \le \sum_{i = 1}^{n} H(X_i) \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm} h(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} h(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) \le \sum_{i = 1}^{n} h(X_i) \hspace{0.05cm}.$$
- »Kullback–Leibler distance« between the random variables $X$ and $Y$:
- $$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{X})\hspace{-0.8cm}} P_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{P_X(x)}{P_Y(x)} \ge 0$$
- $$\Rightarrow \hspace{0.3cm}D(f_X \hspace{0.05cm} || \hspace{0.05cm}f_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{f_X(X)}{f_Y(X)}\right ] \hspace{0.2cm}= \hspace{-0.4cm}\int\limits_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{f_X(x)}{f_Y(x)} \hspace{0.15cm}{\rm d}x \ge 0 \hspace{0.05cm}.$$
Differential entropy of some peak-constrained random variables
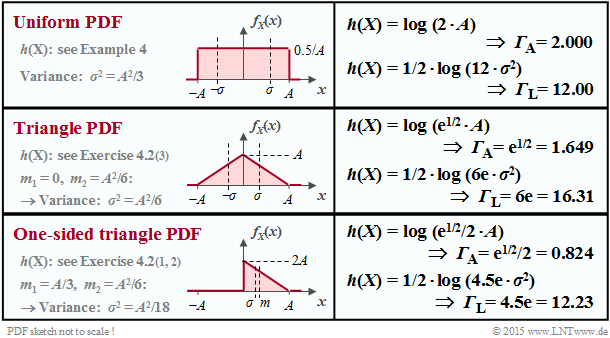
The table shows the results regarding the differential entropy for three exemplary probability density functions $f_X(x)$. These are all peak-constrained, i.e. $|X| ≤ A$ applies in each case.
- With "peak constraint" , the differential entropy can always be represented as follows:
- $$h(X) = {\rm log}\,\, ({\it \Gamma}_{\rm A} \cdot A).$$
- Add the pseudo-unit "nat" when using $\ln$ and the pseudo-unit "bit" when using $\log_2$.
- ${\it \Gamma}_{\rm A}$ depends solely on the PDF form and applies only to "peak limitation" ⇒ German: "Amplitudenbegrenzung" ⇒ Index $\rm A$.
- A uniform distribution in the range $|X| ≤ 1$ yields $h(X) = 1$ bit, a second one in the range $|Y| ≤ 4$ to $h(Y) = 3$ bit.
$\text{Theorem:}$ Under the »peak contstraint« ⇒ i.e. PDF $f_X(x) = 0$ for $ \vert x \vert > A$ – the »uniform distribution« leads to the maximum differential entropy:
- $$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} (2A)\hspace{0.05cm}.$$
Here, the appropriate parameter ${\it \Gamma}_{\rm A} = 2$ is maximal. You will find the $\text{proof}$ at the end of this chapter.
The theorem simultaneously means that for any other peak-constrained PDF (except the uniform distribution) the characteristic parameter ${\it \Gamma}_{\rm A} < 2$.
- For the symmetric triangular distribution, the above table gives ${\it \Gamma}_{\rm A} = \sqrt{\rm e} ≈ 1.649$.
- In contrast, for the one-sided triangle $($between $0$ and $A)$ ${\it \Gamma}_{\rm A}$ is only half as large.
- For every other triangle $($width $A$, arbitrary peak between $0$ and $A)$ ${\it \Gamma}_{\rm A} ≈ 0.824$ also applies.
The respective second $h(X)$ specification and the characteristic ${\it \Gamma}_{\rm L}$ on the other hand, are suitable for the comparison of random variables with power constraints, which will be discussed in the next section. Under this constraint, e.g. the symmetric triangular distribution $({\it \Gamma}_{\rm L} ≈ 16.31)$ is better than the uniform distribution $({\it \Gamma}_{\rm L} = 12)$.
Differential entropy of some power-constrained random variables
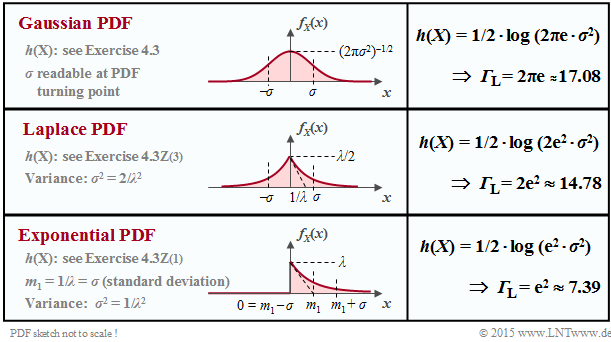
The differential entropies $h(X)$ for three exemplary density functions $f_X(x)$ without boundary, which all have the same variance $σ^2 = {\rm E}\big[|X -m_x|^2 \big]$ and thus the same standard deviation $σ$ through appropriate parameter selection, can be taken from the following table. Considered are:
- the "Laplace distribution" ⇒ a two-sided exponential distribution,
- the (one-sided) "exponential distribution".
The differential entropy can always be represented here as
- $$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm L} \cdot \sigma^2).$$
${\it \Gamma}_{\rm L}$ depends solely on the PDF form and applies only to "power limitation" ⇒ German: "Leistungsbegrenzung" ⇒ Index $\rm L$.
The result differs only by the pseudo-unit
- "nat" when using $\ln$ or
- "bit" when using $\log_2$.
$\text{Theorem:}$ Under the constraint of »power constraint«, the »Gaussian PDF«,
- $$f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2} } \cdot {\rm e}^{ - \hspace{0.05cm}{(x - m_1)^2}/(2 \sigma^2)},$$
leads to the maximum differential entropy, independent of the mean $m_1$:
- $$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08\hspace{0.05cm}.$$
You will find the "proof" at the end of this chapter.
This statement means at the same time that for any PDF other than the Gaussian distribution, the characteristic value will be ${\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08$. For example, the characteristic value
- for the triangular distribution to ${\it \Gamma}_{\rm L} = 6{\rm e} ≈ 16.31$,
- for the Laplace distribution to ${\it \Gamma}_{\rm L} = 2{\rm e}^2 ≈ 14.78$, and
- for the uniform distribution to ${\it \Gamma}_{\rm L} = 12$ .
Proof: Maximum differential entropy with peak constraint
Under the peak constraint ⇒ $|X| ≤ A$ the differential entropy is:
- $$h(X) = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Of all possible probability density functions $f_X(x)$ that satisfy the condition
- $$\int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x = 1$$
we are now looking for the function $g_X(x)$ that leads to the maximum differential entropy $h(X)$.
For derivation we use the $»\text{Lagrange multiplier method}$«:
- We define the Lagrangian parameter $L$ in such a way that it contains both $h(X)$ and the constraint $|X| ≤ A$ :
- $$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.5cm}+ \hspace{0.5cm} \lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
- We generally set $f_X(x) = g_X(x) + ε · ε_X(x)$, where $ε_X(x)$ is an arbitrary function, with the restriction that the PDF area must equal $1$. Thus we obtain:
- $$\begin{align*}L = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm}\big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x)\big ] \cdot {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) + \varepsilon \cdot \varepsilon_X(x) } \hspace{0.1cm}{\rm d}x + \lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} \big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x) \big ] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$
- The best possible function is obtained when there is a stationary solution for $ε = 0$ :
- $$\left [\frac{{\rm d}L}{{\rm d}\varepsilon} \right ]_{\varepsilon \hspace{0.05cm}= \hspace{0.05cm}0}=\hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \cdot \big [ {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 \big ]\hspace{0.1cm}{\rm d}x \hspace{0.3cm} + \hspace{0.3cm}\lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \hspace{0.1cm}{\rm d}x \stackrel{!}{=} 0 \hspace{0.05cm}.$$
- This conditional equation can be satisfied independently of $ε_X$ only if holds:
- $${\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 + \lambda = 0 \hspace{0.4cm} \forall x \in \big[-A, +A \big]\hspace{0.3cm} \Rightarrow\hspace{0.3cm} g_X(x) = {\rm const.}\hspace{0.4cm} \forall x \in \big [-A, +A \big]\hspace{0.05cm}.$$
$\text{Summary for peak constraints:}$
The maximum differential entropy is obtained under the constraint $ \vert X \vert ≤ A$ for the »uniform PDF«:
- $$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm A} \cdot A) = {\rm log} \hspace{0.1cm} (2A) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm A} = 2 \hspace{0.05cm}.$$
Any other random variable with the PDF property $f_X(\vert x \vert > A) = 0$ leads to a smaller differential entropy, characterized by the parameter ${\it \Gamma}_{\rm A} < 2$.
Proof: Maximum differential entropy with power constraint
Let's start by explaining the term:
- Actually, it is not the power ⇒ the "second moment" $m_2$ that is limited, but the "second central moment" ⇒ variance $μ_2 = σ^2$.
- We are now looking for the maximum differential entropy under the constraint ${\rm E}\big[|X - m_1|^2 \big] ≤ σ^2$.
- Here we may replace the "smaller/equal sign" by the "equal sign".
If we only allow mean-free random variables, we circumvent the problem. Thus the "Lagrange multiplier":
- $$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} \lambda_1 \cdot \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} \lambda_2 \cdot \int_{-\infty}^{+\infty}\hspace{-0.1cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Following a similar procedure as in the "proof of the peak constraint" it turns out, that the "best possible" function must be $g_X(x) \sim {\rm e}^{–λ_2\hspace{0.05cm} · \hspace{0.05cm} x^2}$ ⇒ "Gaussian distribution":
- $$g_X(x) ={1}/{\sqrt{2\pi \sigma^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{x^2}/{(2 \sigma^2)} }\hspace{0.05cm}.$$
However, we use here for the explicit proof the "Kullback–Leibler distance" between a suitable general PDF $f_X(x)$ and the Gaussian PDF $g_X(x)$:
- $$D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = \int_{-\infty}^{+\infty} \hspace{0.02cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} \frac{f_X(x)}{g_X(x)} \hspace{0.1cm}{\rm d}x = -h(X) - I_2\hspace{0.3cm} \Rightarrow\hspace{0.3cm}I_2 = \int_{-\infty}^{+\infty} \hspace{0.02cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} {g_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
For simplicity, the natural logarithm ⇒ $\ln$ is used here. Thus we obtain for the second integral:
- $$I_2 = - \frac{1}{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{-0.4cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.3cm}- \hspace{0.3cm} \frac{1}{2\sigma^2} \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{0.02cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
By definition, the first integral is equal to $1$ and the second integral gives $σ^2$:
- $$I_2 = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) - {1}/{2} \cdot [{\rm ln} \hspace{0.1cm} ({\rm e})] = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)$$
- $$\Rightarrow\hspace{0.3cm} D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = -h(X) - I_2 = -h(X) + {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$
Since also for continuous random variables the Kullback-Leibler distance is always $\ge 0$ , after generalization ("ln" ⇒ "log"):
- $$h(X) \le {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$
The equal sign only applies if the random variable $X$ is Gaussian distributed.
$\text{Summary for power constraints:}$
The maximum differential entropy is obtained under the condition ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ independent of $m_1$ for the »Gaussian PDF«:
- $$h_{\rm max}(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm} \rm L} \cdot \sigma^2) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm L} = 2\pi{\rm e} \hspace{0.05cm}.$$
Any other continuous random variable $X$ with variance ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ leads to a smaller value, characterized by the parameter ${\it \Gamma}_{\rm L} < 2πe$.
Exercises for the chapter
Exercise 4.1: PDF, CDF and Probability
Exercise 4.1Z: Calculation of Moments
Exercise 4.2Z: Mixed Random Variables
Exercise 4.3: PDF Comparison with Regard to Differential Entropy
Exercise 4.3Z: Exponential and Laplace Distribution
Exercise 4.4: Conventional Entropy and Differential Entropy