Difference between revisions of "Aufgaben:Exercise 3.4Z: GSM Full-Rate Voice Codec"
m (Text replacement - "Mobile_Kommunikation/" to "Mobile_Communications/") |
|||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/Similarities_Between_GSM_and_UMTS |
}} | }} | ||
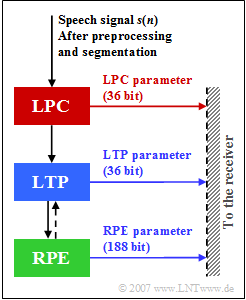
| − | [[File:EN_Mob_A_3_4_Z.png|right|frame|LPC | + | [[File:EN_Mob_A_3_4_Z.png|right|frame|LPC, LTP and RPE parameters in the GSM Full Rate Vocoder]] |
| − | This codec called | + | This codec called "GSM Full Rate Vocoder" (which was standardized for the GSM system in 1991) stands for a joint realization of coder and decoder and combines three methods for the compression of speech signals: |
| − | *Linear Predictive Coding ( | + | *Linear Predictive Coding $\rm (LPC)$, |
| − | |||
| − | |||
| + | *Long Term Prediction $\rm (LTP)$, and | ||
| − | + | *Regular Pulse Excitation $\rm (RPE)$. | |
| − | It should be noted that LTP and RPE, unlike LPC, do not work frame by frame, but with sub-blocks of $5$ milliseconds. However, this has no influence on solving the task. | + | |
| + | The numbers shown in the graphic indicate the number of bits generated by the three units of this Full Rate speech codec per frame of $20$ millisecond duration each. | ||
| + | |||
| + | It should be noted that LTP and RPE, unlike LPC, do not work frame by frame, but with sub-blocks of $5$ milliseconds. However, this has no influence on solving the task. | ||
The input signal in the above graphic is the digitalized speech signal $s_{\rm R}(n)$. | The input signal in the above graphic is the digitalized speech signal $s_{\rm R}(n)$. | ||
This results from the analog speech signal $s(t)$ by | This results from the analog speech signal $s(t)$ by | ||
| − | *a suitable limitation to the bandwidth | + | *a suitable limitation to the bandwidth $B$, |
| − | *sampling at the sampling rate | + | |
| − | + | *sampling at the sampling rate $f_{\rm A} = 8 \ \rm kHz$, | |
| − | |||
| − | + | *quantization with $13 \ \rm bit$, | |
| + | *following segmentation into blocks of each $20 \ \rm ms$. | ||
| + | The further tasks of preprocessing will not be discussed in detail here. | ||
| Line 34: | Line 37: | ||
''Notes:'' | ''Notes:'' | ||
| − | * | + | *The task belongs to the chapter [[Mobile_Communications/Similarities_Between_GSM_and_UMTS|Similarities between GSM and UMTS]]. |
| − | + | *Reference is also made to the Chapter [[Examples_of_Communication_Systems/Voice_Coding|Speech Coding]] of the book "Examples of Communication Systems". | |
| − | *Reference is also made to the Chapter [[ | ||
| Line 45: | Line 47: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {To which bandwidth | + | {To which bandwidth $B$ must the speech signal be limited? |
|type="{}"} | |type="{}"} | ||
$B \ = \ $ { 4 3% } $\ \rm kHz$ | $B \ = \ $ { 4 3% } $\ \rm kHz$ | ||
| − | {Of | + | {Of how many samples $(N_{\rm R})$ is there a speech frame? How large is the input data rate $R_{\rm In}$? |
|type="{}"} | |type="{}"} | ||
$N_{\rm R} \hspace{0.18cm} = \ $ { 160 3% } $\ \rm samples$ | $N_{\rm R} \hspace{0.18cm} = \ $ { 160 3% } $\ \rm samples$ | ||
$R_{\rm In} \hspace{0.15cm} = \ $ { 104 3% } $\ \rm kbit/s$ | $R_{\rm In} \hspace{0.15cm} = \ $ { 104 3% } $\ \rm kbit/s$ | ||
| − | {What is the output data rate | + | {What is the output data rate $R_{\rm Out}$ of the GSM–full rate codec? |
|type="{}"} | |type="{}"} | ||
$R_{\rm Out} \ = \ $ { 13 3% } $\ \rm kbit/s$ | $R_{\rm Out} \ = \ $ { 13 3% } $\ \rm kbit/s$ | ||
| Line 64: | Line 66: | ||
+ The $36$ LPC bits specify coefficients that the receiver uses to undo the LPC filtering. | + The $36$ LPC bits specify coefficients that the receiver uses to undo the LPC filtering. | ||
- The filter for short-term prediction is recursive. | - The filter for short-term prediction is recursive. | ||
| − | - The LPC output signal is identical to the input $s_{\rm R}(t)$. | + | - The LPC output signal is identical to the input signal $s_{\rm R}(t)$. |
| − | {Which statements regarding the block | + | {Which statements regarding the block "LTP" are true? |
|type="[]"} | |type="[]"} | ||
+ LTP removes periodic structures of the speech signal. | + LTP removes periodic structures of the speech signal. | ||
| Line 77: | Line 79: | ||
+ RPE removes unimportant parts for the subjective impression. | + RPE removes unimportant parts for the subjective impression. | ||
+ RPE subdivides each sub-block into four sub-sequences. | + RPE subdivides each sub-block into four sub-sequences. | ||
| − | - RPE selects the | + | - RPE selects the sub-sequence with the minimum energy. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' To satisfy the sampling theorem, the bandwidth $B$ must not exceed $ f_{\rm A}/2 \hspace{0.15cm}\underline{= 4 \ \ \rm kHz}$. | + | '''(1)''' To satisfy the sampling theorem, the bandwidth $B$ must not exceed $ f_{\rm A}/2 \hspace{0.15cm}\underline{= 4 \ \ \rm kHz}$. |
| − | '''(2)''' The given sampling rate $f_{\rm A} = 8 \ \rm kHz$ results in a distance between individual samples of $T_{\rm A} = 0.125 \ \rm ms$. | + | '''(2)''' The given sampling rate $f_{\rm A} = 8 \ \rm kHz$ results in a distance between individual samples of $T_{\rm A} = 0.125 \ \rm ms$. |
| − | *Thus a speech frame of $ | + | *Thus a speech frame of $20 {\rm ms}$ consists of $N_{\rm R} = 20/0.125 = \underline{160 \ \rm samples}$, each quantized with $13 \ \rm bit$. |
*The data rate is thus | *The data rate is thus | ||
:$$R_{\rm In} = \frac{160 \cdot 13}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 104\,{\rm kbit/s}}\hspace{0.05cm}.$$ | :$$R_{\rm In} = \frac{160 \cdot 13}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 104\,{\rm kbit/s}}\hspace{0.05cm}.$$ | ||
| Line 95: | Line 97: | ||
| − | '''(3)''' The graph shows that per speech frame $36 \ {\rm (LPC)} + 36 \ {\rm (LTP)} + 188 \ {\rm (RPE)} = 260 \ \ \rm | + | '''(3)''' The graph shows that per speech frame $36 \ {\rm (LPC)} + 36 \ {\rm (LTP)} + 188 \ {\rm (RPE)} = 260 \ \ \rm bit$ are output. |
*From this the output data rate is calculated as | *From this the output data rate is calculated as | ||
:$$R_{\rm Out} = \frac{260}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 13\,{\rm kbit/s}}\hspace{0.05cm}.$$ | :$$R_{\rm Out} = \frac{260}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 13\,{\rm kbit/s}}\hspace{0.05cm}.$$ | ||
| − | *The compression factor achieved by the full rate speech codec is thus $104/13 = $ | + | *The compression factor achieved by the full rate speech codec is thus $104/13 = 8$. |
| − | '''(4)''' | + | '''(4)''' The <u>first two statements</u> are true: |
| − | *The 36 LPC | + | *The 36 LPC bits describe a total of eight filter coefficients of a non-recursive filter, whereby eight $\rm ACF$ values are determined from the short-term analysis and where these are converted into reflection factors $r_{k}$ after the so-called "Schur recursion". |
| − | *From these the eight LAR | + | *From these the eight LAR coefficients are calculated according to the function ${\rm ln}\big[(1 - r_{k})/(1 + r_{k})\big]$, quantized with a different number of bits and sent to the receiver. |
| − | *The LPC output signal has a significantly lower amplitude than its input $s_{\rm R}(n)$, and it has a significantly reduced dynamic range and a flatter spectrum. | + | *The LPC output signal has a significantly lower amplitude than its input $s_{\rm R}(n)$, and it has a significantly reduced dynamic range and a flatter spectrum. |
| − | '''(5)''' Correct are the <u> | + | '''(5)''' Correct are the <u>statements 1 and 3</u>, but not the second: |
| − | *The LTP | + | *The LTP analysis and filtering is done blockwise every $5 \ \rm ms$ ⇒ $(40$ samples$)$, i.e. four times per speech frame. |
| − | *The cross correlation function (CCF) between the current sub-block and the three previous sub-blocks is formed. | + | *The cross correlation function $\rm (CCF)$ between the current sub-block and the three previous sub-blocks is formed. |
| − | *For each sub-block, an LTP | + | *For each sub-block, an LTP delay and an LTP gain are determined which best match the sub-block. |
| − | *A correction signal of the following component | + | *A correction signal of the following component "RPE" is also taken into account. |
*For the long-term prediction, as with the LPC, the output is reduced in redundancy compared to the input. | *For the long-term prediction, as with the LPC, the output is reduced in redundancy compared to the input. | ||
| Line 119: | Line 121: | ||
'''(6)''' The statements <u>2 and 3</u> are correct: | '''(6)''' The statements <u>2 and 3</u> are correct: | ||
| − | *The fact that statement 1 is wrong can be seen from the graphic on the data page, because $188$ of the $260$ output bits come from the RPE. | + | *The fact that statement 1 is wrong can be seen from the graphic on the data page, because $188$ of the $260$ output bits come from the RPE. Voice would be understandable with RPE alone (without LPC and LTP). |
| − | *Regarding the last statement: The RPE is of course looking for the subsequence with the '''maximum'' energy. The RPE pulses are a subsequence (13 of 40 samples) of three bits per subframe of $5 \ \rm ms$ and accordingly $12 | + | *Regarding the last statement: The RPE is of course looking for the subsequence with the '''maximum''' energy. The RPE pulses are a subsequence $(13$ of $40$ samples$)$ of three bits per subframe of $5 \ \rm ms$ and accordingly $12$ bits per $20 \ \rm ms$ frame. |
| − | *The "RPE pulse" thus occupies $13 \cdot 12 = 156$ of the $260$ output bits. | + | *The "RPE pulse" thus occupies $13 \cdot 12 = 156$ of the $260$ output bits. |
| − | More details about the RPE block can be found on the page [[ | + | More details about the RPE block can be found on the page [[Examples_of_Communication_Systems/Voice_Coding#Regular_Pulse_Excitation_.E2.80.93_RPE_Coding|RPE coding]] of the book "Examples of Communication Systems". |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 130: | Line 132: | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^3.2 Similarities between GSM and UMTS |
^]] | ^]] | ||
Latest revision as of 12:25, 23 January 2023
This codec called "GSM Full Rate Vocoder" (which was standardized for the GSM system in 1991) stands for a joint realization of coder and decoder and combines three methods for the compression of speech signals:
- Linear Predictive Coding $\rm (LPC)$,
- Long Term Prediction $\rm (LTP)$, and
- Regular Pulse Excitation $\rm (RPE)$.
The numbers shown in the graphic indicate the number of bits generated by the three units of this Full Rate speech codec per frame of $20$ millisecond duration each.
It should be noted that LTP and RPE, unlike LPC, do not work frame by frame, but with sub-blocks of $5$ milliseconds. However, this has no influence on solving the task.
The input signal in the above graphic is the digitalized speech signal $s_{\rm R}(n)$.
This results from the analog speech signal $s(t)$ by
- a suitable limitation to the bandwidth $B$,
- sampling at the sampling rate $f_{\rm A} = 8 \ \rm kHz$,
- quantization with $13 \ \rm bit$,
- following segmentation into blocks of each $20 \ \rm ms$.
The further tasks of preprocessing will not be discussed in detail here.
Notes:
- The task belongs to the chapter Similarities between GSM and UMTS.
- Reference is also made to the Chapter Speech Coding of the book "Examples of Communication Systems".
Questionnaire
Solution
(1) To satisfy the sampling theorem, the bandwidth $B$ must not exceed $ f_{\rm A}/2 \hspace{0.15cm}\underline{= 4 \ \ \rm kHz}$.
(2) The given sampling rate $f_{\rm A} = 8 \ \rm kHz$ results in a distance between individual samples of $T_{\rm A} = 0.125 \ \rm ms$.
- Thus a speech frame of $20 {\rm ms}$ consists of $N_{\rm R} = 20/0.125 = \underline{160 \ \rm samples}$, each quantized with $13 \ \rm bit$.
- The data rate is thus
- $$R_{\rm In} = \frac{160 \cdot 13}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 104\,{\rm kbit/s}}\hspace{0.05cm}.$$
(3) The graph shows that per speech frame $36 \ {\rm (LPC)} + 36 \ {\rm (LTP)} + 188 \ {\rm (RPE)} = 260 \ \ \rm bit$ are output.
- From this the output data rate is calculated as
- $$R_{\rm Out} = \frac{260}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 13\,{\rm kbit/s}}\hspace{0.05cm}.$$
- The compression factor achieved by the full rate speech codec is thus $104/13 = 8$.
(4) The first two statements are true:
- The 36 LPC bits describe a total of eight filter coefficients of a non-recursive filter, whereby eight $\rm ACF$ values are determined from the short-term analysis and where these are converted into reflection factors $r_{k}$ after the so-called "Schur recursion".
- From these the eight LAR coefficients are calculated according to the function ${\rm ln}\big[(1 - r_{k})/(1 + r_{k})\big]$, quantized with a different number of bits and sent to the receiver.
- The LPC output signal has a significantly lower amplitude than its input $s_{\rm R}(n)$, and it has a significantly reduced dynamic range and a flatter spectrum.
(5) Correct are the statements 1 and 3, but not the second:
- The LTP analysis and filtering is done blockwise every $5 \ \rm ms$ ⇒ $(40$ samples$)$, i.e. four times per speech frame.
- The cross correlation function $\rm (CCF)$ between the current sub-block and the three previous sub-blocks is formed.
- For each sub-block, an LTP delay and an LTP gain are determined which best match the sub-block.
- A correction signal of the following component "RPE" is also taken into account.
- For the long-term prediction, as with the LPC, the output is reduced in redundancy compared to the input.
(6) The statements 2 and 3 are correct:
- The fact that statement 1 is wrong can be seen from the graphic on the data page, because $188$ of the $260$ output bits come from the RPE. Voice would be understandable with RPE alone (without LPC and LTP).
- Regarding the last statement: The RPE is of course looking for the subsequence with the maximum energy. The RPE pulses are a subsequence $(13$ of $40$ samples$)$ of three bits per subframe of $5 \ \rm ms$ and accordingly $12$ bits per $20 \ \rm ms$ frame.
- The "RPE pulse" thus occupies $13 \cdot 12 = 156$ of the $260$ output bits.
More details about the RPE block can be found on the page RPE coding of the book "Examples of Communication Systems".