Difference between revisions of "Aufgaben:Exercise 3.7: PN Modulation"
From LNTwww
m (Text replacement - "transmit signal" to "transmitted signal") |
m (Text replacement - "Category:Exercises for Mobile Communications" to "Category:Mobile Communications: Exercises") |
||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/Characteristics_of_UMTS |
}} | }} | ||
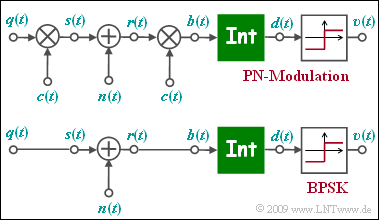
| − | [[File:P_ID2259__Mod_Z_5_2.png|right|frame|Equivalent | + | [[File:P_ID2259__Mod_Z_5_2.png|right|frame|Equivalent models for "PN modulation" and "BPSK"]] |
| − | The | + | The figure shows the equivalent block diagram of "PN modulation" or "Direct Sequence Spread Spectrum", abbreviated $\rm DS-SS$ in the equivalent low-pass range, where $n(t)$ stands for AWGN noise. |
| − | Below, the low-pass model of binary phase modulation (BPSK) is sketched | + | Below, the low-pass model of binary phase modulation $\rm (BPSK)$ is sketched. |
| − | *The low-pass | + | *The low-pass transmission signal $s(t)$ is equal to the rectangular source signal $q(t) ∈ \{+1, -1\}$ with rectangular duration $T$ only for reasons of uniformity. |
*The function of the integrator can be written as follows: | *The function of the integrator can be written as follows: | ||
:$$d (\nu T) = \frac{1}{T} \cdot \int_{(\nu -1 )T }^{\nu T} \hspace{-0.03cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$ | :$$d (\nu T) = \frac{1}{T} \cdot \int_{(\nu -1 )T }^{\nu T} \hspace{-0.03cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$ | ||
| − | *The two models differ in the multiplication by the $±1$ | + | *The two models differ in the multiplication by the $±1$ spreading signal $c(t)$ at the transmitter and the receiver. Of the signal $c(t)$ only the spread degree $J$ is known. |
| − | *The specification of the specific spreading sequence (M sequence or Walsh function) is not important for the solution of this task. | + | *The specification of the specific spreading sequence $($"M sequence" or "Walsh function"$)$ is not important for the solution of this task. |
| − | It has to be examined whether the lower BPSK model can also be applied with PN modulation and whether the BPSK error probability | + | It has to be examined whether the lower BPSK model can also be applied with "PN modulation" and whether the BPSK error probability |
:$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$ | :$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$ | ||
| − | is also valid for PN modulation, or how the | + | is also valid for "PN modulation", or how the given equation should be modified. |
| Line 26: | Line 26: | ||
''Notes:'' | ''Notes:'' | ||
| − | *This | + | *This task refers to the chapter [[Mobile_Communications/Characteristics_of_UMTS|Characteristics of UMTS]]. |
| − | |||
*The CDMA method used for UMTS is also known as "PN modulation". | *The CDMA method used for UMTS is also known as "PN modulation". | ||
| − | *The nomenclature used in this task is | + | *The nomenclature used in this task is partly based on the page [[Modulation_Methods/Direct-Sequence_Spread_Spectrum_Modulation|Direct-sequence spread spectrum modulation]] of the book "Modulation Methods". |
| Line 35: | Line 34: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Which detection | + | {Which values for the detection signal $d(t)$ are possible with BPSK (without noise)? |
|type="[]"} | |type="[]"} | ||
| − | - $d(\nu T)$ is | + | - $d(\nu T)$ is Gaussian distributed. |
| − | - $d(\nu T)$ can take the values $+1$, $0$ | + | - $d(\nu T)$ can take the values $+1$, $0$ and $-1$ . |
| − | + Only the values $d(\nu T) = +1$ | + | + Only the values $d(\nu T) = +1$ and $d(\nu T) = -1$ are possible. |
| − | {Which values are possible with PN modulation in a noise-free case | + | {Which values are possible with PN modulation in a noise-free case? |
|type="[]"} | |type="[]"} | ||
| − | - $d(\nu T)$ is | + | - $d(\nu T)$ is Gaussian distributed. |
- $d(\nu T)$ can take the values $+1$, $0$ und $-1$ . | - $d(\nu T)$ can take the values $+1$, $0$ und $-1$ . | ||
+ Only the values $d(\nu T) = +1$ und $d(\nu T) = -1$ are possible. | + Only the values $d(\nu T) = +1$ und $d(\nu T) = -1$ are possible. | ||
| − | {What modification must be | + | {What modification must be done to the BPSK model so that it can also be used for PN modulation? |
|type="[]"} | |type="[]"} | ||
| − | + The noise $n(t)$ must be replaced by $n\hspace{0.05cm}'(t) = n(t) \cdot c(t)$ | + | + The noise $n(t)$ must be replaced by $n\hspace{0.05cm}'(t) = n(t) \cdot c(t)$. |
| − | - The integration must now be done via $J \cdot T$ | + | - The integration must now be done via $J \cdot T$. |
- The noise power must be reduced by the factor $J$ . | - The noise power must be reduced by the factor $J$ . | ||
| − | {The following applies $10 \cdot {\rm lg}\ (E_{\rm B}/N_0) = 6 \ \rm dB$. | + | {The following applies $10 \cdot {\rm lg}\ (E_{\rm B}/N_0) = 6 \ \rm dB$. What error probability $p_{\rm B}$ results with PN modulation? <br>''Hint'': For BPSK, the result is $p_{\rm B} \approx 2.3 \cdot 10^{-3}$. |
|type="[]"} | |type="[]"} | ||
| − | - The larger $J$ is selected, the smaller $p_{\rm B}$ is. | + | - The larger $J$ is selected, the smaller $p_{\rm B}$ is. |
| − | - The larger $J$ is selected, the larger $p_{\rm B}$. | + | - The larger $J$ is selected, the larger $p_{\rm B}$. |
| − | + It results | + | + It results always the value $p_{\rm B} = 2.3 \cdot 10^{-3}$ results, independently from $J$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Correct is the <u>solution 3</u>: | '''(1)''' Correct is the <u>solution 3</u>: | ||
| − | *This is an optimal receiver. | + | *This is an optimal receiver. |
| − | *Without noise, the signal $b(t)$ | + | *Without noise, the signal $b(t)$ is constantly equal to $+1$ or $-1$ within each bit. |
*From the equation given for the integrator | *From the equation given for the integrator | ||
:$$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.03cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t$$ | :$$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.03cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t$$ | ||
| − | :follows that $d(\nu T)$ can only take the values $±1$. | + | :follows that $d(\nu T)$ can only take the values $±1$. |
| − | '''(2)''' | + | '''(2)''' Correct is the <u>solution 3</u>. |
| − | * | + | *In the noise-free case ⇒ $n(t) = 0$, the twofold multiplication by $c(t) ∈ \{+1, -1\}$ ⇒ $c(t)^{2} = 1$ can be omitted, |
| + | *so that the upper model is identical to the lower model. | ||
'''(3)''' The <u>solution 1</u> is applicable: | '''(3)''' The <u>solution 1</u> is applicable: | ||
| − | *Since both models are identical in the noiseless case, only the noise signal has to be adjusted: $n'(t) = n(t) \cdot c(t)$. | + | *Since both models are identical in the noiseless case, only the noise signal has to be adjusted: $n'(t) = n(t) \cdot c(t)$. |
| − | *The solutions 2 and 3 | + | *The solutions 2 and 3 are not applicable: Integration must still be done via $T = J \cdot T_{c}$ $($not via $J \cdot T)$ and PN modulation does not reduce the AWGN noise. |
| − | '''(4)''' | + | '''(4)''' Correct is the <u>solution 3</u>: |
| − | *The equation valid for BPSK and AWGN channel | + | *The equation valid for BPSK and AWGN channel is also applicable to PN modulation, independent of the spreading factor $J$ and the specific spreading sequence: |
| − | :$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { | + | :$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$ |
| − | |||
*For AWGN noise, the error probability is neither increased nor decreased by band spreading. | *For AWGN noise, the error probability is neither increased nor decreased by band spreading. | ||
| Line 91: | Line 90: | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^3.4 Characteristics of UMTS^]] |
Latest revision as of 13:38, 23 March 2021
The figure shows the equivalent block diagram of "PN modulation" or "Direct Sequence Spread Spectrum", abbreviated $\rm DS-SS$ in the equivalent low-pass range, where $n(t)$ stands for AWGN noise. Below, the low-pass model of binary phase modulation $\rm (BPSK)$ is sketched.
- The low-pass transmission signal $s(t)$ is equal to the rectangular source signal $q(t) ∈ \{+1, -1\}$ with rectangular duration $T$ only for reasons of uniformity.
- The function of the integrator can be written as follows:
- $$d (\nu T) = \frac{1}{T} \cdot \int_{(\nu -1 )T }^{\nu T} \hspace{-0.03cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$
- The two models differ in the multiplication by the $±1$ spreading signal $c(t)$ at the transmitter and the receiver. Of the signal $c(t)$ only the spread degree $J$ is known.
- The specification of the specific spreading sequence $($"M sequence" or "Walsh function"$)$ is not important for the solution of this task.
It has to be examined whether the lower BPSK model can also be applied with "PN modulation" and whether the BPSK error probability
- $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$
is also valid for "PN modulation", or how the given equation should be modified.
Notes:
- This task refers to the chapter Characteristics of UMTS.
- The CDMA method used for UMTS is also known as "PN modulation".
- The nomenclature used in this task is partly based on the page Direct-sequence spread spectrum modulation of the book "Modulation Methods".
Questionnaire
Solution
(1) Correct is the solution 3:
- This is an optimal receiver.
- Without noise, the signal $b(t)$ is constantly equal to $+1$ or $-1$ within each bit.
- From the equation given for the integrator
- $$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.03cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t$$
- follows that $d(\nu T)$ can only take the values $±1$.
(2) Correct is the solution 3.
- In the noise-free case ⇒ $n(t) = 0$, the twofold multiplication by $c(t) ∈ \{+1, -1\}$ ⇒ $c(t)^{2} = 1$ can be omitted,
- so that the upper model is identical to the lower model.
(3) The solution 1 is applicable:
- Since both models are identical in the noiseless case, only the noise signal has to be adjusted: $n'(t) = n(t) \cdot c(t)$.
- The solutions 2 and 3 are not applicable: Integration must still be done via $T = J \cdot T_{c}$ $($not via $J \cdot T)$ and PN modulation does not reduce the AWGN noise.
(4) Correct is the solution 3:
- The equation valid for BPSK and AWGN channel is also applicable to PN modulation, independent of the spreading factor $J$ and the specific spreading sequence:
- $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$
- For AWGN noise, the error probability is neither increased nor decreased by band spreading.