Difference between revisions of "Aufgaben:Exercise 3.4Z: GSM Full-Rate Voice Codec"
m (Text replacement - "Category:Exercises for Mobile Communications" to "Category:Mobile Communications: Exercises") |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 5: | Line 5: | ||
}} | }} | ||
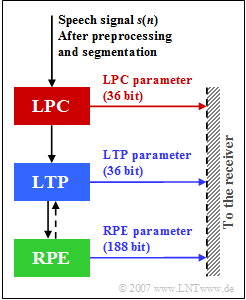
| − | [[File:EN_Mob_A_3_4_Z.png|right|frame|LPC, LTP and RPE parameters in the GSM Full | + | [[File:EN_Mob_A_3_4_Z.png|right|frame|LPC, LTP and RPE parameters in the GSM Full Rate Vocoder]] |
| − | This codec called "GSM Full | + | This codec called "GSM Full Rate Vocoder" (which was standardized for the GSM system in 1991) stands for a joint realization of coder and decoder and combines three methods for the compression of speech signals: |
*Linear Predictive Coding $\rm (LPC)$, | *Linear Predictive Coding $\rm (LPC)$, | ||
| + | |||
*Long Term Prediction $\rm (LTP)$, and | *Long Term Prediction $\rm (LTP)$, and | ||
| + | |||
*Regular Pulse Excitation $\rm (RPE)$. | *Regular Pulse Excitation $\rm (RPE)$. | ||
| − | The numbers shown in the graphic indicate the number of bits generated by the three units of this Full | + | The numbers shown in the graphic indicate the number of bits generated by the three units of this Full Rate speech codec per frame of $20$ millisecond duration each. |
It should be noted that LTP and RPE, unlike LPC, do not work frame by frame, but with sub-blocks of $5$ milliseconds. However, this has no influence on solving the task. | It should be noted that LTP and RPE, unlike LPC, do not work frame by frame, but with sub-blocks of $5$ milliseconds. However, this has no influence on solving the task. | ||
| Line 20: | Line 22: | ||
This results from the analog speech signal $s(t)$ by | This results from the analog speech signal $s(t)$ by | ||
*a suitable limitation to the bandwidth $B$, | *a suitable limitation to the bandwidth $B$, | ||
| + | |||
*sampling at the sampling rate $f_{\rm A} = 8 \ \rm kHz$, | *sampling at the sampling rate $f_{\rm A} = 8 \ \rm kHz$, | ||
| + | |||
*quantization with $13 \ \rm bit$, | *quantization with $13 \ \rm bit$, | ||
| + | |||
*following segmentation into blocks of each $20 \ \rm ms$. | *following segmentation into blocks of each $20 \ \rm ms$. | ||
| Line 33: | Line 38: | ||
*The task belongs to the chapter [[Mobile_Communications/Similarities_Between_GSM_and_UMTS|Similarities between GSM and UMTS]]. | *The task belongs to the chapter [[Mobile_Communications/Similarities_Between_GSM_and_UMTS|Similarities between GSM and UMTS]]. | ||
| − | *Reference is also made to the Chapter [[Examples_of_Communication_Systems/Voice_Coding| | + | *Reference is also made to the Chapter [[Examples_of_Communication_Systems/Voice_Coding|Speech Coding]] of the book "Examples of Communication Systems". |
| Line 95: | Line 100: | ||
*From this the output data rate is calculated as | *From this the output data rate is calculated as | ||
:$$R_{\rm Out} = \frac{260}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 13\,{\rm kbit/s}}\hspace{0.05cm}.$$ | :$$R_{\rm Out} = \frac{260}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 13\,{\rm kbit/s}}\hspace{0.05cm}.$$ | ||
| − | *The compression factor achieved by the full | + | *The compression factor achieved by the full rate speech codec is thus $104/13 = 8$. |
Latest revision as of 12:25, 23 January 2023
This codec called "GSM Full Rate Vocoder" (which was standardized for the GSM system in 1991) stands for a joint realization of coder and decoder and combines three methods for the compression of speech signals:
- Linear Predictive Coding $\rm (LPC)$,
- Long Term Prediction $\rm (LTP)$, and
- Regular Pulse Excitation $\rm (RPE)$.
The numbers shown in the graphic indicate the number of bits generated by the three units of this Full Rate speech codec per frame of $20$ millisecond duration each.
It should be noted that LTP and RPE, unlike LPC, do not work frame by frame, but with sub-blocks of $5$ milliseconds. However, this has no influence on solving the task.
The input signal in the above graphic is the digitalized speech signal $s_{\rm R}(n)$.
This results from the analog speech signal $s(t)$ by
- a suitable limitation to the bandwidth $B$,
- sampling at the sampling rate $f_{\rm A} = 8 \ \rm kHz$,
- quantization with $13 \ \rm bit$,
- following segmentation into blocks of each $20 \ \rm ms$.
The further tasks of preprocessing will not be discussed in detail here.
Notes:
- The task belongs to the chapter Similarities between GSM and UMTS.
- Reference is also made to the Chapter Speech Coding of the book "Examples of Communication Systems".
Questionnaire
Solution
(1) To satisfy the sampling theorem, the bandwidth $B$ must not exceed $ f_{\rm A}/2 \hspace{0.15cm}\underline{= 4 \ \ \rm kHz}$.
(2) The given sampling rate $f_{\rm A} = 8 \ \rm kHz$ results in a distance between individual samples of $T_{\rm A} = 0.125 \ \rm ms$.
- Thus a speech frame of $20 {\rm ms}$ consists of $N_{\rm R} = 20/0.125 = \underline{160 \ \rm samples}$, each quantized with $13 \ \rm bit$.
- The data rate is thus
- $$R_{\rm In} = \frac{160 \cdot 13}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 104\,{\rm kbit/s}}\hspace{0.05cm}.$$
(3) The graph shows that per speech frame $36 \ {\rm (LPC)} + 36 \ {\rm (LTP)} + 188 \ {\rm (RPE)} = 260 \ \ \rm bit$ are output.
- From this the output data rate is calculated as
- $$R_{\rm Out} = \frac{260}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 13\,{\rm kbit/s}}\hspace{0.05cm}.$$
- The compression factor achieved by the full rate speech codec is thus $104/13 = 8$.
(4) The first two statements are true:
- The 36 LPC bits describe a total of eight filter coefficients of a non-recursive filter, whereby eight $\rm ACF$ values are determined from the short-term analysis and where these are converted into reflection factors $r_{k}$ after the so-called "Schur recursion".
- From these the eight LAR coefficients are calculated according to the function ${\rm ln}\big[(1 - r_{k})/(1 + r_{k})\big]$, quantized with a different number of bits and sent to the receiver.
- The LPC output signal has a significantly lower amplitude than its input $s_{\rm R}(n)$, and it has a significantly reduced dynamic range and a flatter spectrum.
(5) Correct are the statements 1 and 3, but not the second:
- The LTP analysis and filtering is done blockwise every $5 \ \rm ms$ ⇒ $(40$ samples$)$, i.e. four times per speech frame.
- The cross correlation function $\rm (CCF)$ between the current sub-block and the three previous sub-blocks is formed.
- For each sub-block, an LTP delay and an LTP gain are determined which best match the sub-block.
- A correction signal of the following component "RPE" is also taken into account.
- For the long-term prediction, as with the LPC, the output is reduced in redundancy compared to the input.
(6) The statements 2 and 3 are correct:
- The fact that statement 1 is wrong can be seen from the graphic on the data page, because $188$ of the $260$ output bits come from the RPE. Voice would be understandable with RPE alone (without LPC and LTP).
- Regarding the last statement: The RPE is of course looking for the subsequence with the maximum energy. The RPE pulses are a subsequence $(13$ of $40$ samples$)$ of three bits per subframe of $5 \ \rm ms$ and accordingly $12$ bits per $20 \ \rm ms$ frame.
- The "RPE pulse" thus occupies $13 \cdot 12 = 156$ of the $260$ output bits.
More details about the RPE block can be found on the page RPE coding of the book "Examples of Communication Systems".