Difference between revisions of "Aufgaben:Exercise 2.4: About the LZW Algorithm"
| (7 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Compression_According_to_Lempel,_Ziv_and_Welch |
}} | }} | ||
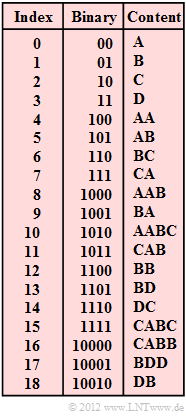
| − | [[File:EN_Inf_A_2_4.png|right|frame|LZW | + | [[File:EN_Inf_A_2_4.png|right|frame|LZW dictionary for Encoding/Decoding]] |
| − | The compression algorithm "LZW " – named after the inventors [https://en.wikipedia.org/wiki/Abraham_Lempel Abraham Lempel], [https://en.wikipedia.org/wiki/Jacob_Ziv Jacob Ziv] and [https://en.wikipedia.org/wiki/Terry_Welch Terry Welch] – works like "LZ78 " with a global dictionary. In this case, all possible characters – in the example <b>A</b>, <b>B</b>, <b>C</b>, <b>D</b> – are preassigned at the beginning and are successively expanded during encoding. | + | The compression algorithm "LZW" – named after the inventors [https://en.wikipedia.org/wiki/Abraham_Lempel Abraham Lempel], [https://en.wikipedia.org/wiki/Jacob_Ziv Jacob Ziv] and [https://en.wikipedia.org/wiki/Terry_Welch Terry Welch] – works like "LZ78" with a global dictionary. In this case, all possible characters – in the example <b>A</b>, <b>B</b>, <b>C</b>, <b>D</b> – are preassigned at the beginning and are successively expanded during encoding. |
| − | During decoding, exactly the same dictionary is created, only the same entry with index $I$ is made one step later than during | + | During decoding, exactly the same dictionary is created, only the same entry with index $I$ is made one step later than during encoding. To designate the decoding steps, we use the variable $i$. |
Here are some more notes on LZW encoding and decoding: | Here are some more notes on LZW encoding and decoding: | ||
| − | *During encoding, at each time $i$ | + | *During encoding, at each time $i$, a search is made in the dictionary for the longest possible character string that matches the input string currently present. |
*The dictionary index $I_i$ found is always transmitted in binary form. At the same time, $W(I_i) + Z$ is entered into the dictionary under the next free index. | *The dictionary index $I_i$ found is always transmitted in binary form. At the same time, $W(I_i) + Z$ is entered into the dictionary under the next free index. | ||
*Here, $W(I_i)$ denotes a character or a character string, and $Z$ is the first character of the upcoming input string (i.e. also a character), which is no longer considered in $W(I_i)$ . | *Here, $W(I_i)$ denotes a character or a character string, and $Z$ is the first character of the upcoming input string (i.e. also a character), which is no longer considered in $W(I_i)$ . | ||
| − | *With $M = 4$ possible characters, the first index $I_1$ is transmitted with two bits, the indices $I_2$, ... , $I_5$ with three bits, the next eight indices with four bits, then 16 indices with five bits, etc. The reason for this bit-saving measure can be found in the | + | *With $M = 4$ possible characters, the first index $I_1$ is transmitted with two bits, the indices $I_2$, ... , $I_5$ with three bits, the next eight indices with four bits, then 16 indices with five bits, etc. The reason for this bit-saving measure can be found in the solution to this task. |
| − | After coding in the manner described here over $16$ coding steps, the following binary sequence of length $N_{\rm | + | After coding in the manner described here over $16$ coding steps, the following binary sequence of length $N_{\rm bit} = 61$: |
:$$\boldsymbol{\rm 00 \ 000 \ 001 \ 010 \ 100 \ 0001 \ 1000 \ 0111 \ 0001 \ 0001 \ 0011 \ 1011 \ 1011 \ 01101 \ 00011 \ 01001}\hspace{0.05cm}.$$ | :$$\boldsymbol{\rm 00 \ 000 \ 001 \ 010 \ 100 \ 0001 \ 1000 \ 0111 \ 0001 \ 0001 \ 0011 \ 1011 \ 1011 \ 01101 \ 00011 \ 01001}\hspace{0.05cm}.$$ | ||
| Line 29: | Line 29: | ||
| − | + | Hints: | |
| − | *The | + | *The exercise belongs to the chapter [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch|Compression according to Lempel, Ziv and Welch]]. |
| − | * | + | *In particular, reference is made to the pages |
:: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#LZ77_-_the_basic_form_of_the_Lempel-Ziv_algorithms|LZ77 - the basic form of Lempel-Ziv algorithms]], | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#LZ77_-_the_basic_form_of_the_Lempel-Ziv_algorithms|LZ77 - the basic form of Lempel-Ziv algorithms]], | ||
:: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Lempel-Ziv_coding_with_variable_index_bit_length|Lempel-Ziv coding with variable index bit length]], | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Lempel-Ziv_coding_with_variable_index_bit_length|Lempel-Ziv coding with variable index bit length]], | ||
| − | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Decoding_of_the_LZW_algorithm| | + | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Decoding_of_the_LZW_algorithm|Decoding of the LZW algorithm]]. |
| − | * [[Aufgaben: | + | * [[Aufgaben:Exercise_2.3:_About_the_LZ78_Compression|Exercise 2.3]] and [[Aufgaben:Exercise_2.3Z:_About_the_LZ77_Coding|Exercise 2.3Z]] deal with other Lempel-Ziv methods in a similar way. |
| Line 43: | Line 43: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Which indices are available for the first four steps $i=1$, ... , $i=4$ for decoding Enter all $I_i = I(i)$ as decimal numbers. | + | {Which indices are available for the first four steps $(i=1$, ... , $i=4)$ for decoding. Enter all $I_i = I(i)$ as decimal numbers. |
|type="{}"} | |type="{}"} | ||
$I_1 \ = \ $ { 0. } | $I_1 \ = \ $ { 0. } | ||
| Line 69: | Line 69: | ||
{The next index is: $I_{17} = 10010$ (binary) $= 18$ (decimal). Which of the following statements are true? | {The next index is: $I_{17} = 10010$ (binary) $= 18$ (decimal). Which of the following statements are true? | ||
|type="[]"} | |type="[]"} | ||
| − | + The decoder output to step $i = 17$ | + | + The decoder output to step $i = 17$ is "<b>DB</b>". |
| − | - The decoder output to step $i = 17$ | + | - The decoder output to step $i = 17$ is "<b>BAD</b>". |
| − | - New dictionary entry <b>DB</b> in line $I = 19$. | + | - New dictionary entry "<b>DB</b>" in line $I = 19$. |
| − | + New dictionary entry <b>BAD</b> in line $I = 19$. | + | + New dictionary entry "<b>BAD</b>" in line $I = 19$. |
| − | {Let the decoder input string consist of $N_{\rm | + | {Let the decoder input string consist of $N_{\rm bit} = 300$ binary characters (bits). Which of the following statements is then certainly true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $58$ LZW phrases with variable bit length were transmitted. |
- With a uniform index bit length, fewer bits would be required. | - With a uniform index bit length, fewer bits would be required. | ||
- A file with $N =150$ quaternary characters was transmitted. | - A file with $N =150$ quaternary characters was transmitted. | ||
| Line 87: | Line 87: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' For the LZW coding of the first character $(i = 1)$ | + | '''(1)''' For the LZW coding of the first character $(i = 1)$, only the four indices $I = 0$, ... , $I = 3$ are possible for which a dictionary entry has already been made at step $i = 0$ (preassignment). Therefore, it is sufficient here to transmit the index with two bits. |
| − | *In contrast, three bits are already required for step $i = 2$ | + | *In contrast, three bits are already required for step $i = 2$. If the input sequence had started with <b>AAA</b> , the LZW coding $I_2 = I(i = 2)$ would have resulted in the decimal value $4$. This can no longer be represented with two bits and must be coded with three bits, just like $I_3$, $I_4$ and $I_5$. |
*The given input string:$$\boldsymbol{\rm 00 000 001 010 100 0001}\hspace{0.05cm}...$$ | *The given input string:$$\boldsymbol{\rm 00 000 001 010 100 0001}\hspace{0.05cm}...$$ | ||
:must therefore be divided by the decoder as follows: | :must therefore be divided by the decoder as follows: | ||
| − | :$$\boldsymbol{\rm 00 | 000 |001 |010 |100 |0001|}\hspace{0.05cm}...$$ | + | :$$\boldsymbol{\rm 00 |000 |001 |010 |100 |0001|}\hspace{0.05cm}...$$ |
*The decoder results of the first four steps are therefore: | *The decoder results of the first four steps are therefore: | ||
| Line 104: | Line 104: | ||
'''(2)''' If one takes into account that | '''(2)''' If one takes into account that | ||
* for $i = 1$ two bits are used, | * for $i = 1$ two bits are used, | ||
| − | * for $2 ≤ i ≤ 5$ three bits, | + | * for $2 ≤ i ≤ 5$ three bits are used, |
| − | * for $6 ≤ i ≤ 19$ four bits, | + | * for $6 ≤ i ≤ 19$ four bits are used, |
| − | * for $14 ≤ i ≤ 29$ five bits, | + | * for $14 ≤ i ≤ 29$ five bits are used, |
| − | we get from the "continuous decoder input string" | + | we get from the "continuous decoder input string" |
:$$\boldsymbol{\rm 00 000 001 010 100 0001 1000 0111 0001 0001 0011 1011 1011 01101 00011 01001}$$ | :$$\boldsymbol{\rm 00 000 001 010 100 0001 1000 0111 0001 0001 0011 1011 1011 01101 00011 01001}$$ | ||
| − | to the "divided decoder input string" $($designated $I_1$, ... , $I_{16})$: | + | to the "divided decoder input string" $($designated $I_1$, ... , $I_{16})$: |
:$$\boldsymbol{\rm 00 |000 |001 |010 |100 |0001 |1000 |0111 | 0001 |0001 |0011 |1011 |1011 |01101 |00011 |01001} | :$$\boldsymbol{\rm 00 |000 |001 |010 |100 |0001 |1000 |0111 | 0001 |0001 |0011 |1011 |1011 |01101 |00011 |01001} | ||
\hspace{0.1cm}.$$ | \hspace{0.1cm}.$$ | ||
| − | + | Thus the results sought for the decoding steps $i = 5$, ... , $i = 8$: | |
* $I_5 =$ <b>100</b> (binary) <u> = 4</u> (decimal) ⇒ <b>AA</b>, | * $I_5 =$ <b>100</b> (binary) <u> = 4</u> (decimal) ⇒ <b>AA</b>, | ||
* $I_6 =$ <b>0001</b> (binary) <u> = 1</u> (decimal) ⇒ <b>B</b>, | * $I_6 =$ <b>0001</b> (binary) <u> = 1</u> (decimal) ⇒ <b>B</b>, | ||
| Line 132: | Line 132: | ||
| − | '''(4)''' Correct are <u>statements 1 and 4</u>. Reason: | + | '''(4)''' Correct are the<u>statements 1 and 4</u>. Reason: |
| − | * The new incoming index is $18$ (decimal) and in the dictionary the entry <b>DB</b> is found under the index $I = 18$ | + | * The new incoming index is $18$ (decimal) and in the dictionary the entry "<b>DB</b>" is found under the index $I = 18$. |
* For the decoding step $i = 17$ , the line $I = 19$ is entered into the dictionary. | * For the decoding step $i = 17$ , the line $I = 19$ is entered into the dictionary. | ||
| − | * The entry <b>BAD</b> is composed of the decoding result from step $i = 16$ $($<b>BA</b>$)$ and the first character $($<b>D</b>$)$ of the new result <b>DB</b>. | + | * The entry "<b>BAD</b>" is composed of the decoding result from step $i = 16$ $($<b>BA</b>$)$ and the first character $($<b>D</b>$)$ of the new result "<b>DB</b>". |
| Line 143: | Line 143: | ||
* Two bits are sufficient for the first phrase. | * Two bits are sufficient for the first phrase. | ||
* For the phrases $I_2$, ... , $I_5$ three bits are needed. | * For the phrases $I_2$, ... , $I_5$ three bits are needed. | ||
| − | * | + | * The phrases $I_6$, ... , $I_{13}$ require four bits. |
| − | * | + | * The phrases $I_{14}$, ... , $I_{29}$ require five bits. |
| − | * | + | * The phrases $I_{30}$, ... , $I_{58}$ require six bits. |
*This gives the total number of bits: | *This gives the total number of bits: | ||
| − | :$$N_{\rm | + | :$$N_{\rm bits} = 1 \cdot 2 + 4 \cdot 3 + 8 \cdot 4 + 16 \cdot 5 + 29 \cdot 6 = 300 \hspace{0.05cm}.$$ |
*With a uniform bit length (six bits for each index), $58 · 6 = 348$ bits (i.e. more) would be required ⇒ statement 2 is wrong in principle. | *With a uniform bit length (six bits for each index), $58 · 6 = 348$ bits (i.e. more) would be required ⇒ statement 2 is wrong in principle. | ||
| Line 154: | Line 154: | ||
Now to the third statement, which is also not true: | Now to the third statement, which is also not true: | ||
| − | * With the uncoded transmission of $N = 150$ characters from the symbol set $\{$ <b>A</b>, | + | * With the uncoded transmission of $N = 150$ characters from the symbol set $\{$ <b>A</b>, <b>B</b>, <b>C</b>, <b>D</b> $\}$ one would need exactly $300$ bits. With LZW one certainly needs more bits if the source is redundancy-free ⇒ characters equally likely and statistically independent. |
| − | * With redundant source with ( | + | * With a redundant source with (e.g.) $H = 1.6$ bit/source symbol, one can limit the number of bits to $N_{\rm bits} = N \cdot H$, provided it is a very large file $(N \to \infty)$. |
| − | * With a rather small file – as here only | + | * With a rather small file – as here with only $N = 150$ bits – it is not possible to say whether $N_{\rm bits}$ will be less than, equal to or greater than $150 · 1.6 = 240$. |
| − | * $N_{\rm | + | *Also quite possible is $N_{\rm bits} > 300$. In that case, it is better to do without the "Lempel–Ziv compression". |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 13:11, 10 August 2021
The compression algorithm "LZW" – named after the inventors Abraham Lempel, Jacob Ziv and Terry Welch – works like "LZ78" with a global dictionary. In this case, all possible characters – in the example A, B, C, D – are preassigned at the beginning and are successively expanded during encoding.
During decoding, exactly the same dictionary is created, only the same entry with index $I$ is made one step later than during encoding. To designate the decoding steps, we use the variable $i$.
Here are some more notes on LZW encoding and decoding:
- During encoding, at each time $i$, a search is made in the dictionary for the longest possible character string that matches the input string currently present.
- The dictionary index $I_i$ found is always transmitted in binary form. At the same time, $W(I_i) + Z$ is entered into the dictionary under the next free index.
- Here, $W(I_i)$ denotes a character or a character string, and $Z$ is the first character of the upcoming input string (i.e. also a character), which is no longer considered in $W(I_i)$ .
- With $M = 4$ possible characters, the first index $I_1$ is transmitted with two bits, the indices $I_2$, ... , $I_5$ with three bits, the next eight indices with four bits, then 16 indices with five bits, etc. The reason for this bit-saving measure can be found in the solution to this task.
After coding in the manner described here over $16$ coding steps, the following binary sequence of length $N_{\rm bit} = 61$:
- $$\boldsymbol{\rm 00 \ 000 \ 001 \ 010 \ 100 \ 0001 \ 1000 \ 0111 \ 0001 \ 0001 \ 0011 \ 1011 \ 1011 \ 01101 \ 00011 \ 01001}\hspace{0.05cm}.$$
The task of the decoder (more precisely: your task) is now,
- to reconstruct from this binary sequence the indices $I_1$, ... , $I_{16}$ taking into account the different number of bits (description of the 16 decoding results by decimal numbers),
- then read out the corresponding characters or character sequences from the dictionary according to the indices and finally – with one step delay – generate the new dictionary entry.
Hints:
- The exercise belongs to the chapter Compression according to Lempel, Ziv and Welch.
- In particular, reference is made to the pages
- Exercise 2.3 and Exercise 2.3Z deal with other Lempel-Ziv methods in a similar way.
Questions
Solution
- In contrast, three bits are already required for step $i = 2$. If the input sequence had started with AAA , the LZW coding $I_2 = I(i = 2)$ would have resulted in the decimal value $4$. This can no longer be represented with two bits and must be coded with three bits, just like $I_3$, $I_4$ and $I_5$.
- The given input string:$$\boldsymbol{\rm 00 000 001 010 100 0001}\hspace{0.05cm}...$$
- must therefore be divided by the decoder as follows:
- $$\boldsymbol{\rm 00 |000 |001 |010 |100 |0001|}\hspace{0.05cm}...$$
- The decoder results of the first four steps are therefore:
- $I_1 =$ 00 (binary) = 0 (decimal) ⇒ A,
- $I_2 =$ 000 (binary) = 0 (decimal) ⇒ A,
- $I_3 =$ 001 (binary) = 1 (decimal) ⇒ B,
- $I_4 =$ 010 (binary) = 2 (decimal) ⇒ C.
(2) If one takes into account that
- for $i = 1$ two bits are used,
- for $2 ≤ i ≤ 5$ three bits are used,
- for $6 ≤ i ≤ 19$ four bits are used,
- for $14 ≤ i ≤ 29$ five bits are used,
we get from the "continuous decoder input string"
- $$\boldsymbol{\rm 00 000 001 010 100 0001 1000 0111 0001 0001 0011 1011 1011 01101 00011 01001}$$
to the "divided decoder input string" $($designated $I_1$, ... , $I_{16})$:
- $$\boldsymbol{\rm 00 |000 |001 |010 |100 |0001 |1000 |0111 | 0001 |0001 |0011 |1011 |1011 |01101 |00011 |01001} \hspace{0.1cm}.$$
Thus the results sought for the decoding steps $i = 5$, ... , $i = 8$:
- $I_5 =$ 100 (binary) = 4 (decimal) ⇒ AA,
- $I_6 =$ 0001 (binary) = 1 (decimal) ⇒ B,
- $I_7 =$ 1000 (binary) = 8 (decimal) ⇒ AAB,
- $I_8 =$ 0111 (binary) = 7 (decimal) ⇒ CA.
(3) Statement 2 is correct.
- The following decoding results are obtained (in abbreviated form):
- $I_{9} = 1$ ⇒ B, $\hspace{0.5cm}I_{10} = 1$ ⇒ B,$\hspace{0.5cm}I_{11} = 3$ ⇒ D,$\hspace{0.5cm}I_{12} = 11$ ⇒ CAB,
- $I_{13} = 11$ ⇒ CAB,$\hspace{0.5cm}I_{14} = 13$ ⇒ BD,$\hspace{0.5cm}I_{15} = 3$ ⇒ D,$\hspace{0.5cm}I_{16} = 9$ ⇒ BA.
(4) Correct are thestatements 1 and 4. Reason:
- The new incoming index is $18$ (decimal) and in the dictionary the entry "DB" is found under the index $I = 18$.
- For the decoding step $i = 17$ , the line $I = 19$ is entered into the dictionary.
- The entry "BAD" is composed of the decoding result from step $i = 16$ $($BA$)$ and the first character $($D$)$ of the new result "DB".
(5) Only statement 1 is correct here:
- Two bits are sufficient for the first phrase.
- For the phrases $I_2$, ... , $I_5$ three bits are needed.
- The phrases $I_6$, ... , $I_{13}$ require four bits.
- The phrases $I_{14}$, ... , $I_{29}$ require five bits.
- The phrases $I_{30}$, ... , $I_{58}$ require six bits.
- This gives the total number of bits:
- $$N_{\rm bits} = 1 \cdot 2 + 4 \cdot 3 + 8 \cdot 4 + 16 \cdot 5 + 29 \cdot 6 = 300 \hspace{0.05cm}.$$
- With a uniform bit length (six bits for each index), $58 · 6 = 348$ bits (i.e. more) would be required ⇒ statement 2 is wrong in principle.
Now to the third statement, which is also not true:
- With the uncoded transmission of $N = 150$ characters from the symbol set $\{$ A, B, C, D $\}$ one would need exactly $300$ bits. With LZW one certainly needs more bits if the source is redundancy-free ⇒ characters equally likely and statistically independent.
- With a redundant source with (e.g.) $H = 1.6$ bit/source symbol, one can limit the number of bits to $N_{\rm bits} = N \cdot H$, provided it is a very large file $(N \to \infty)$.
- With a rather small file – as here with only $N = 150$ bits – it is not possible to say whether $N_{\rm bits}$ will be less than, equal to or greater than $150 · 1.6 = 240$.
- Also quite possible is $N_{\rm bits} > 300$. In that case, it is better to do without the "Lempel–Ziv compression".