Difference between revisions of "Aufgaben:Exercise 1.2: Distortions? Or no Distortion?"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Qualitätskriterien }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type=…“) |
|||
| (41 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Quality_Criteria |
}} | }} | ||
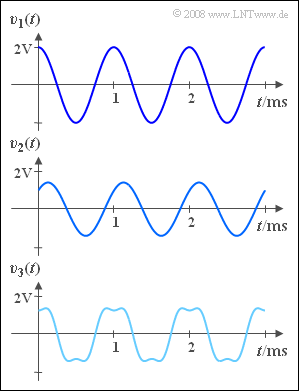
| − | [[File:|right|]] | + | [[File:P_ID949__Mod_A_1_2.png|right|frame|Observed sink signals for the <br>given input signal $q(t)$]] |
| + | The communication systems $S_1$, $S_2$ and $S_3$ are analyzed in terms of the distortions they cause. For this purpose, the cosine-shaped test signal with signal frequency $f_{\rm N} = 1\text{ kHz}$ is applied to the input of each system: | ||
| + | :$$q(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )$$ | ||
| + | The three signals at the system output are measured, as shown in the graph: | ||
| + | :$$v_1(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )\hspace{0.05cm},$$ | ||
| + | :$$v_2(t) = 1 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t + 1 \;{\rm V} \cdot \sin(2 \pi f_{\rm N} t) \hspace{0.05cm},$$ | ||
| + | :$$v_3(t)= 1.5 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t) - 0.3 \;{\rm V} \cdot \cos(6 \pi f_{\rm N} t)\hspace{0.05cm}.$$ | ||
| − | === | + | The noise components that are always present in practice will be assumed to be negligible here. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *This exercise belongs to the chapter [[Modulation_Methods/Quality_Criteria|Quality criteria]]. Particular reference is made to the page [[Modulation_Methods/Quality_Criteria#Signal.E2.80.93to.E2.80.93noise_.28power.29_ratio|Signal-to-noise power ratio]] and to the chapter [[Linear_and_Time_Invariant_Systems/Nonlinear_Distortions|Non-linear distortions]] in the book "Linear and Time-Invariant Systems". | ||
| + | *For nonlinear distortion, the sink SNR is $ρ_v = 1/K^2$, where the distortion factor $K$ is the ratio of the rms values of all harmonics to the rms value of the fundamental frequency. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What statements can be made about the $S_1$ system after this measurement? |
|type="[]"} | |type="[]"} | ||
| − | + | + $S_1$ could be an ideal system. | |
| − | + | + | + $S_1$ could be a distortionless system. |
| + | + $S_1$ could be a linearly distorting system. | ||
| + | - $S_1$ could be a nonlinearly distorting system. | ||
| − | { | + | {Write the second signal in the form $v_2(t) = α · q(t - τ)$ and determine its paramaters. |
|type="{}"} | |type="{}"} | ||
| − | $\alpha$ | + | $\alpha \ = \ $ { 0.707 3% } |
| + | $τ \ = \ $ { 125 3% } $\ \rm µ s$ | ||
| + | |||
| + | {What statements can be made about the $S_2$ system after this measurement? | ||
| + | |type="[]"} | ||
| + | - $S_2$ could be an ideal system. | ||
| + | + $S_2$ could be a distortionless system. | ||
| + | + $S_2$ could be a linearly distorting system. | ||
| + | - $S_2$ could be a nonlinearly distorting system. | ||
| + | |||
| + | {What kind of distortions are present in System $S_3$? | ||
| + | |type="()"} | ||
| + | - They are linear distortions. | ||
| + | + They are nonlinear distortions. | ||
| + | {Calculate the sink SNR $ρ_{v3}$ of System $S_3$. | ||
| + | |type="{}"} | ||
| + | $ρ_{v3} \ = \ $ { 25 3% } | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' <u>Answers 1, 2 and 3</u> are correct: |
| − | '''2 | + | *System $S_1$ could well be an ideal system, namely if for all frequencies $f_{\rm N}$ the condition $v(t) = q(t)$ were satisfied. |
| − | '''3 | + | *The second alternative is also possible, since the ideal system is a special case of distortion-free systems. |
| − | ''' | + | *However, if at a different message frequency $f_{\rm N} \ne 1$ kHz the condition $v(t) = q(t)$ were not satisfied, then a linearly distorting system would exist whose frequency response would happen to be equal to $1$ at frequency $f_{\rm N}$ . |
| − | ''' | + | *In contrast, a nonlinearly distorting system (Answer 4) can be excluded due to the lack of harmonics. |
| − | ''' | + | |
| − | + | ||
| + | |||
| + | '''(2)''' Following the explanations in the chapter "Harmonic Oscillation" in the book "Signal Representation" the following equations apply: | ||
| + | :$$A \cdot \cos(\omega_{\rm N} t ) + B \cdot \sin(\omega_{\rm N} t ) = C \cdot \cos(\omega_{\rm N} t - \varphi)\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} C = \sqrt{A^2 + B^2},\hspace{0.5cm}\varphi ={\rm arctan}\hspace{0.1cm} ({A}/{B})\hspace{0.05cm}$$ | ||
| + | *Applied to the present example, one obtains | ||
| + | :$$C = \sqrt{(1 \,{\rm V})^2 + (1 \,{\rm V})^2}= 1.414\,{\rm V}\hspace{0.05cm}.$$ | ||
| + | *The damping ratio of the system thus takes the value $α = 1.414/2 \hspace{0.15cm}\underline{= 0.707}$, and the following applies to the phase: | ||
| + | :$$ \varphi ={\rm arctan}\hspace{0.1cm}\frac {1 \,{\rm V}}{1 \,{\rm V}} = 45^{\circ} = {\pi}/{4}\hspace{0.05cm}.$$ | ||
| + | *The transformation $\cos(\omega_{\rm N} t - \varphi)= \cos[\omega_{\rm N} (t - \tau)]$ enables claims about the running time: | ||
| + | :$$\tau =\frac {\varphi}{2\pi f_{\rm N}} = \frac {\pi /4}{2\pi f_{\rm N}} = \frac {1}{8 \cdot 1 \,{\rm kHz}} \hspace{0.15cm}\underline {= 125\,{\rm µ s}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' <u>Answers 2 and 3</u> are correct: | ||
| + | *Applying the logic from subtask '''(1)''', the system $S_2$ is neither ideal nor nonlinearly distorting. | ||
| + | *In contrast, options 2 and 3 are possible, depending on whether the calculated values of $α$ and $τ$ are preserved for all frequencies or not. | ||
| + | *However, with just a single measurement at only one frequency, this cannot be clarified. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' The signal $v_3(t)$ contains a third order harmonic. Therefore, the distortion is nonlinear ⇒ <u>Answer 2</u>. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' The amplitudes $A_1 = 1.5 \ \rm V$ and $A_3 = -0.3\ \rm V$ give the distortion factor: | ||
| + | :$$ K_3 =\frac {|A_3|}{|A_1|} = 0.2\hspace{0.05cm}.$$ | ||
| + | *Therefore, according to the given equation, the sink SNR is $ρ_{v3} = 1/K_3^{ 2 } = 25$. | ||
| + | |||
| + | |||
| + | The same result is obtained from the more general calculation. | ||
| + | |||
| + | *From the amplitudes of the source signal and the fundamental wave of the sink signal, we get a frequency-independent damping factor of: | ||
| + | :$$ \alpha =\frac {1.5 \,{\rm V}}{2 \,{\rm V}} = 0.75\hspace{0.05cm}.$$ | ||
| + | *Therefore, the error signal coming from the nonlinear distortions is: | ||
| + | :$$\varepsilon_3(t) = v_3(t) - \alpha \cdot q(t) = - 0.3 \,{\rm V} \cdot \cos(6 \pi f_{\rm N} t)\hspace{0.05cm}.$$ | ||
| + | *This gives a distortion power of: | ||
| + | :$$P_{\varepsilon 3}= {1}/{2} \cdot (0.3 \,{\rm V})^2 = 0.045 \,{\rm V}^2\hspace{0.05cm}.$$ | ||
| + | *Together with the power of the source signal, | ||
| + | :$$P_{q}= {1}/{2} \cdot (2\,{\rm V})^2 = 2 \,{\rm V}^2\hspace{0.05cm},$$ | ||
| + | :and taking into account the damping factor $ \alpha = 0.75 $ just calculated, we obtain: | ||
| + | :$$\rho_{v3} = \frac{\alpha^2 \cdot P_{q}}{P_{\varepsilon 3}} = \frac{0.75^2 \cdot 2 {\rm V}^2}{0.045 } \hspace{0.15cm}\underline {= 25}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^1.2 Quality Criteria^]] |
Latest revision as of 17:16, 10 April 2022
The communication systems $S_1$, $S_2$ and $S_3$ are analyzed in terms of the distortions they cause. For this purpose, the cosine-shaped test signal with signal frequency $f_{\rm N} = 1\text{ kHz}$ is applied to the input of each system:
- $$q(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )$$
The three signals at the system output are measured, as shown in the graph:
- $$v_1(t) = 2 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t )\hspace{0.05cm},$$
- $$v_2(t) = 1 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t + 1 \;{\rm V} \cdot \sin(2 \pi f_{\rm N} t) \hspace{0.05cm},$$
- $$v_3(t)= 1.5 \;{\rm V} \cdot \cos(2 \pi f_{\rm N} t) - 0.3 \;{\rm V} \cdot \cos(6 \pi f_{\rm N} t)\hspace{0.05cm}.$$
The noise components that are always present in practice will be assumed to be negligible here.
Hints:
- This exercise belongs to the chapter Quality criteria. Particular reference is made to the page Signal-to-noise power ratio and to the chapter Non-linear distortions in the book "Linear and Time-Invariant Systems".
- For nonlinear distortion, the sink SNR is $ρ_v = 1/K^2$, where the distortion factor $K$ is the ratio of the rms values of all harmonics to the rms value of the fundamental frequency.
Questions
Solution
- System $S_1$ could well be an ideal system, namely if for all frequencies $f_{\rm N}$ the condition $v(t) = q(t)$ were satisfied.
- The second alternative is also possible, since the ideal system is a special case of distortion-free systems.
- However, if at a different message frequency $f_{\rm N} \ne 1$ kHz the condition $v(t) = q(t)$ were not satisfied, then a linearly distorting system would exist whose frequency response would happen to be equal to $1$ at frequency $f_{\rm N}$ .
- In contrast, a nonlinearly distorting system (Answer 4) can be excluded due to the lack of harmonics.
(2) Following the explanations in the chapter "Harmonic Oscillation" in the book "Signal Representation" the following equations apply:
- $$A \cdot \cos(\omega_{\rm N} t ) + B \cdot \sin(\omega_{\rm N} t ) = C \cdot \cos(\omega_{\rm N} t - \varphi)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} C = \sqrt{A^2 + B^2},\hspace{0.5cm}\varphi ={\rm arctan}\hspace{0.1cm} ({A}/{B})\hspace{0.05cm}$$
- Applied to the present example, one obtains
- $$C = \sqrt{(1 \,{\rm V})^2 + (1 \,{\rm V})^2}= 1.414\,{\rm V}\hspace{0.05cm}.$$
- The damping ratio of the system thus takes the value $α = 1.414/2 \hspace{0.15cm}\underline{= 0.707}$, and the following applies to the phase:
- $$ \varphi ={\rm arctan}\hspace{0.1cm}\frac {1 \,{\rm V}}{1 \,{\rm V}} = 45^{\circ} = {\pi}/{4}\hspace{0.05cm}.$$
- The transformation $\cos(\omega_{\rm N} t - \varphi)= \cos[\omega_{\rm N} (t - \tau)]$ enables claims about the running time:
- $$\tau =\frac {\varphi}{2\pi f_{\rm N}} = \frac {\pi /4}{2\pi f_{\rm N}} = \frac {1}{8 \cdot 1 \,{\rm kHz}} \hspace{0.15cm}\underline {= 125\,{\rm µ s}}\hspace{0.05cm}.$$
(3) Answers 2 and 3 are correct:
- Applying the logic from subtask (1), the system $S_2$ is neither ideal nor nonlinearly distorting.
- In contrast, options 2 and 3 are possible, depending on whether the calculated values of $α$ and $τ$ are preserved for all frequencies or not.
- However, with just a single measurement at only one frequency, this cannot be clarified.
(4) The signal $v_3(t)$ contains a third order harmonic. Therefore, the distortion is nonlinear ⇒ Answer 2.
(5) The amplitudes $A_1 = 1.5 \ \rm V$ and $A_3 = -0.3\ \rm V$ give the distortion factor:
- $$ K_3 =\frac {|A_3|}{|A_1|} = 0.2\hspace{0.05cm}.$$
- Therefore, according to the given equation, the sink SNR is $ρ_{v3} = 1/K_3^{ 2 } = 25$.
The same result is obtained from the more general calculation.
- From the amplitudes of the source signal and the fundamental wave of the sink signal, we get a frequency-independent damping factor of:
- $$ \alpha =\frac {1.5 \,{\rm V}}{2 \,{\rm V}} = 0.75\hspace{0.05cm}.$$
- Therefore, the error signal coming from the nonlinear distortions is:
- $$\varepsilon_3(t) = v_3(t) - \alpha \cdot q(t) = - 0.3 \,{\rm V} \cdot \cos(6 \pi f_{\rm N} t)\hspace{0.05cm}.$$
- This gives a distortion power of:
- $$P_{\varepsilon 3}= {1}/{2} \cdot (0.3 \,{\rm V})^2 = 0.045 \,{\rm V}^2\hspace{0.05cm}.$$
- Together with the power of the source signal,
- $$P_{q}= {1}/{2} \cdot (2\,{\rm V})^2 = 2 \,{\rm V}^2\hspace{0.05cm},$$
- and taking into account the damping factor $ \alpha = 0.75 $ just calculated, we obtain:
- $$\rho_{v3} = \frac{\alpha^2 \cdot P_{q}}{P_{\varepsilon 3}} = \frac{0.75^2 \cdot 2 {\rm V}^2}{0.045 } \hspace{0.15cm}\underline {= 25}\hspace{0.05cm}.$$