Difference between revisions of "Aufgaben:Exercise 4.12: Root-Nyquist Systems"
| (35 intermediate revisions by 4 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1722__Mod_A_4_11.png|right|]] | + | [[File:P_ID1722__Mod_A_4_11.png|right|frame|Spectra of transmission pulse (above) and detection pulse (below)]] |
| − | + | In "quadrature amplitude modulation" $\rm (QAM)$ systems, the "root-Nyquist variant" is often chosen (which gets its name from the spectral range) instead of a rectangular basic transmission pulse. The reason for this is the significantly smaller bandwidth. | |
| − | In | + | *In this case, the basic detection pulse $g_d(t)$ satisfies the [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems#First_Nyquist_criterion_in_the_time_domain|first Nyquist criterion]], since $G_d(f)$ is point-symmetric about the so-called "Nyquist frequency" $f_{\rm Nyq} = 1/T$ . |
| + | *$G_d(f)$ is a [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Raised-cosine_low-pass_filter|raised-cosine spectrum]], where the rolloff factor $r$ can take values from $0$ to $1$ (including these limits). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Furthermore, the following holds for the Nyquist frequency response: | |
| − | $ | + | * When $|f| < f_1 = f_{\rm Nyq} · (1 – r)$ ⇒ $G_d(f)$ is constant and equal to $g_0 · T$. |
| + | * At frequencies greater than $f_2 = f_{\rm Nyq} · (1 + r)$ ⇒ $G_d(f)$ has no components. | ||
| + | * In between, the slope is cosine. | ||
| − | |||
| − | |||
| − | |||
| − | + | The optimization of digital communication systems requires that the receiver frequency response $H_{\rm E}(f)$ should be of the same shape as the transmission spectrum $G_s(f)$ . | |
| + | To obtain dimensionally correct spectral functions for this task and the graph, it is assumed that | ||
| + | :$$G_s(f) = \sqrt{g_0 \cdot T \cdot G_d(f)},$$ | ||
| + | :$$ H_{\rm E}(f) = \frac{1}{g_0 \cdot T}\cdot G_s(f)\hspace{0.05cm}.$$ | ||
| − | === | + | The top graph shows the transmission spectrum $G_s(f)$ for the rolloff factors |
| + | *$r = 0$ (green dotted rectangle), | ||
| + | *$r = 0.5$ (blue solid curve), | ||
| + | *$r = 1$ (red dashed curve). | ||
| + | |||
| + | |||
| + | Below, the spectrum $G_d(f)$ of the basic detection pulse before the decider is shown in the same colors. | ||
| + | *The associated pulse $g_d(t)$ is a [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems#First_Nyquist_criterion_in_the_time_domain|Nyquist pulse]] for all valid rolloff factors $(0 ≤ r ≤ 1)$ as opposed to the basic transmission pulse $g_s(t)$. | ||
| + | *For this, the following equation is given in the literature - for example in '''[Kam04]''' : | ||
| + | :$$g_s(t) = g_0 \cdot \frac{4 r t/T \cdot \cos \left [\pi \cdot (1+r) \cdot t/T \right ]+ \sin \left [\pi \cdot (1-r) \cdot t/T \right ]}{\left [1- (4 r t/T)^2 \right ] \cdot \pi \cdot t/T}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *This exercise belongs to the chapter [[Modulation_Methods/Quadrature_Amplitude_Modulation|"Quadrature Amplitude Modulation"]]. | ||
| + | *Particular reference is made to the page [[Modulation_Methods/Quadrature_Amplitude_Modulation#Nyquist_and_Root-Nyquist_QAM_systems|"Nyquist and Root-Nyquist systems"]] in this chapter. | ||
| + | *Further useful informations can be found in the chapter [[Digital_Signal_Transmission/Properties_of_Nyquist_Systems|Properties of Nyquist Systems]] in the book "Digital Signal Transmission". | ||
| + | * '''[Kam04]''' refers to the textbook "Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004". | ||
| + | *Energies are to be specified in $\rm V^2s$; they thus refer to the reference resistance $R = 1 \ \rm \Omega$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the basic transmission pulse $g_s(t)$ for the rolloff factor $r = 0$? What is the signal value at time $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $g_s(t = 0) \ = \ $ { 1 3% } $\ \cdot g_0$ |
| − | { | + | {What is the basic transmission pulse $g_s(t)$ for the rolloff factor $r = 1$? What is the signal value at time $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $g_s(t = 0) \ = \ $ { 1.273 3% } $\ \cdot g_0$ |
| − | { | + | {Let $r = 1$. At what times does $g_s(t)$ cross the axis? |
| − | |type=" | + | |type="()"} |
| − | - | + | - At all multiples of the symbol duration $T$. |
| − | - | + | - At $t = ±0.25 T, \ ±0.75 T, \ ±1.25 T, \ ±1.75 T$, ... |
| − | + | + | + At $t = ±0.75 T, \ ±1.25 T,\ ±1.75 T$, ... |
| − | { | + | {What is the basic transmission pulse $g_s(t)$ for the rolloff factor $r = 0.5$? What is the signal value at time $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $g_s(t = 0) \ = \ $ { 1.137 3% } $\ \cdot g_0$ |
| − | { | + | {Which statements are valid for the pulse amplitude, independent of $r$ ? Solve using the frequency domain. |
| − | |type=" | + | |type="()"} |
| − | - | + | - The pulse amplitude can take any value in the range $0 ≤ g_s(t = 0) ≤ g_0$ . |
| − | - | + | - The pulse amplitude can take any value in the range $g_0 ≤ g_s(t = 0) ≤ 2 g_0$ . |
| − | + | + | + The pulse amplitude can take any value in the range $g_0 ≤ g_s(t = 0) ≤ 4 g_0/π$ . |
| − | { | + | {What is the energy $E_{g_s}$ of the basic transmission pulse $g_s(t)$ when $r = 0$ and $r = 1$? |
|type="{}"} | |type="{}"} | ||
| − | $ r = 0: | + | $r = 0\text{:} \ \ \ \ E_{g_s} \ = \ $ { 1 3% } $\ \cdot g_0^2 \cdot T$ |
| − | $ r = 1: | + | $r = 1\text{:} \ \ \ \ E_{g_s} \ = \ $ { 1 3% } $\ \cdot g_0^2 \cdot T$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' If we substitute $r = 0$ into the given equation, the first terms in the numerator and denominator disappear and we get: |
| − | $$g_s(t) = g_0 \cdot \frac{\sin \left (\pi \cdot t/T \right )}{\pi \cdot t/T} = g_0 \cdot {\rm | + | : $$g_s(t) = g_0 \cdot \frac{\sin \left (\pi \cdot t/T \right )}{\pi \cdot t/T} = g_0 \cdot {\rm sinc} \left ( {t}/{T} \right )\hspace{0.05cm}.$$ |
| − | + | *At time $t = 0$, ${\rm sinc} \left ( {t}/{T} \right ) =g_0$: | |
| − | $$ g_s(t) \hspace{0.15cm}\underline { = 1. | + | :$$ g_s(t) \hspace{0.15cm}\underline { = 1.0 } \cdot g_0 \hspace{0.05cm}.$$ |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' When $r = 1$, the given equation simplies as follows: | ||
| + | :$$g_s(t) = \frac{4 \cdot g_0}{\pi} \cdot \frac{ \cos \left (2 \pi \cdot t/T \right )}{\left [1- (4 t/T)^2 \right ] }\hspace{0.3cm}\Rightarrow \hspace{0.3cm} g_s(t = 0) = \frac{4 \cdot g_0}{\pi} \hspace{0.15cm}\underline {= 1.273 }\cdot g_0 \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' The <u>last answer</u> is correct: | ||
| + | *Zero intercepts are only possible for $r = 1$ if the cosine function in the numerator is zero, that is, for all integer values of $k$: | ||
| + | :$$2 \pi \cdot t/T = {\pi}/{2} + k \cdot \pi \hspace{0.3cm}\Rightarrow \hspace{0.3cm} t = \pm 0.25T, \hspace{0.15cm} \pm 0.75T, \hspace{0.15cm}\pm 1.25T, \hspace{0.15cm} ...$$ | ||
| + | *However, only the last answer is correct, since the zero values at $±0.25T$ are cancelled by the zero in the denominator. | ||
| + | *Applying de l'Hospital's rule yields $g_s(t = ± 0.25T) = g_0$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' With $r = 0.5$ and the shortcut $x = t/T$, one gets: | ||
| + | :$$g_s(x) = \frac{g_0}{\pi} \cdot \frac{2 \cdot x \cdot \cos \left (1.5\pi \cdot x \right )+ \sin \left (0.5\pi \cdot x \right )}{\left (1- 4 \cdot x^2 \right ) \cdot x}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *For the calculation at time $t = 0$, de l'Hospital's rule must be applied. | ||
| + | *The derivatives of the numerator and denominator give: | ||
| + | :$$Z'(x) = 2 \cdot \cos \left (1.5\pi \cdot x \right ) - 3 \pi \cdot x \cdot \sin \left (1.5\pi \cdot x \right ) + 0.5 \pi \cdot \cos \left (0.5\pi \cdot x \right ),$$ | ||
| + | [[File:P_ID1723__Mod_A_4_11b.png|right|frame|Basic transmission pulse (root-Nyquist) and basic detection pulse (Nyquist)]] | ||
| + | |||
| + | :$$N'(x) = \left (1- 4 \cdot x^2 \right ) - 8 \cdot x^2 \hspace{0.05cm}.$$ | ||
| + | *The two boundary transitions for $x → 0$ yield: | ||
| + | :$$\lim_{x \rightarrow 0} Z'(x) = 2 +{\pi }/{2},\hspace{0.2cm} \lim_{x \rightarrow 0} N'(x) = 1 \hspace{0.05cm}.$$ | ||
| + | *Thus, for the signal amplitude at time $t = 0$: | ||
| + | :$$g_s(t=0) = \frac{g_0}{\pi} \cdot \left ( 2 +{\pi }/{2} \right ) = {g_0} \cdot \left ( 0.5 + {2}/{\pi } \right )\hspace{0.15cm}\underline {= 1.137} \cdot g_0 \hspace{0.05cm}.$$ | ||
| + | |||
| + | Here, the graph illustrates the results calculated again: | ||
| + | *$g_d(t)$ is a Nyquist pulse, meaning that it has zero crossings at least at all multiples of the symbol duration $T$ (and possibly others depending on the rolloff factor). | ||
| + | *On the other hand, the pulse $g_s(t)$ does not satisfy the Nyquist criterion. Moreover, from this plot one can once again see that for $r ≠ 0$ the pulse amplitude $g_s(t = 0)$ is always larger than $g_0$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''4 | + | '''(5)''' The <u>last answer</u> is correct $($the first answer is ruled out from the results in questions '''(2)''' and '''(4)''' $)$. The validity of the lower bound $g_0$ and the upper bound $4g_0/π$ can be proved as follows: |
| − | $$g_s( | + | * The pulse amplitude $g_s(t = 0)$ is generally equal to the area under the spectral function $G_s(f)$. |
| + | * The smallest area is obtained for $r = 0$. Here, $G_s(f) = g_0 · T$ is in the range $|f| < ±1/(2T)$. Thus, the area is equal to $g_0$. | ||
| + | * The largest area is obtained for $r = 1$. Here, $G_s(f)$ extends to the range $±1/T$ and has a cosine shape. | ||
| + | *The result $g_s(t = 0) = 4g_0/π$ was already calculated in question '''(3)''' . Though it still holds that: | ||
| + | :$$g_s(t=0) = 2 \cdot {g_0} \cdot \int_{ 0 }^{1/T} {\cos\left(\frac{\pi }{2}\cdot f \cdot T \right)}\hspace{0.1cm} {\rm d}f = \frac{4 g_0}{\pi} \cdot \int_{ 0 }^{\pi/2} {\cos\left(x \right)}\hspace{0.1cm} {\rm d}x = {4 g_0}/{\pi} \cdot \big[\sin(\pi/2) - \sin(0) \big] = {4 g_0}/{\pi}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''6 | + | '''(6)''' The energy of the basic transmission pulse $g_s(t)$ can be found in the time or frequency domain according to Parseval's theorem: |
| − | $$E_{g_s} = \int_{ -\infty }^{+\infty} {[g_s(t)]^2}\hspace{0.1cm} {\rm d}t = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$ | + | :$$E_{g_s} = \int_{ -\infty }^{+\infty} {[g_s(t)]^2}\hspace{0.1cm} {\rm d}t = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$ |
| − | + | *From the equations and graph on the exercise page, we can see that $|G_s(f)|^2$ has the same shape as $G_d(f)$, but the height is now $(g_0 · T)^2$ instead of $g_0 · T$: | |
| − | $$E_{g_s} = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f = \frac{g_0^2 \cdot T^2}{g_0 \cdot T} \cdot \int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$ | + | :$$E_{g_s} = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f = \frac{g_0^2 \cdot T^2}{g_0 \cdot T} \cdot \int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$ |
| − | + | *Due to the Nyquist form of $G_d(f)$, it holds independently of $r$: | |
| − | $$\int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f = g_0 \hspace{0.05cm}.$$ | + | :$$\int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f = g_0 \hspace{0.05cm}.$$ |
| − | + | *Thus, the pulse energy is also independent of $r$, so it is also valid for $r = 0$ and $r = 1$. In <u>both cases</u>, $E_ {g_s}\hspace{0.15cm}\underline { = 1.0} · g_0^2 · T.$ | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 103: | Line 145: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^4.3 Quadrature Amplitude Modulation^]] |
Latest revision as of 13:07, 19 April 2022
In "quadrature amplitude modulation" $\rm (QAM)$ systems, the "root-Nyquist variant" is often chosen (which gets its name from the spectral range) instead of a rectangular basic transmission pulse. The reason for this is the significantly smaller bandwidth.
- In this case, the basic detection pulse $g_d(t)$ satisfies the first Nyquist criterion, since $G_d(f)$ is point-symmetric about the so-called "Nyquist frequency" $f_{\rm Nyq} = 1/T$ .
- $G_d(f)$ is a raised-cosine spectrum, where the rolloff factor $r$ can take values from $0$ to $1$ (including these limits).
Furthermore, the following holds for the Nyquist frequency response:
- When $|f| < f_1 = f_{\rm Nyq} · (1 – r)$ ⇒ $G_d(f)$ is constant and equal to $g_0 · T$.
- At frequencies greater than $f_2 = f_{\rm Nyq} · (1 + r)$ ⇒ $G_d(f)$ has no components.
- In between, the slope is cosine.
The optimization of digital communication systems requires that the receiver frequency response $H_{\rm E}(f)$ should be of the same shape as the transmission spectrum $G_s(f)$ .
To obtain dimensionally correct spectral functions for this task and the graph, it is assumed that
- $$G_s(f) = \sqrt{g_0 \cdot T \cdot G_d(f)},$$
- $$ H_{\rm E}(f) = \frac{1}{g_0 \cdot T}\cdot G_s(f)\hspace{0.05cm}.$$
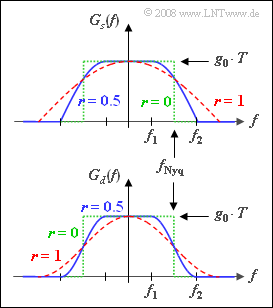
The top graph shows the transmission spectrum $G_s(f)$ for the rolloff factors
- $r = 0$ (green dotted rectangle),
- $r = 0.5$ (blue solid curve),
- $r = 1$ (red dashed curve).
Below, the spectrum $G_d(f)$ of the basic detection pulse before the decider is shown in the same colors.
- The associated pulse $g_d(t)$ is a Nyquist pulse for all valid rolloff factors $(0 ≤ r ≤ 1)$ as opposed to the basic transmission pulse $g_s(t)$.
- For this, the following equation is given in the literature - for example in [Kam04] :
- $$g_s(t) = g_0 \cdot \frac{4 r t/T \cdot \cos \left [\pi \cdot (1+r) \cdot t/T \right ]+ \sin \left [\pi \cdot (1-r) \cdot t/T \right ]}{\left [1- (4 r t/T)^2 \right ] \cdot \pi \cdot t/T}\hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Quadrature Amplitude Modulation".
- Particular reference is made to the page "Nyquist and Root-Nyquist systems" in this chapter.
- Further useful informations can be found in the chapter Properties of Nyquist Systems in the book "Digital Signal Transmission".
- [Kam04] refers to the textbook "Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004".
- Energies are to be specified in $\rm V^2s$; they thus refer to the reference resistance $R = 1 \ \rm \Omega$.
Questions
Solution
- $$g_s(t) = g_0 \cdot \frac{\sin \left (\pi \cdot t/T \right )}{\pi \cdot t/T} = g_0 \cdot {\rm sinc} \left ( {t}/{T} \right )\hspace{0.05cm}.$$
- At time $t = 0$, ${\rm sinc} \left ( {t}/{T} \right ) =g_0$:
- $$ g_s(t) \hspace{0.15cm}\underline { = 1.0 } \cdot g_0 \hspace{0.05cm}.$$
(2) When $r = 1$, the given equation simplies as follows:
- $$g_s(t) = \frac{4 \cdot g_0}{\pi} \cdot \frac{ \cos \left (2 \pi \cdot t/T \right )}{\left [1- (4 t/T)^2 \right ] }\hspace{0.3cm}\Rightarrow \hspace{0.3cm} g_s(t = 0) = \frac{4 \cdot g_0}{\pi} \hspace{0.15cm}\underline {= 1.273 }\cdot g_0 \hspace{0.05cm}.$$
(3) The last answer is correct:
- Zero intercepts are only possible for $r = 1$ if the cosine function in the numerator is zero, that is, for all integer values of $k$:
- $$2 \pi \cdot t/T = {\pi}/{2} + k \cdot \pi \hspace{0.3cm}\Rightarrow \hspace{0.3cm} t = \pm 0.25T, \hspace{0.15cm} \pm 0.75T, \hspace{0.15cm}\pm 1.25T, \hspace{0.15cm} ...$$
- However, only the last answer is correct, since the zero values at $±0.25T$ are cancelled by the zero in the denominator.
- Applying de l'Hospital's rule yields $g_s(t = ± 0.25T) = g_0$.
(4) With $r = 0.5$ and the shortcut $x = t/T$, one gets:
- $$g_s(x) = \frac{g_0}{\pi} \cdot \frac{2 \cdot x \cdot \cos \left (1.5\pi \cdot x \right )+ \sin \left (0.5\pi \cdot x \right )}{\left (1- 4 \cdot x^2 \right ) \cdot x}\hspace{0.05cm}.$$
- For the calculation at time $t = 0$, de l'Hospital's rule must be applied.
- The derivatives of the numerator and denominator give:
- $$Z'(x) = 2 \cdot \cos \left (1.5\pi \cdot x \right ) - 3 \pi \cdot x \cdot \sin \left (1.5\pi \cdot x \right ) + 0.5 \pi \cdot \cos \left (0.5\pi \cdot x \right ),$$
- $$N'(x) = \left (1- 4 \cdot x^2 \right ) - 8 \cdot x^2 \hspace{0.05cm}.$$
- The two boundary transitions for $x → 0$ yield:
- $$\lim_{x \rightarrow 0} Z'(x) = 2 +{\pi }/{2},\hspace{0.2cm} \lim_{x \rightarrow 0} N'(x) = 1 \hspace{0.05cm}.$$
- Thus, for the signal amplitude at time $t = 0$:
- $$g_s(t=0) = \frac{g_0}{\pi} \cdot \left ( 2 +{\pi }/{2} \right ) = {g_0} \cdot \left ( 0.5 + {2}/{\pi } \right )\hspace{0.15cm}\underline {= 1.137} \cdot g_0 \hspace{0.05cm}.$$
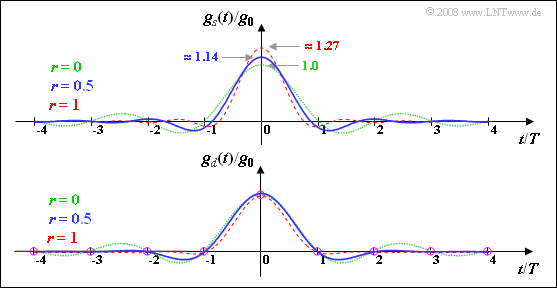
Here, the graph illustrates the results calculated again:
- $g_d(t)$ is a Nyquist pulse, meaning that it has zero crossings at least at all multiples of the symbol duration $T$ (and possibly others depending on the rolloff factor).
- On the other hand, the pulse $g_s(t)$ does not satisfy the Nyquist criterion. Moreover, from this plot one can once again see that for $r ≠ 0$ the pulse amplitude $g_s(t = 0)$ is always larger than $g_0$.
(5) The last answer is correct $($the first answer is ruled out from the results in questions (2) and (4) $)$. The validity of the lower bound $g_0$ and the upper bound $4g_0/π$ can be proved as follows:
- The pulse amplitude $g_s(t = 0)$ is generally equal to the area under the spectral function $G_s(f)$.
- The smallest area is obtained for $r = 0$. Here, $G_s(f) = g_0 · T$ is in the range $|f| < ±1/(2T)$. Thus, the area is equal to $g_0$.
- The largest area is obtained for $r = 1$. Here, $G_s(f)$ extends to the range $±1/T$ and has a cosine shape.
- The result $g_s(t = 0) = 4g_0/π$ was already calculated in question (3) . Though it still holds that:
- $$g_s(t=0) = 2 \cdot {g_0} \cdot \int_{ 0 }^{1/T} {\cos\left(\frac{\pi }{2}\cdot f \cdot T \right)}\hspace{0.1cm} {\rm d}f = \frac{4 g_0}{\pi} \cdot \int_{ 0 }^{\pi/2} {\cos\left(x \right)}\hspace{0.1cm} {\rm d}x = {4 g_0}/{\pi} \cdot \big[\sin(\pi/2) - \sin(0) \big] = {4 g_0}/{\pi}\hspace{0.05cm}.$$
(6) The energy of the basic transmission pulse $g_s(t)$ can be found in the time or frequency domain according to Parseval's theorem:
- $$E_{g_s} = \int_{ -\infty }^{+\infty} {[g_s(t)]^2}\hspace{0.1cm} {\rm d}t = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$
- From the equations and graph on the exercise page, we can see that $|G_s(f)|^2$ has the same shape as $G_d(f)$, but the height is now $(g_0 · T)^2$ instead of $g_0 · T$:
- $$E_{g_s} = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f = \frac{g_0^2 \cdot T^2}{g_0 \cdot T} \cdot \int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$
- Due to the Nyquist form of $G_d(f)$, it holds independently of $r$:
- $$\int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f = g_0 \hspace{0.05cm}.$$
- Thus, the pulse energy is also independent of $r$, so it is also valid for $r = 0$ and $r = 1$. In both cases, $E_ {g_s}\hspace{0.15cm}\underline { = 1.0} · g_0^2 · T.$