Difference between revisions of "Channel Coding/Objective of Channel Coding"
| (121 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{FirstPage}} | {{FirstPage}} | ||
{{Header| | {{Header| | ||
| − | Untermenü= | + | Untermenü=Binary Block Codes for Channel Coding |
| − | + | |Nächste Seite=Channel Models and Decision Structures | |
| − | |Nächste Seite= | ||
}} | }} | ||
| − | == | + | == # OVERVIEW OF THE FIRST MAIN CHAPTER # == |
<br> | <br> | ||
| − | + | The first chapter deals with »'''block codes for error detection and error correction'''« and provides the basics for describing more effective codes such as | |
| + | :*the »Reed-Solomon codes« (see Chapter 2), | ||
| + | :*the »convolutional codes« (see Chapter 3), and | ||
| + | :*the »iteratively decodable product codes« ("turbo codes") and the »low-density parity-check codes« (see Chapter 4). | ||
| − | |||
| − | * | + | This specific field of coding is called »'''Channel Coding'''« in contrast to |
| + | :* »Source Coding« (redundancy reduction for reasons of data compression), and | ||
| + | :* »Line Coding« (additional redundancy to adapt the digital signal to the spectral characteristics of the transmission medium).aa | ||
| − | |||
| − | + | We restrict ourselves here to »binary codes«. In detail, this book covers: | |
| − | + | #Definitions and introductory examples of »error detection and error correction«, | |
| + | #a brief review of appropriate »channel models« and »decision device structures«, | ||
| + | #known binary block codes such as »single parity-check code«, »repetition code« and »Hamming code«, | ||
| + | #the general description of linear codes using »generator matrix« and »check matrix«, | ||
| + | #the decoding possibilities for block codes, including »syndrome decoding« , | ||
| + | #simple approximations and upper bounds for the »block error probability«, and | ||
| + | #an »information-theoretic bound« on channel coding. | ||
| − | |||
| − | + | == Error detection and error correction == | |
| − | * | + | <br> |
| − | * | + | Transmission errors occur in every digital transmission system. It is possible to keep the probability $p_{\rm B}$ of such a bit error very small, for example by using a very large signal energy. However, the bit error probability $p_{\rm B} = 0$ is never achievable because of the Gaussian PDF of the thermal noise that is always present.<br> |
| + | |||
| + | Particularly in the case of heavily disturbed channels and also for safety-critical applications, it is therefore essential to provide special protection for the data to be transmitted, adapted to the application and channel. For this purpose, redundancy is added at the transmitter and this redundancy is used at the receiver to reduce the number of decoding errors. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definitions:}$ | ||
| + | |||
| + | # »'''Error Detection«''': The decoder checks the integrity of the received blocks and marks any errors found. If necessary, the receiver informs the transmitter about erroneous blocks via the return channel, so that the transmitter sends the corresponding block again.<br><br> | ||
| + | # »'''Error Correction«''': The decoder detects one (or more) bit errors and provides further information for them, for example their positions in the transmitted block. In this way, it may be possible to completely correct the errors that have occurred.<br><br> | ||
| + | # »'''Channel Coding«''' includes both, procedures for »'''error detection'''« as well as those for »'''error correction'''«.<br>}} | ||
| + | |||
| + | |||
| + | All $\rm ARQ$ ("Automatic Repeat Request") methods use error detection only. | ||
| + | *Less redundancy is required for error detection than for error correction. | ||
| + | *One disadvantage of ARQ is its low throughput when channel quality is poor, i.e. when entire blocks of data must be frequently re-requested by the receiver.<br> | ||
| + | |||
| + | |||
| + | In this book we mostly deal with $\rm FEC$ ("Forward Error Correction") which leads to very small bit error rates if the channel is sufficiently good (large SNR). | ||
| + | *With worse channel conditions, nothing changes in the throughput, i.e. the same amount of information is transmitted. | ||
| + | *However, the symbol error rate can then assume very large values.<br> | ||
| + | |||
| + | |||
| + | Often FEC and ARQ methods are combined, and the redundancy is divided between them in such a way, | ||
| + | *so that a small number of errors can still be corrected, but | ||
| + | *when there are too many errors, a repeat of the block is requested. | ||
| − | == | + | == Some introductory examples of error detection == |
<br> | <br> | ||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 1: Single Parity–Check Code $\rm (SPC)$}$ | ||
| − | + | If one adds $k = 4$ bit by a so-called "parity bit" in such a way that the sum of all ones is even, e.g. (with bold parity bits)<br> | |
| − | + | :$$0000\hspace{0.03cm}\boldsymbol{0},\ 0001\hspace{0.03cm}\boldsymbol{1}, \text{...} ,\ 1111\hspace{0.03cm}\boldsymbol{0}, \text{...}\ ,$$ | |
| − | + | it is very easy to recognize a single error. Two errors within a code word, on the other hand, remain undetected. }}<br> | |
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 2:   International Standard Book Number (ISBN)}$ | ||
| − | + | Since the 1960s, all books have been given 10-digit codes ("ISBN–10"). Since 2007, the specification according to "ISBN–13" is additionally obligatory. For example, these are for the reference book [Söd93]<ref name ='Söd93'>Söder, G.: Modellierung, Simulation und Optimierung von Nachrichtensystemen. Berlin - Heidelberg: Springer, 1993.</ref>:<br> | |
| − | + | *$\boldsymbol{3–540–57215–5}$ (for "ISBN–10"), | |
| + | |||
| + | *$\boldsymbol{978–3–54057215–2}$ (for "ISBN–13"). | ||
| − | |||
| − | + | The last digit $z_{10}$ for "ISBN–10" results from the previous digits $z_1 = 3$, $z_2 = 5$, ... , $z_9 = 5$ according to the following calculation rule: | |
| − | :<math>z_{10} = \left ( \sum_{i=1}^{9} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.3cm} \mod 11 = | + | ::<math>z_{10} = \left ( \sum_{i=1}^{9} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.3cm} \mod 11 = |
(1 \cdot 3 + 2 \cdot 5 + ... + 9 \cdot 5 ) \hspace{-0.2cm} \mod 11 = 5 | (1 \cdot 3 + 2 \cdot 5 + ... + 9 \cdot 5 ) \hspace{-0.2cm} \mod 11 = 5 | ||
\hspace{0.05cm}. </math> | \hspace{0.05cm}. </math> | ||
| − | + | :Note that $z_{10} = 10$ must be written as $z_{10} = \rm X$ (roman numeral representation of "10"), since the number $10$ cannot be represented as a digit in the decimal system.<br> | |
| − | + | The same applies to the check digit for "ISBN–13": | |
| − | :<math>z_{13 | + | ::<math>z_{13}= 10 - \left ( \sum_{i=1}^{12} \hspace{0.2cm} z_i \cdot 3^{(i+1) \hspace{-0.2cm} \mod 2} \right ) \hspace{-0.3cm} \mod 10 = 10 \hspace{-0.05cm}- \hspace{-0.05cm} \big [(9\hspace{-0.05cm}+\hspace{-0.05cm}8\hspace{-0.05cm}+\hspace{-0.05cm}5\hspace{-0.05cm}+\hspace{-0.05cm}0\hspace{-0.05cm}+\hspace{-0.05cm}7\hspace{-0.05cm}+\hspace{-0.05cm}1) \cdot 1 + (7\hspace{-0.05cm}+\hspace{-0.05cm}3\hspace{-0.05cm}+\hspace{-0.05cm}4\hspace{-0.05cm}+\hspace{-0.05cm}5\hspace{-0.05cm}+\hspace{-0.05cm}2\hspace{-0.05cm}+\hspace{-0.05cm}5) \cdot 3\big ] \hspace{-0.2cm} \mod 10 </math> |
| − | + | :: <math>\Rightarrow \hspace{0.3cm} z_{13}= 10 - (108 \hspace{-0.2cm} \mod 10) = 10 - 8 = 2 | |
| − | :<math>\hspace{0. | ||
\hspace{0.05cm}. </math> | \hspace{0.05cm}. </math> | ||
| − | + | With both variants, in contrast to the above parity check code $\rm (SPC)$, number twists such as $57 \, \leftrightarrow 75$ are also recognized, since different positions are weighted differently here}}. | |
| − | [[File: | + | {{GraueBox|TEXT= |
| + | [[File:EN_KC_T_1_1_s2.png|right|frame|One-dimensional bar code]] | ||
| + | $\text{Example 3: Bar code (one-dimensional)}$ | ||
| − | + | The most widely used error-detecting code worldwide is the "bar code" for marking products, for example according to EAN–13 ("European Article Number") with 13 digits. | |
| + | *These are represented by bars and gaps of different widths and can be easily decoded with an opto–electronic reader. | ||
| + | |||
| + | *The first three digits indicate the country (e.g. Germany: 400 ... 440), the next four or five digits producer and product. | ||
| + | |||
| + | *The last digit is the parity check digit $z_{13}$, which is calculated exactly as for ISBN–13.}} | ||
| + | |||
| + | == Some introductory examples of error correction== | ||
<br> | <br> | ||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 4: Two-dimensional bar codes for online tickets}$ | ||
| + | |||
| + | If you book a railway ticket online and print it out, you will find an example of a two-dimensional bar code, namely the [https://en.wikipedia.org/wiki/Aztec_Code $\text{Aztec code}$] developed in 1995 by Andy Longacre at the Welch Allyn company in the USA, with which amounts of data up to $3000$ characters can be encoded. Due to the [[Channel_Coding/Definition_und_Eigenschaften_von_Reed–Solomon–Codes|$\text{Reed–Solomon error correction}$]], reconstruction of the data content is still possible even if up to $40\%$ of the code has been destroyed, for example by bending the ticket or by coffee stains.<br> | ||
| + | |||
| + | On the right you see a $\rm QR\ code$ ("Quick Response") with associated content. | ||
| + | [[File:EN_KC_T_1_1_S2a_v2.png|right|frame|Two-dimensional bar codes: Aztec and QR code|class=fit]] | ||
| + | |||
| + | *The QR code was developed in 1994 for the automotive industry in Japan to mark components and also allows error correction. | ||
| + | |||
| + | *In the meantime, the use of the QR code has become very diverse. In Japan, it can be found on almost every advertising poster and on every business card. It has also been becoming more and more popular in Europe.<br> | ||
| + | |||
| + | *All two-dimensional bar codes have square markings to calibrate the reader. You can find details on this in [KM+09]<ref>Kötter, R.; Mayer, T.; Tüchler, M.; Schreckenbach, F.; Brauchle, J.: Channel Coding. Lecture notes, Institute for Communications Engineering, TU München, 2008.</ref>.}} | ||
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 5: Codes for satellites and space communications}$ | ||
| + | |||
| + | One of the first areas of application of error correction methods was communication from/to satellites and space shuttles, i.e. transmission routes characterized | ||
| + | *by low transmission powers | ||
| + | *and large path losses. | ||
| + | |||
| + | |||
| + | As early as 1977, channel coding was used in the space mission "Voyager 1" to Neptune and Uranus, in the form of serial concatenation of a [[Channel_Coding/Definition_und_Eigenschaften_von_Reed–Solomon–Codes|$\text{Reed–Solomon code}$]] and a [[Channel_Coding/Grundlagen_der_Faltungscodierung|$\text{convolutional code}$]].<br> | ||
| + | |||
| + | Thus, the power parameter $10 · \lg \; E_{\rm B}/N_0 \approx 2 \, \rm dB$ was already sufficient to achieve the required bit error rate $5 · 10^{-5}$ (related to the compressed data after source coding). Without channel coding, on the other hand, almost $9 \, \rm dB$ are required for the same bit error rate, i.e. a factor $10^{0.7} ≈ 5$ greater transmission power.<br> | ||
| + | |||
| + | The planned Mars project (data transmission from Mars to Earth with $\rm 5W$ lasers) will also only be successful with a sophisticated coding scheme.}}. | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 6: Channel codes for mobile communications}$ | ||
| + | |||
| + | A further and particularly high-turnover application area that would not function without channel coding is mobile communication. Here, unfavourable conditions without coding would result in error rates in the percentage range and, due to shadowing and multipath propagation (echoes), the errors often occur in bundles. The error bundle length is sometimes several hundred bits. | ||
| + | *For voice transmission in the [[Examples_of_Communication_Systems/Entire_GSM_Transmission_System|$\text{GSM system}$]], the $182$ most important (class 1a and 1b) of the total 260 bits of a voice frame $(20 \, \rm ms)$ together with a few parity and tailbits are convolutionally coded $($with memory $m = 4$ and code rate $R = 1/2)$ and scrambled. Together with the $78$ less important and therefore uncoded bits of class 2, this results in the bit rate increasing from $13 \, \rm kbit/s$ to $22.4 \, \rm kbit/s$ .<br> | ||
| + | |||
| + | *One uses the (relative) redundancy of $r = (22.4 - 13)/22.4 ≈ 0.42$ for error correction. It should be noted that $r = 0.42$ because of the definition used here, $42\%$ of the encoded bits are redundant. With the reference value "bit rate of the uncoded sequence" we would get $r = 9.4/13 \approx 0.72$ with the statement: To the information bits are added $72\%$ parity bits. <br> | ||
| + | |||
| + | *For [[Examples_of_Communication_Systems/Allgemeine_Beschreibung_von_UMTS|$\text{UMTS}$]] ("Universal Mobile Telecommunications System"), [[Channel_Coding/Grundlagen_der_Faltungscodierung|$\text{convolutional codes}$]] with the rates $R = 1/2$ or $R = 1/3$ are used. In the UMTS modes for higher data rates and correspondingly lower spreading factors, on the other hand, one uses [[Channel_Coding/Grundlegendes_zu_den_Turbocodes|$\text{Turbo codes}$]] of the rate $R = 1/3$ and iterative decoding. Depending on the number of iterations, gains of up to $3 \, \rm dB$ can be achieved compared to convolutional coding.}}<br> | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 7: Error protection of the compact disc}$ | ||
| + | |||
| + | For a compact disc $\rm (CD)$, one uses "cross-interleaved" [[Channel_Coding/Definition_und_Eigenschaften_von_Reed–Solomon–Codes|$\text{Reed–Solomon codes}$]] $\rm (RS)$ and then a so-called [https://en.wikipedia.org/wiki/Eight-to-fourteen_modulation $\text{Eight–to–Fourteen modulation}$]. Redundancy is used for error detection and correction. This coding scheme shows the following characteristics: | ||
| + | *The common code rate of the two RS–component codes is $R_{\rm RS} = 24/28 · 28/32 = 3/4$. Through the 8–to–14 modulation and some control bits, one arrives at the total code rate $R ≈ 1/3$.<br> | ||
| + | |||
| + | *In the case of statistically independent errors according to the [[Channel_Coding/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC|$\text{BSC}$]] model ("Binary Symmetric Channel"), a complete correction is possible as long as the bit error rate does not exceed the value $10^{-3}$.<br> | ||
| + | |||
| + | *The CD specific "Cross Interleaver" scrambles $108$ blocks together so that the $588$ bits of a block $($each bit corresponds to approx. $0.28 \, \rm {µ m})$ are distributed over approx. $1.75\, \rm cm$.<br> | ||
| − | == | + | *With the code rate $R ≈ 1/3$ one can correct approx. $10\%$ erasures. The lost values can be reconstructed (approximately) by interpolation ⇒ "Error Concealment".<br><br> |
| + | |||
| + | In summary, if a compact disc has a scratch of $1. 75\, \rm mm$ in length in the direction of play $($i.e. more than $6000$ consecutive erasures$)$, still $90\%$ of all the bits in a block are error-free, so that even the missing $10\%$ can be reconstructed, or at least the erasures can be disguised so that they are not audible.<br> | ||
| + | |||
| + | A demonstration of the CD's ability to correct follows in the next section.}}<br> | ||
| + | |||
| + | == The "Slit CD" - a demonstration by the LNT of TUM == | ||
<br> | <br> | ||
| − | + | At the end of the 1990s, members of the [https://www.ce.cit.tum.de/en/lnt/home/ $\text{Institute for Communications Engineering}$] of the [https://www.tum.de/en/about-tum/ $\text{Technical University of Munich}$] led by Prof. [[Biographies_and_Bibliographies/Lehrstuhlinhaber_des_LNT#Prof._Dr.-Ing._Dr.-Ing._E.h._Joachim_Hagenauer_.281993-2006.29|$\text{Joachim Hagenauer}$]] eliberately damaged a music–CD by cutting a total of three slits, each more than one millimetre wide. With each defect, almost $4000$ consecutive bits of audio coding are missing.<br> | |
| + | |||
| + | [[File:P ID2333 KC T 1 1 S2b.png|right|frame|"Slit CD" of the $\rm LNT/TUM$]] | ||
| + | |||
| + | The diagram shows the "slit CD": | ||
| + | *Both track 3 and track 14 have two such defective areas on each revolution. | ||
| + | |||
| + | *You can visualise the music quality with the help of the two audio players (playback time approx. 15 seconds each). | ||
| + | |||
| + | *The theory of this audio–demo can be found in the $\text{Example 7}$ in the previous section. <br> | ||
| + | |||
| − | + | Track 14: | |
| − | + | <lntmedia>file:A_ID59__14_1.mp3</lntmedia> | |
| − | + | Track 3: | |
| − | + | <lntmedia>file:A_ID60__3_1.mp3</lntmedia> | |
| − | + | <br><b>Summary of this audio demo:</b> | |
| + | *The CD's error correction is based on two serial–concatenated [[Channel_Coding/Definition_und_Eigenschaften_von_Reed–Solomon–Codes|$\text{Reed–Solomon codes}$]] and one [https://en.wikipedia.org/wiki/Eight-to-fourteen_modulation $\text{Eight–to–Fourteen modulation}$]. The total code rate for RS–error correction is $R = 3/4$.<br> | ||
| − | + | *As important for the functioning of the compact disc as the codes is the interposed interleaver, which distributes the erased bits ("erasures") over a length of almost $2 \, \rm cm$.<br> | |
| − | |||
| − | + | *In '''Track 14''' the two defective areas are sufficiently far apart. Therefore, the Reed–Solomon decoder is able to reconstruct the missing data.<br> | |
| − | + | *In '''Track 3''' the two error blocks follow each other in a very short distance, so that the correction algorithm fails. The result is an almost periodic clacking noise.<br><br> | |
| − | + | We would like to thank [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Dr.-Ing._Thomas_Hindelang_.28at_LNT_from_1994-2000_und_2007-2012.29|$\text{Thomas Hindelang}$]], Rainer Bauer, and Manfred Jürgens for the permission to use this audio–demo.<br> | |
| − | == | + | == Interplay between source and channel coding == |
<br> | <br> | ||
| − | '' | + | Transmission of natural sources such as speech, music, images, videos, etc. is usually done according to the discrete-time model outlined below. From [Liv10]<ref name ='Liv10'>Liva, G.: Channel Coding. Lectures manuscript, Institute for Communications Engineering, TU München and DLR Oberpfaffenhofen, 2010.</ref> the following should be noted: |
| + | *Source and sink are digitized and represented by (approximately equal numbers of) zeros and ones.<br> | ||
| + | |||
| + | *The source encoder compresses the binary data – in the following example a digital photo – and thus reduces the redundancy of the source.<br> | ||
| + | |||
| + | *The channel encoder adds redundancy again, and specifically so that some of the errors that occurred on the channel can be corrected in the channel decoder.<br> | ||
| + | |||
| + | *A discrete-time model with binary input and output is used here for the channel, which should also suitably take into account the components of the technical equipment at transmitter and receiver (modulator, decision device, clock recovery).<br><br> | ||
| + | |||
| + | With correct dimensioning of source and channel coding, the quality of the received photo is sufficiently good, even if the sink symbol sequence will not exactly match the source symbol sequence due to error patterns that cannot be corrected. One can also detect (red marked) bit errors within the sink symbol sequence of the next example.<br> | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
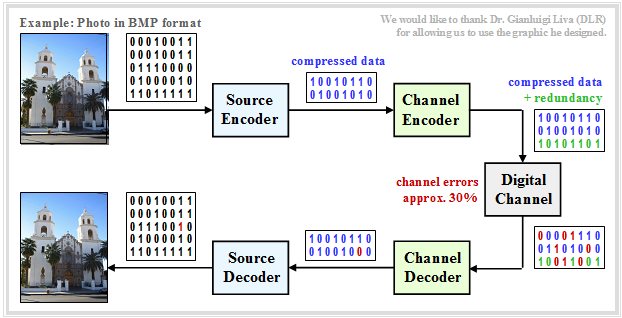
| + | $\text{Example 8:}$ For the graph, it was assumed, as an example and for the sake of simplicity, that | ||
| + | [[File:EN_KC_T_1_1_S3a_v3.png|right|frame|Image transmission with source and channel coding|class=fit]] | ||
| + | |||
| + | *the source symbol sequence has only the length $40$, | ||
| + | |||
| + | *the source encoder compresses the data by a factor of $40/16 = 2.5$, and | ||
| − | + | *the channel encoder adds $50\%$ redundancy. | |
| − | * | ||
| − | |||
| − | + | Thus, only $24$ encoder symbols have to be transmitted instead of $40$ source symbols, which reduces the overall transmission rate by $40\%$ .<br> | |
| − | + | If one were to dispense with source encoding by transmitting the original photo in BMP format rather than the compressed JPG image, the quality would be comparable, but a bit rate higher by a factor $2.5$ and thus much more effort would be required.}}<br> | |
| − | + | {{GraueBox|TEXT= | |
| − | + | [[File:EN_KC_T_1_1_S3b_v3.png|right|frame|Image transmission without source and channel coding|class=fit]] | |
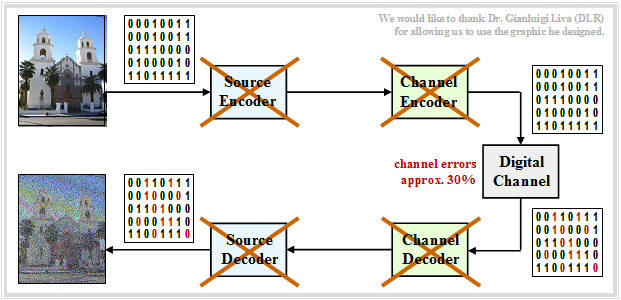
| + | $\text{Example 9:}$ | ||
| + | <br><br><br><br> | ||
| + | If one were to dispense with both, | ||
| + | *source coding and | ||
| + | *channel coding, | ||
| − | |||
| − | + | i.e. transmit the BMP data directly without error protection, the result would be extremely poor despite $($by a factor $40/24)$ greater bit rate. | |
| + | <br clear=all> | ||
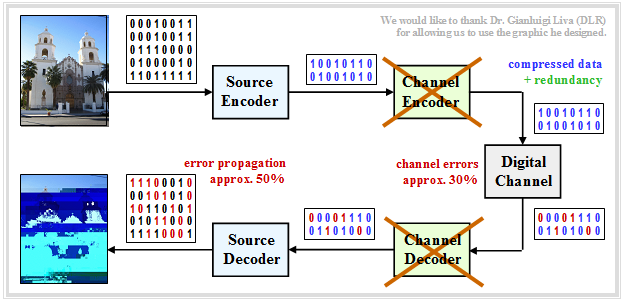
| + | [[File:EN_KC_T_1_1_S3c_v3.png|left|frame|Image transmission with source coding, but without channel coding|class=fit]] | ||
| + | <br><br> | ||
| + | »'''Source coding but no channel coding'''« | ||
| − | + | Now let's consider the case of directly transferring the compressed data (e.g. JPG) without error-proofing measures. Then: | |
| − | + | #The compressed source has only little redundancy left. | |
| + | #Thus, any single transmission error will cause entire blocks of images to be decoded incorrectly.<br> | ||
| + | #»'''This coding scheme should be avoided at all costs'''«.}}. | ||
| − | |||
| − | == | + | == Block diagram and requirements == |
<br> | <br> | ||
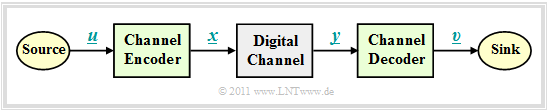
| − | + | In the further sections, we will start from the sketched block diagram with channel encoder, digital channel and channel decoder. The following conditions apply: | |
| + | |||
| + | [[File:EN_KC_T_1_1_S4_v2.png|right|frame|Block diagram describing channel coding|class=fit]] | ||
| + | |||
| + | *The vector $\underline{u} = (u_1, u_2, \text{...} \hspace{0.05cm}, u_k)$ denotes an »'''information block'''« with $k$ symbols. We restrict ourselves to binary symbols (bits) ⇒ $u_i \in \{0, \, 1\}$ for $i = 1, 2, \text{...} \hspace{0.05cm}, k$ with equal occurrence probabilities for zeros and ones.<br> | ||
| + | |||
| + | *Each information block $\underline{u}$ is represented by a »'''code word'''« (or "code block") $\underline{x} = (x_1, x_2, \text{. ..} \hspace{0.05cm}, x_n)$ with $n \ge k$, $x_i \in \{0, \, 1\}.$ One then speaks of a binary $(n, k)$ block code $C$. We denote the assignment by $\underline{x} = {\rm enc}(\underline{u})$, where "enc" stands for "encoder function".<br> | ||
| + | |||
| + | *The »'''received word'''« $\underline{y}$ results from the code word $\underline{x}$ by the [https://en.wikipedia.org/wiki/Modular_arithmetic $\text{modulo–2}$] sum with the likewise binary error vector $\underline{e} = (e_1, e_2, \text{. ..} \hspace{0.05cm}, e_n)$, where "$e= 1$" represents a transmission error and "$e= 0$" indicates that the $i$–th bit of the code word was transmitted correctly. The following therefore applies: | ||
| + | |||
| + | ::<math>\underline{y} = \underline{x} \oplus \underline{e} \hspace{0.05cm}, \hspace{0.5cm} y_i = x_i \oplus e_i \hspace{0.05cm}, \hspace{0.2cm} i = 1, \text{...} \hspace{0.05cm} , n\hspace{0.05cm}, </math> | ||
| + | ::<math>x_i \hspace{-0.05cm} \in \hspace{-0.05cm} \{ 0, 1 \}\hspace{0.05cm}, \hspace{0.5cm}e_i \in \{ 0, 1 \}\hspace{0.5cm} | ||
| + | \Rightarrow \hspace{0.5cm}y_i \in \{ 0, 1 \}\hspace{0.05cm}.</math> | ||
| + | *The description by the »'''digital channel model'''« – i.e. with binary input and output – is, however, only applicable if the transmission system makes hard decisions – see section [[Channel_Coding/Decoding_of_Linear_Block_Codes#Coding_gain_-_bit_error_rate_with_AWGN|"AWGN channel at binary input"]]. Systems with [[Channel_Coding/Decodierung_linearer_Blockcodes#Codiergewinn_.E2.80.93_Bitfehlerrate_bei_AWGN|$\text{soft decision}$]] cannot be modelled with this simple model.<br> | ||
| − | + | *The vector $\underline{v}$ after »'''channel decoding'''« has the same length $k$ as the information block $\underline{u}$. We describe the decoding process with the "decoder function" as $\underline{v} = {\rm enc}^{-1}(\underline{y}) = {\rm dec}(\underline{y})$. In the error-free case, analogous to $\underline{x} = {\rm enc}(\underline{u})$ ⇒ $\underline{v} = {\rm enc}^{-1}(\underline{y})$.<br> | |
| − | + | *If the error vector $\underline{e} \ne \underline{0}$, then $\underline{y}$ is usually not a valid element of the block code used, and the decoding is then not a pure mapping $\underline{y} \rightarrow \underline{v}$, but an estimate of $\underline{v}$ based on maximum match ("mimimum error probability").<br> | |
| − | + | == Important definitions for block coding == | |
| + | <br> | ||
| + | We now consider the exemplary binary block code | ||
| − | + | :<math>\mathcal{C} = \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 0, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 1, 1) \}\hspace{0.05cm}.</math> | |
| − | + | This code would be unsuitable for the purpose of error detection or error correction. But it is constructed in such a way that it clearly illustrates the calculation of important descriptive variables: | |
| − | * | + | *Here, each individual code word $\underline{u}$ is described by five bits. Throughout the book, we express this fact by the »'''code word length'''« $n = 5$. |
| − | * | + | *The above code contains four elements. Thus the »'''code size'''« $|C| = 4$. Accordingly, there are also four unique mappings between $\underline{u}$ and $\underline{x}$. |
| − | * | + | *The length of an information block $\underline{u}$ ⇒ »'''information block length'''« is denoted by $k$. Since for all binary codes $|C| = 2^k$ holds, it follows from $|C| = 4$ that $k = 2$. The assignments between $\underline{u}$ and $\underline{x}$ in the above code $C$ are: |
| − | + | ::<math>\underline{u_0} = (0, 0) \hspace{0.2cm}\leftrightarrow \hspace{0.2cm}(0, 0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm}, \hspace{0.8cm} | |
| + | \underline{u_1} = (0, 1) \hspace{0.2cm}\leftrightarrow \hspace{0.2cm}(0, 1, 0, 1, 0) = \underline{x_1}\hspace{0.05cm}, </math> | ||
| − | + | ::<math>\underline{u_2} = (1, 0)\hspace{0.2cm} \leftrightarrow \hspace{0.2cm}(1, 0, 1, 0, 1) = \underline{x_2}\hspace{0.05cm}, \hspace{0.8cm} | |
| + | \underline{u_3} = (1, 1) \hspace{0.2cm} \leftrightarrow \hspace{0.2cm}(1, 1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.</math> | ||
| + | *The code has the »'''code rate'''« $R = k/n = 2/5$. Accordingly, its redundancy is $1-R$, that is $60\%$. Without error protection $(n = k)$ the code rate $R = 1$.<br> | ||
| + | *A small code rate indicates that of the $n$ bits of a code word, very few actually carry information. A repetition code $(k = 1,\ n = 10)$ has the code rate $R = 0.1$.<br> | ||
| + | *The »'''Hamming weight'''« $w_{\rm H}(\underline{x})$ of the code word $\underline{x}$ indicates the number of code word elements $x_i \in \{0, \, 1\}$. For a binary code ⇒ $w_{\rm H}(\underline{x})$ is equal to the sum $x_1 + x_2 + \hspace{0.05cm}\text{...} \hspace{0.05cm}+ x_n$. In the example: | ||
| + | ::<math>w_{\rm H}(\underline{x}_0) = 0\hspace{0.05cm}, \hspace{0.4cm}w_{\rm H}(\underline{x}_1) = 2\hspace{0.05cm}, \hspace{0.4cm} w_{\rm H}(\underline{x}_2) = 3\hspace{0.05cm}, \hspace{0.4cm}w_{\rm H}(\underline{x}_3) = 5\hspace{0.05cm}. | ||
| + | </math> | ||
| + | *The »'''Hamming distance'''« $d_{\rm H}(\underline{x}, \ \underline{x}\hspace{0.03cm}')$ between the code words $\underline{x}$ and $\underline{x}\hspace{0.03cm}'$ denotes the number of bit positions in which the two code words differ: | ||
| + | ::<math>d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_1) = 2\hspace{0.05cm}, \hspace{0.4cm} | ||
| + | d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_2) = 3\hspace{0.05cm}, \hspace{0.4cm} | ||
| + | d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_3) = 5\hspace{0.05cm},\hspace{0.4cm} | ||
| + | d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_2) = 5\hspace{0.05cm}, \hspace{0.4cm} | ||
| + | d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_3) = 3\hspace{0.05cm}, \hspace{0.4cm} | ||
| + | d_{\rm H}(\underline{x}_2, \hspace{0.05cm}\underline{x}_3) = 2\hspace{0.05cm}.</math> | ||
| + | *An important property of a code $C$ that significantly affects its ability to be corrected is the »'''minimum distance'''« between any two code words: | ||
| + | ::<math>d_{\rm min}(\mathcal{C}) = | ||
| + | \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}')\hspace{0.05cm}.</math> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ A $(n, \hspace{0.05cm}k, \hspace{0.05cm}d_{\rm min})\text{ block code}$ has | ||
| + | *the code word length $n$, | ||
| + | *the information block length $k$ | ||
| + | *the minimum distance $d_{\rm min}$. | ||
| + | According to this nomenclature, the example considered here is a $(5, \hspace{0.05cm}2,\hspace{0.05cm} 2)$ block code. Sometimes one omits the specification of $d_{\rm min}$ ⇒ $(5,\hspace{0.05cm} 2)$ block code.}}<br> | ||
| + | == One example each of error detection and correction == | ||
| + | <br> | ||
| + | The variables just defined are now to be illustrated by two examples. | ||
| + | {{GraueBox|TEXT= | ||
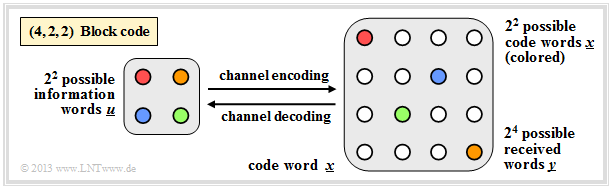
| + | $\text{Example 10:}$ $\text{(4, 2, 2) block code}$ | ||
| + | [[File:EN_KC_T_1_1_S5a_v3.png|right|frame|$\rm (4, 2, 2)$ block code for error detection|class=fit]] | ||
| + | In the graphic, the arrows | ||
| + | *pointing to the right illustrate the encoding process, | ||
| + | *pointing to the left illustrate the decoding process: | ||
| + | :$$\underline{u_0} = (0, 0) \leftrightarrow (0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm},$$ | ||
| + | :$$\underline{u_1} = (0, 1) \leftrightarrow (0, 1, 0, 1) = \underline{x_1}\hspace{0.05cm},$$ | ||
| + | :$$\underline{u_2} = (1, 0) \leftrightarrow (1, 0, 1, 0) = \underline{x_2}\hspace{0.05cm},$$ | ||
| + | :$$\underline{u_3} = (1, 1) \leftrightarrow (1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.$$ | ||
| + | On the right, all $2^4 = 16$ possible received words $\underline{y}$ are shown: | ||
| + | *Of these, $2^n - 2^k = 12$ can only be due to bit errors. | ||
| + | |||
| + | *If the decoder receives such a "white" code word, it detects an error, but it cannot correct it because $d_{\rm min} = 2$. | ||
| + | |||
| + | *For example, if $\underline{y} = (0, 0, 0, 1)$ is received, then with equal probability $\underline{x_0} = (0, 0, 0, 0)$ or $\underline{x_1} = (0, 1, 0, 1)$ may have been sent.}} | ||
| + | {{GraueBox|TEXT= | ||
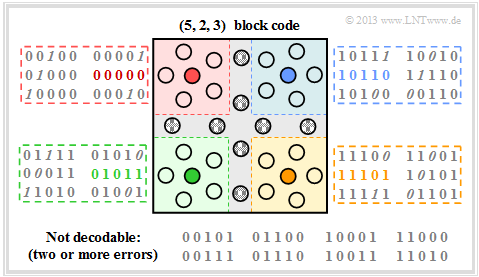
| + | $\text{Example 11:}$ $\text{(5, 2, 3) block code}$ | ||
| + | [[File:EN_KC_T_1_1_S54_v2.png|right|frame|$\rm (5, 2, 3)$ block code for error correction|class=fit]] | ||
| + | Here, because of $k=2$, there are again four valid code words: | ||
| + | :$$\underline{x_0} = (0, 0, 0, 0, 0)\hspace{0.05cm},\hspace{0.5cm} \underline{x_1} =(0, 1, 0, 1, 1)\hspace{0.05cm},$$ | ||
| + | :$$\underline{x_2} =(1, 0, 1, 1, 0)\hspace{0.05cm},\hspace{0.5cm}\underline{x_3} =(1, 1, 1, 0, 1).$$ | ||
| + | The graph shows the receiver side, where you can recognize falsified bits by the italics. | ||
| + | *Of the $2^n - 2^k = 28$ invalid code words, now $20$ can be assigned to a valid code word (fill colour: red, green, blue or ochre), assuming that a single bit error is more likely than their two or more. | ||
| + | |||
| + | *For each valid code word, there are five invalid code words, each with only one falsification ⇒ Hamming distance $d_{\rm H} =1$. These are indicated in the respective square with red, green, blue or ochre background colour. | ||
| + | |||
| + | *Error correction is possible for these due to the minimum distance $d_{\rm min} = 3$ between the code words. | ||
| + | |||
| + | *Eight received words are not decodable; the received word $\underline{y} = (0, 0, 1, 0, 1)$ could have arisen from the code word $\underline{x}_0 = (0, 0, 0, 0, 0)$ but also from the code word $\underline{x}_3 = (1, 1, 1, 0, 1)$. In both cases, two bit errors would have occurred.}}<br> | ||
| + | == On the nomenclature in this book == | ||
| + | <br> | ||
| + | One of the objectives of our learning tutorial $\rm LNTwww$ was to describe the entire field of Communications Engineering and the associated basic subjects with uniform nomenclature. In this most recently tackled book "Channel Coding" some changes have to be made with regard to the nomenclature after all. The reasons for this are: | ||
| + | *Coding theory is a largely self-contained subject and few authors of relevant reference books on the subject attempt to relate it to other aspects of digital signal transmission. | ||
| + | *The authors of the most important books on channel coding (English as well as German language) largely use a uniform nomenclature. We therefore do not take the liberty of squeezing the designations for channel coding into our communication technology scheme.<br> | ||
| + | Some nomenclature changes compared to the other $\rm LNTwww$ books shall be mentioned here: | ||
| + | #All signals are represented by sequences of symbols in vector notation. For example, $\underline{u} = (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$ is the "source symbol sequence and $\underline{v} = (v_1, v_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, v_k)$ the "sink symbol sequence". Previously, these symbol sequences were designated $\langle q_\nu \rangle$ and $\langle v_\nu \rangle$, respectively.<br><br> | ||
| + | #The vector $\underline{x} = (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n)$ now denotes the discrete-time equivalent to the transmitted signal $s(t)$, while the received signal $r(t)$ is described by the vector $\underline{y} = (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$ . The code rate is the quotient </i> $R=k/n$ with $0 \le R \le 1$ and the number of check bits is given by $m = n-k$.<br><br> | ||
| + | #In the first main chapter, the elements $u_i$ and $v_i$ $($each with index $i = 1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, k)$ of the vectors $\underline{u}$ and $\underline{v}$ are always binary $(0$ or $1)$, as are the $n$ elements $x_i$ of the code word $\underline{x}$. For digital channel model [[Channel_Coding/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC|$\text{(BSC}$]], [[Channel_Coding/Kanalmodelle_und_Entscheiderstrukturen#Binary_Erasure_Channel_.E2.80.93_BEC|$\text{BEC}$]], [[Channel_Coding/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Error_.26_Erasure_Channel_.E2.80.93_BSEC|$\text{BSEC})$]] this also applies to the $n$ received values $y_i \in \{0, 1\}$.<br><br> | ||
| + | #The [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_binary_input|$\text{AWGN}$]] channel is characterised by real-valued output values $y_i$. The "code word estimator" in this case extracts from the vector $\underline{y} = (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$ the binary vector $\underline{z} = (z_1, z_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, z_n)$ to be compared with the code word $\underline{x}$.<br><br> | ||
| + | #The transition from $\underline{y}$ to $\underline{z}$ is done by threshold decision ⇒ "Hard Decision" or according" to the MAP criterion ⇒ "Soft Decision". For equally likely input symbols, the "maximum Likelihood estimation also leads to the minimum error rate.<br><br> | ||
| + | #In the context of the AWGN model, it makes sense to represent binary code symbols $x_i$ bipolar (i.e. $\pm1$). This does not change the statistical properties. In the following, we mark bipolar signalling with a tilde. Then applies: | ||
| + | :::<math>\tilde{x}_i = 1 - 2 x_i = \left\{ \begin{array}{c} +1\\ | ||
| + | -1 \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} {\rm if} \hspace{0.15cm} x_i = 0\hspace{0.05cm},\\ | ||
| + | {\rm if} \hspace{0.15cm}x_i = 1\hspace{0.05cm}.\\ \end{array}</math> | ||
| + | == Exercises for the chapter == | ||
| + | <br> | ||
| + | [[Aufgaben:Exercise_1.1:_For_Labeling_Books|Exercise 1.1: For Labeling Books]] | ||
| + | [[Aufgaben:Exercise_1.2:_A_Simple_Binary_Channel_Code|Exercise 1.2: A Simple Binary Channel Code]] | ||
| + | |||
| + | [[Aufgaben:Exercise_1.2Z:_Three-dimensional_Representation_of_Codes|Exercise 1.2Z: Three-dimensional Representation of Codes]] | ||
| + | |||
| + | ==References== | ||
| − | |||
<references/> | <references/> | ||
| + | |||
| + | {{Display}} | ||
Latest revision as of 17:26, 18 November 2022
- [[Channel Coding/{{{Vorherige Seite}}} | Previous page]]
- [[Channel Coding/{{{Vorherige Seite}}} | Previous page]]
Contents
- 1 # OVERVIEW OF THE FIRST MAIN CHAPTER #
- 2 Error detection and error correction
- 3 Some introductory examples of error detection
- 4 Some introductory examples of error correction
- 5 The "Slit CD" - a demonstration by the LNT of TUM
- 6 Interplay between source and channel coding
- 7 Block diagram and requirements
- 8 Important definitions for block coding
- 9 One example each of error detection and correction
- 10 On the nomenclature in this book
- 11 Exercises for the chapter
- 12 References
# OVERVIEW OF THE FIRST MAIN CHAPTER #
The first chapter deals with »block codes for error detection and error correction« and provides the basics for describing more effective codes such as
- the »Reed-Solomon codes« (see Chapter 2),
- the »convolutional codes« (see Chapter 3), and
- the »iteratively decodable product codes« ("turbo codes") and the »low-density parity-check codes« (see Chapter 4).
This specific field of coding is called »Channel Coding« in contrast to
- »Source Coding« (redundancy reduction for reasons of data compression), and
- »Line Coding« (additional redundancy to adapt the digital signal to the spectral characteristics of the transmission medium).aa
We restrict ourselves here to »binary codes«. In detail, this book covers:
- Definitions and introductory examples of »error detection and error correction«,
- a brief review of appropriate »channel models« and »decision device structures«,
- known binary block codes such as »single parity-check code«, »repetition code« and »Hamming code«,
- the general description of linear codes using »generator matrix« and »check matrix«,
- the decoding possibilities for block codes, including »syndrome decoding« ,
- simple approximations and upper bounds for the »block error probability«, and
- an »information-theoretic bound« on channel coding.
Error detection and error correction
Transmission errors occur in every digital transmission system. It is possible to keep the probability $p_{\rm B}$ of such a bit error very small, for example by using a very large signal energy. However, the bit error probability $p_{\rm B} = 0$ is never achievable because of the Gaussian PDF of the thermal noise that is always present.
Particularly in the case of heavily disturbed channels and also for safety-critical applications, it is therefore essential to provide special protection for the data to be transmitted, adapted to the application and channel. For this purpose, redundancy is added at the transmitter and this redundancy is used at the receiver to reduce the number of decoding errors.
$\text{Definitions:}$
- »Error Detection«: The decoder checks the integrity of the received blocks and marks any errors found. If necessary, the receiver informs the transmitter about erroneous blocks via the return channel, so that the transmitter sends the corresponding block again.
- »Error Correction«: The decoder detects one (or more) bit errors and provides further information for them, for example their positions in the transmitted block. In this way, it may be possible to completely correct the errors that have occurred.
- »Channel Coding« includes both, procedures for »error detection« as well as those for »error correction«.
All $\rm ARQ$ ("Automatic Repeat Request") methods use error detection only.
- Less redundancy is required for error detection than for error correction.
- One disadvantage of ARQ is its low throughput when channel quality is poor, i.e. when entire blocks of data must be frequently re-requested by the receiver.
In this book we mostly deal with $\rm FEC$ ("Forward Error Correction") which leads to very small bit error rates if the channel is sufficiently good (large SNR).
- With worse channel conditions, nothing changes in the throughput, i.e. the same amount of information is transmitted.
- However, the symbol error rate can then assume very large values.
Often FEC and ARQ methods are combined, and the redundancy is divided between them in such a way,
- so that a small number of errors can still be corrected, but
- when there are too many errors, a repeat of the block is requested.
Some introductory examples of error detection
$\text{Example 1: Single Parity–Check Code $\rm (SPC)$}$
If one adds $k = 4$ bit by a so-called "parity bit" in such a way that the sum of all ones is even, e.g. (with bold parity bits)
- $$0000\hspace{0.03cm}\boldsymbol{0},\ 0001\hspace{0.03cm}\boldsymbol{1}, \text{...} ,\ 1111\hspace{0.03cm}\boldsymbol{0}, \text{...}\ ,$$
it is very easy to recognize a single error. Two errors within a code word, on the other hand, remain undetected.
$\text{Example 2: International Standard Book Number (ISBN)}$
Since the 1960s, all books have been given 10-digit codes ("ISBN–10"). Since 2007, the specification according to "ISBN–13" is additionally obligatory. For example, these are for the reference book [Söd93][1]:
- $\boldsymbol{3–540–57215–5}$ (for "ISBN–10"),
- $\boldsymbol{978–3–54057215–2}$ (for "ISBN–13").
The last digit $z_{10}$ for "ISBN–10" results from the previous digits $z_1 = 3$, $z_2 = 5$, ... , $z_9 = 5$ according to the following calculation rule:
- \[z_{10} = \left ( \sum_{i=1}^{9} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.3cm} \mod 11 = (1 \cdot 3 + 2 \cdot 5 + ... + 9 \cdot 5 ) \hspace{-0.2cm} \mod 11 = 5 \hspace{0.05cm}. \]
- Note that $z_{10} = 10$ must be written as $z_{10} = \rm X$ (roman numeral representation of "10"), since the number $10$ cannot be represented as a digit in the decimal system.
The same applies to the check digit for "ISBN–13":
- \[z_{13}= 10 - \left ( \sum_{i=1}^{12} \hspace{0.2cm} z_i \cdot 3^{(i+1) \hspace{-0.2cm} \mod 2} \right ) \hspace{-0.3cm} \mod 10 = 10 \hspace{-0.05cm}- \hspace{-0.05cm} \big [(9\hspace{-0.05cm}+\hspace{-0.05cm}8\hspace{-0.05cm}+\hspace{-0.05cm}5\hspace{-0.05cm}+\hspace{-0.05cm}0\hspace{-0.05cm}+\hspace{-0.05cm}7\hspace{-0.05cm}+\hspace{-0.05cm}1) \cdot 1 + (7\hspace{-0.05cm}+\hspace{-0.05cm}3\hspace{-0.05cm}+\hspace{-0.05cm}4\hspace{-0.05cm}+\hspace{-0.05cm}5\hspace{-0.05cm}+\hspace{-0.05cm}2\hspace{-0.05cm}+\hspace{-0.05cm}5) \cdot 3\big ] \hspace{-0.2cm} \mod 10 \]
- \[\Rightarrow \hspace{0.3cm} z_{13}= 10 - (108 \hspace{-0.2cm} \mod 10) = 10 - 8 = 2 \hspace{0.05cm}. \]
With both variants, in contrast to the above parity check code $\rm (SPC)$, number twists such as $57 \, \leftrightarrow 75$ are also recognized, since different positions are weighted differently here
.
$\text{Example 3: Bar code (one-dimensional)}$
The most widely used error-detecting code worldwide is the "bar code" for marking products, for example according to EAN–13 ("European Article Number") with 13 digits.
- These are represented by bars and gaps of different widths and can be easily decoded with an opto–electronic reader.
- The first three digits indicate the country (e.g. Germany: 400 ... 440), the next four or five digits producer and product.
- The last digit is the parity check digit $z_{13}$, which is calculated exactly as for ISBN–13.
Some introductory examples of error correction
$\text{Example 4: Two-dimensional bar codes for online tickets}$
If you book a railway ticket online and print it out, you will find an example of a two-dimensional bar code, namely the $\text{Aztec code}$ developed in 1995 by Andy Longacre at the Welch Allyn company in the USA, with which amounts of data up to $3000$ characters can be encoded. Due to the $\text{Reed–Solomon error correction}$, reconstruction of the data content is still possible even if up to $40\%$ of the code has been destroyed, for example by bending the ticket or by coffee stains.
On the right you see a $\rm QR\ code$ ("Quick Response") with associated content.
- The QR code was developed in 1994 for the automotive industry in Japan to mark components and also allows error correction.
- In the meantime, the use of the QR code has become very diverse. In Japan, it can be found on almost every advertising poster and on every business card. It has also been becoming more and more popular in Europe.
- All two-dimensional bar codes have square markings to calibrate the reader. You can find details on this in [KM+09][2].
$\text{Example 5: Codes for satellites and space communications}$
One of the first areas of application of error correction methods was communication from/to satellites and space shuttles, i.e. transmission routes characterized
- by low transmission powers
- and large path losses.
As early as 1977, channel coding was used in the space mission "Voyager 1" to Neptune and Uranus, in the form of serial concatenation of a $\text{Reed–Solomon code}$ and a $\text{convolutional code}$.
Thus, the power parameter $10 · \lg \; E_{\rm B}/N_0 \approx 2 \, \rm dB$ was already sufficient to achieve the required bit error rate $5 · 10^{-5}$ (related to the compressed data after source coding). Without channel coding, on the other hand, almost $9 \, \rm dB$ are required for the same bit error rate, i.e. a factor $10^{0.7} ≈ 5$ greater transmission power.
The planned Mars project (data transmission from Mars to Earth with $\rm 5W$ lasers) will also only be successful with a sophisticated coding scheme.
.
$\text{Example 6: Channel codes for mobile communications}$
A further and particularly high-turnover application area that would not function without channel coding is mobile communication. Here, unfavourable conditions without coding would result in error rates in the percentage range and, due to shadowing and multipath propagation (echoes), the errors often occur in bundles. The error bundle length is sometimes several hundred bits.
- For voice transmission in the $\text{GSM system}$, the $182$ most important (class 1a and 1b) of the total 260 bits of a voice frame $(20 \, \rm ms)$ together with a few parity and tailbits are convolutionally coded $($with memory $m = 4$ and code rate $R = 1/2)$ and scrambled. Together with the $78$ less important and therefore uncoded bits of class 2, this results in the bit rate increasing from $13 \, \rm kbit/s$ to $22.4 \, \rm kbit/s$ .
- One uses the (relative) redundancy of $r = (22.4 - 13)/22.4 ≈ 0.42$ for error correction. It should be noted that $r = 0.42$ because of the definition used here, $42\%$ of the encoded bits are redundant. With the reference value "bit rate of the uncoded sequence" we would get $r = 9.4/13 \approx 0.72$ with the statement: To the information bits are added $72\%$ parity bits.
- For $\text{UMTS}$ ("Universal Mobile Telecommunications System"), $\text{convolutional codes}$ with the rates $R = 1/2$ or $R = 1/3$ are used. In the UMTS modes for higher data rates and correspondingly lower spreading factors, on the other hand, one uses $\text{Turbo codes}$ of the rate $R = 1/3$ and iterative decoding. Depending on the number of iterations, gains of up to $3 \, \rm dB$ can be achieved compared to convolutional coding.
$\text{Example 7: Error protection of the compact disc}$
For a compact disc $\rm (CD)$, one uses "cross-interleaved" $\text{Reed–Solomon codes}$ $\rm (RS)$ and then a so-called $\text{Eight–to–Fourteen modulation}$. Redundancy is used for error detection and correction. This coding scheme shows the following characteristics:
- The common code rate of the two RS–component codes is $R_{\rm RS} = 24/28 · 28/32 = 3/4$. Through the 8–to–14 modulation and some control bits, one arrives at the total code rate $R ≈ 1/3$.
- In the case of statistically independent errors according to the $\text{BSC}$ model ("Binary Symmetric Channel"), a complete correction is possible as long as the bit error rate does not exceed the value $10^{-3}$.
- The CD specific "Cross Interleaver" scrambles $108$ blocks together so that the $588$ bits of a block $($each bit corresponds to approx. $0.28 \, \rm {µ m})$ are distributed over approx. $1.75\, \rm cm$.
- With the code rate $R ≈ 1/3$ one can correct approx. $10\%$ erasures. The lost values can be reconstructed (approximately) by interpolation ⇒ "Error Concealment".
In summary, if a compact disc has a scratch of $1. 75\, \rm mm$ in length in the direction of play $($i.e. more than $6000$ consecutive erasures$)$, still $90\%$ of all the bits in a block are error-free, so that even the missing $10\%$ can be reconstructed, or at least the erasures can be disguised so that they are not audible.
A demonstration of the CD's ability to correct follows in the next section.
The "Slit CD" - a demonstration by the LNT of TUM
At the end of the 1990s, members of the $\text{Institute for Communications Engineering}$ of the $\text{Technical University of Munich}$ led by Prof. $\text{Joachim Hagenauer}$ eliberately damaged a music–CD by cutting a total of three slits, each more than one millimetre wide. With each defect, almost $4000$ consecutive bits of audio coding are missing.
The diagram shows the "slit CD":
- Both track 3 and track 14 have two such defective areas on each revolution.
- You can visualise the music quality with the help of the two audio players (playback time approx. 15 seconds each).
- The theory of this audio–demo can be found in the $\text{Example 7}$ in the previous section.
Track 14:
Track 3:
Summary of this audio demo:
- The CD's error correction is based on two serial–concatenated $\text{Reed–Solomon codes}$ and one $\text{Eight–to–Fourteen modulation}$. The total code rate for RS–error correction is $R = 3/4$.
- As important for the functioning of the compact disc as the codes is the interposed interleaver, which distributes the erased bits ("erasures") over a length of almost $2 \, \rm cm$.
- In Track 14 the two defective areas are sufficiently far apart. Therefore, the Reed–Solomon decoder is able to reconstruct the missing data.
- In Track 3 the two error blocks follow each other in a very short distance, so that the correction algorithm fails. The result is an almost periodic clacking noise.
We would like to thank $\text{Thomas Hindelang}$, Rainer Bauer, and Manfred Jürgens for the permission to use this audio–demo.
Interplay between source and channel coding
Transmission of natural sources such as speech, music, images, videos, etc. is usually done according to the discrete-time model outlined below. From [Liv10][3] the following should be noted:
- Source and sink are digitized and represented by (approximately equal numbers of) zeros and ones.
- The source encoder compresses the binary data – in the following example a digital photo – and thus reduces the redundancy of the source.
- The channel encoder adds redundancy again, and specifically so that some of the errors that occurred on the channel can be corrected in the channel decoder.
- A discrete-time model with binary input and output is used here for the channel, which should also suitably take into account the components of the technical equipment at transmitter and receiver (modulator, decision device, clock recovery).
With correct dimensioning of source and channel coding, the quality of the received photo is sufficiently good, even if the sink symbol sequence will not exactly match the source symbol sequence due to error patterns that cannot be corrected. One can also detect (red marked) bit errors within the sink symbol sequence of the next example.
$\text{Example 8:}$ For the graph, it was assumed, as an example and for the sake of simplicity, that
- the source symbol sequence has only the length $40$,
- the source encoder compresses the data by a factor of $40/16 = 2.5$, and
- the channel encoder adds $50\%$ redundancy.
Thus, only $24$ encoder symbols have to be transmitted instead of $40$ source symbols, which reduces the overall transmission rate by $40\%$ .
If one were to dispense with source encoding by transmitting the original photo in BMP format rather than the compressed JPG image, the quality would be comparable, but a bit rate higher by a factor $2.5$ and thus much more effort would be required.
$\text{Example 9:}$
If one were to dispense with both,
- source coding and
- channel coding,
i.e. transmit the BMP data directly without error protection, the result would be extremely poor despite $($by a factor $40/24)$ greater bit rate.
»Source coding but no channel coding«
Now let's consider the case of directly transferring the compressed data (e.g. JPG) without error-proofing measures. Then:
- The compressed source has only little redundancy left.
- Thus, any single transmission error will cause entire blocks of images to be decoded incorrectly.
- »This coding scheme should be avoided at all costs«.
.
Block diagram and requirements
In the further sections, we will start from the sketched block diagram with channel encoder, digital channel and channel decoder. The following conditions apply:
- The vector $\underline{u} = (u_1, u_2, \text{...} \hspace{0.05cm}, u_k)$ denotes an »information block« with $k$ symbols. We restrict ourselves to binary symbols (bits) ⇒ $u_i \in \{0, \, 1\}$ for $i = 1, 2, \text{...} \hspace{0.05cm}, k$ with equal occurrence probabilities for zeros and ones.
- Each information block $\underline{u}$ is represented by a »code word« (or "code block") $\underline{x} = (x_1, x_2, \text{. ..} \hspace{0.05cm}, x_n)$ with $n \ge k$, $x_i \in \{0, \, 1\}.$ One then speaks of a binary $(n, k)$ block code $C$. We denote the assignment by $\underline{x} = {\rm enc}(\underline{u})$, where "enc" stands for "encoder function".
- The »received word« $\underline{y}$ results from the code word $\underline{x}$ by the $\text{modulo–2}$ sum with the likewise binary error vector $\underline{e} = (e_1, e_2, \text{. ..} \hspace{0.05cm}, e_n)$, where "$e= 1$" represents a transmission error and "$e= 0$" indicates that the $i$–th bit of the code word was transmitted correctly. The following therefore applies:
- \[\underline{y} = \underline{x} \oplus \underline{e} \hspace{0.05cm}, \hspace{0.5cm} y_i = x_i \oplus e_i \hspace{0.05cm}, \hspace{0.2cm} i = 1, \text{...} \hspace{0.05cm} , n\hspace{0.05cm}, \]
- \[x_i \hspace{-0.05cm} \in \hspace{-0.05cm} \{ 0, 1 \}\hspace{0.05cm}, \hspace{0.5cm}e_i \in \{ 0, 1 \}\hspace{0.5cm} \Rightarrow \hspace{0.5cm}y_i \in \{ 0, 1 \}\hspace{0.05cm}.\]
- The description by the »digital channel model« – i.e. with binary input and output – is, however, only applicable if the transmission system makes hard decisions – see section "AWGN channel at binary input". Systems with $\text{soft decision}$ cannot be modelled with this simple model.
- The vector $\underline{v}$ after »channel decoding« has the same length $k$ as the information block $\underline{u}$. We describe the decoding process with the "decoder function" as $\underline{v} = {\rm enc}^{-1}(\underline{y}) = {\rm dec}(\underline{y})$. In the error-free case, analogous to $\underline{x} = {\rm enc}(\underline{u})$ ⇒ $\underline{v} = {\rm enc}^{-1}(\underline{y})$.
- If the error vector $\underline{e} \ne \underline{0}$, then $\underline{y}$ is usually not a valid element of the block code used, and the decoding is then not a pure mapping $\underline{y} \rightarrow \underline{v}$, but an estimate of $\underline{v}$ based on maximum match ("mimimum error probability").
Important definitions for block coding
We now consider the exemplary binary block code
\[\mathcal{C} = \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 0, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 1, 1) \}\hspace{0.05cm}.\]
This code would be unsuitable for the purpose of error detection or error correction. But it is constructed in such a way that it clearly illustrates the calculation of important descriptive variables:
- Here, each individual code word $\underline{u}$ is described by five bits. Throughout the book, we express this fact by the »code word length« $n = 5$.
- The above code contains four elements. Thus the »code size« $|C| = 4$. Accordingly, there are also four unique mappings between $\underline{u}$ and $\underline{x}$.
- The length of an information block $\underline{u}$ ⇒ »information block length« is denoted by $k$. Since for all binary codes $|C| = 2^k$ holds, it follows from $|C| = 4$ that $k = 2$. The assignments between $\underline{u}$ and $\underline{x}$ in the above code $C$ are:
- \[\underline{u_0} = (0, 0) \hspace{0.2cm}\leftrightarrow \hspace{0.2cm}(0, 0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm}, \hspace{0.8cm} \underline{u_1} = (0, 1) \hspace{0.2cm}\leftrightarrow \hspace{0.2cm}(0, 1, 0, 1, 0) = \underline{x_1}\hspace{0.05cm}, \]
- \[\underline{u_2} = (1, 0)\hspace{0.2cm} \leftrightarrow \hspace{0.2cm}(1, 0, 1, 0, 1) = \underline{x_2}\hspace{0.05cm}, \hspace{0.8cm} \underline{u_3} = (1, 1) \hspace{0.2cm} \leftrightarrow \hspace{0.2cm}(1, 1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.\]
- The code has the »code rate« $R = k/n = 2/5$. Accordingly, its redundancy is $1-R$, that is $60\%$. Without error protection $(n = k)$ the code rate $R = 1$.
- A small code rate indicates that of the $n$ bits of a code word, very few actually carry information. A repetition code $(k = 1,\ n = 10)$ has the code rate $R = 0.1$.
- The »Hamming weight« $w_{\rm H}(\underline{x})$ of the code word $\underline{x}$ indicates the number of code word elements $x_i \in \{0, \, 1\}$. For a binary code ⇒ $w_{\rm H}(\underline{x})$ is equal to the sum $x_1 + x_2 + \hspace{0.05cm}\text{...} \hspace{0.05cm}+ x_n$. In the example:
- \[w_{\rm H}(\underline{x}_0) = 0\hspace{0.05cm}, \hspace{0.4cm}w_{\rm H}(\underline{x}_1) = 2\hspace{0.05cm}, \hspace{0.4cm} w_{\rm H}(\underline{x}_2) = 3\hspace{0.05cm}, \hspace{0.4cm}w_{\rm H}(\underline{x}_3) = 5\hspace{0.05cm}. \]
- The »Hamming distance« $d_{\rm H}(\underline{x}, \ \underline{x}\hspace{0.03cm}')$ between the code words $\underline{x}$ and $\underline{x}\hspace{0.03cm}'$ denotes the number of bit positions in which the two code words differ:
- \[d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_1) = 2\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_2) = 3\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_3) = 5\hspace{0.05cm},\hspace{0.4cm} d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_2) = 5\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_3) = 3\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_2, \hspace{0.05cm}\underline{x}_3) = 2\hspace{0.05cm}.\]
- An important property of a code $C$ that significantly affects its ability to be corrected is the »minimum distance« between any two code words:
- \[d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}')\hspace{0.05cm}.\]
$\text{Definition:}$ A $(n, \hspace{0.05cm}k, \hspace{0.05cm}d_{\rm min})\text{ block code}$ has
- the code word length $n$,
- the information block length $k$
- the minimum distance $d_{\rm min}$.
According to this nomenclature, the example considered here is a $(5, \hspace{0.05cm}2,\hspace{0.05cm} 2)$ block code. Sometimes one omits the specification of $d_{\rm min}$ ⇒ $(5,\hspace{0.05cm} 2)$ block code.
One example each of error detection and correction
The variables just defined are now to be illustrated by two examples.
$\text{Example 10:}$ $\text{(4, 2, 2) block code}$
In the graphic, the arrows
- pointing to the right illustrate the encoding process,
- pointing to the left illustrate the decoding process:
- $$\underline{u_0} = (0, 0) \leftrightarrow (0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm},$$
- $$\underline{u_1} = (0, 1) \leftrightarrow (0, 1, 0, 1) = \underline{x_1}\hspace{0.05cm},$$
- $$\underline{u_2} = (1, 0) \leftrightarrow (1, 0, 1, 0) = \underline{x_2}\hspace{0.05cm},$$
- $$\underline{u_3} = (1, 1) \leftrightarrow (1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.$$
On the right, all $2^4 = 16$ possible received words $\underline{y}$ are shown:
- Of these, $2^n - 2^k = 12$ can only be due to bit errors.
- If the decoder receives such a "white" code word, it detects an error, but it cannot correct it because $d_{\rm min} = 2$.
- For example, if $\underline{y} = (0, 0, 0, 1)$ is received, then with equal probability $\underline{x_0} = (0, 0, 0, 0)$ or $\underline{x_1} = (0, 1, 0, 1)$ may have been sent.
$\text{Example 11:}$ $\text{(5, 2, 3) block code}$
Here, because of $k=2$, there are again four valid code words:
- $$\underline{x_0} = (0, 0, 0, 0, 0)\hspace{0.05cm},\hspace{0.5cm} \underline{x_1} =(0, 1, 0, 1, 1)\hspace{0.05cm},$$
- $$\underline{x_2} =(1, 0, 1, 1, 0)\hspace{0.05cm},\hspace{0.5cm}\underline{x_3} =(1, 1, 1, 0, 1).$$
The graph shows the receiver side, where you can recognize falsified bits by the italics.
- Of the $2^n - 2^k = 28$ invalid code words, now $20$ can be assigned to a valid code word (fill colour: red, green, blue or ochre), assuming that a single bit error is more likely than their two or more.
- For each valid code word, there are five invalid code words, each with only one falsification ⇒ Hamming distance $d_{\rm H} =1$. These are indicated in the respective square with red, green, blue or ochre background colour.
- Error correction is possible for these due to the minimum distance $d_{\rm min} = 3$ between the code words.
- Eight received words are not decodable; the received word $\underline{y} = (0, 0, 1, 0, 1)$ could have arisen from the code word $\underline{x}_0 = (0, 0, 0, 0, 0)$ but also from the code word $\underline{x}_3 = (1, 1, 1, 0, 1)$. In both cases, two bit errors would have occurred.
On the nomenclature in this book
One of the objectives of our learning tutorial $\rm LNTwww$ was to describe the entire field of Communications Engineering and the associated basic subjects with uniform nomenclature. In this most recently tackled book "Channel Coding" some changes have to be made with regard to the nomenclature after all. The reasons for this are:
- Coding theory is a largely self-contained subject and few authors of relevant reference books on the subject attempt to relate it to other aspects of digital signal transmission.
- The authors of the most important books on channel coding (English as well as German language) largely use a uniform nomenclature. We therefore do not take the liberty of squeezing the designations for channel coding into our communication technology scheme.
Some nomenclature changes compared to the other $\rm LNTwww$ books shall be mentioned here:
- All signals are represented by sequences of symbols in vector notation. For example, $\underline{u} = (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$ is the "source symbol sequence and $\underline{v} = (v_1, v_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, v_k)$ the "sink symbol sequence". Previously, these symbol sequences were designated $\langle q_\nu \rangle$ and $\langle v_\nu \rangle$, respectively.
- The vector $\underline{x} = (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n)$ now denotes the discrete-time equivalent to the transmitted signal $s(t)$, while the received signal $r(t)$ is described by the vector $\underline{y} = (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$ . The code rate is the quotient $R=k/n$ with $0 \le R \le 1$ and the number of check bits is given by $m = n-k$.
- In the first main chapter, the elements $u_i$ and $v_i$ $($each with index $i = 1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, k)$ of the vectors $\underline{u}$ and $\underline{v}$ are always binary $(0$ or $1)$, as are the $n$ elements $x_i$ of the code word $\underline{x}$. For digital channel model $\text{(BSC}$, $\text{BEC}$, $\text{BSEC})$ this also applies to the $n$ received values $y_i \in \{0, 1\}$.
- The $\text{AWGN}$ channel is characterised by real-valued output values $y_i$. The "code word estimator" in this case extracts from the vector $\underline{y} = (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$ the binary vector $\underline{z} = (z_1, z_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, z_n)$ to be compared with the code word $\underline{x}$.
- The transition from $\underline{y}$ to $\underline{z}$ is done by threshold decision ⇒ "Hard Decision" or according" to the MAP criterion ⇒ "Soft Decision". For equally likely input symbols, the "maximum Likelihood estimation also leads to the minimum error rate.
- In the context of the AWGN model, it makes sense to represent binary code symbols $x_i$ bipolar (i.e. $\pm1$). This does not change the statistical properties. In the following, we mark bipolar signalling with a tilde. Then applies:
- \[\tilde{x}_i = 1 - 2 x_i = \left\{ \begin{array}{c} +1\\ -1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm if} \hspace{0.15cm} x_i = 0\hspace{0.05cm},\\ {\rm if} \hspace{0.15cm}x_i = 1\hspace{0.05cm}.\\ \end{array}\]
Exercises for the chapter
Exercise 1.1: For Labeling Books
Exercise 1.2: A Simple Binary Channel Code
Exercise 1.2Z: Three-dimensional Representation of Codes
References
- ↑ Söder, G.: Modellierung, Simulation und Optimierung von Nachrichtensystemen. Berlin - Heidelberg: Springer, 1993.
- ↑ Kötter, R.; Mayer, T.; Tüchler, M.; Schreckenbach, F.; Brauchle, J.: Channel Coding. Lecture notes, Institute for Communications Engineering, TU München, 2008.
- ↑ Liva, G.: Channel Coding. Lectures manuscript, Institute for Communications Engineering, TU München and DLR Oberpfaffenhofen, 2010.