Difference between revisions of "Modulation Methods/Quality Criteria"
| Line 94: | Line 94: | ||
*Lineare Verzerrungen können im Allgemeinen durch einen Entzerrer kompensiert werden, was allerdings bei Vorhandensein einer stochastischen Störung $n(t)$ stets zu einer höheren Störleistung und damit zu einem geringeren Sinken–SNR führt. | *Lineare Verzerrungen können im Allgemeinen durch einen Entzerrer kompensiert werden, was allerdings bei Vorhandensein einer stochastischen Störung $n(t)$ stets zu einer höheren Störleistung und damit zu einem geringeren Sinken–SNR führt. | ||
*Lineare Verzerrungen werden weiter in ''Dämpfungsverzerrungen'' und ''Phasenverzerrungen'' unterteilt. | *Lineare Verzerrungen werden weiter in ''Dämpfungsverzerrungen'' und ''Phasenverzerrungen'' unterteilt. | ||
| + | |||
| + | |||
'''Nichtlineare Verzerrungen''' entsprechend der Beschreibung im [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen|gleichnamigen Kapitel]] des Buches „Lineare zeitinvariante Systeme”. | '''Nichtlineare Verzerrungen''' entsprechend der Beschreibung im [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen|gleichnamigen Kapitel]] des Buches „Lineare zeitinvariante Systeme”. | ||
*Nichtlineare Verzerrungen sind irreversibel und damit eine stärkere Beeinträchtigung als lineare Verzerrungen. | *Nichtlineare Verzerrungen sind irreversibel und damit eine stärkere Beeinträchtigung als lineare Verzerrungen. | ||
| Line 105: | Line 107: | ||
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT=Anzumerken ist, dass die Verzerrungen bezüglich $q(t)$ und $υ(t)$ stets dann von nichtlinearer Art sind, wenn der Kanal nichtlineare Komponenten beinhaltet und damit bereits nichtlineare Verzerrungen bezüglich der Signale $s(t)$ und $r(t)$ gegeben sind. Ebenso führen Nichtlinearitäten bei Modulator und Demodulator stets zu nichtlinearen Verzerrungen.}} |
| Line 111: | Line 113: | ||
==Einige Anmerkungen zum AWGN–Kanalmodell== | ==Einige Anmerkungen zum AWGN–Kanalmodell== | ||
| − | Zur Untersuchung des Rauschverhaltens der einzelnen Modulations– und Demodulationsverfahren gehen wir meist vom so genannten AWGN–Kanal aus, wobei die Abkürzung für Additive White Gaussian Noise steht und die Eigenschaften dieses Kanalmodells bereits hinreichend beschreibt: | + | Zur Untersuchung des Rauschverhaltens der einzelnen Modulations– und Demodulationsverfahren gehen wir meist vom so genannten '''AWGN–Kanal''' aus, wobei die Abkürzung für ''Additive White Gaussian Noise'' steht und die Eigenschaften dieses Kanalmodells bereits hinreichend beschreibt. Wir weisen Sie hier gerne auch auf das dreiteilige Lernvideo [[Der_AWGN-Kanal_(Lernvideo)|Der AWGN-Kanal]] hin: |
| − | |||
*Das additive Störsignal beinhaltet alle Frequenzanteile gleichermaßen; $n(t)$ besitzt ein konstantes Leistungsdichtespektrum (LDS) und eine diracförmige Autokorrelationsfunktion (AKF): | *Das additive Störsignal beinhaltet alle Frequenzanteile gleichermaßen; $n(t)$ besitzt ein konstantes Leistungsdichtespektrum (LDS) und eine diracförmige Autokorrelationsfunktion (AKF): | ||
| − | $${\it \Phi}_n(f) = \frac{N_0}{2}\hspace{0.15cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, | + | :$${\it \Phi}_n(f) = \frac{N_0}{2}\hspace{0.15cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, |
\hspace{0.15cm} \varphi_n(\tau) = \frac{N_0}{2} \cdot \delta (\tau)\hspace{0.05cm}.$$ | \hspace{0.15cm} \varphi_n(\tau) = \frac{N_0}{2} \cdot \delta (\tau)\hspace{0.05cm}.$$ | ||
| − | :Der Faktor 1/2 in diesen Gleichungen berücksichtigt jeweils die zweiseitige Spektraldarstellung. | + | :Der Faktor $1/2$ in diesen Gleichungen berücksichtigt jeweils die zweiseitige Spektraldarstellung. |
| − | + | *Beispielsweise gilt bei thermischem Rauschen für die physikalische Rauschleistungsdichte (das heißt: einseitige Betrachtungsweise) mit der Rauschzahl $F ≥ 1$ und der absoluten Temperatur $θ$: | |
| − | + | :$${N_0}= F \cdot k_{\rm B} \cdot \theta , \hspace{0.3cm}k_{\rm B} = | |
| − | *Beispielsweise gilt bei thermischem Rauschen für die physikalische Rauschleistungsdichte (das heißt: einseitige Betrachtungsweise) mit der Rauschzahl $F | ||
| − | $${N_0}= F \cdot k_{\rm B} \cdot \theta , \hspace{0.3cm}k_{\rm B} = | ||
1.38 \cdot 10^{-23}{ {\rm Ws} }/{ {\rm K} }\hspace{0.2cm}{\rm | 1.38 \cdot 10^{-23}{ {\rm Ws} }/{ {\rm K} }\hspace{0.2cm}{\rm | ||
(Boltzmann-Konstante)}\hspace{0.05cm}.$$ | (Boltzmann-Konstante)}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
*Bei echt weißem Rauschen würde sich eine unendliche große Leistung ergeben. Deshalb ist stets eine Bandbegrenzung auf $B$ zu berücksichtigen, und es gilt für die wirksame Rauschleistung: | *Bei echt weißem Rauschen würde sich eine unendliche große Leistung ergeben. Deshalb ist stets eine Bandbegrenzung auf $B$ zu berücksichtigen, und es gilt für die wirksame Rauschleistung: | ||
| − | $$N = \sigma_n^2 = {N_0} \cdot B \hspace{0.05cm}.$$ | + | :$$N = \sigma_n^2 = {N_0} \cdot B \hspace{0.05cm}.$$ |
| − | |||
| − | |||
*Die Amplitude $n$ des Störsignals besitzt eine Gaußsche Wahrscheinlichkeitsdichtefunktion (WDF) mit dem Störeffektivwert $σ_n$: | *Die Amplitude $n$ des Störsignals besitzt eine Gaußsche Wahrscheinlichkeitsdichtefunktion (WDF) mit dem Störeffektivwert $σ_n$: | ||
| − | $$f_n(n) = \frac{1}{\sqrt{2\pi}\cdot\sigma_n}\cdot {\rm e}^{-{\it | + | :$$f_n(n) = \frac{1}{\sqrt{2\pi}\cdot\sigma_n}\cdot {\rm e}^{-{\it |
n^{\rm 2}}/{(2\sigma_{\it n}^2)}}.$$ | n^{\rm 2}}/{(2\sigma_{\it n}^2)}}.$$ | ||
| − | + | *Eigentlich ist beim AWGN–Kanal $H_{\rm K}(f) = 1$ zu setzen. Wir modifizieren dieses Modell für unsere Untersuchungen jedoch in der Form, dass wir eine frequenzunabhängige Dämpfung zulassen: | |
| − | + | :$$H_{\rm K}(f) = \alpha_{\rm K}= {\rm const.}$$ | |
| − | *Eigentlich ist beim AWGN–Kanal $H_{\rm K}(f) =$ | ||
| − | $$H_{\rm K}(f) = \alpha_{\rm K}= {\rm const.}$$ | ||
:Ein solcher frequenzunabhängiger Dämpfungsfaktor führt nicht zu Verzerrungen. | :Ein solcher frequenzunabhängiger Dämpfungsfaktor führt nicht zu Verzerrungen. | ||
| − | + | ==Untersuchungen beim AWGN–Kanal== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ==Untersuchungen beim AWGN–Kanal | ||
Bei allen Untersuchungen hinsichtlich des Rauschverhaltens gehen wir von folgendem Blockschaltbild aus: | Bei allen Untersuchungen hinsichtlich des Rauschverhaltens gehen wir von folgendem Blockschaltbild aus: | ||
| + | [[File: P_ID945__Mod_T_1_2_S5_neu.png |center|frame| Blockschaltbild zur Untersuchung des Rauschverhaltens]] | ||
| − | + | Wir werden dabei stets das Sinken–SNR $ρ_v$ in Abhängigkeit aller Systemparameter berechnen und zu folgenden Ergebnissen kommen: | |
| + | *Je mehr Sendeleistung $P_{\rm S}$ aufgewendet wird, desto besser ist das Sinken–SNR $ρ_v$. Bei einigen Verfahren ergibt sich sogar ein linearer Zusammenhang. | ||
| + | *Dagegen nimmt $ρ_v$ mit steigender Rauschleistungsdichte $N_0$ monoton ab. Eine Vergrößerung von $N_0$ kann meist durch eine größere Sendeleistung $P_{\rm S}$ ausgeglichen werden. | ||
| + | *Je kleiner der Dämpfungsfaktor $α_{\rm K}$ ist – das heißt, je stärker der Kanal dämpft – um so kleiner wird $ρ_v$. Es besteht oft eine quadratische Abhängigkeit, da die Empfangsleistung $P_{\rm E} = {α_{\rm K}}^2 · P_{\rm S}$ ist. | ||
| + | *Auch ein breitbandigeres Quellensignal (größeres $B_{\rm NF}$) führt zu einem kleineren $ρ_v$, da dadurch auch die HF–Bandbreite vergrößert werden muss und somit mehr Störungen wirksam werden. | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | '''Resümee:''' Unter Berücksichtigung dieser vier Aussagen kommt man zu dem Schluss, dass es Sinn macht, das Sinken–SNR in der Form | |
| − | + | :$$\rho_{v } = \rho_{v }(\xi) \hspace{0.5cm} {\rm mit} \hspace{0.5cm}\xi = \frac{ {\alpha_{\rm K} }^2 \cdot P_{\rm S} }{{N_0} \cdot B_{\rm NF} }$$ | |
| − | |||
| − | |||
| + | normiert darzustellen. Die in $ξ$ zusammengefassten Eingangsgrößen sind in obigem Bild mit blauen Pfeilen markiert, während das Qualitätskriterium $ρ_υ$ durch den roten Pfeil hervorgehoben ist.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
{{Beispiel}} | {{Beispiel}} | ||
In der linken Grafik ist das Sinken–SNR $ρ_υ$ für drei verschiedene Systeme dargestellt, jeweils in Abhängigkeit von der normierten Leistungskenngröße | In der linken Grafik ist das Sinken–SNR $ρ_υ$ für drei verschiedene Systeme dargestellt, jeweils in Abhängigkeit von der normierten Leistungskenngröße | ||
Revision as of 08:30, 19 June 2017
Contents
Ideales und verzerrungsfreies System
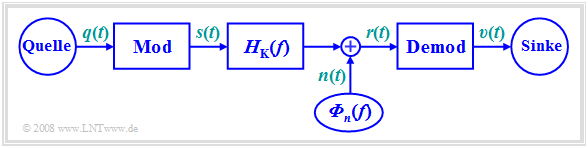
In allen nachfolgenden Kapiteln wird stets von folgendem Modell ausgegangen:
Die Aufgabe eines jeden Nachrichtenübertragungssystems besteht darin, an der räumlich entfernten Sinke ein Signal $v(t)$ zur Verfügung zu stellen, das sich möglichst wenig vom Quellensignal $q(t)$ unterscheidet.
Definition: Ein ideales System liegt vor, wenn folgende Bedingung erfüllt ist:
- $$v(t) = q(t) + n(t), \hspace{1cm}n(t) \to 0.$$
Hierbei ist berücksichtigt, dass $n(t) \equiv 0$ aus physikalischen Gründen aufgrund des Thermischen Rauschens nicht möglich ist.
In der Praxis werden sich die Signale $q(t)$ und $v(t)$ nicht nur um $n(t)$ unterscheiden, wofür es folgende Gründe gibt:
- Nichtideale Realisierung von Modulator und Demodulator,
- lineare Dämpfungs– und Phasenverzerrungen sowie Nichtlinearitäten,
- externe Störungen und zusätzliche stochastische Rauschprozesse,
- frequenzunabhängige Dämpfung und Laufzeit.
Definition: Ein verzerrungsfreies System liegt vor, wenn von dieser Auflistung nur die letztgenannte Einschränkung wirksam ist:
- $$v(t) = \alpha \cdot q(t- \tau) + n(t), \hspace{1cm}n(t) \to 0.$$
- Durch den Dämpfungsfaktor $α$ ist das Sinkensignal $υ(t)$ gegenüber dem Quellensignal $q(t)$ nur „leiser”.
- Auch eine Laufzeit $τ$ ist oft tolerabel, zumindest bei einer unidirektionalen Übertragung.
- Dagegen wird bei einer bidirektionalen Kommunikation – zum Beispiel einem Telefonat – schon eine Laufzeit von 300 Millisekunden als sehr störend empfunden.
Signal–zu–Stör–Leistungsverhältnis
Im allgemeinen Fall wird sich das Sinkensignal $v(t)$ auch gegenüber $α · q(t – τ)$ unterscheiden, und es gilt für das Fehlersignal:
- $$\varepsilon (t) = v(t) - \alpha \cdot q(t- \tau) = \varepsilon_{\rm V} (t) + \varepsilon_{\rm St} (t).$$
Dieses Fehlersignal setzt sich aus zwei Anteilen zusammen:
- den linearen und nichtlinearen Verzerrungen $ε_{\rm V}(t)$, die durch Modulator, Kanal und Demodulator hervorgerufen werden können und deterministisches Verhalten zeigen,
- der stochastischen Komponente $ε_{\rm St}(t)$, die von der HF–Störung $n(t)$ am Demodulatoreingang herrührt. Im Gegensatz zu $n(t)$ handelt es sich bei $ε_{\rm St}(t)$ jedoch um eine niederfrequente Störung.
Definition: Als Maß für die Qualität des Nachrichtensystems wird das Signal–zu–Stör–Leistungsverhältnis $ρ_v$ an der Sinke als Quotient der Leistungen (Varianzen) von Nutzanteil $υ(t) – ε(t)$ und Störanteil $ε(t)$ definiert:
- $$P_{v -\varepsilon} = \overline{[v(t)-\varepsilon(t)]^2} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M} } \cdot \int_{0}^{ T_{\rm M} } {[v(t)-\varepsilon(t)]^2 }\hspace{0.1cm}{\rm d}t,\hspace{0.5cm} P_{\varepsilon} = \overline{\varepsilon^2(t)} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M} } \cdot \int_{0}^{ T_{\rm M} } {\varepsilon^2(t) }\hspace{0.1cm}{\rm d}t$$
- $$\Rightarrow \hspace{0.5cm}\rho_{v} = \frac{ P_{v -\varepsilon} }{P_{\varepsilon} } \hspace{0.05cm}.$$
Für die Leistung des Nutzanteils erhält man unabhängig von der Laufzeit $τ$:
- $$P_{v -\varepsilon} = \overline{[v(t)-\varepsilon(t)]^2} = \overline{\alpha^2 \cdot q^2(t - \tau)}= \alpha^2 \cdot P_{q}.$$
Hierbei bezeichnet $P_q$ die Leistung des Quellensignals $q(t)$:
- $$P_{q} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {q^2(t) }\hspace{0.1cm}{\rm d}t .$$
Damit erhält man:
- $$\rho_{v} = \frac{\alpha^2 \cdot P_{q} }{P_{\varepsilon} } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho_{v} = 10 \cdot {\rm lg} \hspace{0.15cm} \frac{\alpha^2 \cdot P_{q} }{P_{\varepsilon} } \hspace{0.05cm}.$$
Im Folgenden bezeichnen wir $ρ_v$ kurz als das Signal–to–Noise–Ratio (oder kurz Sinken–SNR) und 10 · lg $ρ_v$ als den Sinken–Störabstand, der bei Verwendung des Zehner–Logarithmus (lg) in dB angegeben wird.
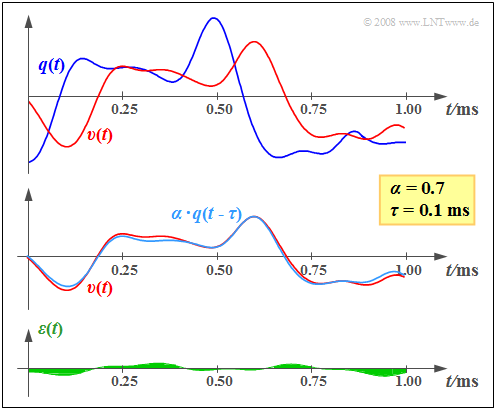
Beispiel 1: Oben sind beispielhafte Ausschnitte
- des (blauen) Quellensignals $q(t)$ und
- des (roten) Sinkensignals $v(t)$,
dargestellt, die sich deutlich voneinander unterscheiden.
Die mittlere Grafik macht jedoch deutlich, dass der wesentliche Unterschied zwischen $q(t)$ und $v(t)$ auf den Dämpfungsfaktor $α = 0.7$ und die Laufzeit $τ = 0.1$ Millisekunden zurückzuführen ist.
Die untere Skizze zeigt das verbleibende Fehlersignal $ε(t) = v(t) – α · q(t – τ)$ nach Korrektur von Dämpfung und Laufzeit. Den quadratischen Mittelwert (Varianz) dieses Signals bezeichnen wir als die Störleistung $P_ε$.
Zur Berechnung des Sinken–SNR $ρ_v$ muss $P_ε$ in Bezug zur Nutzleistung $α^2 · P_q$ gesetzt werden. Diese ergibt sich als die Varianz des in der mittleren Grafik hellblau eingezeichneten Signals $α · q(t – τ)$.
Mit den hier vorausgesetzten Kenngrößen $\alpha = 0.7$ ⇒ $\alpha^2 \approx 0.5$ sowie $P_{q} = 8\,{\rm V^2}$ und ${P_{\varepsilon} } = 0.04\,{\rm V^2}$ ergibt sich das Sinken–SNR $ρ_v ≈ 100$ bzw. der Sinken–Störabstand $10 · \lg ρ_v ≈ 20$ dB.
Das Fehlersignal $ε(t)$ – und damit auch das Sinken–SNR $ρ_v$ – berücksichtigt alle Unzulänglichkeiten des betrachteten Nachrichtenübertragungssystems (Verzerrungen, externe Störungen, Rauschen, usw.). Im Folgenden werden wir aus Darstellungsgründen die unterschiedlichen Effekte getrennt betrachten.
Untersuchungen im Hinblick auf Signalverzerrungen
Alle in den folgenden Kapiteln beschriebenen Modulationsverfahren führen bei nichtidealen Bedingungen zu Verzerrungen, das heißt zu einem Sinkensignal $v(t) ≠ α · q(t – τ)$, das sich nicht nur durch eine Dämpfung und eine Laufzeit von $q(t)$ unterscheidet. Für die Untersuchung und Beschreibung dieser Signalverfälschungen gehen wir stets von folgenden Voraussetzungen und folgendem Modell aus:
- Das additive Störsignal $n(t)$ am Kanalausgang (Demodulatoreingang) sei vernachlässigbar klein und wird nicht berücksichtigt.
- Alle Komponenten von Modulator und Demodulator seien linear, ebenso wie der Kanal, der somit durch seinen Frequenzgang $H_{\rm K}(f)$ vollständig beschrieben wird.
Je nach Art und Realisierung von Modulator und Demodulator treten folgende Signalverfälschungen auf:
Lineare Verzerrungen entsprechend der Beschreibung im gleichnamigen Kapitel des Buches „Lineare zeitinvariante Systeme”.
- Lineare Verzerrungen können im Allgemeinen durch einen Entzerrer kompensiert werden, was allerdings bei Vorhandensein einer stochastischen Störung $n(t)$ stets zu einer höheren Störleistung und damit zu einem geringeren Sinken–SNR führt.
- Lineare Verzerrungen werden weiter in Dämpfungsverzerrungen und Phasenverzerrungen unterteilt.
Nichtlineare Verzerrungen entsprechend der Beschreibung im gleichnamigen Kapitel des Buches „Lineare zeitinvariante Systeme”.
- Nichtlineare Verzerrungen sind irreversibel und damit eine stärkere Beeinträchtigung als lineare Verzerrungen.
- Zur quantitativen Erfassung solcher Verzerrungen eignet sich beispielsweise der Klirrfaktor $K$, der mit dem Sinken–SNR in folgendem Zusammenhang steht: $\rho_{v} = {1}/{K^2} \hspace{0.05cm}.$
- Die Angabe des Klirrfaktors setzt jedoch eine harmonische Schwingung als Quellensignal voraus.
Wir verweisen hier auf drei grundlegende Lernvideos:
- Lineare und nichtlineare Verzerrungen
- Eigenschaften des Übertragungskanals
- Einige Anmerkungen zur Übertragungsfunktion
Anzumerken ist, dass die Verzerrungen bezüglich $q(t)$ und $υ(t)$ stets dann von nichtlinearer Art sind, wenn der Kanal nichtlineare Komponenten beinhaltet und damit bereits nichtlineare Verzerrungen bezüglich der Signale $s(t)$ und $r(t)$ gegeben sind. Ebenso führen Nichtlinearitäten bei Modulator und Demodulator stets zu nichtlinearen Verzerrungen.
Einige Anmerkungen zum AWGN–Kanalmodell
Zur Untersuchung des Rauschverhaltens der einzelnen Modulations– und Demodulationsverfahren gehen wir meist vom so genannten AWGN–Kanal aus, wobei die Abkürzung für Additive White Gaussian Noise steht und die Eigenschaften dieses Kanalmodells bereits hinreichend beschreibt. Wir weisen Sie hier gerne auch auf das dreiteilige Lernvideo Der AWGN-Kanal hin:
- Das additive Störsignal beinhaltet alle Frequenzanteile gleichermaßen; $n(t)$ besitzt ein konstantes Leistungsdichtespektrum (LDS) und eine diracförmige Autokorrelationsfunktion (AKF):
- $${\it \Phi}_n(f) = \frac{N_0}{2}\hspace{0.15cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.15cm} \varphi_n(\tau) = \frac{N_0}{2} \cdot \delta (\tau)\hspace{0.05cm}.$$
- Der Faktor $1/2$ in diesen Gleichungen berücksichtigt jeweils die zweiseitige Spektraldarstellung.
- Beispielsweise gilt bei thermischem Rauschen für die physikalische Rauschleistungsdichte (das heißt: einseitige Betrachtungsweise) mit der Rauschzahl $F ≥ 1$ und der absoluten Temperatur $θ$:
- $${N_0}= F \cdot k_{\rm B} \cdot \theta , \hspace{0.3cm}k_{\rm B} = 1.38 \cdot 10^{-23}{ {\rm Ws} }/{ {\rm K} }\hspace{0.2cm}{\rm (Boltzmann-Konstante)}\hspace{0.05cm}.$$
- Bei echt weißem Rauschen würde sich eine unendliche große Leistung ergeben. Deshalb ist stets eine Bandbegrenzung auf $B$ zu berücksichtigen, und es gilt für die wirksame Rauschleistung:
- $$N = \sigma_n^2 = {N_0} \cdot B \hspace{0.05cm}.$$
- Die Amplitude $n$ des Störsignals besitzt eine Gaußsche Wahrscheinlichkeitsdichtefunktion (WDF) mit dem Störeffektivwert $σ_n$:
- $$f_n(n) = \frac{1}{\sqrt{2\pi}\cdot\sigma_n}\cdot {\rm e}^{-{\it n^{\rm 2}}/{(2\sigma_{\it n}^2)}}.$$
- Eigentlich ist beim AWGN–Kanal $H_{\rm K}(f) = 1$ zu setzen. Wir modifizieren dieses Modell für unsere Untersuchungen jedoch in der Form, dass wir eine frequenzunabhängige Dämpfung zulassen:
- $$H_{\rm K}(f) = \alpha_{\rm K}= {\rm const.}$$
- Ein solcher frequenzunabhängiger Dämpfungsfaktor führt nicht zu Verzerrungen.
Untersuchungen beim AWGN–Kanal
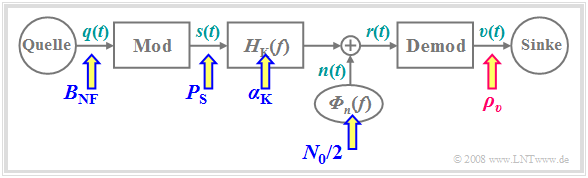
Bei allen Untersuchungen hinsichtlich des Rauschverhaltens gehen wir von folgendem Blockschaltbild aus:
Wir werden dabei stets das Sinken–SNR $ρ_v$ in Abhängigkeit aller Systemparameter berechnen und zu folgenden Ergebnissen kommen:
- Je mehr Sendeleistung $P_{\rm S}$ aufgewendet wird, desto besser ist das Sinken–SNR $ρ_v$. Bei einigen Verfahren ergibt sich sogar ein linearer Zusammenhang.
- Dagegen nimmt $ρ_v$ mit steigender Rauschleistungsdichte $N_0$ monoton ab. Eine Vergrößerung von $N_0$ kann meist durch eine größere Sendeleistung $P_{\rm S}$ ausgeglichen werden.
- Je kleiner der Dämpfungsfaktor $α_{\rm K}$ ist – das heißt, je stärker der Kanal dämpft – um so kleiner wird $ρ_v$. Es besteht oft eine quadratische Abhängigkeit, da die Empfangsleistung $P_{\rm E} = {α_{\rm K}}^2 · P_{\rm S}$ ist.
- Auch ein breitbandigeres Quellensignal (größeres $B_{\rm NF}$) führt zu einem kleineren $ρ_v$, da dadurch auch die HF–Bandbreite vergrößert werden muss und somit mehr Störungen wirksam werden.
Resümee: Unter Berücksichtigung dieser vier Aussagen kommt man zu dem Schluss, dass es Sinn macht, das Sinken–SNR in der Form
- $$\rho_{v } = \rho_{v }(\xi) \hspace{0.5cm} {\rm mit} \hspace{0.5cm}\xi = \frac{ {\alpha_{\rm K} }^2 \cdot P_{\rm S} }{{N_0} \cdot B_{\rm NF} }$$
normiert darzustellen. Die in $ξ$ zusammengefassten Eingangsgrößen sind in obigem Bild mit blauen Pfeilen markiert, während das Qualitätskriterium $ρ_υ$ durch den roten Pfeil hervorgehoben ist.}}
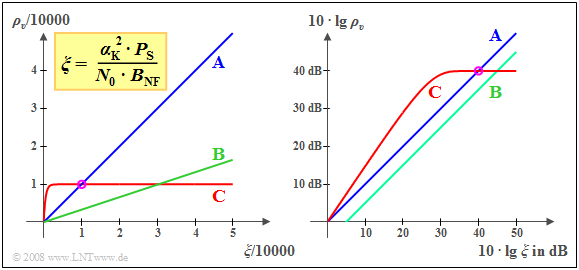
In der linken Grafik ist das Sinken–SNR $ρ_υ$ für drei verschiedene Systeme dargestellt, jeweils in Abhängigkeit von der normierten Leistungskenngröße $$\xi = { {\alpha_{\rm K <div style="clear:both;"> </div> </div>^2 \cdot P_{\rm S}}/({{N_0} \cdot B_{\rm NF}}).$$
Beim System A gilt $ρ_ν = ξ$. Beispielsweise führen die Systemparameter
$$P_{\rm S}= 10 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm}
\alpha_{\rm K} = 10^{-4}\hspace{0.05cm}, \hspace{0.2cm} {N_0} =
10^{-12}{ {\rm W} }/{ {\rm Hz} }\hspace{0.05cm}, \hspace{0.2cm}
B_{\rm NF}= 10\; {\rm kHz}$$
Auch beim System B besteht mit $ρ_υ = ξ/3$ ein linearer Zusammenhang. Anzumerken ist, dass ein Rauschverhalten entsprechend den Systemen A bzw. B bei Zweiseitenband–Amplitudenmodulation mit Modulationsgrad $m → ∞$ bzw. $m$ ≈ 0.5 festzustellen ist (siehe Kapitel 2.2).
Das System C zeigt ein völlig anderes Rauschverhalten. Für kleine Werte von $ξ$ ist dieses System dem System A überlegen, während für $ξ =$ 10000 die Qualität beider Systeme gleich ist. Durch eine Erhöhung von $ξ$ kann das System C im Gegensatz zum System A nicht signifikant verbessert werden.
Ein solches Verhalten ist zum Beispiel bei Digitalsystemen feststellbar, bei denen das Sinken–SNR durch das Quantisierungsrauschen begrenzt wird. Befindet man sich bereits auf dem horizontalen Abschnitt der Kurve, so ist durch eine größere Sendeleistung – und damit verbunden eine kleinere Bitfehlerwahrscheinlichkeit – kein besseres Sinken–SNR zu erzielen.
Meist werden die Größen $ρ_υ$ und $ξ$ in logarithmierter Form dargestellt, wie in der rechten Grafik zu sehen. Durch die doppelt–logarithmische Darstellung ergibt sich für das System A weiterhin die Winkelhalbierende. Die geringere Steigung (Faktor 3) von System B führt nun zu einer Verschiebung um 10 · lg 3 ≈ 5 dB nach unten. Der Schnittpunkt der Systeme A und C verschiebt sich durch die doppelt–logarithmische Transformation von $ξ = ρ_υ =$ 10000 auf 10 · lg $ξ =$ 10 · lg $ρ_υ =$ 40 dB.