Aufgaben:Exercise 4.7: Several Parallel Gaussian Channels

• Return to book

Signal space points in digital modulation

The channel capacity of the AWGN channel with the indicator  $Y = X + N$  was given in the  theory section  as follows
(with the additional unit  "bit"):

$$C_{\rm AWGN}(P_X,\ P_N) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right )\hspace{0.05cm}.$$

The quantities used have the following meaning:

• $P_X$  is the transmission power   ⇒   variance of the random variable  $X$,
• $P_N$  is the noise power   ⇒   variance of the random variable  $N$.

If  $K$  identical Gaussian channels are used in parallel, the total capacity is:

$$C_K(P_X,\ P_N) = K \cdot C_{\rm AWGN}(P_X/K, \ P_N) \hspace{0.05cm}.$$

Here it is considered that

• in each channel the same interference power  $P_N$  is present,
• thus each channel receives the same transmit power  $(P_X/K)$ ,
• the total power is equal to  $P_X$ exactly as in the case  $K = 1$ .

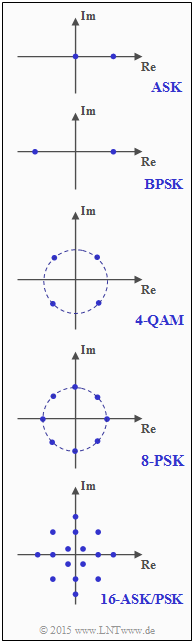
In the adjacent graph, the signal space points for some digital modulation schemes are given:

• Amplitude Shift Keying  (ASK),
• Binary Phase Shift Keying  (BPSK),
• Quadrature Amplitude Modulation  (here:   4-QAM),
• Phase Shift Keying  (here:   8–PSK for GSM Evolution),
• Combined ASK/PSK Modulation  (here:   16-ASK/PSK).

At the beginning of this exercise, check which  $K$–parameter is valid for each method.

Hints:

• The exercise belongs to the chapter  AWGN channel capacity with continuous value input.
• Reference is made in particular to the page  Parallel Gaussian Channels.
• Since the results are to be given in "bit", wird "log₂" is used.

Questions

1

Which parameters   $K$  are valid for the following modulation methods?

$K \ = \ $ $\text{ (ASK)}$

$K \ = \ $ $\text{ (BPSK)}$

$K \ = \ $ $\text{ (4-QAM)}$

$K \ = \ $ $\text{ (8-PSK)}$

$K \ = \ $ $\text{ (16-ASK/PSK)}$

2

What is the channel capacity  $C_K$  for  $K$  equal channels,  each with the noise power  $P_N$  and the transmission power  $P_X(K)$?

	$C_K = K/2 \cdot \log_2 \ \big[1 + P_X/P_N \big]$.
	$C_K = K/2 \cdot \log_2 \ \big[1 + P_X/(K \cdot P_N) \big]$.
	$C_K = 1/2 \cdot \log_2 \ \big[1 + P_X/P_N \big]$.

3

What are the capacities for  $P_X/P_N = 15$?

$K = 1\text{:} \ \ C_K \ = \ $ $\ \rm bit$

$K = 2\text{:} \ \ C_K \ = \ $ $\ \rm bit$

$K = 4\text{:} \ \ C_K \ = \ $ $\ \rm bit$

4

Is there a  (theoretical)  optimum with respect to the number  $K$  of channels?

	Yes:   The largest channel capacity results for  $K = 2$.
	Yes:   The largest channel capacity results for  $K = 4$.
	No:   The larger  $K$, the larger the channel capacity.
	The limit value for  $K \to \infty$  (in bit)  is  $C_K = P_X/P_N/2/\ln (2)$  in  "bit".

Solution

Solution

(1)  The parameter  $K$  is equal to the dimension of the signal space representation:

• For ASK and BPSK,  $\underline{K=1}$.
• For constellations 3 to 5,however,  $\underline{K=2}$  (orthogonal modulation with cosine and sine).

(2)  Correct is the proposed solution 2:

• For each of the channels  $(1 ≤ k ≤ K)$ , the channel capacitance is   $C = 1/2 \cdot \log_2 \ \big[1 + (P_X/K) /P_N) \big]$.  The total capacitance is then larger by a factor of  $K$ :

$$C_K(P_X) = \sum_{k= 1}^K \hspace{0.1cm}C_k = \frac{K}{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{K \cdot P_N} \right )\hspace{0.05cm}.$$

• The proposed solution 1 is too positive. This would apply when limiting the total power to  $K · P_X$ .
• Proposition 3 would imply that no capacity increase is achieved by using multiple independent channels, which is obviously not true.

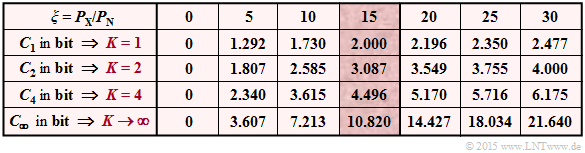
(3)  The table shows the results for  $K = 1$,  $K = 2$  and  $K = 4$  , and various signa–to–noise power ratios  $\xi = P_X/P_N$. For  $\xi = P_X/P_N = 15$  (highlighted column), the result is:

Channel capacity  $C_K$  of  $K$  parallel Gaussian channels for different  $\xi = P_X/P_N$

• $K=1$:   $C_K = 1/2 · \log_2 \ (16)\hspace{0.05cm}\underline{ = 2.000}$ bit,
• $K=2$:   $C_K = 1/2 · \log_2 \ (8.5)\hspace{0.05cm}\underline{ = 3.087}$ bit,
• $K=4$:   $C_K = 1/2 · \log_2 \ (4.75)\hspace{0.05cm}\underline{ = 4.496}$ bit.

(4)  Propositions 3 and 4 are correct, as the following calculations show:

• It is already obvious from the above table that the first proposed solution must be wrong.
• We now write the channel capacity using the natural logarithm and the abbreviation  $\xi = P_X/P_N$:

$$C_{\rm nat}(\xi, K) ={K}/{2} \cdot {\rm ln}\hspace{0.05cm}\left ( 1 + {\xi}/{K} \right )\hspace{0.05cm}.$$

• Then, for large values of  $K$i.e., for small values of the quotient  $\varepsilon =\xi/K$ jholds:

$${\rm ln}\hspace{0.05cm}\left ( 1 + \varepsilon \right )= \varepsilon - \frac{\varepsilon^2}{2} + \frac{\varepsilon^3}{3} - ... \hspace{0.3cm}\Rightarrow \hspace{0.3cm} C_{\rm nat}(\xi, K) = \frac{K}{2} \cdot \left [ \frac{\xi}{K} - \frac{\xi^2}{2K^2} + \frac{\xi^3}{3K^3} - \text{...} \right ]$$

$$\hspace{0.3cm}\Rightarrow \hspace{0.3cm} C_{\rm bit}(\xi, K) = \frac{\xi}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} \cdot \left [ 1 - \frac{\xi}{2K} + \frac{\xi^2}{3K^2} -\frac{\xi^3}{4K^3} + \frac{\xi^4}{5K^4} - \text{...} \right ] \hspace{0.05cm}.$$

• For  $K → ∞$ , the proposed value is:

$$C_{\rm bit}(\xi, K \rightarrow\infty) = \frac{\xi}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} = \frac{P_X/P_N}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} \hspace{0.05cm}.$$

• For smaller values of  $K$  , the result is always a smalle  $C$–value, since

$$\frac{\xi}{2K} > \frac{\xi^2}{3K^2}\hspace{0.05cm}, \hspace{0.5cm} \frac{\xi^3}{4K^3} > \frac{\xi^4}{5K^4} \hspace{0.05cm}, \hspace{0.5cm} {\rm usw.}$$

The last row of the table shows:   With  $K = 4$ one is still far from the theoretical maximum  $($for $K → ∞)$ for large   $\xi$–values.