Difference between revisions of "Information Theory/Further Source Coding Methods"
| Line 212: | Line 212: | ||
==Anwendungsszenario für die Burrows–Wheeler–Transformation== | ==Anwendungsszenario für die Burrows–Wheeler–Transformation== | ||
<br> | <br> | ||
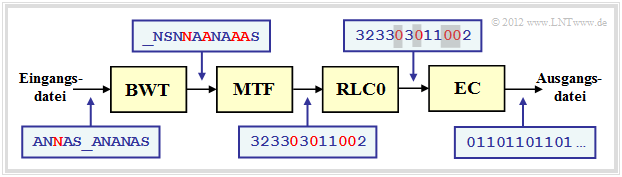
| − | Als Beispiel für die Einbettung der [[Informationstheorie/Weitere_Quellencodierverfahren#Burrows.E2.80.93Wheeler.E2.80.93Transformation|Burrows–Wheeler–Transformation]] (BWT) in eine Kette von Quellencodierverfahren wählen wir eine in [Abel03]<ref>Abel, J.: ''Verlustlose Datenkompression auf Grundlage der Burrows-Wheeler-Transformation''. In: PIK - Praxis der Informationsverarbeitung und Kommunikation, no. 3, vol. 26, S. 140-144, Sept. 2003.</ref> vorgeschlagene Struktur | + | Als Beispiel für die Einbettung der [[Informationstheorie/Weitere_Quellencodierverfahren#Burrows.E2.80.93Wheeler.E2.80.93Transformation|Burrows–Wheeler–Transformation]] (BWT) in eine Kette von Quellencodierverfahren wählen wir eine in [Abel03]<ref>Abel, J.: ''Verlustlose Datenkompression auf Grundlage der Burrows-Wheeler-Transformation''. In: PIK - Praxis der Informationsverarbeitung und Kommunikation, no. 3, vol. 26, S. 140-144, Sept. 2003.</ref> vorgeschlagene Struktur. Wir verwenden dabei das gleiche Textbeispiel $\text{ANNAS_ANANAS}$ wie auf der letzten Seite. Die entsprechenden Strings nach den einzelnen Blöcken sind in der Grafik ebenfalls angegeben. |
[[File:P_ID2477__Inf_T_2_4_S5_neu.png|center|frame|Schema für die Burrows–Wheeler–Datenkompression]] | [[File:P_ID2477__Inf_T_2_4_S5_neu.png|center|frame|Schema für die Burrows–Wheeler–Datenkompression]] | ||
| − | + | *Das '''BWT'''–Ergebnis lautet: $\text{_NSNNAANAAAS}$. An der Textlänge $N = 12$ hat die BWT nichts verändert, doch gibt es jetzt vier Zeichen, die identisch mit ihren Vorgängerzeichen sind (in der Grafik rot hervorgehoben). Im Originaltext war dies nur einmal der Fall. | |
| − | *Das '''BWT'''–Ergebnis lautet: $\text{_NSNNAANAAAS}$. An der Textlänge $N = 12$ hat die BWT nichts verändert, doch gibt es jetzt vier Zeichen, die identisch mit ihren Vorgängerzeichen sind (in der Grafik rot hervorgehoben). Im Originaltext war dies nur einmal der Fall. | + | *Im nächsten Block '''MTF''' (''Move–To–Front'') wird aus jedem Eingangszeichen aus der Menge $\{$ $\rm A$, $\rm N$, $\rm S$, '''_'''$\}$ ein Index $I ∈ \{0, 1, 2, 3\}$. Es handelt sich hierbei aber nicht um ein einfaches Mapping, sondern um einen Algorithmus, der in der [[Aufgabe_2.13Z:_Kombination_BWT_und_''Move-to-Front''|Aufgabe 1.13Z]] angegeben ist. |
| − | *Im nächsten Block '''MTF''' (''Move–To–Front'') wird aus jedem Eingangszeichen aus der Menge $\{$ $\rm A$, $\rm N$, $\rm S$, '''_'''$\}$ ein Index $I ∈ \{0, 1, 2, 3\}$. Es handelt sich hierbei aber nicht um ein einfaches Mapping, sondern um einen Algorithmus, der in der [[Aufgabe_2.13Z:_Kombination_BWT_und_''Move-to-Front''|Aufgabe 1.13Z]] angegeben ist. | + | *Für unser Beispiel lautet die MTF–Ausgangsfolge $323303011002$, ebenfalls mit der Länge $N = 12$. Die vier Nullen in der MTF–Folge (in der Grafik ebenfalls mit roter Schrift) geben an, dass an diesen Stellen das BWT–Zeichen jeweils gleich ist wie sein Vorgänger. |
| − | *Für unser Beispiel lautet die MTF–Ausgangsfolge $323303011002$, ebenfalls mit der Länge $N = 12$. Die vier Nullen in der MTF–Folge (in der Grafik ebenfalls mit roter Schrift) geben an, dass an diesen Stellen das BWT–Zeichen jeweils gleich ist wie sein Vorgänger. | + | *Bei großen ASCII–Dateien kann die Häufigkeit der $0$ durchaus mehr als $50\%$ betragen, während die anderen $255$ Indizes nur selten auftreten. Zur Komprimierung einer solchen Textstruktur eignet sich eine Lauflängencodierung (englisch: ''Run–Length Coding'', RLC) hervorragend. |
| − | *Bei großen ASCII–Dateien kann die Häufigkeit der $0$ durchaus mehr als $50\%$ betragen, während die anderen $255$ Indizes nur selten auftreten. Zur Komprimierung einer solchen Textstruktur eignet sich eine Lauflängencodierung (englisch: ''Run–Length Coding'', RLC) hervorragend. | + | *Der Block '''RLC0''' in obiger Codierungskette bezeichnet eine spezielle [[Informationstheorie/Weitere_Quellencodierverfahren#Laufl.C3.A4ngencodierung_.E2.80.93_Run.E2.80.93Length_Coding|Lauflängencodierung]] für Nullen. Die graue Schattierung der Nullen soll andeuten, dass hier eine lange Nullsequenz durch eine spezifische Bitfolge (kürzer als die Nullsequenz) maskiert wurde. |
| − | *Der Block '''RLC0''' in obiger Codierungskette bezeichnet eine spezielle [[Informationstheorie/Weitere_Quellencodierverfahren#Laufl.C3.A4ngencodierung_.E2.80.93_Run.E2.80.93Length_Coding|Lauflängencodierung]] für Nullen. Die graue Schattierung der Nullen soll andeuten, dass hier eine lange Nullsequenz durch eine spezifische Bitfolge (kürzer als die Nullsequenz) maskiert wurde. | + | *Der Entropiecodierer $($'''EC''', zum Beispiel „Huffman”$)$ sorgt für eine weitere Komprimierung. ''BWT'' und ''MTF'' haben in der Codierungskette nur die Aufgabe, durch eine Zeichenvorverarbeitung die Effizienz von ''RLC0'' und ''EC'' zu steigern. Die Ausgangsdatei ist wieder binär. |
| − | *Der Entropiecodierer ('''EC''', zum Beispiel „Huffman”) sorgt für eine weitere Komprimierung. ''BWT'' und ''MTF'' haben in der Codierungskette nur die Aufgabe, durch eine Zeichenvorverarbeitung die Effizienz von ''RLC0'' und ''EC'' zu steigern. Die Ausgangsdatei ist wieder binär. | ||
Revision as of 15:11, 27 January 2020
Contents
Der Shannon–Fano–Algorithmus
Die Huffman–Codierung aus dem Jahr 1952 ist ein Sonderfall der „Entropiecodierung”. Dabei wird versucht, das Quellensymbol $q_μ$ durch ein Codesymbol $c_μ$ der Länge $L_μ$ darzustellen, wobei die folgende Konstruktionsvorschrift angestrebt wird:
- $$L_{\mu} \approx -{\rm log}_2\hspace{0.15cm}(p_{\mu}) \hspace{0.05cm}.$$
Da $L_μ$ im Gegensatz zu $-{\rm log}_2\hspace{0.15cm}(p_{\mu})$ ganzzahlig ist, gelingt dies nicht immer.
Bereits drei Jahre vor David A. Huffman haben Claude E. Shannon und Robert Fano einen ähnlichen Algorithmus angegeben, nämlich:
- Man ordne die Quellensymbole nach fallenden Auftrittswahrscheinlichkeiten (identisch mit Huffman).
- Man teile die sortierten Zeichen in zwei möglichst gleichwahrscheinliche Gruppen ein.
- Der ersten Gruppe wird das Binärsymbol 1 zugeordnet, der zweiten die 0 (oder umgekehrt).
- Sind in einer Gruppe mehr als ein Zeichen, so ist auf diese der Algorithmus rekursiv anzuwenden.
$\text{Beispiel 1:}$ Wir gehen wie im Einführungsbeispiel für den Huffman–Algorithmus im letzten Kapitel von $M = 6$ Symbolen und folgenden Wahrscheinlichkeiten aus:
- $$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 \hspace{0.05cm}.$$
Dann lautet der Shannon–Fano–Algorithmus:
- $\rm AB$ → 1x (Wahrscheinlichkeit 0.54), $\rm CDEF$ → 0x (Wahrscheinlichkeit 0.46),
- $\underline{\rm A}$ → 11 (Wahrscheinlichkeit 0.30), $\underline{\rm B}$ → 10 (Wahrscheinlichkeit 0.24),
- $\underline{\rm C}$ → 01 (Wahrscheinlichkeit 0.20), $\rm DEF$ → 00x, (Wahrscheinlichkeit 0.26),
- $\underline{\rm D}$ → 001 (Wahrscheinlichkeit 0.12), $\rm EF$ → 000x (Wahrscheinlichkeit 0.14),
- $\underline{\rm E}$ → 0001 (Wahrscheinlichkeit 0.10), $\underline{\rm F}$ → 0000 (Wahrscheinlichkeit 0.04).
Anmerkungen:
- Ein „x” weist wieder darauf hin, dass in nachfolgenden Codierschritten noch Bit hinzugefügt werden müssen.
- Es ergibt sich hier zwar eine andere Zuordnung als bei der Huffman–Codierung, aber genau die gleiche mittlere Codewortlänge:
- $$L_{\rm M} = (0.30\hspace{-0.05cm}+\hspace{-0.05cm} 0.24\hspace{-0.05cm}+ \hspace{-0.05cm}0.20) \hspace{-0.05cm}\cdot\hspace{-0.05cm} 2 + 0.12\hspace{-0.05cm} \cdot \hspace{-0.05cm} 3 + (0.10\hspace{-0.05cm}+\hspace{-0.05cm}0.04) \hspace{-0.05cm}\cdot \hspace{-0.05cm}4 = 2.4\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$
Mit den Wahrscheinlichkeiten entsprechend dem $\text{Beispiel 1}$ führt der Shannon–Fano–Algorithmus zur gleichen mittleren Codewortlänge wie die Huffman–Codierung. Ebenso sind bei vielen (eigentlich: den meisten) anderen Wahrscheinlichkeitsprofilen Huffman und Shannon–Fano aus informationstheoretischer Sicht äquivalent.
Es gibt aber durchaus Fälle, bei denen sich beide Verfahren hinsichtlich der (mittleren) Codewortlänge unterscheiden, wie das folgende Beispiel zeigt.
$\text{Beispiel 2:}$ Wir betrachten $M = 5$ Symbole mit folgenden Wahrscheinlichkeiten:
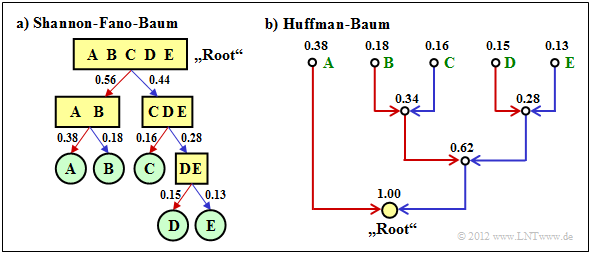
- $$p_{\rm A} = 0.38 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm B}= 0.18 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm C}= 0.16 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D}= 0.15 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm E}= 0.13 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H = 2.19\,{\rm bit/Quellensymbol} \hspace{0.05cm}. $$
Die Grafik zeigt die jeweiligen Codebäume für Shannon–Fano (links) bzw. Huffman (rechts). Die Ergebnisse lassen sich wie folgt zusammenfassen:
- Der Shannon–Fano–Algorithmus führt zum Code $\rm A$ → 11, $\rm B$ → 10, $\rm C$ → 01, $\rm D$ → 001, $\rm E$ → 000 und damit zur mittleren Codewortlänge
- $$L_{\rm M} = (0.38 + 0.18 + 0.16) \cdot 2 + (0.15 + 0.13) \cdot 3 = 2.28\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$
- Mit „Huffman” erhält man $\rm A$ → 1, $\rm B$ → 001, $\rm C$ → 010, $\rm D$ → 001, $\rm E$ → 000 und eine etwas kleinere mittlere Codewortlänge:
- $$L_{\rm M} = 0.38 \cdot 1 + (1-0.38) \cdot 3 = 2.24\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}. $$
- Es gibt keinen Satz von Wahrscheinlichkeiten, bei denen „Shannon–Fano” ein besseres Ergebnis liefert als der Huffman–Algorithmus, der stets den bestmöglichen Entropiecodierer bereitstellt.
- Die Grafik zeigt zudem, dass die Algorithmen im Baumdiagramm in unterschiedlichen Richtungen vorgehen, nämlich einmal von der Wurzel zu den Einzelsymbolen (Shannon–Fano), zum anderen von den Einzelsymbolen zur Wurzel (Huffman).
Arithmetische Codierung
Eine weitere Form der Entropiecodierung ist die arithmetische Codierung. Auch bei dieser müssen die Symbolwahrscheinlichkeiten $p_μ$ bekannt sein. Für den Index gelte weiter $μ = 1$, ... , $M$.
Hier nun ein kurzer Abriss über die Vorgehensweise:
- Im Gegensatz zur Huffman– und zur Shannon–Fano–Codierung wird bei arithmetischer Codierung eine Symbolfolge der Länge $N$ gemeinsam codiert. Wir schreiben abkürzend $Q = 〈\hspace{0.05cm} q_1, q_2$, ... , $q_N \hspace{0.05cm} 〉$.
- Jeder Symbolfolge $Q_i$ wird ein reelles Zahlenintervall $I_i$ zugewiesen, das durch den Beginn $B_i$ und die Intervallbreite ${\it Δ}_i$ gekennzeichnet ist.
- Der „Code” für die Folge $Q_i$ ist die Binärdarstellung eines reellen Zahlenwertes aus diesem Intervall: $r_i ∈ I_i = \big [B_i, B_i + {\it Δ}_i\big)$. Diese Notation besagt, dass zwar $B_i$ zum Intervall $I_i$ gehört (eckige Klammer), aber $B_i + {\it Δ}_i$ gerade nicht mehr (runde Klammer).
- Es gilt stets $0 ≤ r_i < 1$. Sinnvollerweise wählt man $r_i$ aus dem Intervall $I_i$ derart, dass der Wert mit möglichst wenigen Bit darstellbar ist. Es gibt aber stets eine Mindestbitanzahl, die von der Intervallbreite ${\it Δ}_i$ abhängt.
Der Algorithmus zur Bestimmung der Intervallparameter $B_i$ und ${\it Δ}_i$ wird im späteren $\text{Beispiel 4}$ erläutert, ebenso eine Decodiermöglichkeit.
- Zunächst folgt noch ein kurzes Beispiel zur Auswahl der reellen Zahl $r_i$ in Hinblick auf minimale Bitanzahl.
- Genauere Informationen hierzu finden Sie bei der Beschreibung zur Aufgabe 2.11Z.
$\text{Beispiel 3:}$ Für die beiden nachfolgend aufgeführten Parametersätze des arithmetischen Codieralgorithmus ergeben sich folgende reelle Ergebnisse $r_i$ und folgende Codes, die zum zugehörigen Intervall $I_i$ gehören:
- $B_i = 0.25, {\it Δ}_i = 0.10 \ ⇒ \ I_i = \big[0.25, 0.35\big)\text{:}$
- $$r_i = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} = 0.25 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {\rm Code} \hspace{0.15cm} \boldsymbol{\rm 01} \in I_i \hspace{0.05cm},$$
- $B_i = 0.65, {\it Δ}_i = 0.10 \ ⇒ \ I_i = \big[0.65, 0.75\big);$ zu beachten: $0.75$ gehört nicht zum Intervall:
- $$r_i = 1 \cdot 2^{-1} + 0 \cdot 2^{-2} + 1 \cdot 2^{-3} + 1 \cdot 2^{-4} = 0.6875 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {\rm Code} \hspace{0.15cm} \boldsymbol{\rm 1011} \in I_i\hspace{0.05cm}. $$
Um den sequentiellen Ablauf zu organisieren, wählt man allerdings die Bitanzahl konstant zu $N_{\rm Bit} = \big\lceil {\rm log}_2 \hspace{0.15cm} ({1}/{\it \Delta_i})\big\rceil+1\hspace{0.05cm}. $
- Mit der Intervallbreite ${\it Δ}_i = 0.10$ ergibt sich $N_{\rm Bit} = 5$.
- Die tatsächlichen arithmetischen Codes wären also 01000 bzw. 10110.
$\text{Beispiel 4:}$ Nun sei der Symbolumfang $M = 3$ und die Symbole bezeichnen wir mit $\rm X$, $\rm Y$ und $\rm Z$:
- Übertragen werden soll die Zeichenfolge $\rm XXYXZ$ ⇒ Länge der Quellensybolfolge: $N = 5$.
- Auszugehen ist von den Wahrscheinlichkeiten $p_{\rm X} = 0.6$, $p_{\rm Y} = 0.2$ und $p_{\rm Z} = 0.2$.
Die Grafik zeigt den Algorithmus zur Bestimmung der Intervallgrenzen.
- Man unterteilt zunächst den gesamten Wahrscheinlichkeitsbereich $($zwischen $0$ und $1)$ gemäß den Symbolwahrscheinlichkeiten $p_{\rm X}$, $p_{\rm Y}$ und $p_{\rm Z}$ in drei Bereiche mit den Grenzen $B_0$, $C_0$, $D_0$ und $E_0$.
- Das erste zur Codierung anliegende Symbol ist $\rm X$. Deshalb wird im nächsten Schritt der Wahrscheinlichkeitsbereich von $B_1 = B_0 = 0$ bis $E_1 = C_0 = 0.6$ wiederum im Verhältnis $0.6$ : $0.2$ : $0.2$ aufgeteilt.
- Nach dem zweiten Symbol $\rm X$ liegen die Bereichsgrenzen bei $B_2 = 0$, $C_2 = 0.216$, $D_2 = 0.288$ und $E_2 = 0.36$. Da nun das Symbol $\rm Y$ ansteht, erfolgt die Unterteilung des Bereiches zwischen $0.216$ ... $0.288$.
- Nach dem fünften Symbol $\rm Z$ liegt das Intervall $I_i$ für die betrachtete Symbolfolge $Q_i = \rm XXYXZ$ fest. Es muss nun eine reelle Zahl $r_i$ gefunden werden, für die gilt: $0.25056 ≤ r_i < 0.2592$.
- Die einzige reelle Zahl im Intervall $I_i = \big[0.25056, 0.2592\big)$, die man mit sieben Bit darstellen kann, ist $r_i = 1 · 2^{–2} + 1 · 2^{–7} = 0.2578125$. Damit liegt die Coderausgabe fest: 0100001.
Für diese $N = 5$ Symbole werden also sieben Bit benötigt, genau so viele wie bei Huffman–Codierung mit der Zuordnung $\rm X$ → 1, $\rm Y$ → 00, $\rm Z$ → 01.
- Die arithmetische Codierung ist allerdings dann dem Huffman–Code überlegen, wenn die tatsächlich bei Huffman verwendete Bitanzahl noch mehr von der optimalen Verteilung abweicht, zum Beispiel, wenn ein Zeichen extrem häufig vorkommt.
- Oft wird aber einfach nur die Intervallmitte – im Beispiel $0.25488$ – binär dargestellt: 0.01000010011 .... Die Bitanzahl erhält man daraus wie folgt:
- $${\it Δ}_5 = 0.2592 - 0.25056 = 0.00864 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}N_{\rm Bit} = \left\lceil {\rm log}_2 \hspace{0.15cm} \frac{1}{0.00864} \right\rceil + 1\hspace{0.15cm} = \left\lceil {\rm log}_2 \hspace{0.15cm} 115.7 \right\rceil + 1 = 8 \hspace{0.05cm}.$$
- Damit lautet der arithmetische Code für dieses Beispiel mit $N = 5$ Eingangszeichen: 01000010.
- Der Decodiervorgang lässt sich ebenfalls anhand der obigen Grafik erklären. Die ankommende Bitsequenz 0100001 wird zu $r = 0.2578125$ gewandelt.
- Dieser liegt im ersten und zweiten Schritt jeweils im ersten Bereich ⇒ Symbol $\rm X$, im dritten Schritt in zweiten Bereich ⇒ Symbol $\rm Y$, usw.
Weitere Informationen zur Arithmetischen Codierung finden Sie in WIKIPEDIA und in [BCK02][1].
Lauflängencodierung – Run–Length Coding
Wir betrachten eine Binärquelle $(M = 2)$ mit dem Symbolvorrat $\{$ $\rm A$, $\rm B$ $\}$, wobei ein Symbol sehr viel häufiger auftritt als das andere. Beispielsweise sei $p_{\rm A} \gg p_{\rm B}$.
- Eine Entropiecodierung macht hier nur dann Sinn, wenn man diese auf $k$–Tupel anwendet.
- Eine zweite Möglichkeit bietet die Lauflängencodierung (englisch: Run–Length Coding, RLC), die das seltenere Zeichen $\rm B$ als Trennzeichen betrachtet und die Längen $L_i$ der einzelnen Substrings $\rm AA\text{...}A$ als Ergebnis liefert.
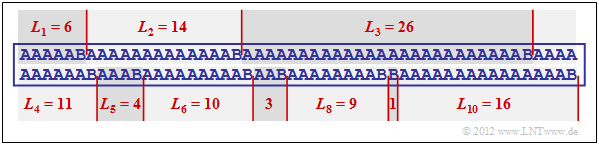
$\text{Beispiel 5:}$ Die Grafik zeigt eine beispielhafte Folge mit den Wahrscheinlichkeiten $p_{\rm A} = 0.9$ und $p_{\rm B} = 0.1$ ⇒ Quellenentropie $H = 0.469$ bit/Quellensymbol.
Die Beispielfolge der Länge $N = 100$ beinhaltet genau zehnmal das Symbol $\rm B$ und neunzigmal das Symbol $\rm A$, das heißt, die relativen Häufigkeiten stimmen hier exakt mit den Wahrscheinlichkeiten überein.
Man erkennt an diesem Beispiel:
- Die Lauflängencodierung dieser Folge ergibt in Dezimalschreibweise die Folge $ \langle \hspace{0.05cm}6, \ 14, \ 26, \ 11, \ 4, \ 10, \ 3,\ 9,\ 1,\ 16 \hspace{0.05cm} \rangle $.
- Stellt man die Längen $L_1$, ... , $L_{10}$ mit jeweils fünf Bit dar, so benötigt man so $5 · 10 = 50$ Bit.
- Die RLC–Datenkomprimierung ist also nicht viel schlechter als der theoretische Grenzwert, der sich entsprechend der Quellenentropie zu $H · N ≈ 47$ Bit ergibt.
- Die direkte Anwendung einer Entropiecodierung hätte hier keine Datenkomprimierung zur Folge; man benötigt weiterhin vielmehr weiterhin $100$ Bit.
- Auch bei der Bildung von Dreiertupeln würde man mit Huffman noch $54$ Bit benötigen, also mehr als mit Run–Length Coding.
Das Beispiel zeigt aber auch zwei Probleme der Lauflängencodierung auf:
- Die Längen $L_i$ der Substrings sind nicht begrenzt. Hier muss man besondere Maßnahmen treffen, wenn eine Länge $L_i$ größer ist als $2^5 = 32$ $($gültig für $N_{\rm Bit} = 5)$, zum Beispiel die Variante Run–Length Limited Coding (RLLC). Siehe auch [Meck09][2] und Aufgabe 2.13.
- Endet die Folge nicht mit $\rm B$ – was bei kleiner Wahrscheinlichkeit $p_{\rm B}$ eher der Normalfall ist, so muss man auch für das Dateiende eine Sonderbehandlung vorsehen.
Burrows–Wheeler–Transformation
Zum Abschluss dieses Quellencodier–Kapitels behandeln wir noch kurz den 1994 von Michael Burrows und David J. Wheeler veröffentlichten Algorithmus [BW94][3],
- der zwar alleine keinerlei Komprimierungspotenzial besitzt,
- aber die Komprimierungsfähigkeit anderer Verfahren stark verbessert.
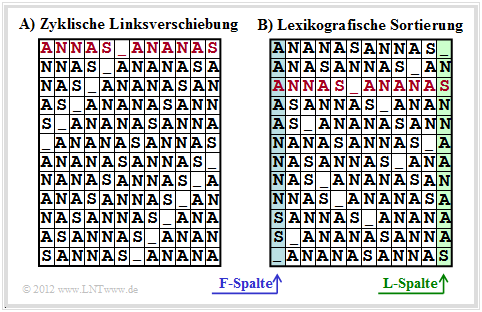
Die Burrows–Wheeler–Transformation bewerkstelligt eine blockweise Sortierung von Daten, die in der Grafik am Beispiel des Textes $\text{ANNAS_ANANAS}$ der Länge $N = 12$ verdeutlicht wird:
- Zunächst wird aus dem String der Länge $N$ eine $N×N$–Matrix erzeugt, wobei sich jede Zeile aus der Vorgängerzeile durch zyklische Linksverschiebung ergibt.
- Danach wird die BWT–Matrix lexikografisch sortiert. Das Ergebnis der Transformation ist die letzte Spalte ⇒ $\text{L–Spalte}$. Im Beispiel ergibt sich $\text{_NSNNAANAAAS}$.
- Des Weiteren muss auch der Primärindex $I$ weitergegeben werden. Dieser gibt die Zeile der sortierten BWT–Matrix an, die den Originaltext enthält (in der Grafik rot markiert).
- Zur Bestimmung von L–Spalte und Primärindex sind natürlich keine Matrixoperationen erforderlich. Vielmehr findet man das BWT–Ergebnis mit Zeigertechnik sehr schnell.
$\text{Außerdem ist zum BWT–Verfahren anzumerken:}$
- Ohne Zusatzmaßnahme ⇒ eine nachgeschaltete „echte Kompression” – führt die BWT zu keiner Datenkomprimierung.
- Vielmehr ergibt sich sogar eine geringfügige Erhöhung der Datenmenge, da außer den $N$ Zeichen nun auch der Primärindex $I$ übermittelt werden muss.
- Bei längeren Texten ist dieser Effekt aber vernachlässigbar. Geht man von 8 Bit–ASCII–Zeichen (jeweils ein Byte) und der Blocklänge $N = 256$ aus, so erhöht sich die Byte–Anzahl pro Block nur von $256$ auf $257$, also lediglich um $0.4\%$.
Wir verweisen auf die ausführlichen Beschreibungen zur BWT in [Abel04][4].
Abschließend soll noch dargestellt werden, wie der Ursprungstext aus der $\text{L–Spalte}$ der BWT–Matrix rekonstruiert werden kann.
- Dazu benötigt man noch den Primärindex $I$, sowie die erste Spalte der BWT–Matrix.
- Diese $\text{F–Spalte}$ (von „First”) muss nicht übertragen werden, sondern ergibt sich aus der $\text{L–Spalte}$ (von „Last”) sehr einfach durch lexikografische Sortierung.
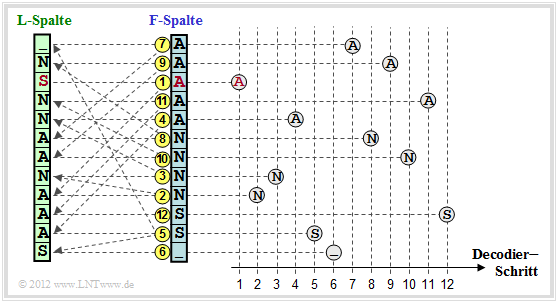
Die Grafik zeigt die Vorgehensweise für das betrachtete Beispiel:
- Man beginnt in der Zeile mit dem Primärindex $I$. Als erstes Zeichen wird das rot markierte $\rm A$ in der $\text{F–Spalte}$ ausgegeben. Dieser Schritt ist in der Grafik mit einer gelben (1) gekennzeichnet.
- Dieses $\rm A$ ist das dritte $\rm A$–Zeichen in der $\text{F–Spalte}$. Man sucht nun das dritte $\rm A$ in der $\text{L–Spalte}$, findet dieses in der mit (2) markierten Zeile und gibt das zugehörige N der $\text{F–Spalte}$ aus.
- Das letzte N der $\text{L–Spalte}$ findet man in der Zeile (3). Ausgegeben wird das Zeichen der F–Spalte in der gleichen Zeile, also wieder ein N.
Nach $N = 12$ Decodierschritten ist die Rekonstruktion abgeschlossen.
$\text{Fazit:}$
- Dieses Beispiel hat gezeigt, dass die Burrows–Wheeler–Transformation nichts anderes ist als ein Sortieralgorithmus für Texte. Das Besondere daran ist, dass die Sortierung eindeutig umkehrbar ist.
- Diese Eigenschaft und zusätzlich seine innere Struktur sind die Grundlage dafür, dass man das BWT–Ergebnis mittels bekannter und effizienter Verfahren wie Huffman (eine Form der Entropiecodierung) und Run–Length Coding komprimieren kann.
Anwendungsszenario für die Burrows–Wheeler–Transformation
Als Beispiel für die Einbettung der Burrows–Wheeler–Transformation (BWT) in eine Kette von Quellencodierverfahren wählen wir eine in [Abel03][5] vorgeschlagene Struktur. Wir verwenden dabei das gleiche Textbeispiel $\text{ANNAS_ANANAS}$ wie auf der letzten Seite. Die entsprechenden Strings nach den einzelnen Blöcken sind in der Grafik ebenfalls angegeben.
- Das BWT–Ergebnis lautet: $\text{_NSNNAANAAAS}$. An der Textlänge $N = 12$ hat die BWT nichts verändert, doch gibt es jetzt vier Zeichen, die identisch mit ihren Vorgängerzeichen sind (in der Grafik rot hervorgehoben). Im Originaltext war dies nur einmal der Fall.
- Im nächsten Block MTF (Move–To–Front) wird aus jedem Eingangszeichen aus der Menge $\{$ $\rm A$, $\rm N$, $\rm S$, _$\}$ ein Index $I ∈ \{0, 1, 2, 3\}$. Es handelt sich hierbei aber nicht um ein einfaches Mapping, sondern um einen Algorithmus, der in der Aufgabe 1.13Z angegeben ist.
- Für unser Beispiel lautet die MTF–Ausgangsfolge $323303011002$, ebenfalls mit der Länge $N = 12$. Die vier Nullen in der MTF–Folge (in der Grafik ebenfalls mit roter Schrift) geben an, dass an diesen Stellen das BWT–Zeichen jeweils gleich ist wie sein Vorgänger.
- Bei großen ASCII–Dateien kann die Häufigkeit der $0$ durchaus mehr als $50\%$ betragen, während die anderen $255$ Indizes nur selten auftreten. Zur Komprimierung einer solchen Textstruktur eignet sich eine Lauflängencodierung (englisch: Run–Length Coding, RLC) hervorragend.
- Der Block RLC0 in obiger Codierungskette bezeichnet eine spezielle Lauflängencodierung für Nullen. Die graue Schattierung der Nullen soll andeuten, dass hier eine lange Nullsequenz durch eine spezifische Bitfolge (kürzer als die Nullsequenz) maskiert wurde.
- Der Entropiecodierer $($EC, zum Beispiel „Huffman”$)$ sorgt für eine weitere Komprimierung. BWT und MTF haben in der Codierungskette nur die Aufgabe, durch eine Zeichenvorverarbeitung die Effizienz von RLC0 und EC zu steigern. Die Ausgangsdatei ist wieder binär.
Aufgaben zum Kapitel
Aufgabe 2.10: Shannon-Fano-Codierung
Aufgabe 2.11: Arithmetische Codierung
Aufgabe 2.11Z: Nochmals Arithmetische Codierung
Aufgabe 2.12: Run–Length Coding & RLLC
Aufgabe 2.13: Burrows-Wheeler-Rücktransformation
Aufgabe 2.13Z: Kombination BWT & „Move-to-Front”
Quellenverzeichnis
- ↑ Bodden, E.; Clasen, M.; Kneis, J.: Algebraische Kodierung. Proseminar, Lehrstuhl für Informatik IV, RWTH Aachen, 2002.
- ↑ Mecking, M.: Information Theory. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2009.
- ↑ Burrows, M.; Wheeler, D.J.: A Block-sorting Lossless Data Compression Algorithm. Technical Report. Digital Equipment Corporation Communications, Palo Alto, 1994.
- ↑ Abel, J.: Grundlagen des Burrows-Wheeler-Kompressionsalgorithmus. In: Informatik Forschung & Entwicklung, no. 2, vol. 18, S. 80-87, Jan. 2004
- ↑ Abel, J.: Verlustlose Datenkompression auf Grundlage der Burrows-Wheeler-Transformation. In: PIK - Praxis der Informationsverarbeitung und Kommunikation, no. 3, vol. 26, S. 140-144, Sept. 2003.