Linear and Time Invariant Systems/Nonlinear Distortions

1. Linear and Time Invariant Systems
2. Signalverzerrungen und Entzerrung
3. Nonlinear Distortions

• Previous page
• Next page

• Previous page
• Next page

Properties of nonlinear systems

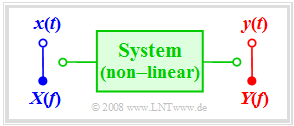
The system description by means of the frequency response  $H(f)$  and/or impulse response  $h(t)$  is only possible for an  LTI System .   However, if the system also contains nonlinear components, as it is assumed for this chapter, no frequency response and no impulse response can be stated, and the model must be designed in a more general way.

Description of a nonlinear systems

Also, in this nonlinear system we denote the signals at the input and output by  $x(t)$  and  $y(t)$  respectively, and the corresponding spectral functions by  $X(f)$  and  $Y(f)$.

An observer will note the following here:

• The transmission characteristics are now also  dependent on the amplitude of the input signal . If  $x(t)$  results in the output signal  $y(t)$, it can now no longer be concluded that the input signal  $K · x(t)$  will always result in the signal  $K · y(t)$ .
• This also implies that the  superposition principle is no longer applicable . Consequently, the result  $x_1(t) + x_2(t)   ⇒   y_1(t) + y_2(t)$  cannot be reasoned from the two correspondences   $x_1(t) ⇒ y_1(t)$  and  $x_2(t) ⇒ y_2(t)$  .
• Due to nonlinearities  new frequencies occur.  If  $x(t)$  is a harmonic oscillation with the frequency  $f_0$, the output signal  $y(t)$  also contains components at multiples of  $f_0$. In communications engineering, these are referred to as  harmonics.
• In practice, an information signal usually contains many frequency components. The harmonics of the low-frequency signal components now fall into the range of higher-frequency useful components.  This results in nonreversible signal falsifications.

Before mentioning   "constellations which result in nonlinear distortions"  at the end of the section the problem of nonlinear distortions is captured mathematically.

• We assume here that  the system has no memory   so that the output value  $y = y(t_0)$  depends only on the instantaneous input value  $x = x(t_0)$ 
• but not on the signal curve  $x(t)$  for  $t < t_0$.

Description of nonlinear systems

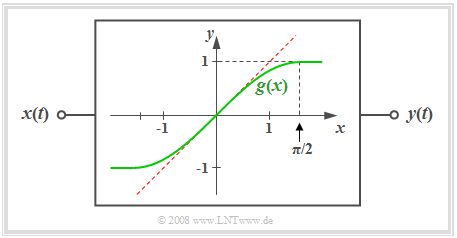
$\text{Definition:}$  A system is said to be  nonlinear if the following relationship exists between the signal value  $x = x(t)$  at the input and the output  $y = y(t)$ : $$y = g(x) \ne {\rm const.} \cdot x.$$ The curve progression  $y = g(x)$  is called the  nonlinear characteristic curve  of the system.

Nonlinear characteristic curve

• In the diagram, as an example, the green curve is the nonlinear characteristic curve  $y = g(x)$  which is shaped according to the first quarter of a sine function.
• The special case of a linear system with the characteristic curve  $y = x$ can be seen dashed in red.

Since every characteristic curve can be developed into a Taylor series around the operating point the output signal can also be represented as follows: $$y(t) = \sum_{i=0}^{\infty}\hspace{0.1cm} c_i \cdot x^{i}(t) = c_0 + c_1 \cdot x(t) + c_2 \cdot x^{2}(t) + c_3 \cdot x^{3}(t) + \hspace{0.05cm}\text{...}$$ If  $x(t)$  has a unit – for exmple "Volt” –, then the coefficients of the Taylor series also have appropriate and different units:

• $c_0$  with  $\rm V$,
• $c_1$  without units,
• $c_2$  with  $\rm 1/V$, etc.

In the above diagram the operating point is identical to the zero point and  $c_0 = 0$ holds.

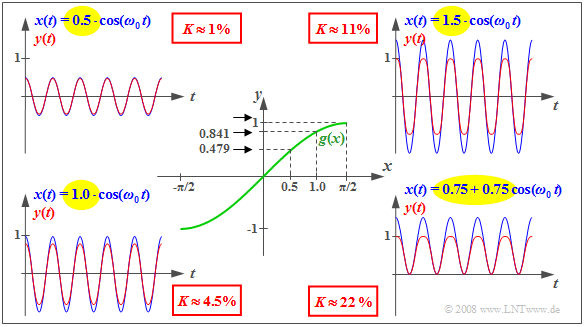
$\text{Example 1:}$  The properties of nonlinear systems listed on the  first page of this section  are illustrated here using the characteristic curve  $y = g(x) = \sin(x)$  shown in the centre of the diagram.

• Here, the direct signal  $x(t) = 0.5$  results in the constant output signal  $y(t) = 0.479$ .
• For  $x(t) = 1$  the input signal results in the output signal  $y(t) = 0.841 ≠ 2 · 0.479$.

• Thus, doubling   $x(t)$  does not cause the doubling of  $y(t)$    ⇒   the superposition principle is violated.

Auswirkungen einer nichtlinearen Kennlinie

The outer diagrams show – each in blue – cosine-shaped input signals  $x(t)$  with different amplitudes  $A$  and the corresponding distorted output signals  $y(t)$ in red. It can be seen that the nonlinear distortions increase with increasing amplitude, which are quantified by the distortion factor  $K$  defined on the next page.

• The diagram on the upper right-hand corner for  $A = 1.5$  clearly shows that  $y(t)$  is no longer cosine-shaped; the half-waves run rounder than the ones of the cosine function.
• But also for  $A = 0.5$  and  $A = 1.0$  the signals  $y(t)$  deviate - although less strongly - from the cosine form due to the harmonics.  That is, new frequency components at multiples of the cosine frequency  $f_0$ arise.

• In the picture on the bottom right-hand corner the characteristic curve is operated unilaterally due to an additional direct component. Now an unbalance in the signal  $y(t)$ can be seen, too.  The lower half-wave is more peaked than the upper one.  The distortion factor here is  $K \approx 22\%$.

The distortion factor

Definition of the distortion factor

To quantitatively capture the non-linear distortions we assume that the input signal  $x(t)$  is cosine-shaped with the amplitude  $A_x$ .

The output signal contains harmonics due to the nonlinear distortions and the following is generally true: $$y(t) = A_0 + A_1 \cdot \cos(\omega_0 t) + A_2 \cdot \cos(2\omega_0 t) + A_3 \cdot \cos(3\omega_0 t) + \hspace{0.05cm}...$$

$\text{Definition:}$  With these amplitude values  $A_i$  the equation for the  distortion factor is:

$$K = \frac {\sqrt{A_2^2+ A_3^2+ A_4^2+ \hspace{0.05cm}\text{...} } }{A_1} = \sqrt{K_2^2+ K_3^2+K_4^2+ \hspace{0.05cm}\text{...} }.$$

In the second equation

• $K_2 = A_2/A_1$  denotes the distortion factor of second order,
• $K_3 = A_3/A_1$  denotes the distortion factor of third order, etc.

Ausdrücklich wird darauf hingewiesen, dass bei der Berechnung des Klirrfaktors die Amplitude  $A_x$  des Eingangssignals nicht berücksichtigt wird. Auch ein entstehender Gleichanteil  $A_0$  bleibt unberücksichtigt.

Im  $\text{Beispiel 1}$  im letzten Abschnitt wurden die Klirrfaktoren mit Werten zwischen etwa  $1\%$  und  $20\%$  angegeben.

• Diese Werte liegen schon deutlich über den Klirrfaktoren preisgünstiger Audioanlagen, für die  $K < 0.1\%$ gilt.
• Bei HiFi–Geräten wird auf die Linearität besonderer Wert gelegt und ein sehr kleiner Klirrfaktor schlägt sich auch im Preis nieder.

Ein Vergleich mit der Seite  Berücksichtigung von Dämpfung und Laufzeit  lässt erkennen, dass für den Sonderfall eines cosinusförmigem Eingangssignals das dort definierte Signal–zu–Verzerrungs–Leistungsverhältnis gleich dem Kehrwert des Klirrfaktors zum Quadrat ist:

$$\rho_{\rm V} = \frac{ \alpha^2 \cdot P_{x}}{P_{\rm V}} = \left(\frac{ A_{1}}{A_x} \right)^2 \cdot \frac{ {1}/{2} \cdot A_{x}^2}{{1}/{2} \cdot (A_{2}^2 + A_{3}^2 + A_{4}^2 + \hspace{0.05cm}...) } = \frac{1}{K^2}\hspace{0.05cm}.$$

Einfluss einer Nichtlinearität auf ein Cosinussignal

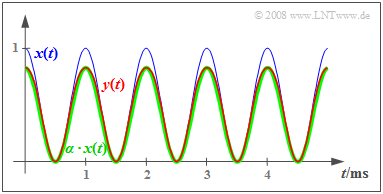
$\text{Example 2:}$  Wir betrachten nun ein mittelwertbehaftetes Cosinussignal:

$$x(t) = {1}/{2} + {1}/{2}\cdot \cos (\omega_0 \cdot t).$$

$x(t)$  nimmt Werte zwischen  $0$  und  $1$  an und ist als blaue Kurve gezeichnet. Die Signalleistung ist

$$P_x = 1/4 + 1/8 = 0.375.$$

Gibt man dieses Signal auf eine Nichtlinearität mit der Kennlinie

$$y=g(x) = \sin(x) \approx x - {x^3}/{6} \hspace{0.05cm},$$

so lautet das Ausgangssignal:

$$y(t) = A_0 + A_1 \cdot \cos (\omega_0 \cdot t)+ A_2 \cdot \cos (2\omega_0 \cdot t)+ A_3 \cdot \cos (3\omega_0 \cdot t)\hspace{0.05cm},$$

$$\Rightarrow \hspace{0.3cm} A_0 = {86}/{192},\hspace{0.3cm}A_1 = {81}/{192},\hspace{0.3cm}A_2 = - {6}/{192},\hspace{0.3cm}A_3 = - {1}/{192}\hspace{0.05cm}.$$

Zur Berechnung der Fourierkoeffizienten wurden die trigonometrischen Umformungen für  $\cos^2(α)$  und  $\cos^3(α)$  verwendet. Der Klirrfaktor ergibt sich damit zu

$$K = \frac {\sqrt{A_2^{\hspace{0.05cm}2} + A_3^{\hspace{0.05cm}2} } }{A_1}\approx 7.5\%\hspace{0.05cm}.$$

Man erkennt weiter, dass das rot skizzierte Signal  $y(t)$  nahezu gleich dem grün gezeichneten Signal  $α · x(t)$  mit  $α = \sin(1) ≈ 5/6$  ist.

Definiert man das Fehlersignal  $ε_1(t) = y(t) - α · x(t)$, so ergibt sich mit dessen Leistung

$$P_{\varepsilon 1} = \frac {(80-86)^2}{192^2} + \frac {6^2 + (-1)^2}{2 \cdot 192^2}\approx 1.48 \cdot 10^{-3}$$

für das Signal–zu–Stör–Leistungsverhältnis:

$$\rho_{{\rm V} 1} = \frac {\alpha^2 \cdot P_x}{P_{\varepsilon 1} } = \frac {(5/6)^2 \cdot 0.375}{1.48 \cdot 10^{-3} }\approx 176 = {1}/{K^2}\hspace{0.05cm}.$$

Dagegen ist das SNR deutlich geringer, wenn man den Dämpfungsfaktor  $α$  nicht berücksichtigt, das heißt, wenn man vom Fehlersignal  $ε_2 = y(t) - x(t)$  ausgeht:

$$P_{\varepsilon 2} = \frac {(86-96)^2}{192^2} + \frac {(81-96)^2 + 6^2 + (-1)^2}{2 \cdot 192^2}\approx 6.3 \cdot 10^{-3} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\rho_{{\rm V} 2} = \frac { P_x}{P_{\varepsilon 2}}= \frac {0.375}{6.3 \cdot 10^{-3}} \approx 60 \hspace{0.05cm}.$$

Clirr measurement

Ein großer Nachteil der Klirrfaktordefinition ist die damit einhergehende Festlegung auf cosinusförmige Testsignale, also auf realitätsferne Bedingungen.

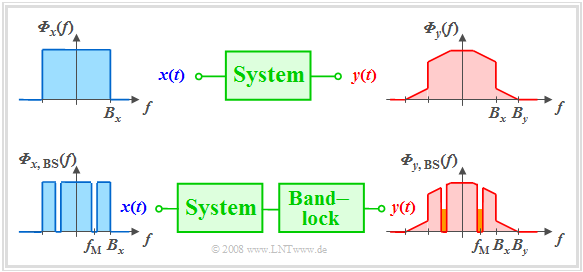
• Bei der so genannten Rauschklirrmessung modelliert man das zu übertragende Signal  $x(t)$  durch weißes Rauschen mit der Rauschleistungsdichte  ${\it \Phi}_x(f)$.
• Zusätzlich bringt man eine schmale Bandsperre  $\rm (BS)$  mit Mittelfrequenz  $f_{\rm M}$  und (sehr kleiner) Bandbreite  $B_{\rm BS}$  in das System ein.

Prinzip der Rauschklirrmessung

Bei einem linearen System wäre das Ausgangsspektrum  ${\it \Phi}_y(f)$  nicht breiter als  $B_x$  und auch im Bereich um  $f_{\rm M}$  gäbe es keine Anteile. 

Diese ergeben sich allein durch Mischprodukte  (Intermodulationsanteile)  verschiedener Spektralanteile, also durch nichtlineare Verzerrungen.

Durch Variation der Mittenfrequenz  $f_{\rm M}$  und Integration über alle diese kleinen Störanteile kann somit die Verzerrungsleistung ermittelt werden. Nähere Angaben zu dieser Methode findet man zum Beispiel in  [Kam04].

Constellations which result in nonlinear distortions

Als Beispiel für das Auftreten nichtlinearer Verzerrungen bei analogen Nachrichtenübertragungssystemen sollen hier einige Konstellationen genannt werden, die zu solchen führen. Inhaltlich bedeutet dies einen Vorgriff auf das Buch  Modulation Methods.

Allgemeines Blockschaltbild eines Nachrichtenübertragungssystems

Nichtlineare Verzerrungen des Sinkensignals  $v(t)$  in Bezug zum Quellensignal  $q(t)$  treten auf, wenn

• es bereits auf dem Kanal – also bezüglich des Sendesignals  $s(t)$  und des Empfangssignals  $r(t)$  – zu nichtlinearen Verzerrungen kommt,
• bei der  Zweiseitenband–Amplitudenmodulation  (ZSB–AM) mit Modulationsgrad  $m > 1$  ein Hüllkurvendemodulator verwendet wird,
• bei ZSB–AM und Hüllkurvendemodulation ein linear verzerrender Kanal vorliegt und zwar auch bei einem Modulationsgrad  $m < 1$,
• man die Kombination Einseitenband–AM und  Hüllkurvendemodulation  verwendet (unabhängig vom Seitenband–zu–Träger–Verhältnis),
• eine  Winkelmodulation  (Oberbegriff für Frequenz– und Phasenmodulation)  angewandt wird und die zur Verfügung stehende Bandbreite nur endlich groß ist.

Exercises for the Chapter

Aufgabe 2.3: Sinusförmige Kennlinie

Aufgabe 2.3Z: Kennlinienbetrieb asymmetrisch

Aufgabe 2.4: Klirrfaktor und Verzerrungsleistung

Aufgabe 2.4Z: Kennlinienvermessung