Classification of the Distortions
Contents
# OVERVIEW OF THE SECOND MAIN CHAPTER #
$\text{Definition:}$ In general, »distortion« is understood to be undesirable deterministic changes in a message signal caused by a transmission system.
In addition to stochastic interferences $($noise, crosstalk, etc.$)$, such deterministic distortions are a critical limitation on the transmission quality and rate for many transmission systems.
This chapter presents these distortions in a summarizing way, in particular:
- The quantitative description of such signal falsifications via the »distortion power«,
- the distinguishing features between »nonlinear and linear distortions«,
- the meaning and computation of the »distortion factor in nonlinear systems«, and
- the effects of »linear attenuation and phase distortions«.
Prerequisites for the second main chapter
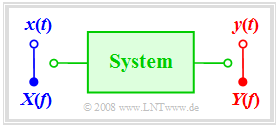
In the following, we consider always a »system«
- whose input is the signal $x(t)$ with the corresponding spectrum $X(f)$, and
- the output signal is denoted by $y(t)$ and its spectrum by $Y(f).$
The block labelled »system« can be a part of an »electrical circuit« or a complete transmission system« consisting of
- »transmitter«,
- »channel«, and
- »receiver«.
For the whole main chapter »Signal Distortions and Equalization« the following shall apply:
- The system be »time-invariant«. If the input signal $x(t)$ results in the output signal $y(t)$, then a later input signal of the same form – in particular $x(t - t_0)$ – will result in the signal $y(t - t_0)$.
- In the following, »no noise« is considered, which is always present in real systems. For the description of these phenomena we refer to the book »Theory of Stochastic Signals«.
- About the system »no detailed knowledge« is assumed. In the following of this chapter, all system properties are derived from the signals $x(t)$ and $y(t)$ or their spectra alone.
- In particular, no specifications are made here with regard to »linearity«. The »system« can be »linear« $($prerequisite for the application of the superposition principle$)$ or »non-linear«.
- Not all system properties are discernible from a single test signal $x(t)$ and its response $y(t)$ . Therefore, sufficiently many test signals must be used for evaluation.
In the following, we will classify transmission systems in more detail in this respect.
Ideal and distortion-free system
$\text{Definition:}$ One deals with an »ideal system« if the output signal $y(t)$ is identical with the input signal $x(t)$:
- $$y(t) \equiv x(t).$$
- It should be noted that such an ideal system does not exist in reality even if statistical disturbances and noise processes $($that always exist but are not considered in this book$)$ are disregarded.
- Every transmission medium exhibits losses $($»attenuation«$)$ and »transit times». Even if these physical phenomena are very small, they are never zero. Therefore it is necessary to introduce a somewhat less strict quality characteristic.
$\text{Definition:}$ A »distortion-free system« exists if the following condition is fulfilled:
- $$y(t) = \alpha \cdot x(t - \tau).$$
- Here, $α$ describes the »attenuation factor« and $τ$ the »transit time«.
- If this condition is not met, the system is said to be » distortive«.
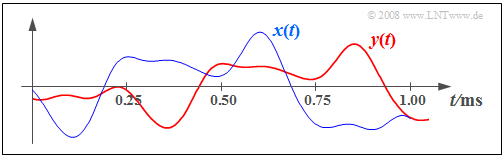
$\text{Example 1:}$ The following diagram shows the input signal $x(t)$ and the output signal $y(t)$ of a nonideal but distortion-free system. The system parameters are $α = 0.8$ and $τ = 0.25 \ \rm ms$.
$\text{Note:}$
- The attenuation factor $α$ can be completely reversed by a receiver-side gain of $1/α = 1.25$, but it must be taken into account that this also increases any noise.
- However, the transit time $τ$ cannot be compensated due to »causality reasons«. It now depends on the application whether such a transit time is subjectively perceived as disturbing or not.
- For example, even with a transit time of one second the $($unidirectional$)$ TV broadcast of an event is still described as "live".
- In contrast to this, transit times of $\text{300 ms}$ are already perceived as very disturbing in bidirectional communication – e.g. a telephone call.
- You either wait for the other person to react or both participants interrupt each other.
Quantitative measure for the signal distortions
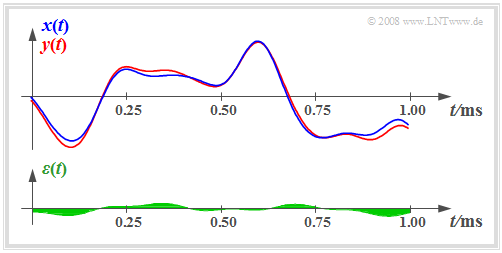
We now consider a distortive system on the basis of the input and output signal.
- We assume that apart from the signal distortions there is no additional frequency-independent attenuation factor $α$ and no additional transit time $τ$. These conditions are fulfilled for the signal sections sketched on the right.
- In addition to the signals $x(t)$ and $y(t)$, the difference signal is shown in the diagram:
- $$\varepsilon(t) = y(t) - x(t).$$
As a quantitative measure of the strength of distortions, the »mean square value of this difference signal« is applicable:
- $$\overline{\varepsilon^2(t)} = \frac{1}{T_{\rm M}} \cdot \int_{ 0 }^{ T_{\rm M}} {\varepsilon^2(t) }\hspace{0.1cm}{\rm d}t\hspace{0.4cm} \left( = P_{\rm V} \right).$$
The following should be noted about this equation:
- The measuring time $T_{\rm M}$ must be chosen sufficiently large. Actually, this equation should be formulated as a limit process.
- This expression is called »mean squared error« $\rm (MSE)$ or »distortion power« $P_{\rm V}$ $($because of "distortion" ⇒ German: "Verzerrung" ⇒ subscript "$\rm V$"$)$.
- If $x(t)$ and $y(t)$ are voltage signals, then $P_{\rm V}$ has the unit of ${\rm V}^2$, meaning the power is related to the resistance $R = 1 \ Ω$ according to the above definition.
$\text{Definition:}$ Making use of the power $P_x$ $($based on $R = 1 \ Ω)$ of the input signal $x(t)$ the »signal–to–distortion (power) ratio« can be given as:
- $$\rho_{\rm V} = \frac{ P_{x} }{P_{\rm V} } \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot \lg \hspace{0.1cm}\rho_{\rm V} = 10 \cdot \lg \hspace{0.1cm}\frac{ P_{x} }{P_{\rm V} }\hspace{0.3cm} \left( {\rm in \hspace{0.15cm} dB} \right).$$
For the signals shown in the diagram above ⇒ $P_x = 4 \ {\rm V}^2$, $P_{\rm V} = 0.04 \ {\rm V}^2$;
- $$10 \cdot {\rm lg} \ ρ_{\rm V} = 20 \ \rm dB.$$
We reference the interactive applet »Linear Distortions of Periodic Signals«.
Elimination of attenuation factor and transit time
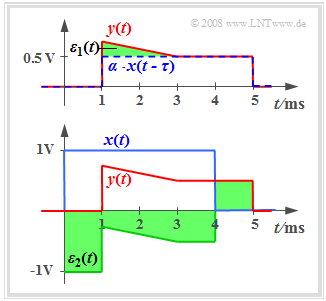
The equations given in the last section do not result in applicable statements if the system is additionally affected by an attenuation factor $α$ and/or a transit time $τ$. The diagram shows the attenuated, delayed and distorted signal
- $$y(t) = \alpha \cdot x(t - \tau) + \varepsilon_1(t).$$
- Here, instead of the »distortion power« the »distortion energy« must be considered because $x(t)$ and $y(t)$ are energy-limited signals.
- The term $ε_1(t)$ summarizes all distortions. It can be seen from the green area that the difference signal ⇒ »error signal« $ε_1(t)$ is relatively small.
In contrast to this, if the attenuation factor $α$ and the transit time $τ$ are unknown, the following should be noted:
- In the second example the difference signal $ε_2(t) = y(t) - x(t)$ determined in this way is relatively large despite small distortions $ε_1(t)$.
- The distortion energy is obtained by varying the unknown quantities $α$ and $τ$ and thus finding the minimum of the »mean squared error«:
- $$E_{\rm V} = \min_{\alpha, \ \tau} \int_{ - \infty }^{ + \infty} {\big[y(t) - \left(\alpha \cdot x(t - \tau) \right) \big]^2}\hspace{0.1cm}{\rm d}t.$$
- The energy of the attenuated and delayed signal $α · x(t - τ)$ is $E_{\rm V} =α^2 · E_x$ independent of the transit time $τ$. Thus for the signal-to-distortion $($energy or power$)$ ratio the following is applicable:
- $$\rho_{\rm V} = \frac{ \alpha^2 \cdot E_{x}}{E_{\rm V}}\hspace{0.3cm}{\rm or}\hspace{0.3cm}\rho_{\rm V}= \frac{ \alpha^2 \cdot P_{x}}{P_{\rm V}} .$$
- The first of these two equations applies to time-limited and thus energy-limited signals, the second one to time-unlimited and thus power-limited signals according to the section »Energy-limited and power-limited signals« in the book »Signal Representation«.
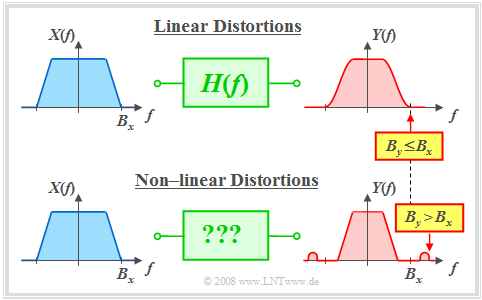
Linear and nonlinear distortions
A distinction is made between »linear distortions« and »nonlinear distortions«:
If the system is linear and time-invariant $(\rm LTI)$, then it is fully characterized by its $\text{frequency response}$ $H(f)$ and the following can be stated:
- According to the $H(f)$ definition the following holds for the output spectrum: $Y(f)=X(f) · H(f)$.
- As a consequence according to the calculation rules of multiplication, $Y(f)$ cannot contain any frequency components that are not already contained in $X(f)$.
- The inverse implies: The output signal $y(t)$ can include any frequency $f_0$ already contained in the input $x(t)$ . The prerequisite is therefore that $X(f_0) ≠ 0$.
- For an LTI system the absolute bandwidth $B_y$ of the output signal is never greater than the bandwidth $B_x$ of the input signal: $B_y \le B_x .$
$\text{Conclusion:}$ The differences between linear and non-linear distortions are illustrated by the following diagram:
$\rm (A)$ In the upper diagram $B_y = B_x$ holds. There are »linear distortions« because in this frequency band $X(f)$ and $Y(f)$ differ.
- A band limitation $(B_y < B_x)$ is a special form of linear distortions, which will be discussed in the »chapter after next«.
$\rm (B)$ The lower diagram shows an example of »non-linear distortions« $(B_y > B_x)$. For such a system no frequency response $H(f)$ can be given.
- Descriptive quantities applicable for nonlinear systems will be explained in the next chapter »Non-linear Distortions« .
In most real transmission channels both linear and nonlinear distortions occur. However, for a whole range of problems the precise separation of the two types of distortions is essential. In [Kam04][1] a corresponding substitute model is shown.
We refer here to the $($German language$)$ learning video »Lineare und nichtlineare Verzerrungen ⇒ »Linear and nonlinear distortions«.
Exercises for the chapter
Exercise 2.1: Linear? Or Non-Linear?
Exercise 2.1Z: Distortion and Equalisation
Exercise 2.2: Distortion Power
Exercise 2.2Z: Distortion Power again
References
- ↑ Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004.