Aufgaben:Exercise 3.10: Mutual Information at the BSC

• Return to book

BSC model considered

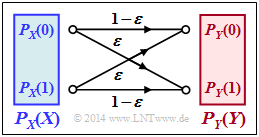
We consider the  Binary Symmetric Channel  $\rm (BSC)$. The parameter values are valid for the whole exercise:

• Crossover probability:   $\varepsilon = 0.1$,
• Probability for  $0$:   $p_0 = 0.2$,
• Probability for  $1$:   $p_1 = 0.8$.

Thus the probability mass function of the source is:   $P_X(X)= (0.2 , \ 0.8)$  and for the source entropy applies:

$$H(X) = p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_0} + p_1\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_1} = H_{\rm bin}(0.2)={ 0.7219\,{\rm bit}} \hspace{0.05cm}.$$

The task is to determine:

• the probability function of the sink:

$$P_Y(Y) = (\hspace{0.05cm}P_Y(0)\hspace{0.05cm}, \ \hspace{0.05cm} P_Y(1)\hspace{0.05cm}) \hspace{0.05cm},$$

• the joint probability function:

$$P_{XY}(X, Y) = \begin{pmatrix} p_{00} & p_{01}\\ p_{10} & p_{11} \end{pmatrix} \hspace{0.05cm},$$

• the mutual information:

$$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \cdot P_{Y}(Y) }\right ] \hspace{0.05cm},$$

• the equivocation:

$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = {\rm E} \hspace{0.02cm} \big [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)} \big ] \hspace{0.05cm},$$

• the irrelevance:

$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = {\rm E} \hspace{0.02cm} \big [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)} \big ] \hspace{0.05cm}.$$

Hints:

• The exercise belongs to the chapter  Application to Digital Signal Transmission.
• Reference is made in particular to the page  Mutual information calculation for the binary channel.
• In  Exercise 3.10Z  the channel capacity  $C_{\rm BSC }$  of the BSC model is calculated.
• This results as the maximum mutual information  $I(X;\ Y)$  by maximization with respect to the probabilities  $p_0$  or  $p_1 = 1 - p_0$.

Questions

1

Calculate the joint probabilities  $P_{ XY }(X, Y)$

$P_{ XY }(0, 0) \ = \ $

$P_{ XY }(0, 1) \ = \ $

$P_{ XY }(1, 0) \ = \ $

$P_{ XY }(1, 1) \ = \ $

2

What is the probability mass function  $P_Y(Y)$  of the sink?

$P_Y(0)\ = \ $

$P_Y(1) \ = \ $

3

What is the value of the mutual information  $I(X;\ Y)$?

$I(X; Y)\ = \ $ $\ \rm bit$

4

Which value results for the equivocation  $H(X|Y)$?

$H(X|Y) \ = \ $ $\ \rm bit$

5

Which statement is true for the sink entropy  $H(Y)$ ?

	$H(Y)$  is never greater than  $H(X)$.
	$H(Y)$  is never smaller than  $H(X)$.

6

Which statement is true for the irrelevance  $H(Y|X)$ ?

	$H(Y|X)$  is never larger than the equivocation  $H(X|Y)$.
	$H(Y|X)$  is never smaller than the equivocation  $H(X|Y)$.

Solution

Solution

(1)  The following applies in general or with the numerical values  $p_0 = 0.2$  and  $\varepsilon = 0.1$ for the quantities sought:

$$P_{XY}(0, 0) = p_0 \cdot (1 - \varepsilon) \hspace{0.15cm} \underline {=0.18} \hspace{0.05cm}, \hspace{0.5cm} P_{XY}(0, 1) = p_0 \cdot \varepsilon \hspace{0.15cm} \underline {=0.02} \hspace{0.05cm},$$

$$P_{XY}(1, 0) = p_1 \cdot \varepsilon \hspace{0.15cm} \underline {=0.08} \hspace{0.05cm}, \hspace{1.55cm} P_{XY}(1, 1) = p_1 \cdot (1 - \varepsilon) \hspace{0.15cm} \underline {=0.72} \hspace{0.05cm}.$$

(2)  In general:

$$P_Y(Y) = \big [ {\rm Pr}( Y = 0)\hspace{0.05cm}, {\rm Pr}( Y = 1) \big ] = \big ( p_0\hspace{0.05cm}, p_1 \big ) \cdot \begin{pmatrix} 1 - \varepsilon & \varepsilon\\ \varepsilon & 1 - \varepsilon \end{pmatrix}.$$

This gives the following numerical values:

$${\rm Pr}( Y = 0)= p_0 \cdot (1 - \varepsilon) + p_1 \cdot \varepsilon = 0.2 \cdot 0.9 + 0.8 \cdot 0.1 \hspace{0.15cm} \underline {=0.26} \hspace{0.05cm},$$

$${\rm Pr}( Y = 1)= p_0 \cdot \varepsilon + p_1 \cdot (1 - \varepsilon) = 0.2 \cdot 0.1 + 0.8 \cdot 0.9 \hspace{0.15cm} \underline {=0.74} \hspace{0.05cm}.$$

(3)  For the mutual information, according to the definition with  $p_0 = 0.2$,  $p_1 = 0.8$  and  $\varepsilon = 0.1$:

$$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \hspace{-0.05cm}\cdot \hspace{-0.05cm} P_{Y}(Y) }\right ] \hspace{0.3cm} \Rightarrow$$

$$I(X;Y) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.18}{0.2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.26} + 0.02 \cdot {\rm log}_2 \hspace{0.08cm} \frac{0.02}{0.2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.74} + 0.08 \cdot {\rm log}_2 \hspace{0.08cm} \frac{0.08}{0.8 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.26} + 0.72 \cdot {\rm log}_2 \hspace{0.08cm} \frac{0.72}{0.8 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.74} \hspace{0.15cm} \underline {=0.3578\,{\rm bit}} \hspace{0.05cm}.$$

(4)  With the source entropy  $H(X)$  given, we obtain for the equivocation:

$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = H(X) - I(X;Y) = 0.7219 - 0.3578 \hspace{0.15cm} \underline {=0.3642\,{\rm bit}} \hspace{0.05cm}.$$

• However, one could also apply the general definition with the inference probabilities  $P_{X|Y}(⋅)$ :

$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = {\rm E} \hspace{0.02cm} \left [ \hspace{0.05cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)} \hspace{0.05cm}\right ] = {\rm E} \hspace{0.02cm} \left [ \hspace{0.05cm} {\rm log}_2 \hspace{0.1cm} \frac{P_Y(Y)}{P_{XY} (X, Y)} \hspace{0.05cm} \right ] \hspace{0.05cm}$$

• In the example, the same result  $H(X|Y) = 0.3642 \ \rm bit$  is also obtained according to this calculation rule:

$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.26}{0.18} + 0.02 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.74}{0.02} + 0.08 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.26}{0.08} + 0.72 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.74}{0.72} \hspace{0.05cm}.$$

(5)  Correct is the proposed solution 2:

• In the case of disturbed transmission  $(ε > 0)$  the uncertainty regarding the sink is always greater than the uncertainty regarding the source.  One obtains here as a numerical value:

$$H(Y) = H_{\rm bin}(0.26)={ 0.8268\,{\rm bit}} \hspace{0.05cm}.$$

• With error-free transmission  $(ε = 0)$,  on the other hand,  $P_Y(⋅) = P_X(⋅)$  and  $H(Y) = H(X)$  would apply.

(6)  Here, too, the second proposed solution is correct:

• Because of  $I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)$ ,  $H(Y|X)$  is greater than  $H(X|Y)$ by the same magnitude that  $H(Y)$  is greater than  $H(X)$:

$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(Y) -I(X;Y) = 0.8268 - 0.3578 ={ 0.469\,{\rm bit}} \hspace{0.05cm}$$

• Direct calculation gives the same result  $H(Y|X) = 0.469\ \rm bit$:

$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = {\rm E} \hspace{0.02cm} \left [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)} \right ] = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9} + 0.02 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.08 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.72 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9} \hspace{0.05cm}.$$